06. 고객 행동 예측 (1) - 클러스터링 개념
9) 데이터 로드
현재 알고있는 데이터들은 다음과 같습니다.
- use_log.csv : 스포츠 센터의 이용 이력 데이터. 기간은 2018년 4월 ~ 2019년 3월
- customer_master.csv : 2019년 3월 말의 회원 데이터
- class_master.csv : 회원 구분 데이터(종일, 주간, 야간)
- campaign_master.csv : 캠페인 구분 데이터(입회비 무료 등)
- customer_join.csv : 앞서 탐색적 데이터 분석에서 작성한 이용 이력을 포함한 고객 데이터
uselog 데이터와 customer 데이터를 로드해둡니다.
import pandas as pd
uselog = pd.read_csv('use_log.csv')
customer = pd.read_csv('customer_join.csv')이제 고객 데이터를 그룹화해봅시다. 여기서는 탈퇴 여부로 분류하는 것이 아니라, 이용 이력을 이용해서 그룹화합니다. 이 경우 미리 정해진 정답이 없기 때문에 비지도 학습 클러스터링을 이용합니다.
10) 클러스터링 알고리즘 : K-means
▶[코드스니펫] 참고자료) K-Means
https://youtu.be/9TR54u08IGU(1) 지도 학습과 비지도 학습
앞서 배운 영화 장르 분류 문제와 같은 분류(Classification) 문제를 상기해봅시다. 학습 시에는 훈련 데이터의 X 데이터인 X_train이 있었고, 이에 대한 정답지인 y_train이 존재해왔습니다. 이렇게 X 데이터와 y 데이터를 가지고 학습하는 학습 방법을 지도 학습(Supervised Learning)이라고 합니다.
반면, 학습할 때, y 데이터가 없는 상태로 X 데이터로부터 패턴과 구조를 발견하는 학습 방법을 비지도 학습(Unsupervised Learning)이라고 합니다. 클러스터링(Clustering)은 대표적인 비지도 학습 방법입니다. 한국어로는 군집화 내지는 군집이라고 부릅니다
클러스터링(Clustering)은 레이블을 모르더라도 비슷한 속성을 가진 데이터들끼리 묶어주는 군집하는 알고리즘입니다. 대표적인 알고리즘으로 K-means가 존재합니다. 분류 문제도 나이브 베이즈 분류기나 결정 트리 등 다양한 알고리즘이 있듯이, 클러스터링에도 K-means 외에도 다양한 알고리즘이 있습니다.
(2) K가 의미하는 것
K-means 알고리즘에서 K는 묶을 그룹(클러스터)의 개수를 의미하고 means는 평균을 의미합니다. 단어 그대로의 의미를 해석해보면 각 군집의 평균(mean)을 활용하여 K개의 군집으로 묶는다는 의미로, 여기서 평균이란 각 클러스터의 중심과 데이터들의 평균 거리를 의미하는데 자세히는 뒤에서 살펴봅시다.
아래의 그림은 어떤 데이터들을 시각화 해본 것입니다.
여러분들에게 서로 유사한 데이터들을 하나의 그룹으로 묶는 방식으로 3개의 그룹으로 한 번 나누어보라고 한다면 여러분들은 어떻게 이 데이터들을 나누실건가요?
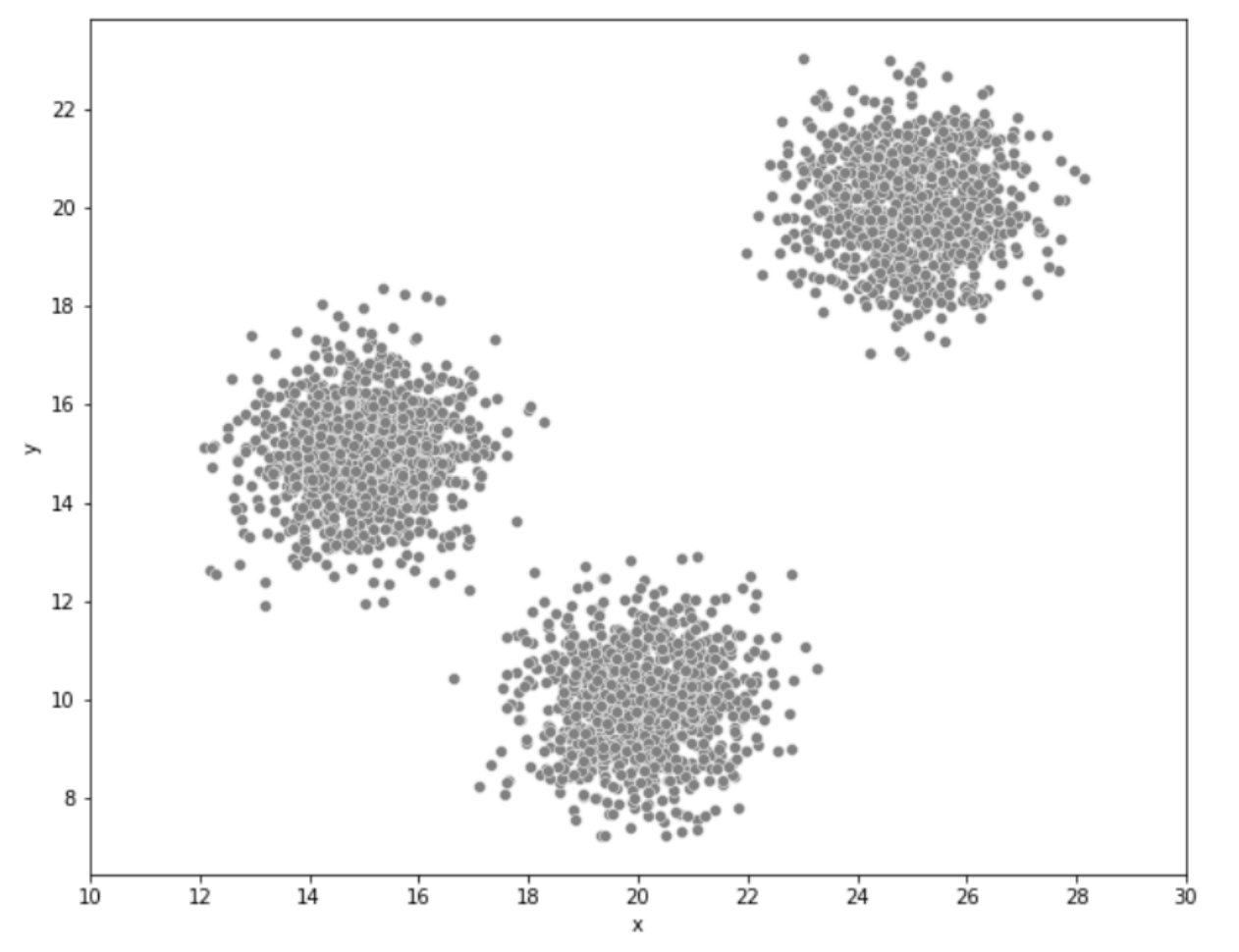
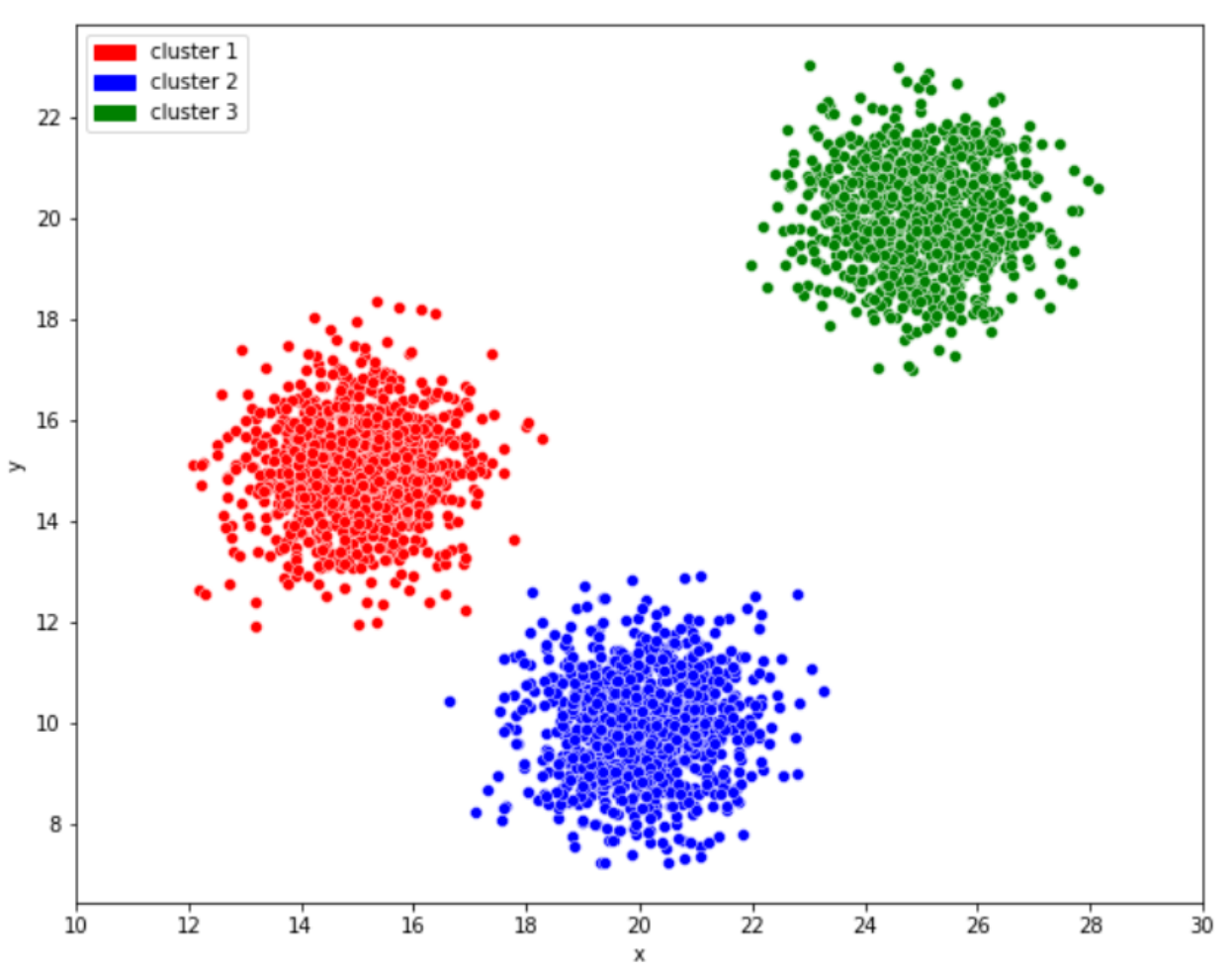
대부분의 분들이라면 아래의 그림과 같이 3개의 그룹으로 나눌 거에요.
이는 K-means 알고리즘에서 K가 3인 경우에 속합니다.
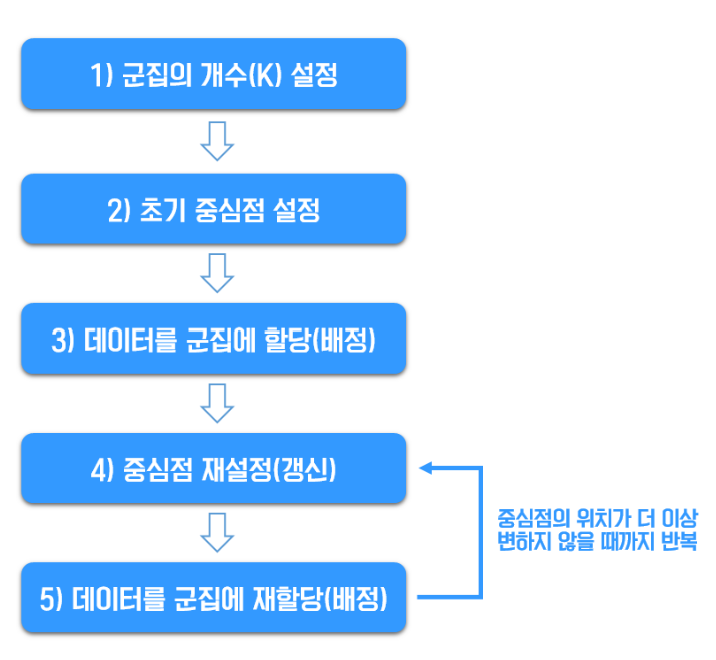
(3) K-means의 동작 순서
K-means 알고리즘의 작동 원리는 다음과 같이 5가지 단계로 구성됩니다.
K-means 알고리즘으로 군집화하는 5가지 단계의 과정을 하나씩 살펴볼게요.
가. 군집의 개수(K) 설정
군집의 개수는 여러분들이 결정하는 거에요. 여러분들이 이 데이터를 몇 개의 그룹까지 나눠봐라고 K-means에게 요구를 하는 거에요
니. 초기 중심점 설정
중심점은 영어로 'Centroid'라고 표현하며 이는 무게중심을 뜻합니다. 초기 중심점으로 어떤 값을 선택하는가에 따라 성능이 크게 달라지는 성질을 가지고 있는데요. 따라서 초기 중심 값을 잘 설정해야하며 다음과 같은 몇가지 방법들이 있습니다.
1) Randomly select (랜덤으로 정하기)
2) Manually assign (사람이 수동으로 정하기)
3) K-means++ (알고리즘으로 정하기
▶ [코드스니펫] 참고자료) K-Means ++
https://ko.wikipedia.org/wiki/K-%ED%8F%89%EA%B7%A0_%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98#k-%ED%8F%89%EA%B7%A0++(다) 데이터를 군집에 할당(배정)하기
그 다음 거리 상 가장 가까운 군집(중심점)으로 주어진 모든 데이터를 할당 또는 배정합니다.
(라) 중심점 재설정(갱신)하기
모든 주어진 데이터의 군집 배정이 끝나면 군집의 중심점(Centroid)을 그 군집의 속하는 데이터들의 가장 중간(평균)에 위치한 지점으로 재설정합니다.
(마) 데이터를 군집에 재할당(배정)하기
3)에서 했던 방법과 똑같이 시행 후, 중심점이 바뀌지 않을 때까지 4)와 5)를 반복합니다.
▼ 4) K-means 그림으로 이해하기
- 4) K-means 그림으로 이해하기 다음과 같이 6개의 데이터가 주어졌다고 하자. 이 주어진 데이터를 K-means 알고리즘의 작동 과정에 따라 군집화 해보자.
step 1) 군집의 개수(K) 설정하기
군집의 개수는 K는 임의대로 3으로 설정하기로 하자.step 2) 초기 중심점 설정하기
여러가지 설정 방법이 있지만 여기서는 편의상 초기 중심점(Centroid) c1, c2, c3는 다음과 같이 랜덤으로 설정한다.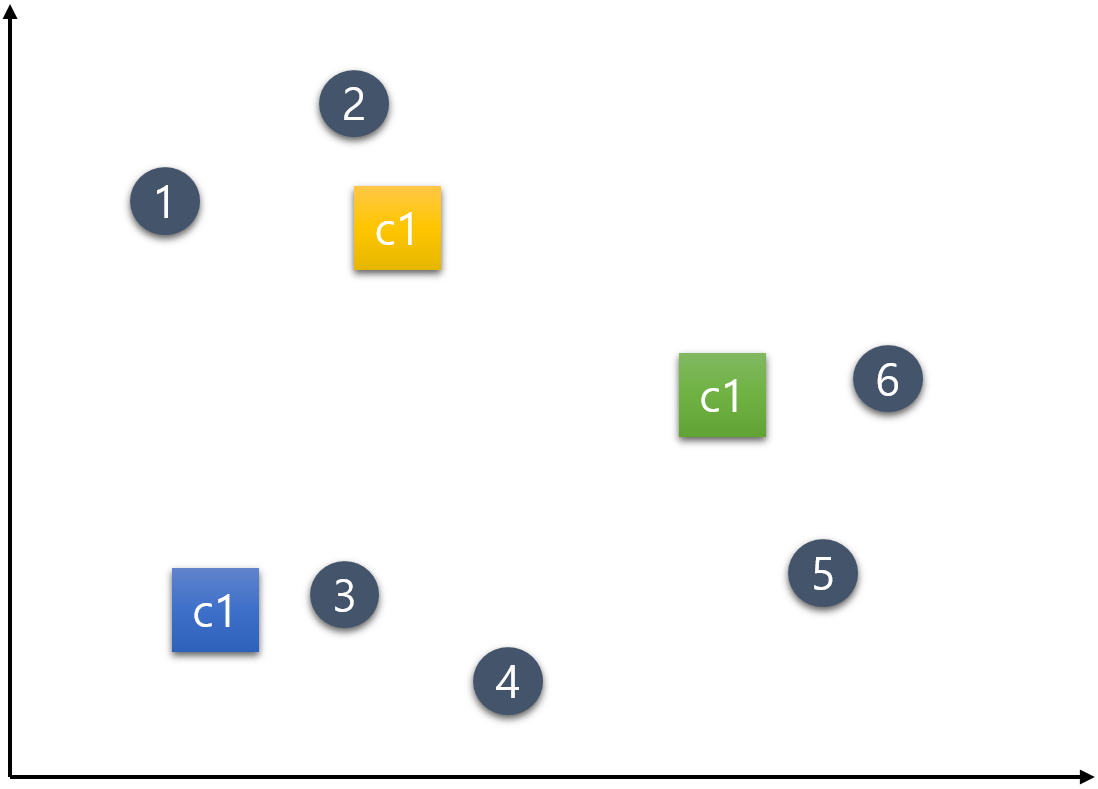
step 3) 데이터를 군집에 할당(배정)하기
거리 상 가장 가까운 군집(중심점)으로 주어진 데이터를 할당 또는 1번 데이터부터 시작해서 6번 데이터까지 각각의 중심점에 가까운 군집으로 배정한다.1번 데이터.
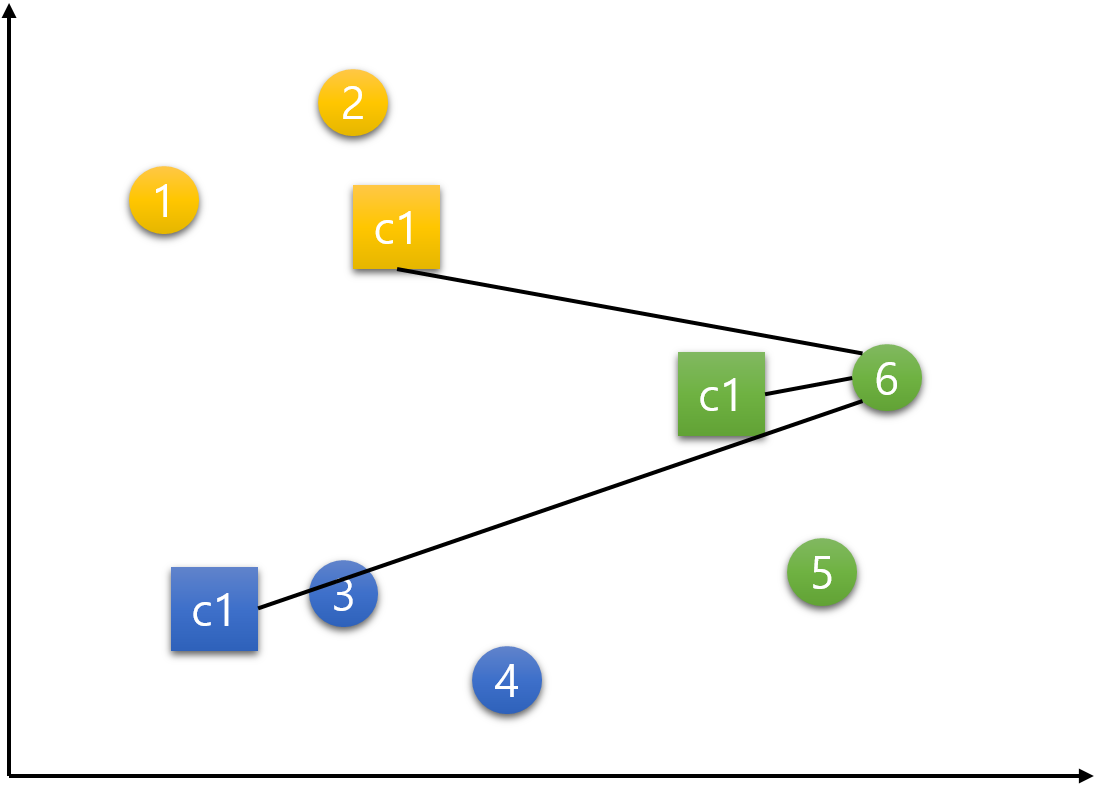
아래의 그림과 같이 c1, c2, c3 중심점으로부터 거리를 측정한다.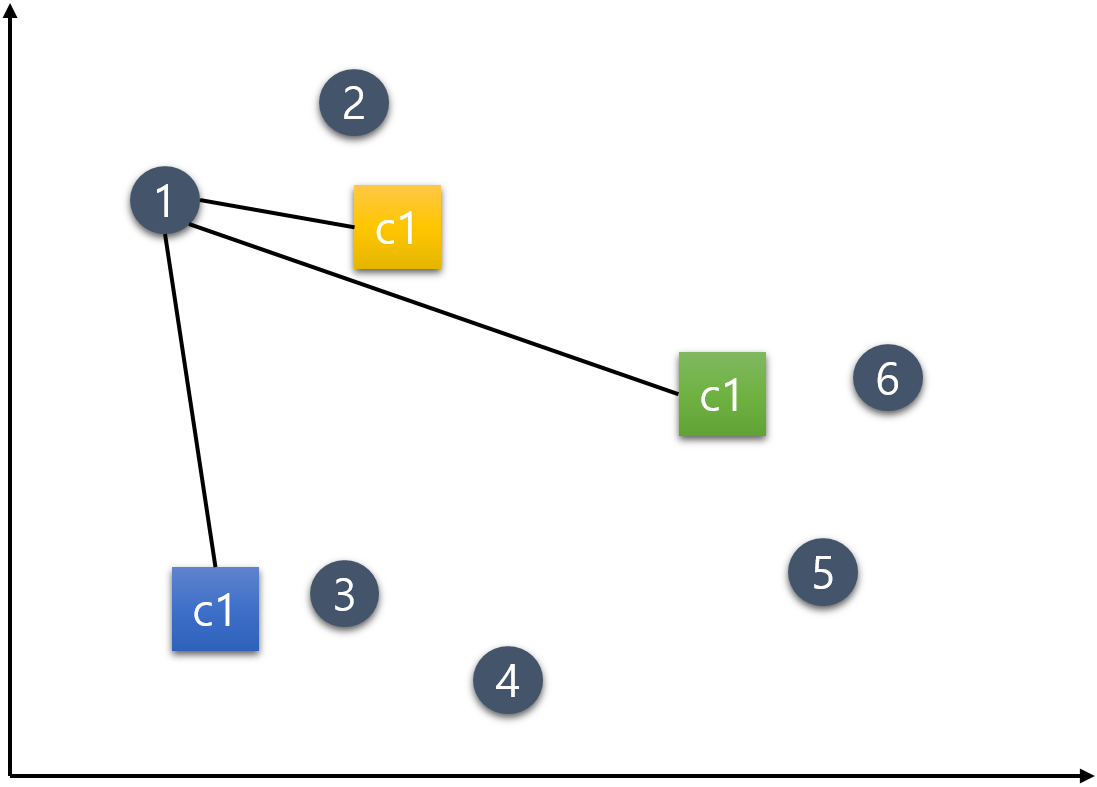
가장 가까이 위치하는 중심점의 군집으로 배정한다. 1번 데이터의 경우 c1 중심점과 가장 가까우므로 노란색으로 바뀐다. 
1번 외 나머지 데이터들도 같은 방식으로 배정한다.2번 데이터.
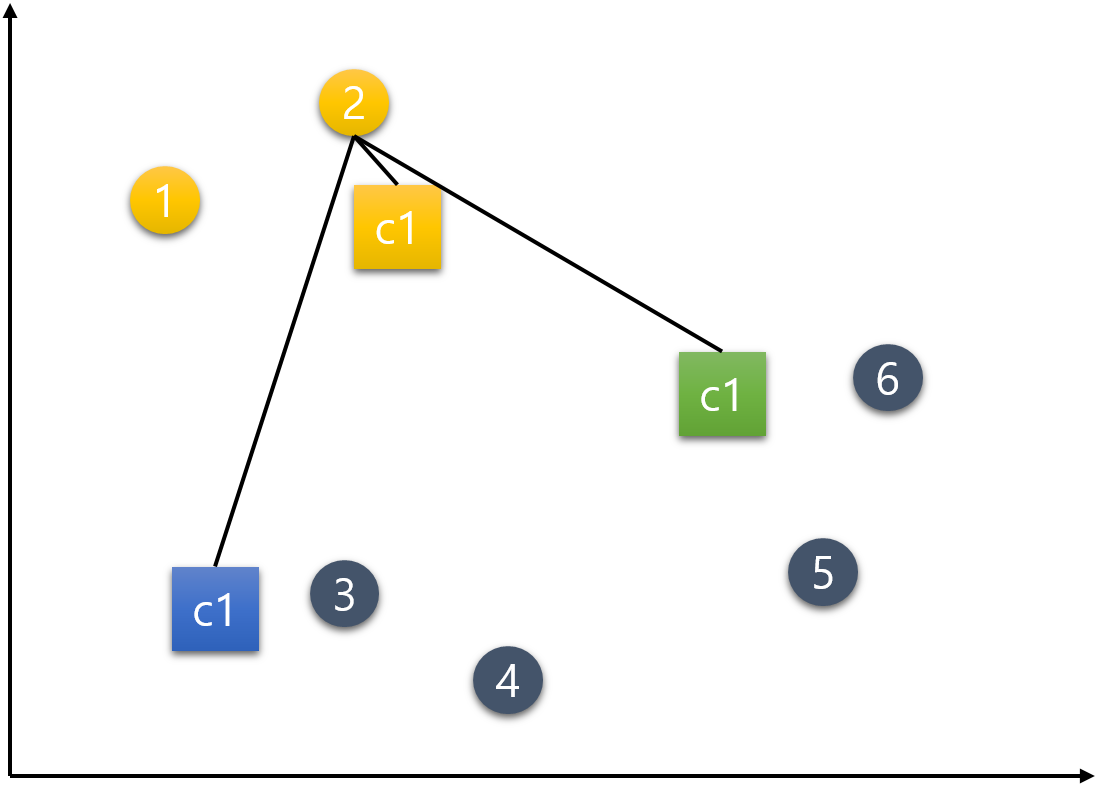
3번 데이터.
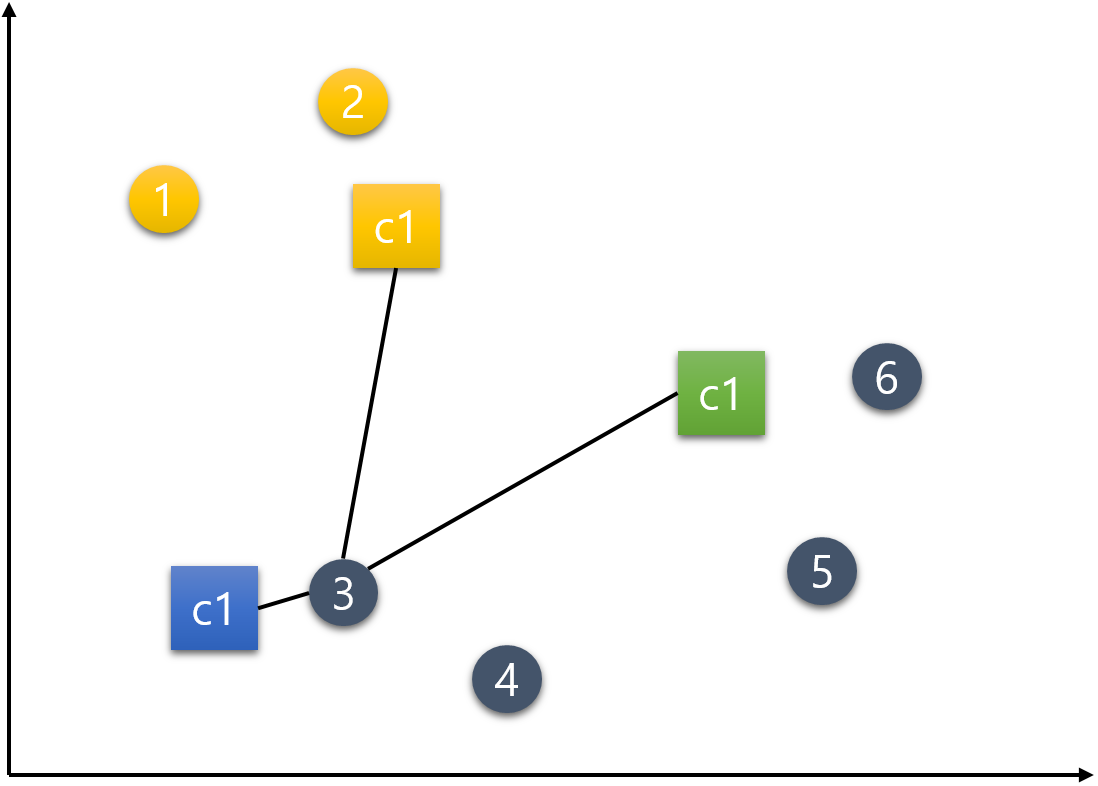
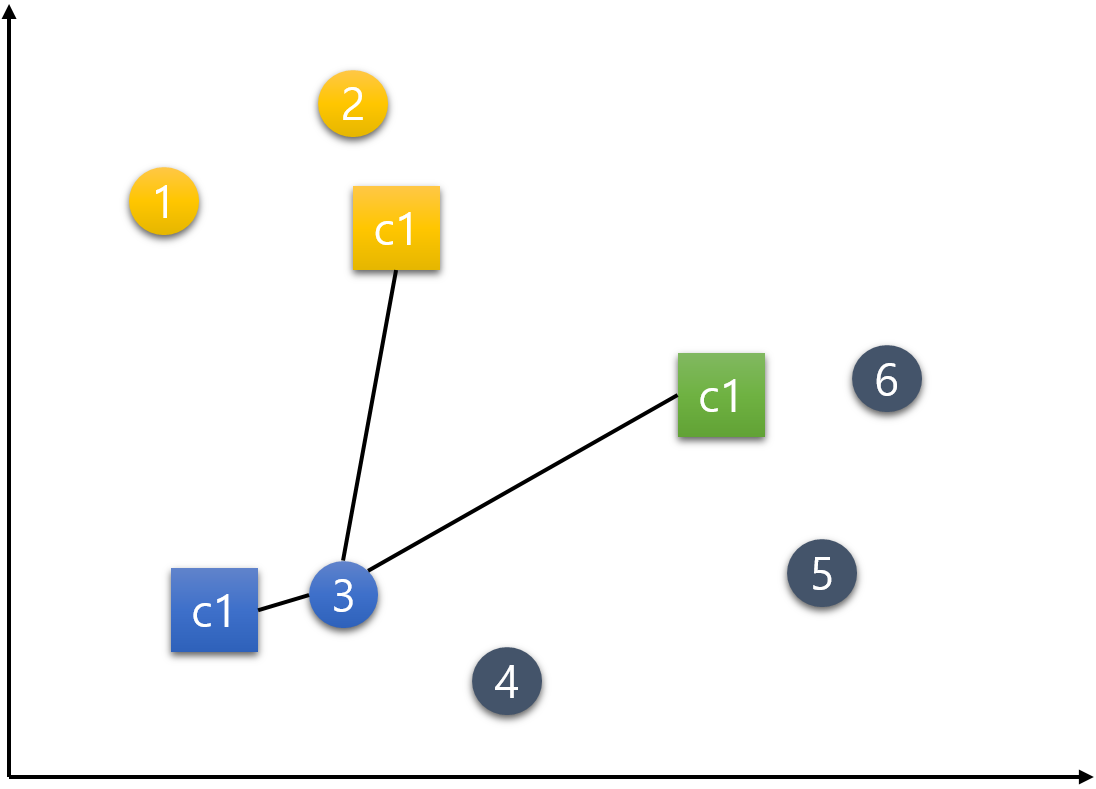
4번 데이터.
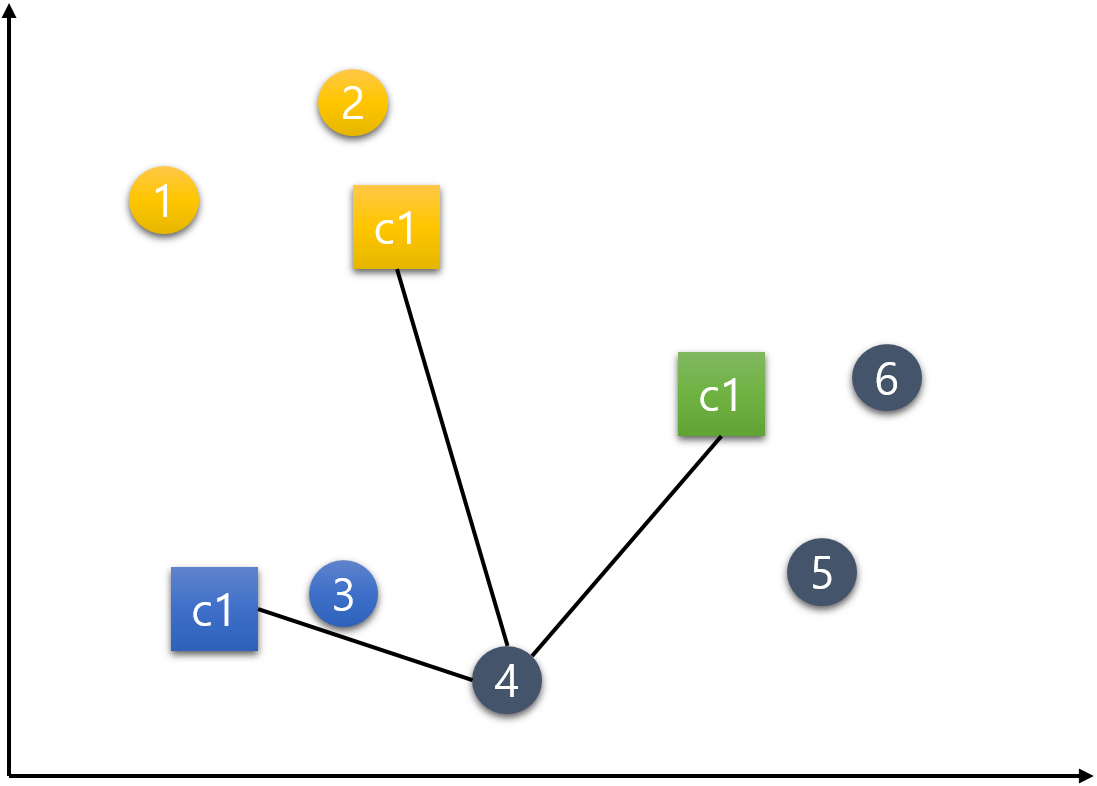
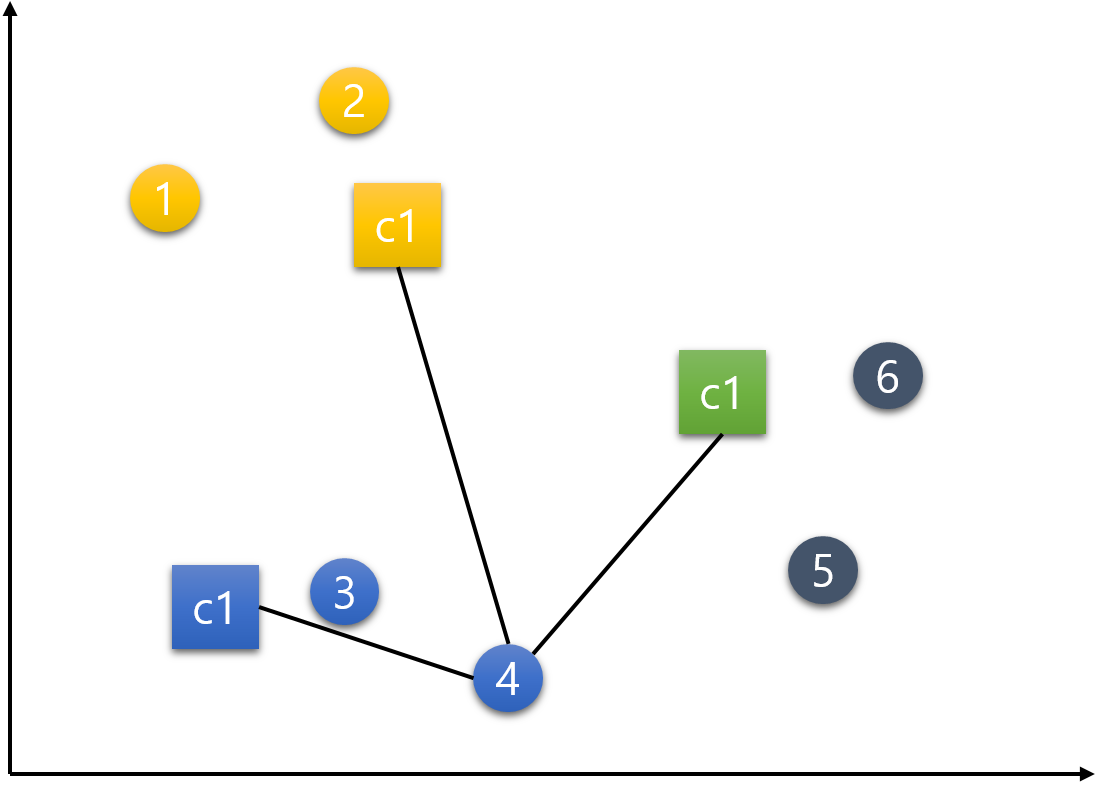
5번 데이터.
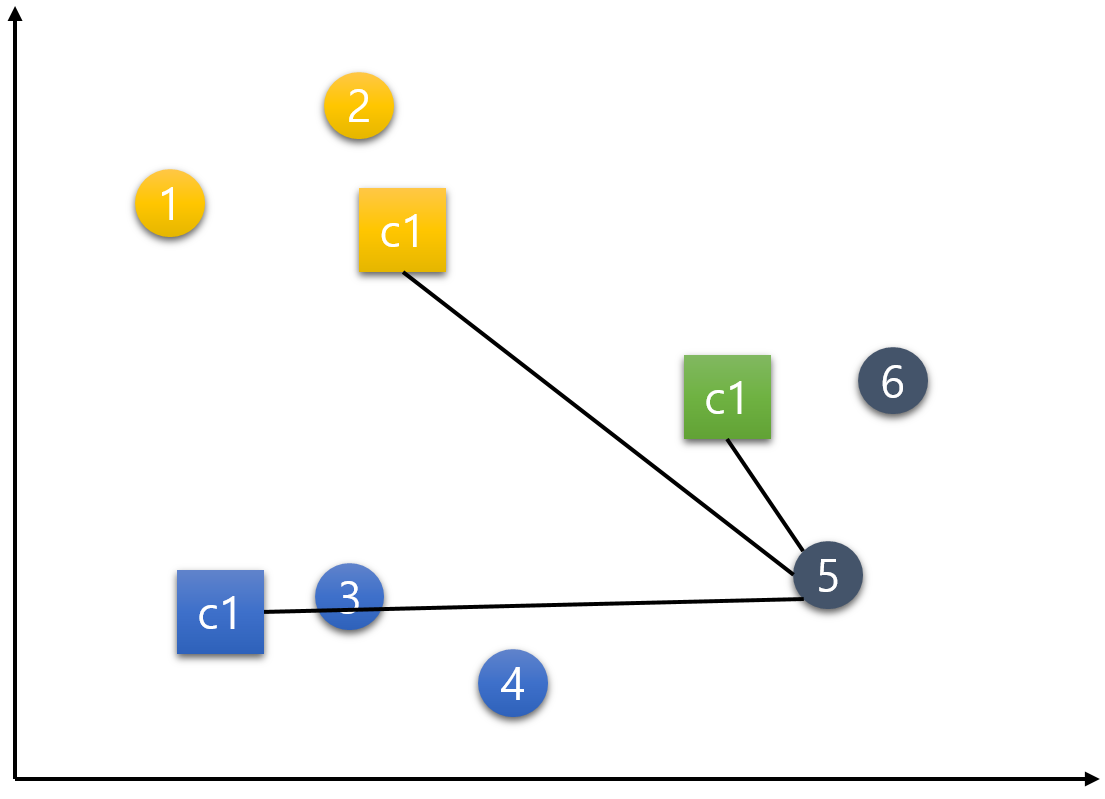
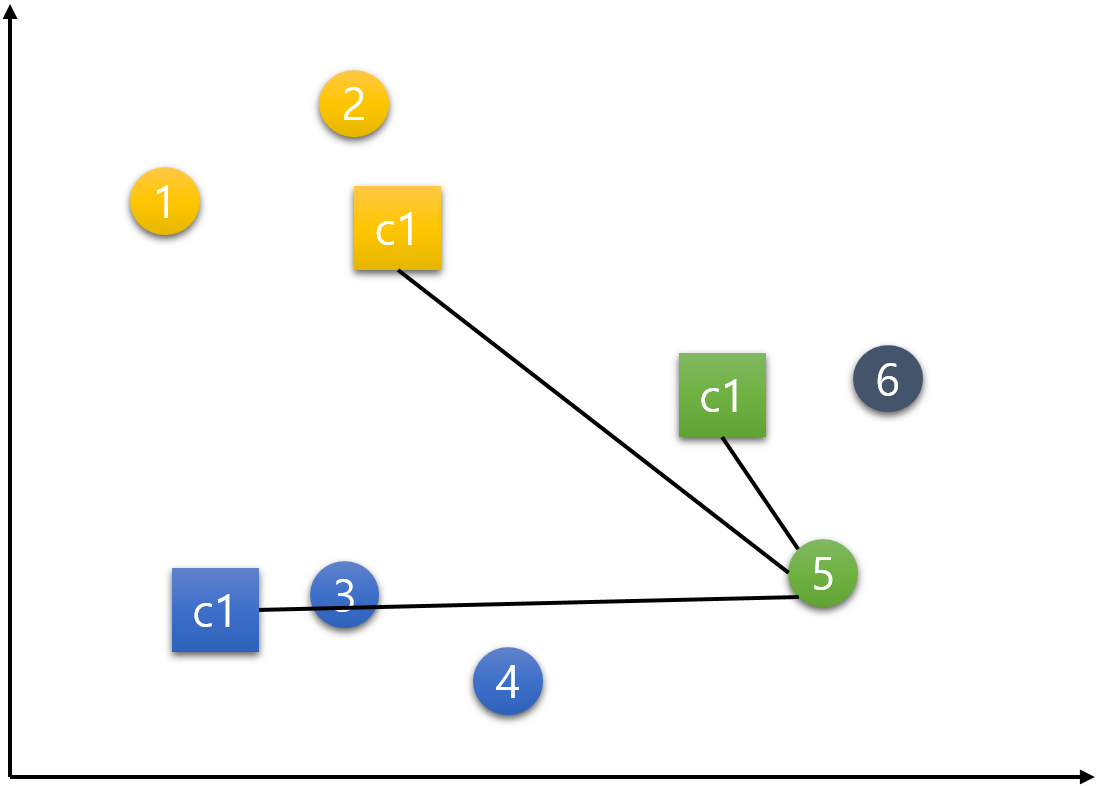
6번 데이터.
이제 모든 데이터들이 한 번씩 각각의 군집들로 배정이 되었다.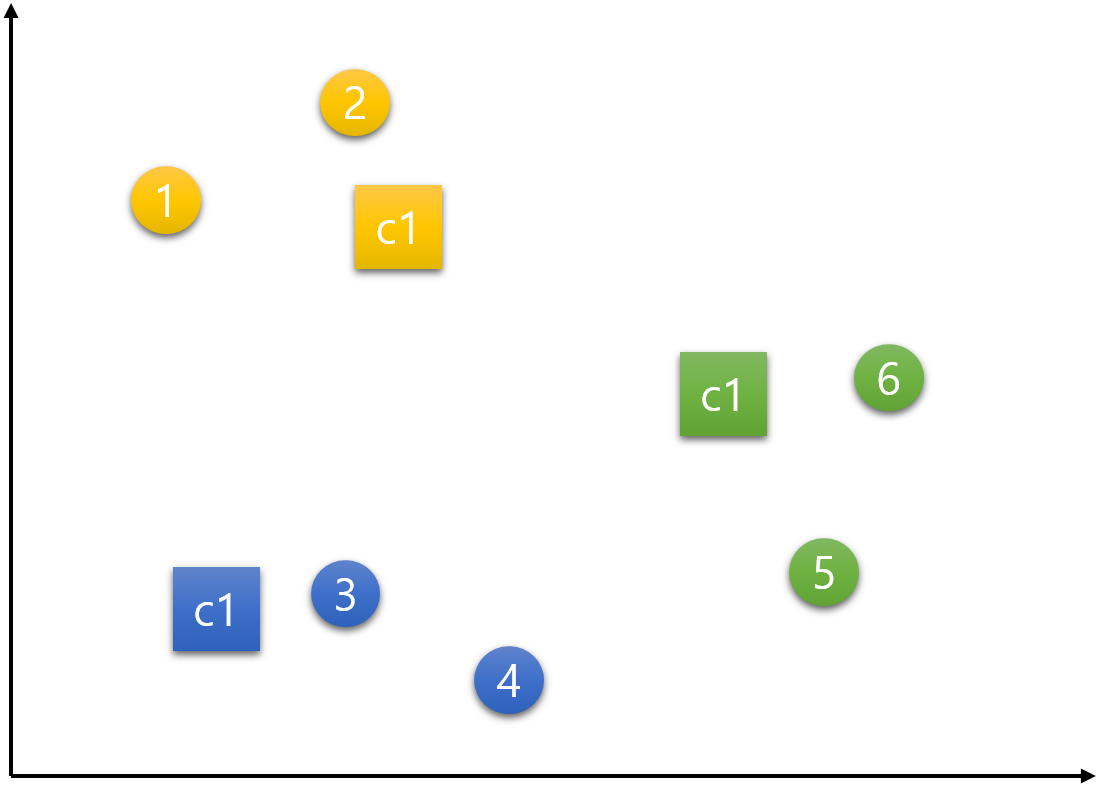 
step 4) 중심점 재설정(갱신)하기
이제 중심점을 재설정하는 단계이다. 노랑, 파랑, 초록 각각의 중심점은 그 군집의 속하는 데이터들의 가장 중간(평균)에 위치한 지점으로 재설정한다. 중심점 노랑은 데이터 1, 2의 평균인 지점으로, 중심점 파랑은 데이터 3, 4의 평균인 지점으로, 중심점 초록은 데이터 5, 6의 평균인 지점으로 갱신된다.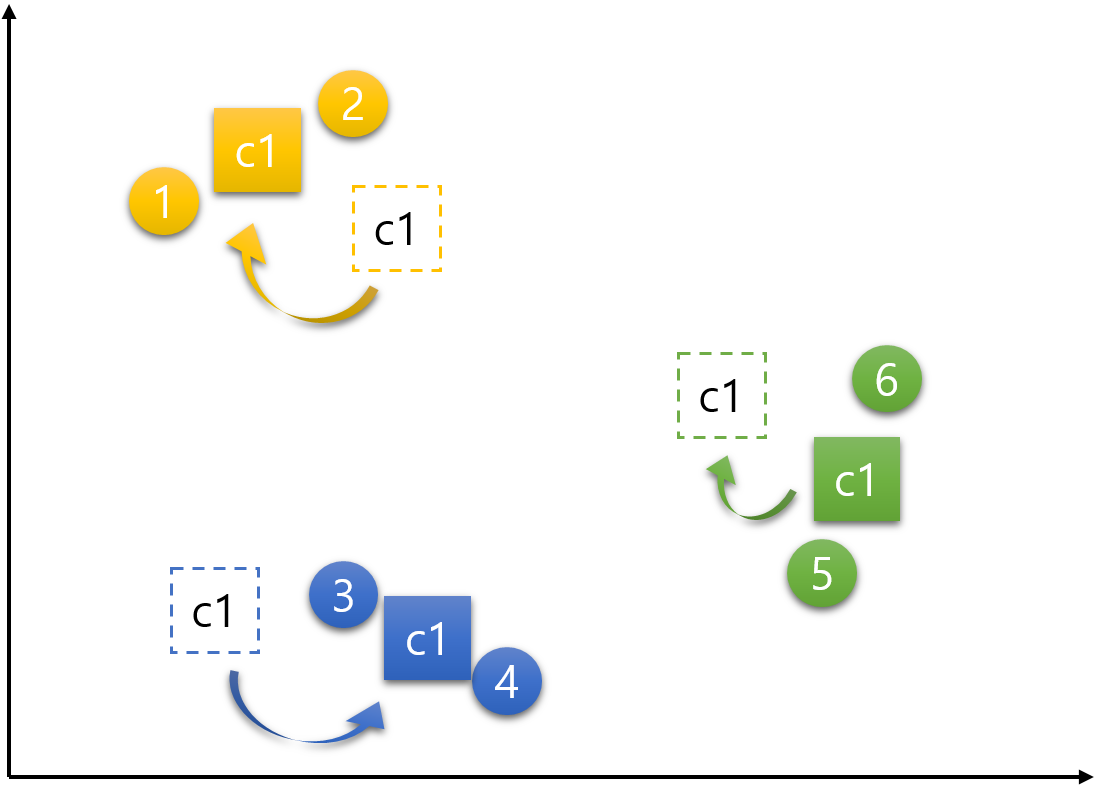
결국 다음과 같이 중심점들이 옮겨진다. 
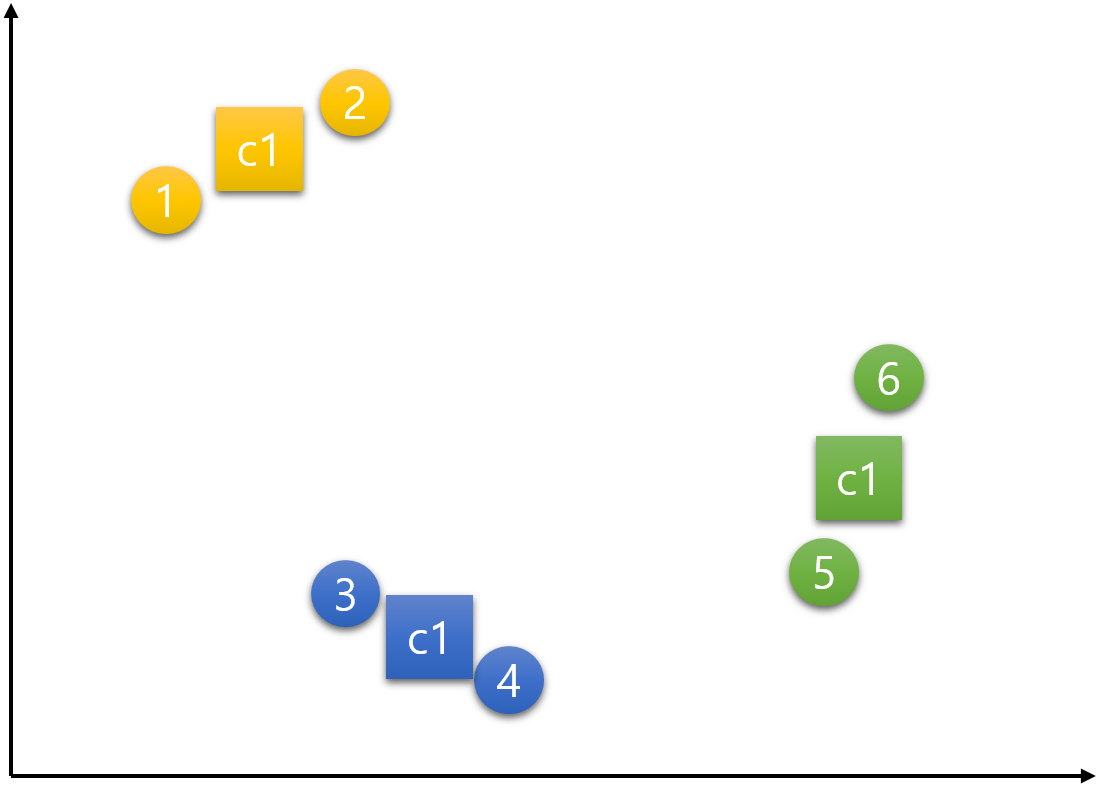이 세 점이 무게중심을 의미하는 Centroid 라고 불리는 이유는 데이터들의 무게중심의 위치로 이동하기 때문임을 알 수 있다.step 5) 데이터를 군집에 재할당(배정)하기
더 이상 중심점의 이동이 없을 때까지 step 4와 step 5를 반복한다고 했는데 위의 예시는 더 이상 이동이 없어 종료된다. 즉, 아래의 그림이 최종 결과이다.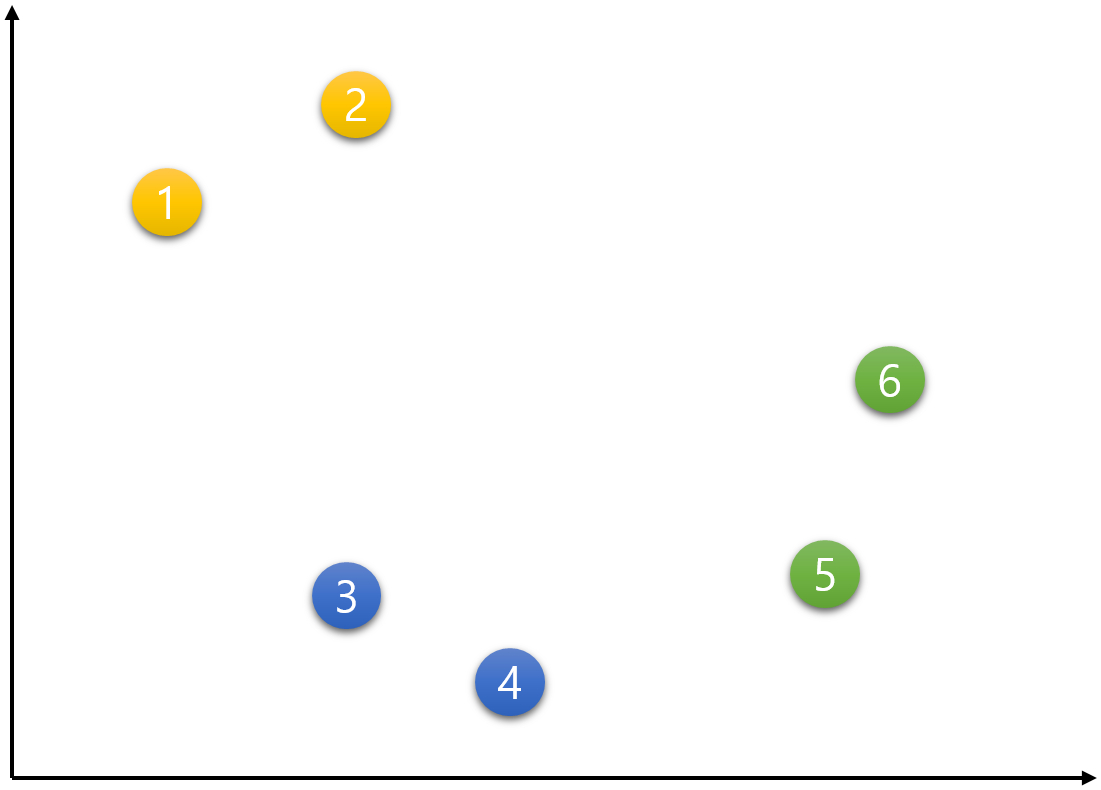
(바) 정리
K-means clustering(K-means 군집화)은 데이터를 입력받아 이를 연관된 K개의 그룹으로 묶는 알고리즘입니다. 이 알고리즘은 아래의 그림처럼 학습 시에 레이블이 없는 데이터를 입력받아
각 데이터를 특정 그룹으로 할당함해주는 알고리즘입니다.
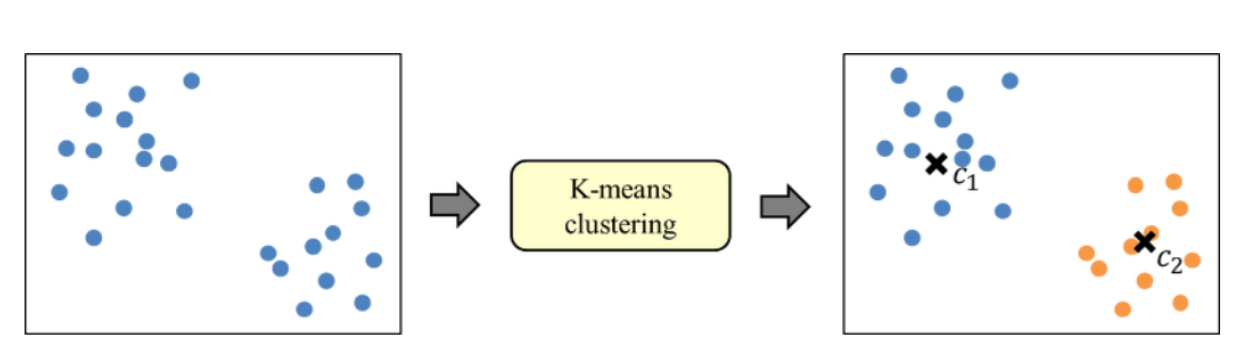
새로운 데이터가 들어오면, K-means 알고리즘이 어느 그룹인지를 판단하여 결정하고, 결정되면 해당 데이터에 특정 그룹이라는 레이블을 달아줍니다. 레이블이 이 알고리즘의 결과인 것이죠.
