목표

• 다익스트라 알고리즘을 이해한다.

다익스트라 알고리즘

• 다익스트라 알고리즘은 벨만 포드 알고리즘의 개선법
• 모든 값이 아닌 최소값에 대해서만 Relaxation 연산이 이루어짐
• 이미 Relaxation 연산이 이루어진 정점은 제외

동작

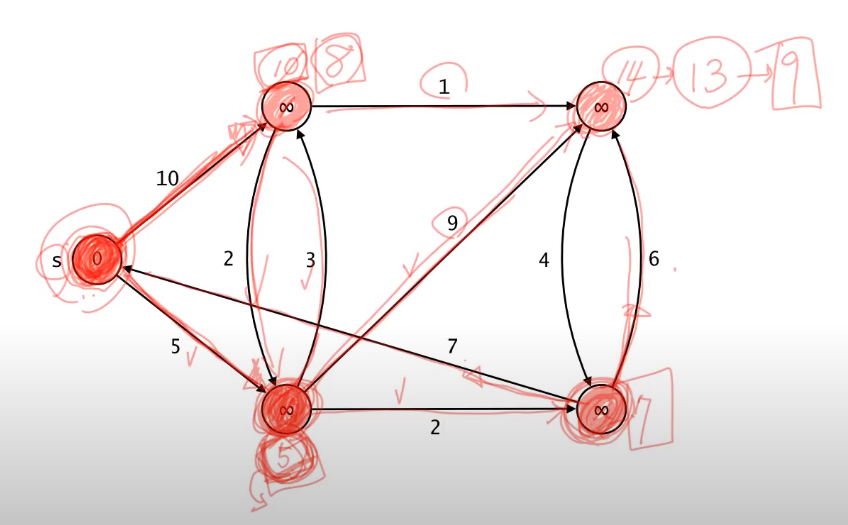
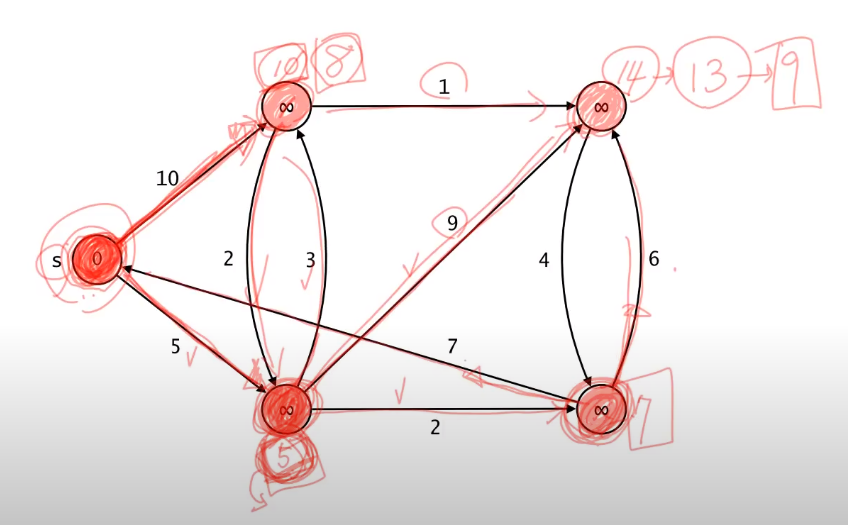
• 다익스트라 알고리즘은 최소값에 대해서만 Relaxation 연산이 이루어진다.
  1. 최소값을 가진 정점 $s$ 선택
  2. $s$에서 나가는 두 정점에 대해서 Relaxation이 이루어지는데 두 노드는 무한대니 각 8, 5가 된다.
  3. Relaxation이 이루어진 정점 $s$를 제외한 정점에서 최소값 $v(5)$인 정점 선택 후 Relaxation
  4. $v(10) = 8$ 나머지 무한대들은 14, 7이 된다.
  5. 다시 $v(7)$이 선택, $v(14)$는 $v(13)$으로 Relaxation
  6. 다시 $v(8)$ 선택, $v(5)$는 할 필요가 없으니 $v(13)$에 대해 Relaxation
  7. $n-1$개의 에지, $n$개의 노드를 모두 탐색했으니 최단 경로가 구성되고 종료

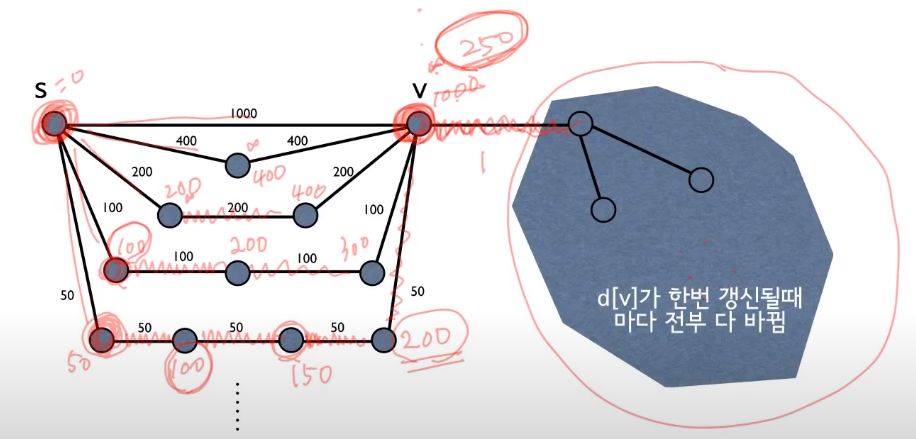
• 따라서 기존의 벨만포드와 달리 250에서 단 한번의 Relaxation만 이루어지면 된다.
  50 -> 100 -> 100 -> 150 -> 200 -> 200 -> 200 -> 250

다익스트라 알고리즘이 왜 최단 경로를 구성할까?

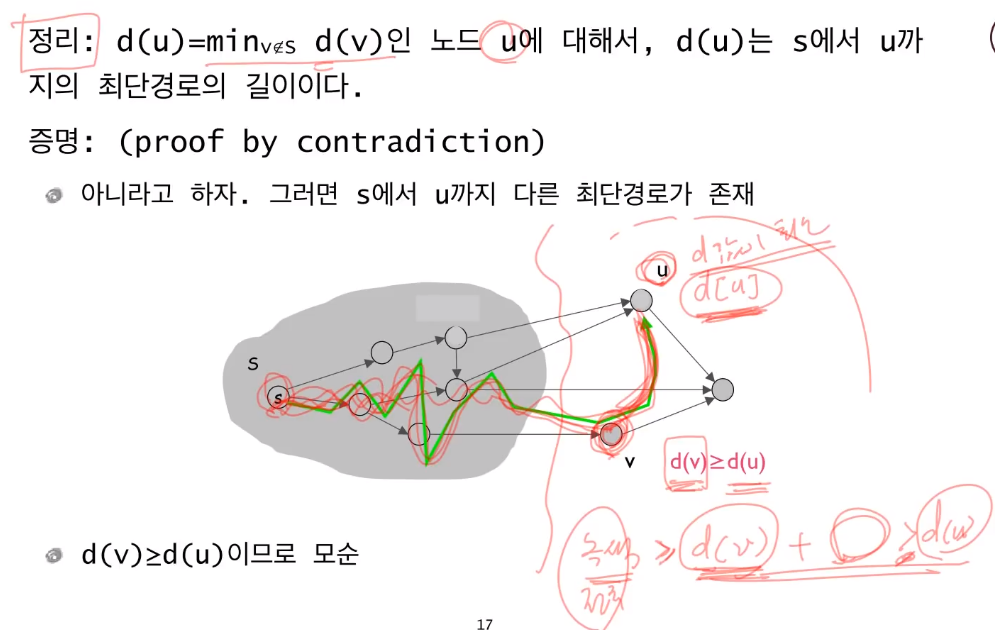
• 최단 경로가 구성된 집합 $S$와 나머지 집합이 있다고 한다면
  나머지 집합에서 최소값의 정점 $d[u]$는 $S$의 모든 최단 경로를 거쳐온 길이가 된다.
• 만약 최소값인 정점$d[u]$가 최소값이지만 최단 경로가 아니라면
  다른 어떤 정점을 하나를 더 거쳐야한다는건데
  이는 $S$의 최단 경로 > $d[v] + d[u + v] > d[u]$가 되고 최소값인 정점은 이미 기준 정점으로부터 최단 경로를 찾은 것에 위배된다.

구현법과 시간복잡도

• 시작 정점을 제외한 나머지에 대해 Relaxation이 이루어져야 하니 $n-1$번 반복
• 최단 경로 집합 $S$에 속하지 않은 정점 중 최소값을 찾아야하니 $O(n)$ 반복
• 그 정점을 Relaxation을 해야하니 $O(1)$ 반복

따라서 Lazy Dijkstra의 시간복잡도는 $O(n^2)$
그런데 최소값을 찾는 것은 최소 힙을 이용하면 $O(logn)$의 시간에 가능

• 따라서 최소 힙을 사용한다면 기존의 반복 $O(n)$
• 최소 힙 $O(logn)$
  그런데 힙은 항상 힙의 균형을 맞춰주는 작업이 필요한데 이는 최악의 경우 모든 노드에 대해 필요하다.

따라서 모든 노드에 대한 작업 $O(m)$과 힙 연산 $O(logn)$을 하면 최종적으로 $O(mlogn)$이 된다.

자바 인접리스트 다익스트라 알고리즘 구현

• 0621 23:30
  생각대로 막 구현하다 막혀서 다시 정리...
  • 구현 필요요소
    • Graph(u, v, w)
    • Priority Queue
    • 추정 거리를 담을 배열 dist[ ]
      --> 이거 생각 안하고 weight로 생각만 하고 있다가 어? 어? 해서 막힘
      무한대의 거리 그리고 노드 번호에 따른 거리를 계산하고 담을 배열이 필요하다
• 0622 16:30
  상당히 잘못 생각하고 있었음
  간선이 아닌 정점 기반이기때문에 간선처럼 간선 집합 $edgeSet(u, v,w)$가 아닌
  정점 집합 $vertexSet(v, w)$로 했어야 함
  인접 행렬은 쉬우니 다들 할 수 있을 것 같고 인접 리스트가 어색한 나같은 사람들을 위해 인접 리스트로 구현 함

자바 다익스트라 알고리즘 구현 코드

->전체 코드는 여기로

public void dijkstra(int start) {
            dist[start] = 0; // 시작 정점인 자기 자신에 대한 거리는 0
            PriorityQueue<vertexSet> pq = new PriorityQueue<>(); // 최소값
            vertexSet cur;
            pq.add(new vertexSet(start, 0)); // 1 -> 1, 가중치 0
            // 각 정점 비교
            while (!pq.isEmpty()) {
                cur = pq.poll(); // 시작 정점
                int curV = cur.v; // 시작 정점이 가진 다음 정점
                int curW = cur.w; // 시작 정점이 가진 가중치
                if (dist[curV] < curW) { // 가중치를 통한 거리 계산, 만약 기존 거리가 더 짧다면 패스
                    continue;
                }
                for (int i = 0; i < graph.get(curV).size(); i++) { // 인접 정점에 대한 Relaxation
                    int nextV = graph.get(curV).get(i).v; // 기준 정점으로부터 인접 정점
                    int nextW = graph.get(curV).get(i).w; // 기준 정점으로부터 인접 정점 가중치
                    if (dist[nextV] > curW + nextW) { // Relaxation
                        dist[nextV] = curW + nextW;
                        pq.add(new vertexSet(nextV, dist[nextV])); // Relaxation 후 다음 정점 추가
                    }
                }
            }
        }

실행 결과

graph.dijkstra(1);
System.out.println(Arrays.toString(dist));
Arrays.fill(dist, INF);
graph.dijkstra(5); // 방향 그래프라 6밖에 갈 수 없음
System.out.println(Arrays.toString(dist)); 

Task :dijkstraAlgorithm.main()
[2147483647, 0, 3, 2, 4, 10, 11, 2147483647, 2147483647]
[2147483647, 2147483647, 2147483647, 2147483647, 2147483647, 0, 1, 2147483647, 2147483647]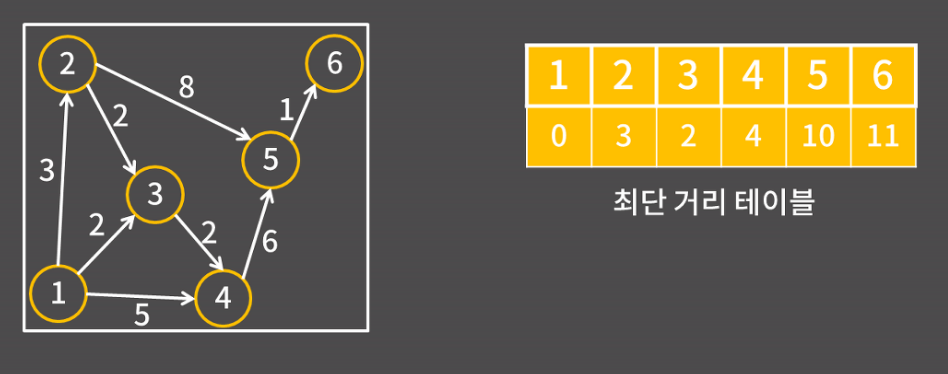

구현했던 그래프와 동일한 결과값이 나왔다.
1에서 각 정점으로 가는 최단 경로

• 1->2
• 1->3
• 1->3->4
• 1->3->4->5
• 1->3->4->5->6

결론

• 다익스트라 알고리즘은 벨만 포드의 개선 알고리즘이다.
• 음의 가중치는 없다고 가정한다.
• 정점 선택 기반으로 모든 정점을 알아야하는데 이는 메모리적으로 비효율적이다.
• 실제 내비게이션과 같은 최단 경로 탐색에는 A* 알고리즘이 더욱 많이 쓰인다.
• 다익스트라 알고리즘의 확장판이 A* 알고리즘이기때문에 몸에 익어야한다.

참고

바킹독 블로그
권오흠 알고리즘
영문 위키
Geek for Geeks
나동빈 실전 알고리즘 강좌