목표
- 트리에 대해서 이해한다
- 트리의 순회에 대해서 이해한다
- 이진 탐색 트리에 대해서 이해한다
- 이진 탐색 트리를 구현한다
- 이진 탐색 트리의 문제점과 해결 방법
트리
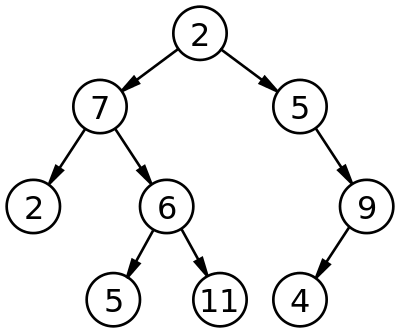
- 트리는 어떤 노드에 대해서 연관되는 노드로 구성되어진 자료구조다.
- 트리는 한 노드에 대해여 한개부터 여러개까지의 자식 노드가 존재할 수 있다.
- 트리의 값은 중복되거나 되지 않거나, 정렬되거나 정렬되지 않을 수 있다.
- Cycle이 없다.
각 노드의 loop는 존재하지 않는다.
- 트리는 그래프와 현실세계의 계층을 표현할 수 있는 자료구조다.
그래프는 객체 간의 관계를 표현하지만 계층은 표현할 수 없다
트리는 계층을 표현할 수 있으므로 객체 간 관계와 계층을 표시한 그래프는 트리다. - 트리의 모든 Edge 개수는 항상 Node - 1이다.
위 트리의 경우 2 7 5 2 6 5 11 9 4
9개의 노드, 8개의 에지를 가짐
트리의 순회
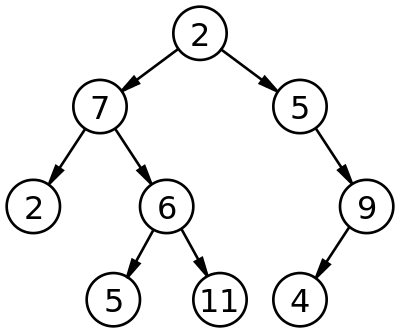
- PreOrder
Root -> Left -> Right
2 7 2 6 5 11 5 9 4 - InOrder
Left-> Root -> Right
2 7 5 6 11 2 4 9 5 - PostOrder
Left -> Right -> Root
2 5 11 6 7 4 9 5 2 - Level Order
레벨 순서 순회의 경우 각 노드의 레벨을 전부 순회하는 것으로 Depth First Search(DFS)라고도 한다.
말 그대로 레벨을 전부 순회하는 것
2 7 5 2 6 9 5 11 4
이진탐색트리
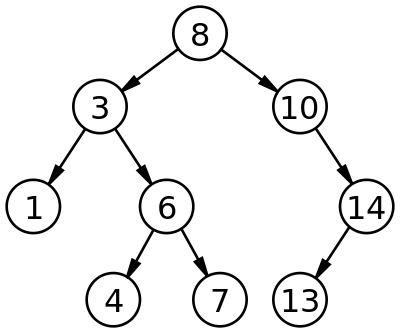
- 이진트리는 노드가 두개까지만 존재하는 트리
- 이진트리는 규칙에 따라 이진탐색트리로 구현된다.
leftNode <= RootNode < RightNode
이진탐색트리의 종류
- Binary Search Tree
BST의 규칙만 존재하는 이진탐색트리
최악의 경우 Skewed(치우친)트리가 된다.
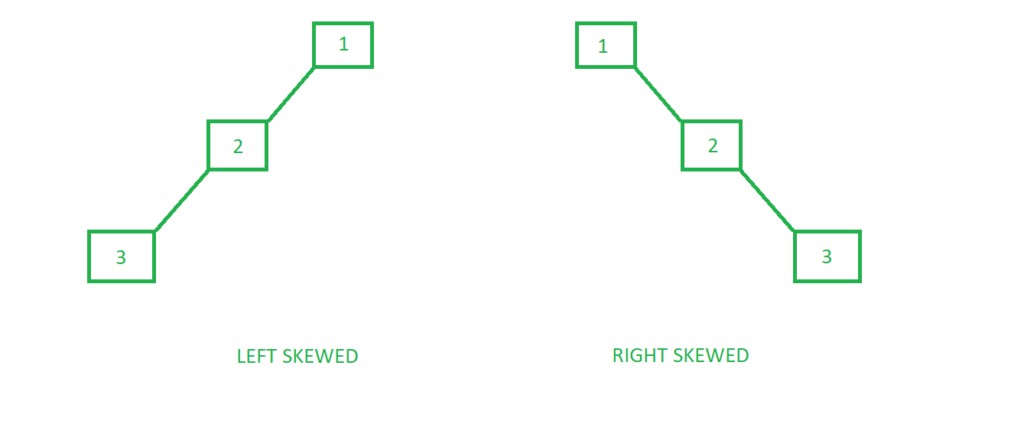
Skewed 트리가 될 경우 사실 상 연결리스트와 동일해지며 검색 시간은 O(n)이 되버린다.
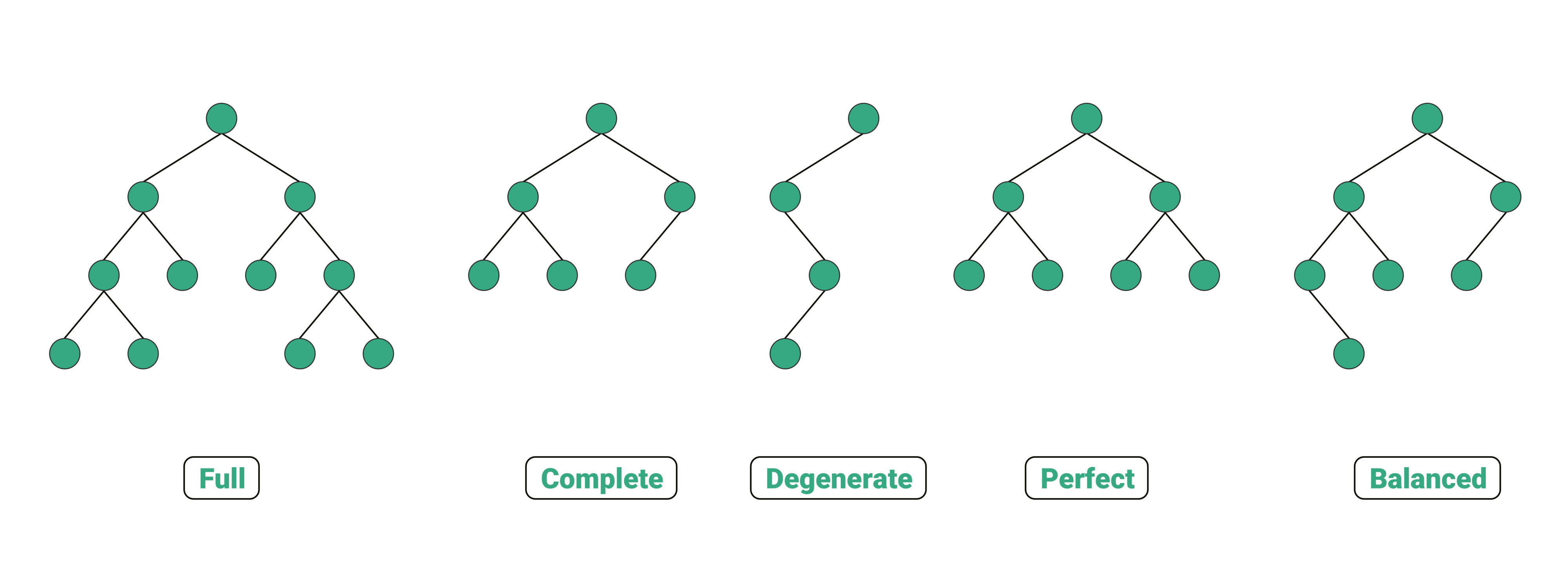
- Balnced Tree
Skewed 트리의 문제점을 해결하기 위해 레벨 균형을 맞추는 트리
AVL과 RED-BLACK 트리가 존재
-
Full Binary Tree
모두 존재하거나 모두 존재하지 않는 트리 -
Complete Binary Tree
마지막 레벨을 제외한 모든 레벨이 완전하고 왼쪽부터 채워진 트리 -
Perfect Binary Tree
레벨과 노드 갯수가 모두 동일한 트리로 Full + Complete임
이진탐색트리 구현
전체 코드
삽입
public void addChild(int input) { // 노드 삽입
// 노드 값이 중복되면 삽입없이 종료
if (searchingNode(input) != null) {
System.out.println("already exist in tree " + input);
return;
}
Node newNode = new Node(input);
if (root == null) { // 트리가 없다면 root 생성
root = newNode;
} else {
Node moveNode = root; // 움직일 노드
Node pointer;
while (true) {
pointer = moveNode;
if (input < pointer.data) {
moveNode = pointer.left;
if (moveNode == null) {
pointer.left = newNode;
return;
}
} else {
moveNode = pointer.right;
if (moveNode == null) {
pointer.right = newNode;
return;
}
}
}
}
}삭제
개인적으로 트리의 삭제가 약간 헷갈렸다.
트리의 삭제는 세가지가 존재하는데 자식 노드가 두개 다 존재할 경우 트리의 구조를 유지시켜야 하기때문에 몇가지 조작이 필요했다.
- 자식 노드가 없을 경우
- 자식 노드가 하나만 존재할 경우
- 자식 노드가 두개 다 존재할 경우
public void deleteNode(int input) {
Node moveNode = root;
Node pointer = root;
boolean leftflag = true;
// 삭제 될 노드로 이동
while (moveNode.data != input) {
pointer = moveNode;
if (input < moveNode.data) {
leftflag = true;
moveNode = pointer.left;
} else {
leftflag = false;
moveNode = pointer.right;
}
}
Node replacementNode; // 변경될 노드
// 자식 노드가 없는 노드 삭제
if (moveNode.left == null && moveNode.right == null) {
if (moveNode == root) {
root = null;
}
if (leftflag) {
pointer.left = null;
} else {
pointer.right = null;
}
}
// 자식 노드가 한개 있는 노드 삭제
// 어차피 왼쪽만 있은 왼쪽만 지우면 끝
else if (moveNode.right == null) {
if (moveNode == root) {
root = null;
}
pointer.left = null;
}
// 오른쪽만 있다면 오른쪽만 삭제
else if (moveNode.left == null) {
if (moveNode == root) {
root = null;
}
pointer.right = null;
}
// 자식 노드가 두개일 때
else {
// 삭제될 노드의 오른쪽 트리 저장
Node subTree = moveNode.right;
// 삭제될 노드의 서브트리에서 가장 작은 노드 확인
replacementNode = subTree.left;
subTree.left = null;
// root 라면 그냥 바꿔줌
if (moveNode == root) {
root = replacementNode;
}
// flag 통해서 root 좌우측 판단
if (leftflag) {
pointer.left = replacementNode;
} else {
pointer.right = replacementNode;
}
// 바꿀 노드가 null이 아니라면
// 바꿀 노드의 오른쪽에 서브트리 결합
// 바꿀 노드가 서브트리면 null
// 바꿀 노드의 왼쪽에 기존 노드의 좌측 노드 결합
if (replacementNode != null) {
replacementNode.right = subTree;
if (replacementNode == subTree) {
replacementNode.right = null;
}
replacementNode.left = moveNode.left;
}
}
}순회
- InOrder
public void inOrder(Node node) { // left - root - right if (node != null) { inOrder(node.getLeft()); System.out.println(node.data); inOrder(node.getRight()); } }
- PreOrder
public void preOrder(Node node) { // root - left - right if (node != null) { System.out.println(node.data); preOrder(node.getLeft()); preOrder(node.getRight()); } }
- PostOrder
public void postOrder(Node node) { // left - right - root if (node != null) { postOrder(node.getLeft()); postOrder(node.getRight()); System.out.println(node.data); } }
실패 코드
비교 조건문이 잘못된 우편향 트리
실패코드가 아니였음
이진탐색 트리의 조건에 따르면 left < root < right인데 [1, 2, 3, 4, 5, 6, 7]을 집어넣을 경우 이진탐색 조건에 의해 root (1) 보다 삽입되는 모든 데이터가 크니 우편향 트리 생성
public void addChild(int input) {
Node newNode = new Node(input);
if (root == null) { // 트리가 없다면 root 생성
root = newNode;
count++;
} else {
Node pointer = root; // 포인터
Node parent; // 포인터의 부모
while (true) {
parent = pointer;
if (input < parent.data) {
pointer = parent.left;
if (pointer == null) {
parent.left = newNode;
count++;
return;
}
} else {
pointer = parent.right;
if (pointer == null) {
parent.right = newNode;
count++;
return;
}
}
}
}
}- 노드 조건을 생각해서 구현했지만 조건문이 잘못된 트리
알고보니 균형이진트리를 구현하던 것이였음
Node pointer = root; // 포인터
Node parent; // 포인터의 부모
while (true) {
parent = pointer;
if (count % 2 == 1) {
pointer = parent.left;
if (pointer == null) {
parent.left = newNode;
count++;
return;
}
} else {
pointer = parent.right;
if (pointer == null) {
parent.right = newNode;
count++;
return;
}
}이진탐색트리의 문제점과 해결방법
- 이진탐색트리는 평균적으로 O(logN)의 검색/삽입/삭제 속도를 가진다.
이진이기에 노드의 검색은 모든 연산에서 절반씩 감소한다. - 하지만 최악의 경우 Skewed Tree가 되며 O(N)의 속도로 감소한다.
- 이진탐색트리의 균형을 맞추어줘야 O(logN)의 평균값을 가질 수 있다.
RED-BLACK Tree와 AVL Tree를 구현하여 균형이진트리를 구현할 수 있다.
RED-BLACK & AVL
