목표
- Red-Black 트리를 이해한다.
- AVL 트리를 이해한다.
RED-BLACK 트리
- 이진 검색 트리는 평균적으로 의 삽입, 삭제, 검색 연산속도를 가진다.
- 이진 검색 트리의 구성 조건은 left < root < right
이런 조건에 따라서 랜덤한 데이터가 아닌 순차정렬 된 데이터가 들어올 때
이진 검색 트리는 편향 트리가 된다.
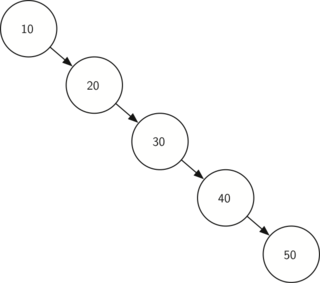
- 트리의 속도는 트리의 깊이에 따라 결정 되기에 편향 트리의 시간복잡도는 까지 늘어난다.
이러한 일을 방지하기 위해서 트리 깊이의 균형을 Red-Black 트리를 통해 맞출 수 있다.

이렇게 트리의 깊이가 균형이 맞게 된다면 이진 탐색 알고리즘의 속도와 비슷해져서 아주 효율적으로 사용할 수 있다. - 자바에서는 treeSet, treeMap이 Red-Black 트리를 구현하고 있다.
Red-Black 트리의 구성

조건
-
트리의 모든 노드는 레드 or 블랙
그림과 같이 트리는 레드와 블랙으로만 구성되어 있다. -
루트 노드는 무조건 블랙
루트 13은 블랙이다. -
모든 리프 노드(자식 없는 노드)는 블랙(Sentinel Node가 블랙인거에 유의)
-
루트 노드에서 리프 노드까지 블랙의 갯수는 항상 같다.
그림 상 있는 NIL까지 도달할 때 보더라도
리프 노드 6은 블랙 노드 1을 만난다.
리프 노드 22는 블랙 노드 25를 만난다.
리프 노드 27은 블랙 노드 25를 만난다. -
레드 노드의 자식은 모두 블랙, 블랙 노드의 자식은 상관없음
동작
- 레드-블랙 트리도 이진 탐색 트리기때문에 탐색, 삽입, 삭제 연산으로 동작한다.
- 탐색 연산은 변경할 필요가 없으나 삽입, 삭제 연산의 경우 균형을 맞춰주는 동작이 필요하다.
Restructuring, Recoloring 연산
자신(Z)과 부모 노드(V)가 레드라면
- 삼촌 노드(W)가 블랙일 때 Restructuring(Rotation)
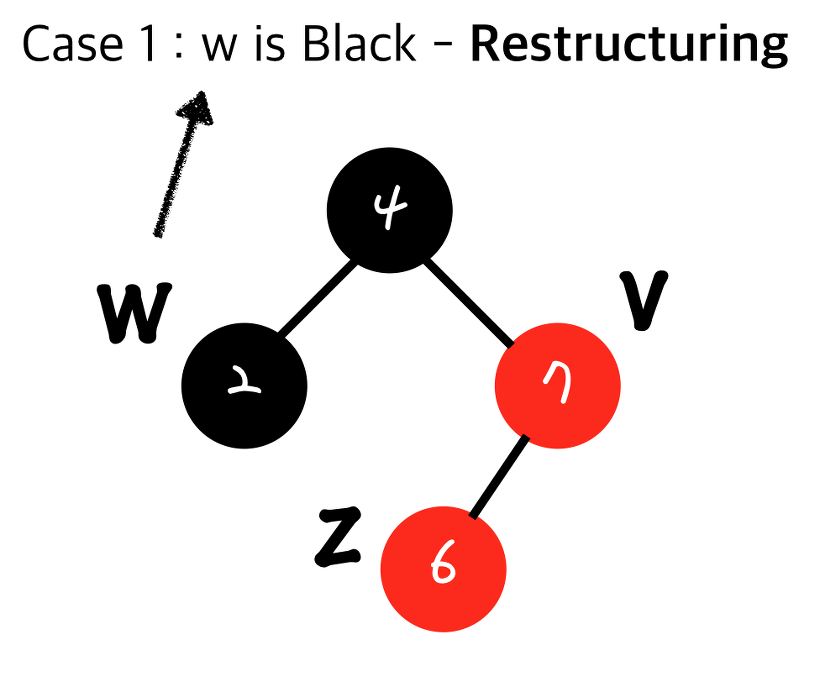
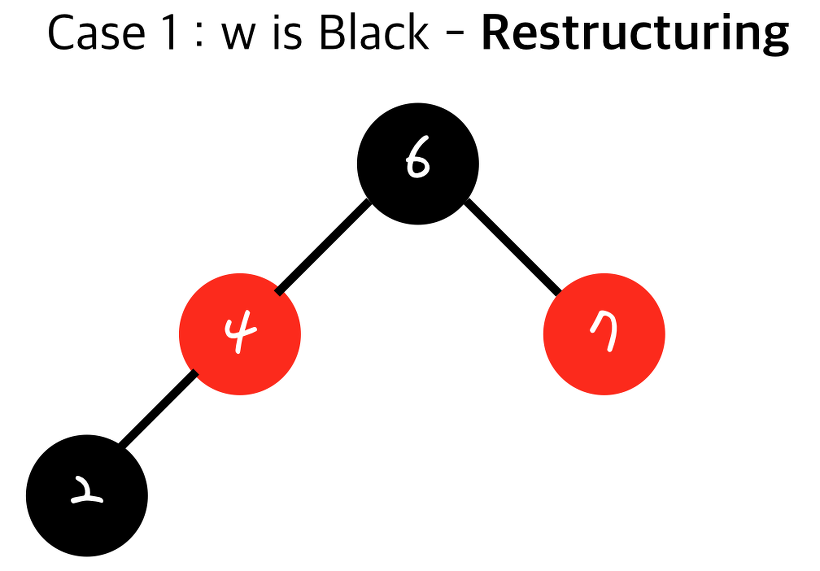
- 나(Z)와 내 부모(V), 내 부모의 부모(조상)을 오름차순으로 정렬한다
- 무조건 가운데 있는 값을 부모로 만들고 나머지 둘을 자식으로 만든다
- 올라간 가운데 있는 값을 블랙으로 만들고 그 두 자식들을 레드로 만든다
- 삼촌 노드(W)가 레드일 때 Recoloring
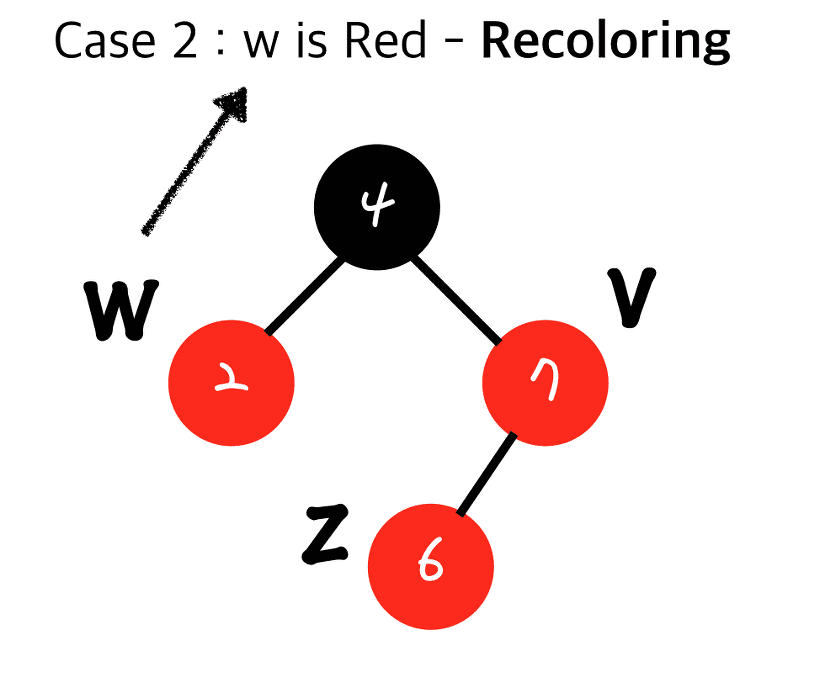
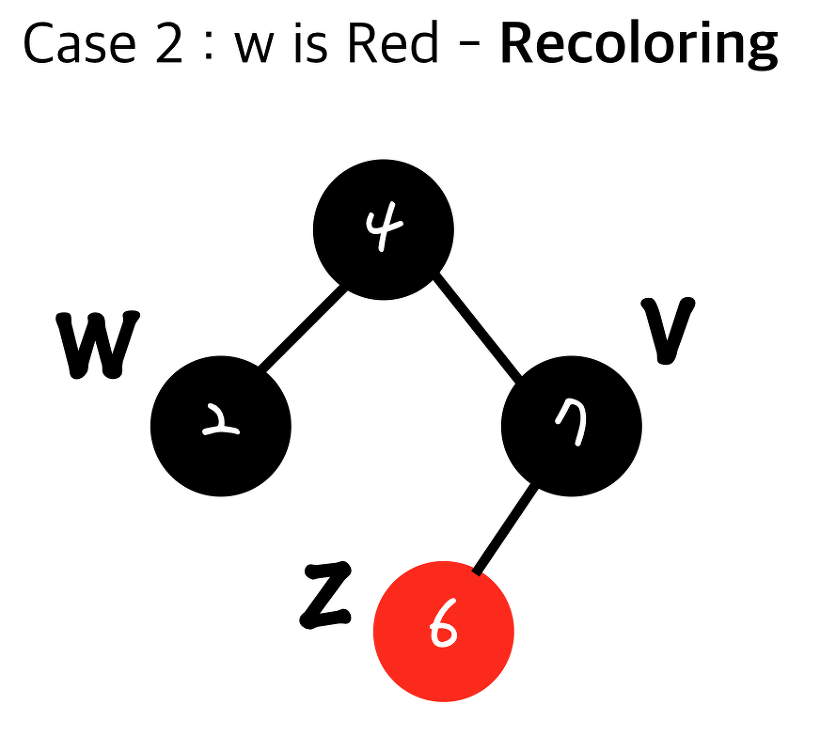
- 삽입된 노드(Z)의 부모와 삼촌(W)을 블랙으로 하고 부모의 부모를 레드로 만든다
- 내 부모의 부모가 Root가 아니었을 시 더블 레드가 다시 발생 가능
시뮬레이터를 통한 동작
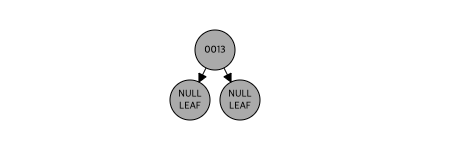
- 13 삽입, 루트, 검정
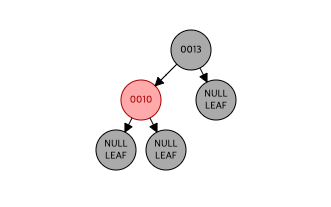
- 10 삽입, 레드
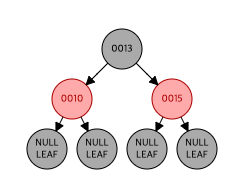
- 15 삽입, 레드
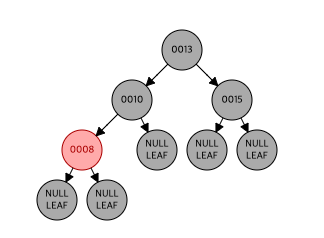
- 8 삽입, 레드
더블 레드가 발생했다.
자신(8)도 레드고 부모(10)도 레드라면 삼촌 노드(15)를 확인
삼촌 노드가 레드니 recoloring이 때 부모의 부모를 레드로 만들어야하나 그렇게 되면 루트는 블랙이라는 규칙에 위배 되므로 다시 검정으로 변경한다.
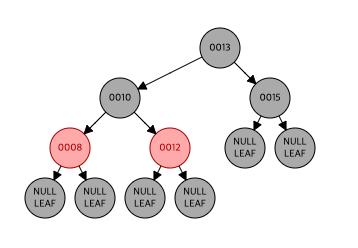
- 12 삽입, 레드
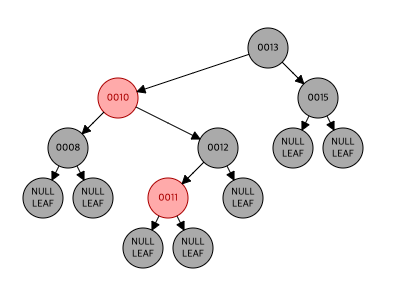
- 11 삽입, 레드
또 더블 레드가 발생
삼촌 노드(8)을 확인 해보니 레드, recoloring
- 12 삽입, 레드
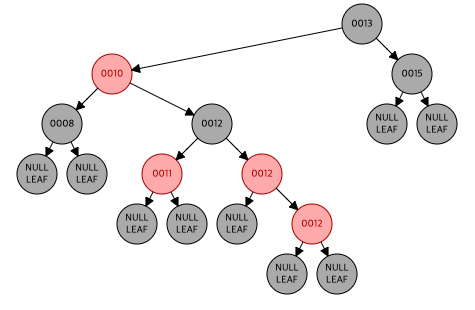
- 12 삽입, 레드
더블 레드로 인해 삼촌 노드(11) 확인, 레드니까 recoloring
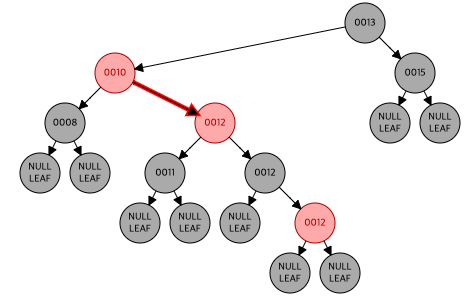
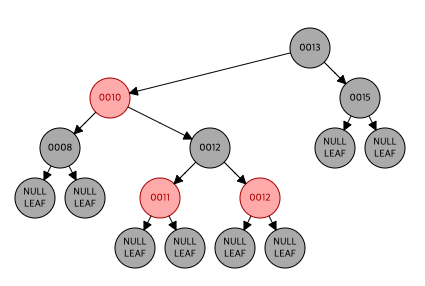
- recoloring을 했는데 더블 레드가 발생
더블 레드가 발생한 (12)의 삼촌 노드(8)을 확인했는데 블랙이니 restructuring
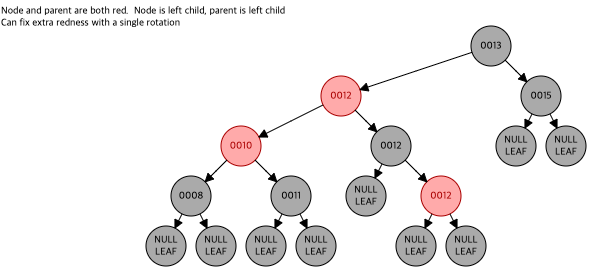
- right double red니 left rotation을 통해 레드를 제거
다시 더블 레드가 발생
left double red는 right rotation을 통해 제거
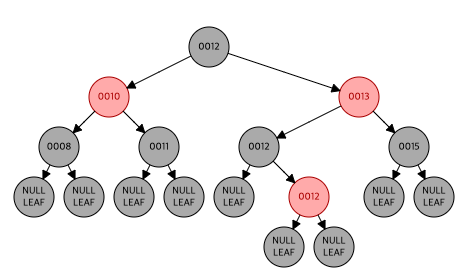
- 중복값들을 이용하여 시뮬레이션을 돌려서 좀 헷갈리긴 하는데
요컨대 더블 레드가 발생 시 어떤 기준에 의해 restructuring, recoloring 통해 균형이 맞추어 지는지 알 수 있고 결국에 중요한 건 트리의 높이라는 걸 알 수 있다. - 그래서 균형이 맞춰지는가?
레드 블랙 트리의 균형을 책임지는 건 "루트부터 리프까지 블랙 노드의 개수는 같아야한다."
레드는 중복될 수 없으니 반드시 레드와 레드 사이엔 하나의 블랙 노드를 끼게 되고 이는 곧 레드 블랙 트리의 총 깊이가 된다.결국 블랙 노드만을 가지는 가장 짧은 깊이와 블랙-레드의 차이는 최대 2배의 차이밖에 나지않는다.
루트-블랙-블랙-블랙-블랙 = 4
루트-레드-블랙-레드-블랙-레드-블랙-레드-블랙 = 8 / 2 = 4
AVL 트리
AVL트리가 나온 이유도 Red-Black 트리와 동일한데 다른 점은 Balnce Factor(BF)를 통해 균형을 맞춘다.
- BF는 -1, 0, 1로 이루어져 있으며 이 범위를 벗어난다면 그 트리의 균형은 깨진거다.
- 왼쪽 서브 트리에서 오른쪽 서브트리를 뺀 값이 그 노드의 BF가 된다.
Roatation
BF 값을 통한 균형은 을 통해 이루어진다.
rotation은 BF가 2 이상, -2 이하로 바뀐 노드를 기준으로 rotation이 이루어진다.
Single Rotation
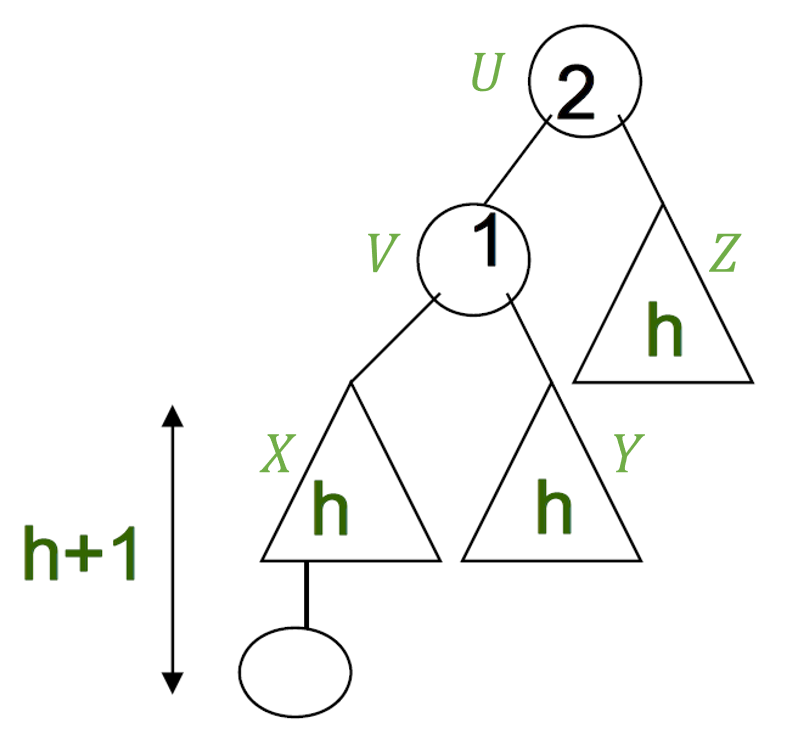
- x에 값 삽입 시 오른쪽 서브트리(3) - 왼쪽 서브트리(1) = 루트(2)
왼쪽 서브트리 v의 서브트리는 2 - 1 = v(1)
루트의 BF가 2 이므로 ratation이 일어나야 한다.
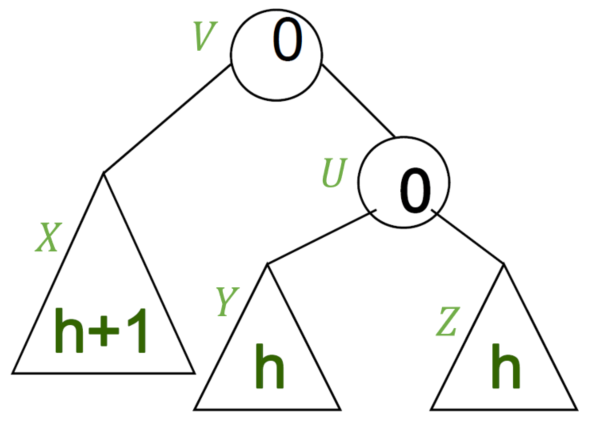
-
v를 새로운 루트 노드로 만들기 위해 오른쪽 서브트리 z를 내려 정렬한다.
이진 탐색 트리의 조건은 left <= root <= right 기에 z를 내려도 조건에 부합한다. -
값을 통한 예
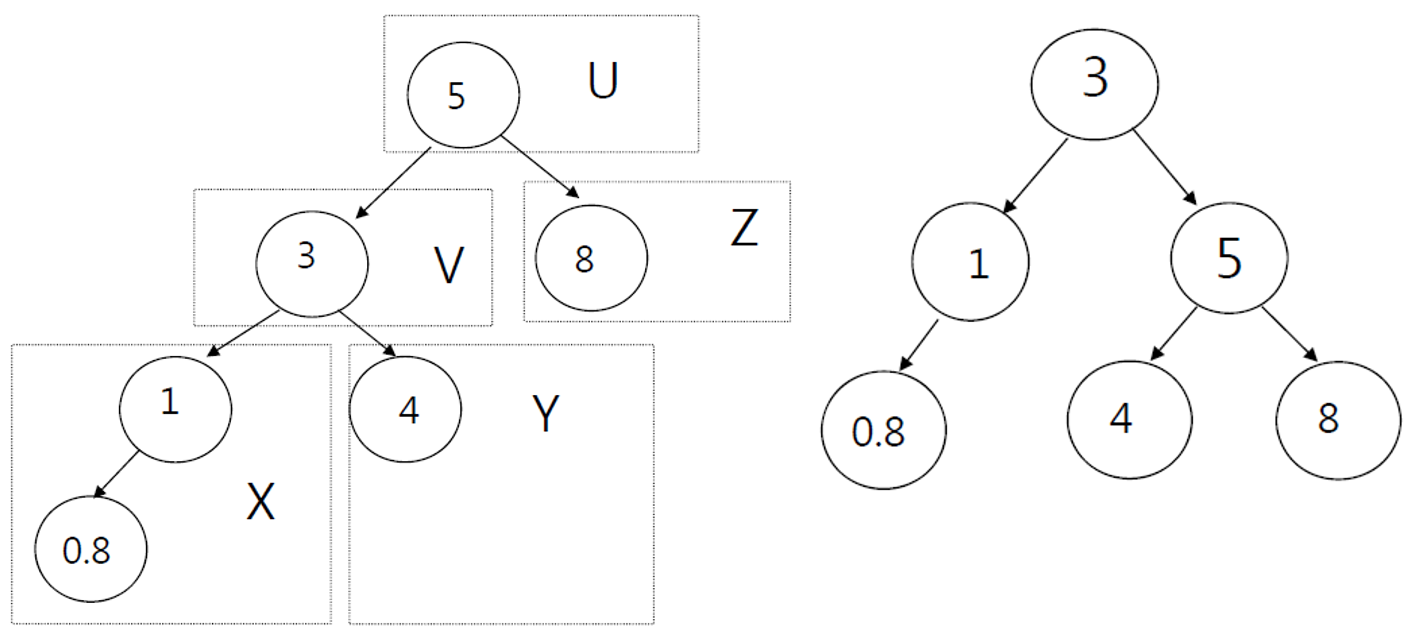
-
Right & Left

Double Rotation
- 만약 한번의 rotation만으로 균형을 맞추지 못할 때 다시 연산이 필요하다.
- 루트의 BF 값이 2 이상, 삽입되는 노드의 조상노드가 루트의 자식이면서 BF가 1 이하인 경우
- 루트의 왼쪽 자식 노드의 오른쪽 서브트리에 새 노드 삽입
- 루트의 오른쪽 자식 노드의 왼쪽 서브트리에 새 노드 삽입
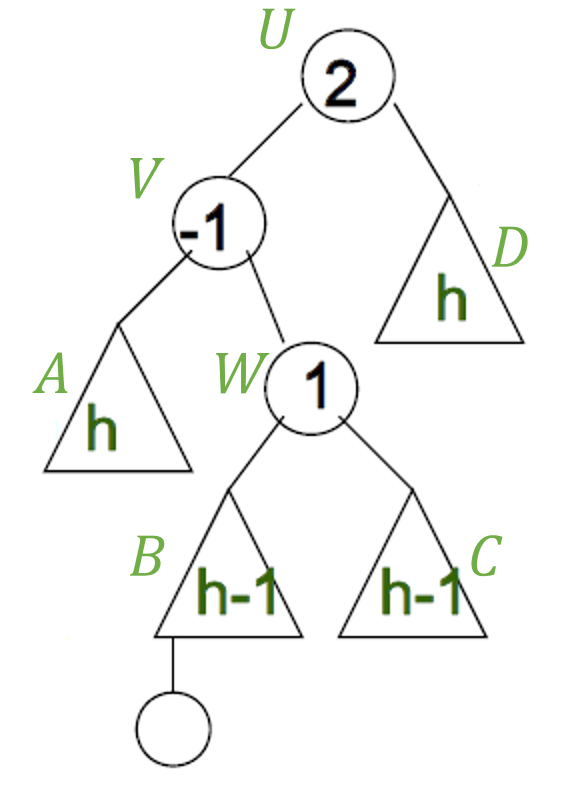
- 루트 u의 BF 값이 2, 삽입되는 노드의 조상 노드 v는 루트의 자식이면서 BF -1
그리고 v는 루트의 왼쪽 자식 노드, 새 노드는 v의 오른쪽 서브 트리에 삽입 되었기에double rotation 요건에 부합한다.
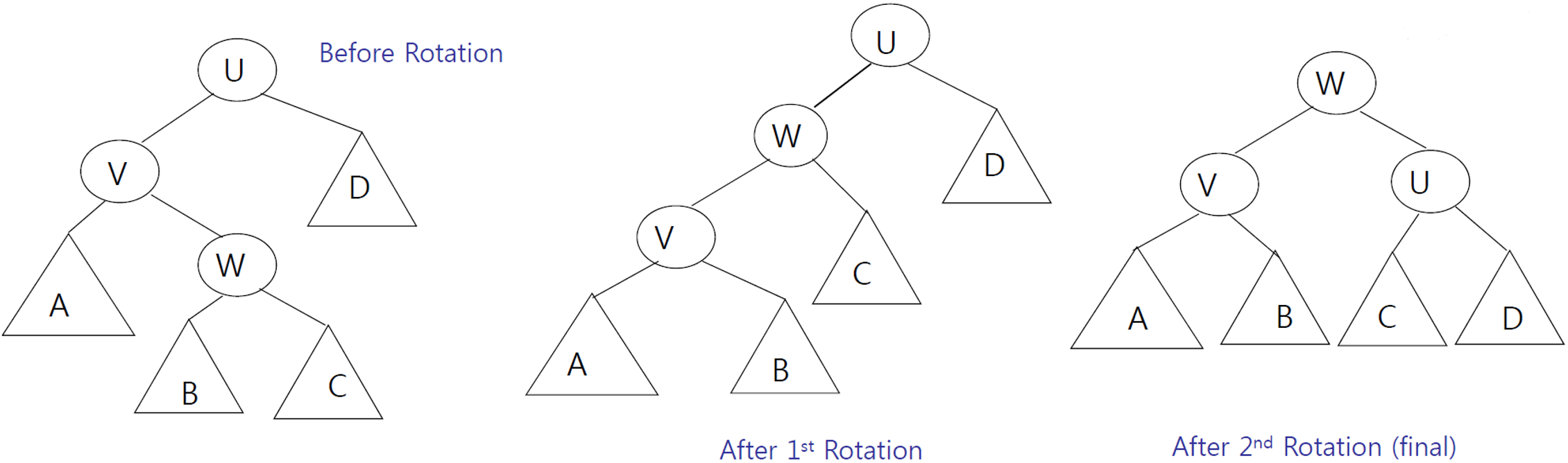
-
첫번째 : W를 중심으로 left rotation 수행 (A를 잡아 당겨 내리는 과정)
-
두번째 : W를 중심으로 right rotation 수행 (D를 잡아 당겨 내리는 과정)
- 균형
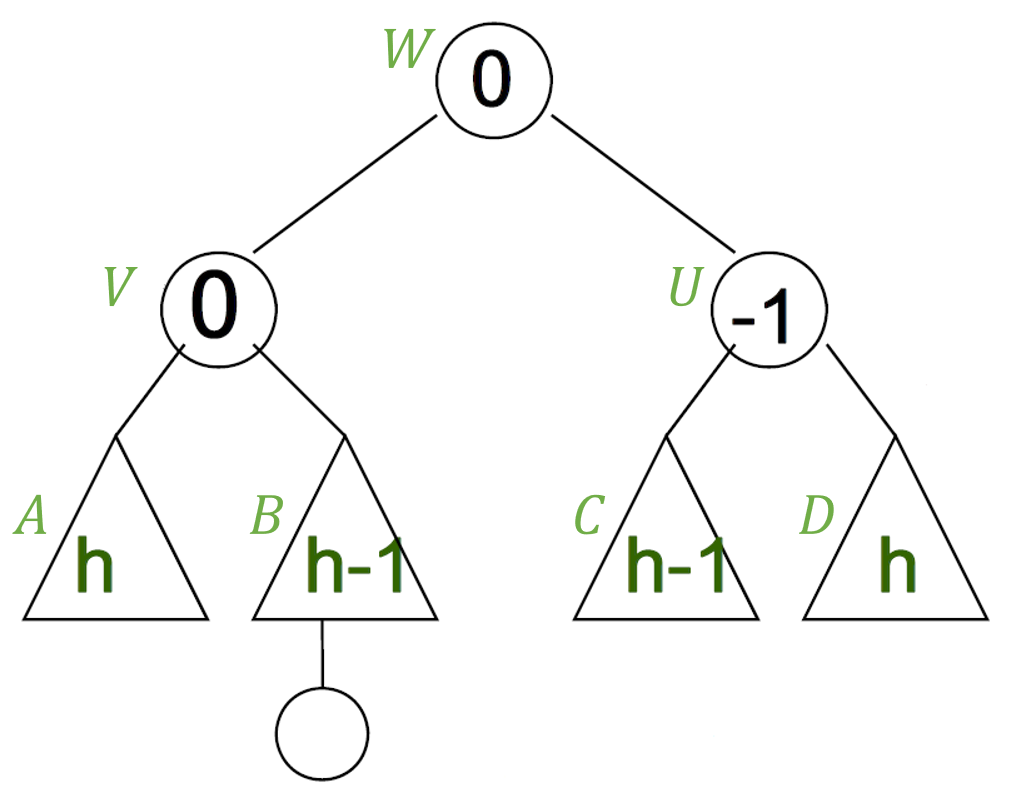
- 균형
-
값을 통한 예
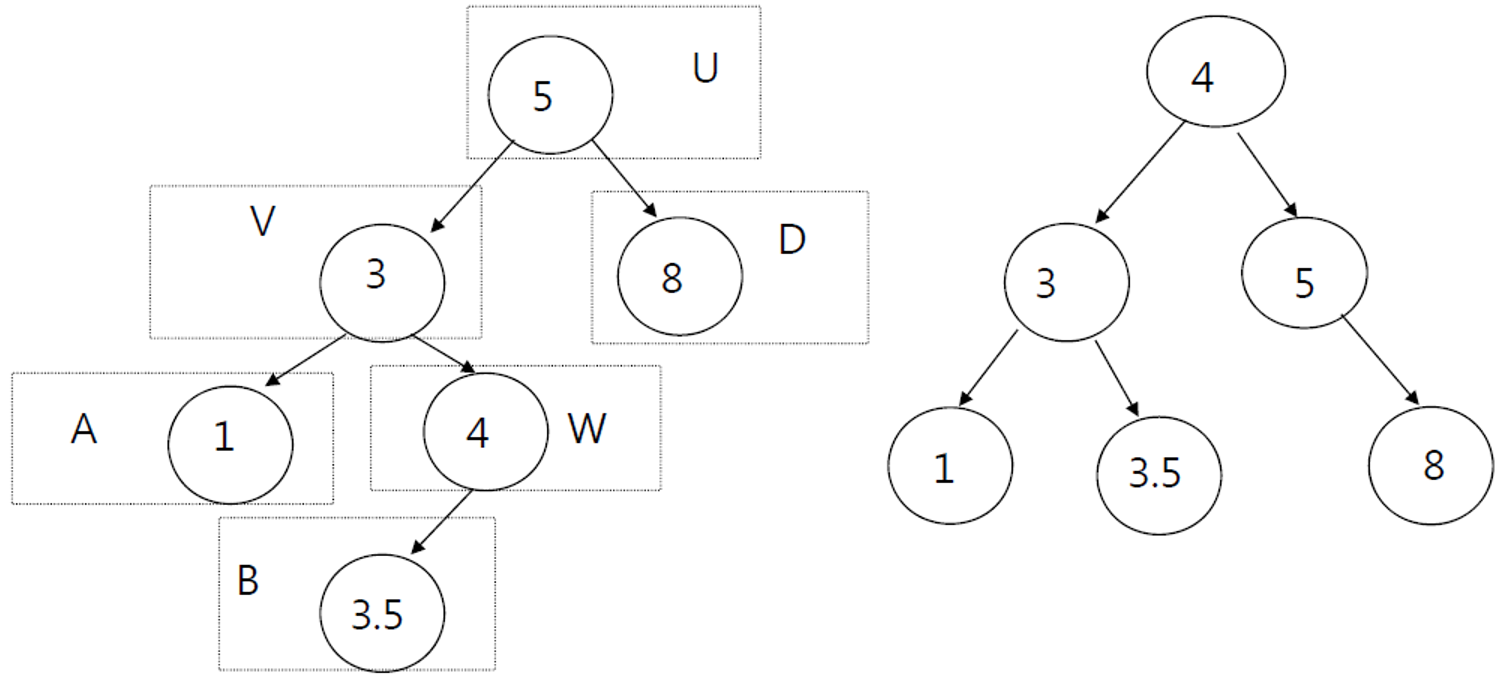
- v = -1, u = 2
- 조건 판단
- double rotation
- w 기준 left rotation
- w 기준 right rotation
- 루트는 0, 왼쪽 서브트리 0, 오른쪽 서브트리 -1로 균형
Red-Black vs AVL
- AVL트리는 더욱 엄격한 균형을 이루고 있기 때문에 Red-Black 트리보다 더 빠른 조회를 제공
- Red-Black 트리는 상대적으로 느슨한 균형으로 인해 회전이 거의 이루어지지 않기 때문에 AVL트리보다 빠르게 삽입 및 제거 작업을 수행
- AVL트리는 각 노드에 대해 BF를 저장하므로 노드 당 int 저장이 필요
Red-Black 트리는 노드당 1비트의 정보만 필요합니다. (플래그 반전만 시키면 됨) - Red-Black 트리는 맵, C++의 멀티캐스트, Java treeMap 등 대부분의 언어 라이브러리에서 사용, AVL트리는 더 빠른 검색이 필요한 데이터베이스에서 사용
