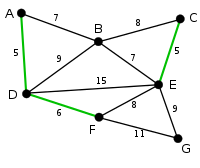
목표
- 크루스칼 알고리즘을 이해한다.
Kruskal's Algorithm

- MST를 구현하기 위해 사용하는 알고리즘
- 간선(edge) 선택 기반
- Greedy(탐욕적인) 알고리즘을 사용
- 모든 노드의 간선 집합을 비교
- 개의 Edge를 구성 시 종료
- 연산 속도는 cycle 형성 검사 속도가 결정
구현법
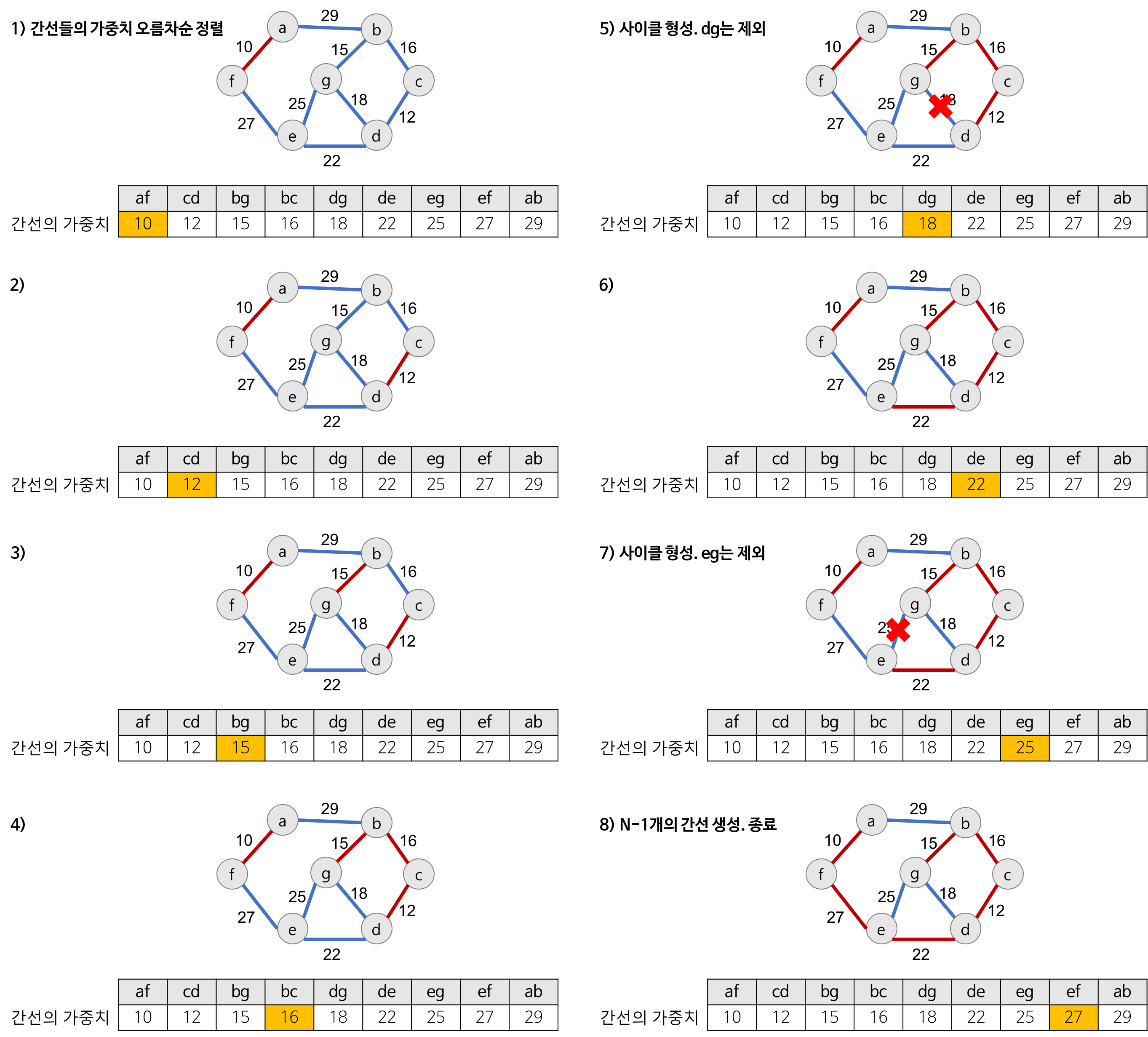
참고한 블로그 중 한눈에 보이는 사진이 있어 스크랩(출처)
- edge들은 가중치의 오름차순 정렬
- 정렬된 edge 중 가중치가 제일 낮은 edge부터 하나씩 선택
만약 선택하는 edge와 선택된 edge가 Cycle을 이룬다면 선택 안함
--> 동일한 집합이 아니라면 그 집합들의 어느 정점에서도 연결되지 않았으므로 Cycle 미형성 따라서 안전하다. - edge가 개 선택될 때까지 반복
Pesudo Code
algorithm Kruskal(G) is
A := ∅
for each v ∈ G.V do
MAKE-SET(v)
for each (u, v) in G.E ordered by weight(u, v), increasing do
if FIND-SET(u) ≠ FIND-SET(v) then
A := A ∪ {(u, v)}
UNION(FIND-SET(u), FIND-SET(v))
return A- 구현법을 의사 코드로 구현했을 때 필요한 작업은 FIND-SET(집합 찾기)와 UNION(합치기)
- 따라서 Disjoint Set(서로소/분리 집합)을 만들고 집합을 검색, 생성할 수 있는 자료구조가 필요
이는 Union-Find을 이용Cycle 검사는 Union-find 알고리즘을 이용
Union-find는 여기로
왜 Kruskal's Algorithm을 쓰면 MST를 만들 수 있을까?
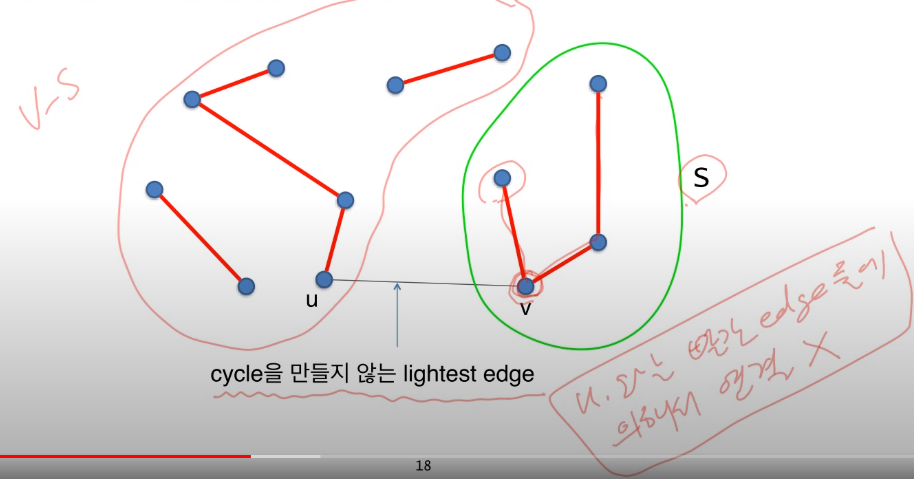
- kruskal이 진행 중에 cycle이 형성되지 않은 정점 를 가진 간선집합 와
정점 를 가진 간선집합 가 있다면 이 둘은 연결되지 않았다. - 정점 와 정점는 연결되지 않았기에 이 간선집합의 어떤 부분을 연결해도 Cycle은 형성되지 않는다 즉 간선집합 와 는 안전한 edge를 가진다.
특징과 시간복잡도
- 시간복잡도는 edge e의 개수에 따른 의 속도를 가짐
- 초기 edge 오름차순 정렬
- union-find를 통한 vertex 비교
- = 와 동일함
- edge 정렬이 속도를 결정짓기 때문에 edge 수가 적은 Sparse Graph의 경우 유리
자바 크루스칼 알고리즘 구현
- 정점은 n개, 에지는 n - 1개
- 간선집합을 오름차순 정렬하여 낮은 가중치부터 탐색
- union find 사용
어떻게 구현할까...
간선 집합 클래스
static class edgeSet implements Comparable<edgeSet> {
int u, v, w;
edgeSet(int u, int v, int w) {
this.u = u;
this.v = v;
this.w = w;
}
@Override
public int compareTo(edgeSet edgeSet) {
// the value 0 if x == y; a value less than 0 if x < y; and a value greater than 0 if x > y
return Integer.compare(this.w, edgeSet.w);
}
@Override
public String toString() {
return "U= " + this.u + " V= " + this.v + " W= " + this.w;
}
}- edge(u, v, w) 중 가중치 w로 비교 정렬하기 위해 Comparable 구현
Integer.compare(int a, int b)를 쓰면 알아서 정렬 됨the value 0 if x == y;
a value less than 0 if x < y;
and a value greater than 0 if x > y
rank by union & find
public void rankUnion(int x, int y) {
x = find(x);
y = find(y);
// 동일 루트면 종료
if (x == y) {
return;
}
// 트리 x보다 y가 작다면 x를 작게 만듬
if (rank[x] > rank[y]) {
tree[y] = x;
} else { // 반대면 반대로
tree[x] = y;
}
// 만약 트리 둘의 레벨이 같다면 union 됐으니 레벨 1 증가
if (rank[x] == rank[y]) {
rank[x]++;
}
}
public int find(int x) {
return (tree[x] == x) ? x : (tree[x] = find(tree[x]));
}main
public static void main(String[] args) {
unionFind union = new unionFind(1000);
Graph graph = new Graph(1000);
graph.makeEdge(1, 2, 4);
graph.makeEdge(1, 4, 2);
graph.makeEdge(4, 5, 7);
graph.makeEdge(4, 2, 12);
graph.makeEdge(2, 6, 8);
graph.makeEdge(2, 7, 1);
graph.makeEdge(4, 7, 3);
Collections.sort(graph.getGraph());
for (edgeSet i : graph.getGraph()) {
System.out.println(i.toString());
}
int sum = 0;
for (edgeSet edge : graph.getGraph()) {
if (!union.connected(edge.u, edge.v)) {
sum += edge.w;
union.rankUnion(edge.u, edge.v);
}
}
System.out.println(sum);
}- 손으로 그려본 최소 비용으로 형성 되는 트리는 21
- 실행 결과
U= 2 V= 7 W= 1
U= 1 V= 4 W= 2
U= 4 V= 7 W= 3
U= 1 V= 2 W= 4
U= 4 V= 5 W= 7
U= 2 V= 6 W= 8
U= 4 V= 2 W= 12
21
