머신 러닝 교과서 with 파이썬 2-2장

2.3 적응형 선형 뉴런과 학습의 수렴

Perceptron vs. Adaptive Linear Neuron (Adaline)

Perceptron은 결정함수를 통과한 y'을 사용해서 가중치를 업데이트 하는데 사용
Adaline은 결정함수, 즉 임계함수를 통과하기 전의 출력값을 사용하여 가중치를 업데이트 한다는 것이 특징. 또 최종 인풋을 그대로 사용하는 것이 아닌 활성함수를 통과. 이 때 활성함수는 항등함수로, 그대로 입력값을 그대로 출력함. (역할이 없는 것 같지만 로지스틱 회귀나 여타 알고리즘 구조에서 모종의 역할을 하게 된다고!!)

Perceptron이 상징적이기는 하지만 요즘 인공 신경망은 Adaline에 가까움.

2.3.1 경사 하강법으로 비용 함수 최소화

목적함수 == 비용함수(cost func) == 손실함수(loss func)

• 목적함수는 최적화 할 대상을 의미
• 비용함수는 손실을 모아서 전체 샘플에 대한 손실값을 판단하는 함수를 의미
• 손실함수는 샘플 하나에 대한 손실값을 의미
• 경사하강법은 비용함수와 손실함수 용어를 주로 사용

경사하강법에서 사용하는 손실함수는 '제곱오차합' (Sum Of Squared Errors)

손실함수 J 정의

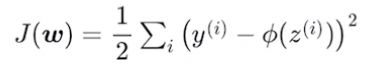
손실함수 J를 w_j에 대해서 평미분

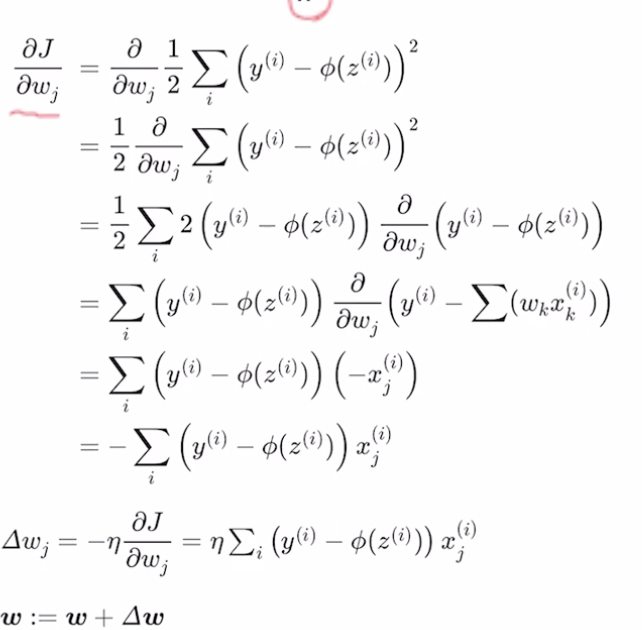
가중치가 하나인 경우 가장 최저점

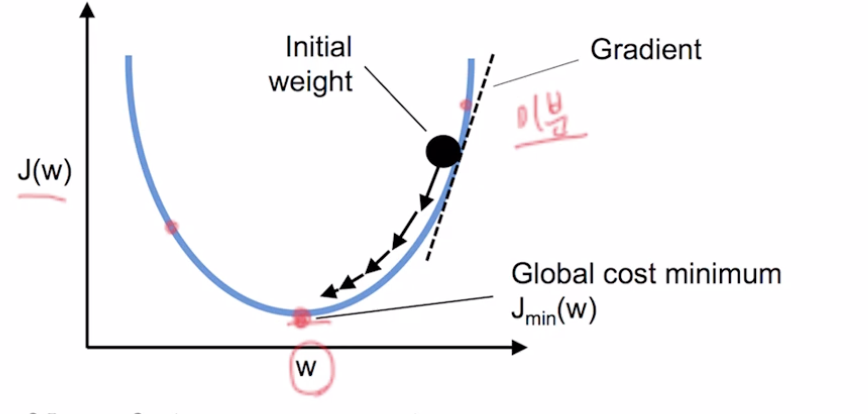
• 이 기울기(=경사, =기울기, =gradient, =평미분 값이) 점점 작아지는 방향이 지향점임.

2.3.2 파이썬으로 아달린 구현하기

class AdalineGD(object):
    """적응형 선형 뉴런 분류기

    매개변수
    ------------
    eta : float
      학습률 (0.0과 1.0 사이)
    n_iter : int
      훈련 데이터셋 반복 횟수
    random_state : int
      가중치 무작위 초기화를 위한 난수 생성기 시드

    속성
    -----------
    w_ : 1d-array
      학습된 가중치
    cost_ : list
      에포크마다 누적된 비용 함수의 제곱합

    """
    #이전과 마찬가지로 eta와 n_iter(반복 횟수) 지정.
    #그리고 random_state를 주어서 모델을 훈련해서 출력한 결과와 동일해지도록 했음
    def __init__(self, eta=0.01, n_iter=50, random_state=1):
        self.eta = eta
        self.n_iter = n_iter
        self.random_state = random_state

    def fit(self, X, y):
        """훈련 데이터 학습

        매개변수
        ----------
        X : {array-like}, shape = [n_samples(샘플의 갯수), n_features(특성)] 인 2차원 배열
          n_samples 개의 샘플과 n_features 개의 특성으로 이루어진 훈련 데이터
        y : array-like, shape = [n_samples] 인 1차원 배열
          타깃값

        반환값
        -------
        self : object

        """
        rgen = np.random.RandomState(self.random_state)
        self.w_ = rgen.normal(loc=0.0, scale=0.01, size=1 + X.shape[1])
        self.cost_ = []

        for i in range(self.n_iter):
            net_input = self.net_input(X)
            # Please note that the "activation" method has no effect
            # in the code since it is simply an identity function. We
            # could write `output = self.net_input(X)` directly instead.
            # The purpose of the activation is more conceptual, i.e.,  
            # in the case of logistic regression (as we will see later), 
            # we could change it to
            # a sigmoid function to implement a logistic regression classifier.
            
            #아래 작성된 net_input함수를 적용
            #activation 함수는 항등함수 (입력값을 바로 리턴) 
            output = self.activation(net_input)
            #이 에러 변수에는 모든 샘플에 대한 오차값이 담기게 됨
            errors = (y - output)
            #이 오차를 다시 X.T(전치 행렬)와 점곱 시행
            #이 전체 루프 안에서 가중치를 업데이트 하는 구문은 딱 한번
            self.w_[1:] += self.eta * X.T.dot(errors)
            #w_0는 절편
            self.w_[0] += self.eta * errors.sum()
            cost = (errors**2).sum() / 2.0
            self.cost_.append(cost)
        return self

	# 샘플X특성으로 구성된 2차원 배열 X와 특성의 개수만큼의 1차원 가중치 배열 W를 점곱을 하면 각 샘플마다 점곱이 이루어지게 됨. 샘플의 갯수만큼 결과가 만들어짐.
    # 그리고 샘플 개수의 절편(w0)을 다 더하면 모든 원소의 절편이 더해짐. (?) '브로드캐스팅' 이라고 함
    def net_input(self, X):
        """최종 입력 계산"""
        return np.dot(X, self.w_[1:]) + self.w_[0]

    def activation(self, X):
        """선형 활성화 계산"""
        return X

    def predict(self, X):
        """단위 계단 함수를 사용하여 클래스 레이블을 반환합니다"""
        return np.where(self.activation(self.net_input(X)) >= 0.0, 1, -1)

fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(10, 4))

ada1 = AdalineGD(n_iter=10, eta=0.01).fit(X, y)
ax[0].plot(range(1, len(ada1.cost_) + 1), np.log10(ada1.cost_), marker='o')
ax[0].set_xlabel('Epochs')
ax[0].set_ylabel('log(Sum-squared-error)')
ax[0].set_title('Adaline - Learning rate 0.01')

ada2 = AdalineGD(n_iter=10, eta=0.0001).fit(X, y)
ax[1].plot(range(1, len(ada2.cost_) + 1), ada2.cost_, marker='o')
ax[1].set_xlabel('Epochs')
ax[1].set_ylabel('Sum-squared-error')
ax[1].set_title('Adaline - Learning rate 0.0001')

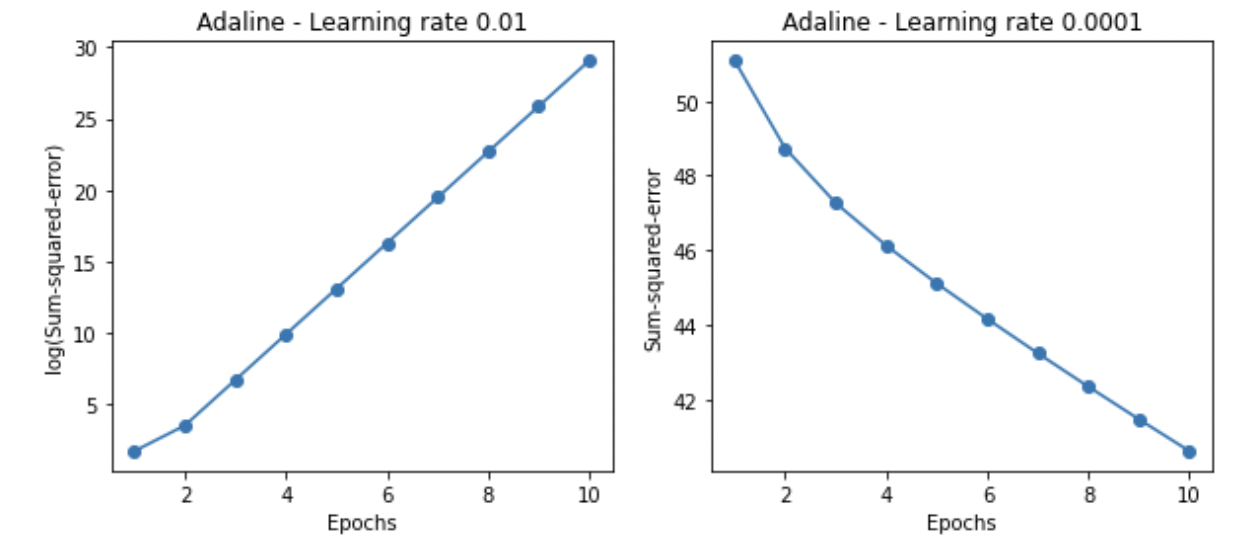
plt.show()

(왼) 에포크가 늘어남에 따라서 손실값이 늘어나는 것을 볼 수 있음
(오) 학습률을 0.0001로 설정했더니 손실값이 줄어드는 것을 볼 수 있음

좋은 하이퍼 파라미터를 찾아가는 과정이 중요.
하이퍼 파라미터란, 모델링 할 때 사용자가 직접 세팅해 주는 값으로 학습률(learning rate)나 서포트 벡터 머신에서의 C, sigma 값, KNN에서의 K값 등이 있다고 한다.

2.3.3 특성 스케일을 조정하여 경사 하강법 결과 향상시키기

특성값의 스케일이 많이 다르면 가중치의 업데이트가 공정하게 이루어지지 못함
=> 표준화를 통해 특성값의 스케일 조정
통계의 연속이군,,?

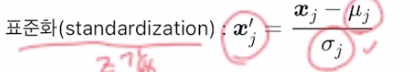
# 특성을 표준화합니다.
X_std = np.copy(X)
X_std[:, 0] = (X[:, 0] - X[:, 0].mean()) / X[:, 0].std()
X_std[:, 1] = (X[:, 1] - X[:, 1].mean()) / X[:, 1].std()

ada = AdalineGD(n_iter=15, eta=0.01)
ada.fit(X_std, y)

plot_decision_regions(X_std, y, classifier=ada)
plt.title('Adaline - Gradient Descent')
plt.xlabel('sepal length [standardized]')
plt.ylabel('petal length [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()

plt.plot(range(1, len(ada.cost_) + 1), ada.cost_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Sum-squared-error')

plt.tight_layout()
plt.show()