---

Abstract

최근 다양한 머신러닝의 영역에서 sota의 성능을 내는 방법들은 거대한 데이터셋을 사용하는 것에 달려있고, 데이터셋을 저장하는 것과 모델을 훈련하는 것이 상당히 비싸지고 있다(Computational Resource, Memory Resource가 많이 필요하게 됨). 이 논문에서는 data-efficient한 학습을 위해, 트레이닝셋 데이터를 합성하는 Data Condensation 방법을 소개한다. Data Condensation(DC)은 대규모 데이터셋을, 심층 신경망을 처음부터 학습하기 위한 informative한 작은 합성 샘플로 만드는 방법을 배운다. 우리는 원래 방식대로 훈련된 심층 신경망의 gradients와 합성 데이터의 gradient를 매칭하는 방법으로 이 방법을 공식화 했다. DC의 퍼포먼스를 여러 컴퓨터 비전 Benchmark로 엄격히 평가했고, sota보다 더 좋은 성능을 보여줬다. 마지막으로 Continual learning과 Neural Architecture Search(NAS)에서 DC를 적용하였다. 그리고 제한된 컴퓨터 메모리를 사용할 때와, 제한된 계산 환경에서 DC가 사용될 때 유용함을 발견했다.

1. Introduction

computer vision, natural language processing, speech recognition등의 여러 필드에서 sota의 성능을 가지는 머신러닝 모델을 얻기 위해, 일반적으로 수백만의 샘플을 포함하는 Large-scale datasets이 사용된다. 이러한 규모에서는, 데이터를 저장하고 전처리 하는것 조차 부담스럽고, 이를 기반으로 모델을 교육하는데는 전문 장비와 인프라가 필요하다. 대형 데이터를 다루는데 효과적인 한 방법은 data selection이다. data selection은 머신러닝 기술의 데이터 효율성 향상을 목표로 하는 가장 대표적인 샘플을(representative samples) 선별한다. 클래식한 data-selection 방법으로 알려져 있는 coreset construction은, 클러스터링 문제에 집중을 한다. coreset construction 방법은 최근엔 각각 훈련 샘플을 저장하고 레이블링 하는데 고정된 budget이 있는 Continual learning과 Active learning에서 찾을 수 있다. 이러한 방법은 일반적으로 대표성(representativeness), 다양성(diversity), 건망성(forgetfulness)에 대한 기준을 정의한 다음, 기준에 따라 대표 샘플을 선택한다. 마지막으로 선택된 소규모 데이터셋을 사용하여 downstream task에 사용한다.

불행히도, 이러한 방법들은 두가지의 단점이 있다: 첫 째로, 위의 방법들은 전형적으로 heuristics한 방법들을 사용하고(클러스터링의 가운데 표본을 취하는 방법) 그것은 downstream task에서 최적의 솔루션(optimal solution)을 보장하지 못한다. 둘 째로, 대표적인 샘플이 존재할 것이라는 보장이 없다는 점이다. 최근에 사용되는 방법인 Dataset Distillation(DD)은 large training data로부터 나온 informative한 small set을 학습하여 이러한 한계들을 넘어서고 있다. 특히 저자는 network parameter를 합성 훈련 데이터의 함수로 모델링하고, 합성 데이터에 대해 원래 훈련 데이터에 대한 training loss를 최소화 하는 방향으로 학습한다. coreset 방법과 다르게, 합성된 데이터는 downstream task에 직접적으로 최적화 될 수 있고, 그에 따라 이 방법은 대표적인 샘플의 존재유무에 의존하지 않는다.

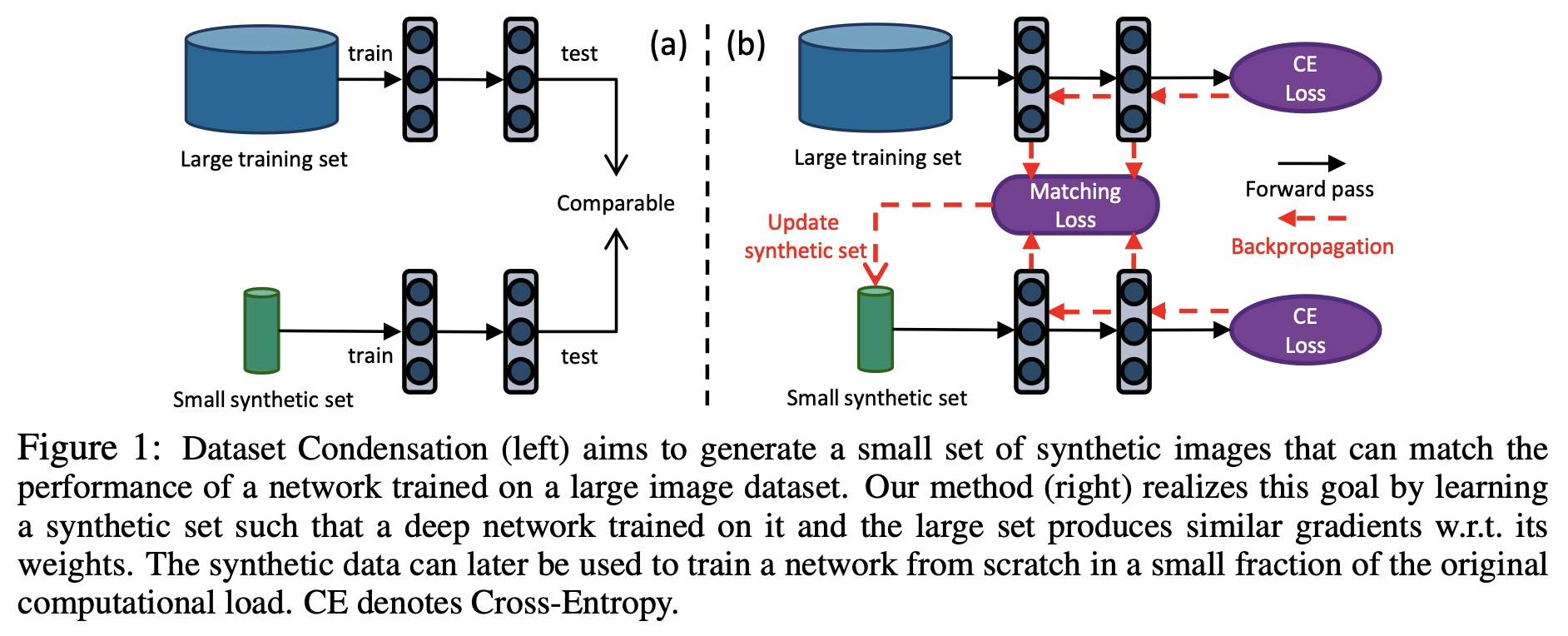
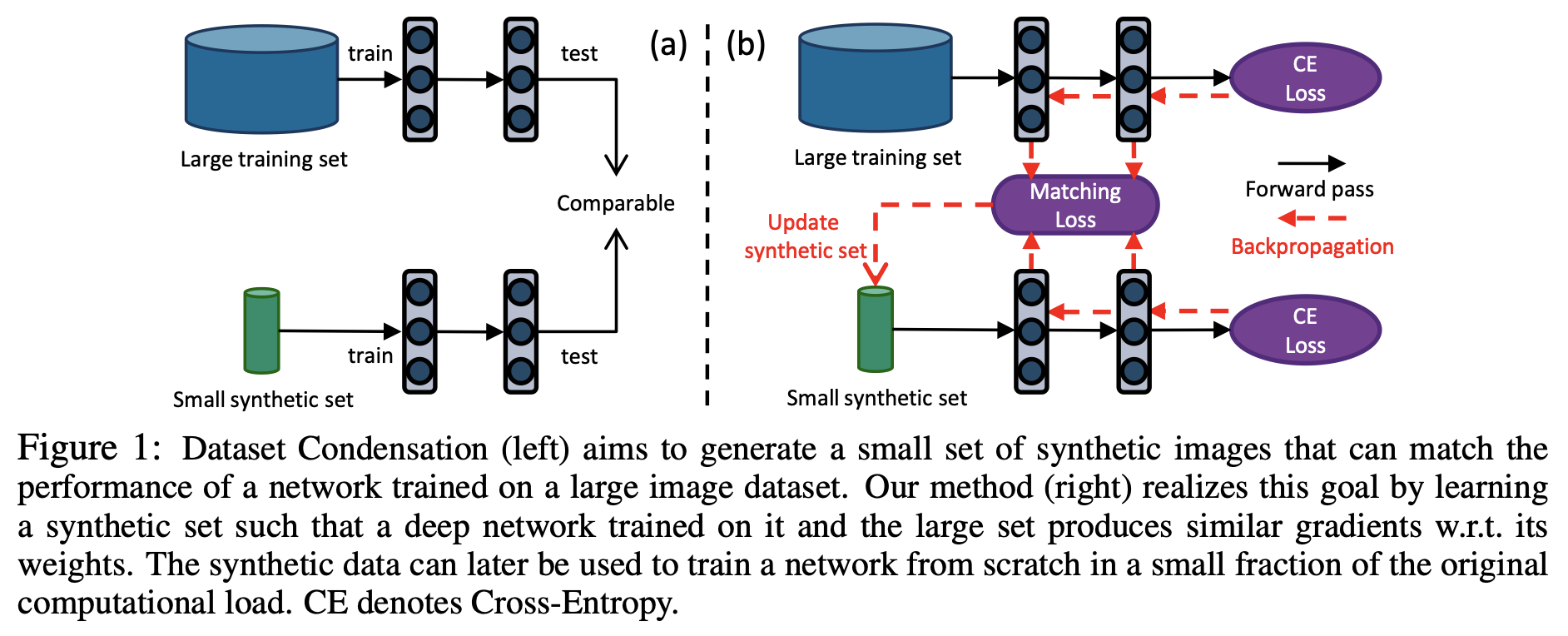
DD의 영향을 받아, 저자는 원본 데이터셋의 개별 샘플에 국한되지 않고 downstream task를 위해 신경망을 훈련하는데 최적화된 informative한 샘플들을 합성하는 방법을 배우는데 집중한다. DD와 같이 저자의 목표는 small set에 대해서 훈련된 synthesize 모델을 가지고 원본 데이터셋에서 훈련된 모델과 견줄 수 있을만한 최고의 일반화 성능을 내는 것이다(이상적으로). 특별히 우리는 다음 질문들에 대해서 연구하였다. 첫 번째는 큰 이미지 분류 데이터셋을 작은 합성 셋으로 압축할 수 있는가? 두 번째는 합성 셋으로 훈련된 이미지 분류 모델이 실제로 이미지를 분류할 수 있는가? 세 번째는 다른 신경망 구조를 훈련하는 데 사용할 수 있는 단일 합성 이미지셋을 만들 수 있는가? 이를 위해 우리는 심층 신경망이 작은 "농축된" 합성 샘플 셋을 합성하는 방법을 학습하는 Dataset Condensation 방법을 제안한다. DC는 큰 데이터셋에 대해서 훈련된 모델과 성능이 비슷할 뿐만 아니라,큰 데이터셋의 network parameter space와 가까운 solution을 얻어낼 수 있다. 우리는 이 목표를 큰 고정 훈련 셋과 학습 가능한 압축 셋에 대한 training loss에 대해 계산된 두 개의 network parameter gradients 사이를 최소화하는 것으로 공식화했다. 위에서 제안한 방법은 합성 이미지들을 이용한 효율적인 학습이 가능하다는 것과, 그것으로 신경망 학습이 가능하다는 것을 보여준다. 또한 여러 컴퓨터 비전 Benchmarks에서 넓은 마진으로 coreset 방법을 능가한다. 추가로 compact한 합성 샴플로 훈련하는 것은 훈련 이미지에 대해서 fixed budget이 있는 다른 학습문제에 적용했을 때 유용하다. 우리는 이 논문에서 제안한 방법이 Continual learning에서 지속적으로 more informative한 훈련 샘플들을 제공함으로써 인기있는 data selection 방법을 능가함을 보여준다. 마지막으로 Neural Architecture Search(NAS)에서 DC의 유망한 사용 사례를 탐색하고 농축된 이미지가 학습되면, 수 많은 네트워크 구조를 매우 효율적으로 훈련하는데 사용할 수 있음을 보여준다.

우리의 방법은 앙상블 모델의 지식을 단일 모델로 이전하는 Knowledge Distillation(KD) 방법과 연관이 있다. KD와는 다르게, 우리는 큰 훈련 세트에 대한 지식을 작은 합성 셋으로 증류(distill)한다. 또한 우리의 방법은 Generative Adversarial Networks(GAN)와 Variational AutoEncoders가 데이터 분포를 캡쳐하여 충성도가 높은 샘플을 합성한다는 점에서 연관이 있다. 반면에 우리의 목표는 "실제처럼 보이는" 샘플을 생성하는 것이 아니라, 심층 신경망 훈련을 위한 informative samples를 생성하는 것이다. 마지막으로 우리의 방법은 feature activation을 입력 픽셀 공간으로 다시 투영하여 이미지 패치를 생성하는 방법과, feature activation을 matching하여 input 이미지를 재구성하는 방법, 주어진 training gradients를 통한 private training 이미지를 복구하는 방법, zero-shot learning을 위한 semantic embeddings으로 부터의 feature 합성하는 방법들과 관련이 있다. 그러나 우리의 목표는 원본 복구 및 누락된 이미지를 복구하기 위해서 압축된 훈련 이미지셋을 합성하는 것은 아니다.

2. Method

2.1 Dataset Condensation

훈련용 이미지와 클래스 레이블이 쌍으로 이루어져 있는 large dataset $|\mathcal{T}|$ 가 주어졌다고 가정하자. $\mathcal{T} = \{ (x_i,y_i) \} |_{i=1}^{| \mathcal{T}|}$ 이고 $x \in \mathcal{X} \subset \mathbb{R}^d, y \in \{ 0,...,C-1 \}$, 여기서 $\mathcal{X}$는 d-차원 입력 공간이고, $C$는 클래스의 개수이다. 우리는 미분 가능한 함수 $\phi$(심층 신경망)에 대해서 이전에 본 적이 없는 이미지의 label을 정확하게 예측하는 $\theta$ 파라미터에 대해서 학습하기 원한다(즉 $y=\phi_\theta(x)$). 이 함수의 매개변수를 학습하는 한 방법은, 전체 훈련 세트에 걸쳐 경험적 loss term을 최소화하는 것이다.

$\mathcal{L}^\mathcal{T}(\theta) = \frac{1}{|\mathcal{T}|} \sum_{(x,y) \in \mathcal{T}} \ell(\phi_\theta(x),y)$ 이고, $\ell(\cdot,\cdot)$은 task 특정 손실함수이다(cross-entropy 같은). 그리고 $\theta^\mathcal{T}$는 $\mathcal{L}^\mathcal{T}$의 최소값이다. 모델 $\phi_{\theta^\mathcal{T}}$ 으로부터 얻어진 성능의 일반화 공식은 데이터 분포가 $P_\mathcal{D}$일 때, $\mathbb{E}_{x \sim P_{\mathcal{D}}}[\ell(\phi_{\theta^\mathcal{T}}(x),y)]$과 같이 쓰인다. 우리의 목표는 응축되어 합성된 샘플들과 그들의 레이블을 가지는 작은 데이터셋을 만드는 것이다. $\mathcal{S} = \{(s_i,y_i) \}|_{i=1}^{|\mathcal{S}|}$ 일때, $s \in \mathbb{R}^d$ 이고 $y \in \mathcal{Y}$, 그리고 $|\mathcal{S}| \ll |\mathcal{T}|$ 이다. 식(1)과 비슷하게, 응축된 셋이 학습되면 다음식을 통해 $\phi$ 를 훈련시킬 수 있다.

$\mathcal{L}^\mathcal{S}(\theta) = \frac{1}{|\mathcal{S}|}\sum_{(s,y) \in \mathcal{S}}\ell(\phi_\theta(s),y)$이고, $\theta^\mathcal{S}$는 $\mathcal{L}^\mathcal{S}$의 최소값이다. 합성셋 $\mathcal{S}$는 원본 데이터셋에 비해 2-3차수 만큼 상당히 작다. 우리는 식(1)보다 상당히 빠르게 하기 위해서 식(2)에서는 최적화를 생략했다. 우리는 또한 일반화 성능 $\phi_{\theta^\mathcal{S}}$ 가 $\phi_{\theta^\mathcal{T}}$와 실제 데이터 분포 $P_\mathcal{D}$에 걸쳐서 비슷한 성능을 내기를 원한다. 즉 $\mathbb{E}_{x \sim P_\mathcal{D}}[\ell(\phi_{\theta^\mathcal{T}}(x),y)] \simeq \mathbb{E}_{x \sim P_\mathcal{D}}[\ell \phi_{\theta^\mathcal{S}}(x),y)]$ 가 실제 데이터 분포 $P_\mathcal{D}$에 걸친 결과이다.

Discussion 응축된 데이터로 훈련되어 원본 데이터로 훈련된 모델과 비교할만한 일반화 성능을 가지도록 하는 목표는, 여러 방식으로 공식화 될 수 있다. 한 접근 방식은, 파라미터 $\theta^\mathcal{S}$를 합성 데이터 $\mathcal{S}$의 함수로 투영하는 것이다 :

우리의 방법은 $\mathcal{S}^*$에 대해 훈련된 모델 $\phi_{\theta^\mathcal{S}}$가 원본 데이터에 대해서도 training loss를 최소화 하도록 하는 최적의 합성 이미지셋 $\mathcal{S}^*$를 찾는것이 목표이다. 식(3)을 최적화 하는 것은 중첩된 최적화 루프를 포함하며, $\mathcal{S}$의 gradient를 복구하기 위해 각 iter마다 inner loop를 푸는 것은 계산적으로 비싼 과정이다. 그러므로, 큰 모델로는 확장되지 않고 또한 inner-loop optimizer가 많은 단계를 가지면 정확하지 않다. 다음으로 우리는 Dataset Condesation을 위한 대안의 공식을 제안한다.

2.2 Dataset Condensation with Parameter Matching

여기서 우리는 모델 $\phi_{\theta^\mathcal{S}}$가 $\phi_{\theta^\mathcal{T}}$에 필적하는 일반화 성능을 달성할 뿐만 아니라 매개변수 공간에서 유사한 solution으로 수렴하도록 $\mathcal{S}$를 학습하는 것을 목표로 한다($\theta^\mathcal{S} \ \approx \ \theta^\mathcal{T}$). $\phi_\theta$를 locally smooth function이라고 두자, 비슷한 가중치($\theta^\mathcal{S} \ \approx \ \theta^\mathcal{T}$)는 파라미터 공간에서 local neighborhood하게 비슷한 맵핑을 할 것이고, 그것의 일반화 성능 또한 비슷할 것이다. ($\mathbb{E}_{x \sim P_\mathcal{D}}[\ell(\phi_{\theta^\mathcal{T}}(x),y)] \simeq \mathbb{E}_{x \sim P_\mathcal{D}}[\ell \phi_{\theta^\mathcal{S}}(x),y)]$) 이제 우리는 이 목표를 다음과 같이 공식화 할 수 있다.

$\theta^\mathcal{T} = \underset{\theta}{\arg \min} \ \mathcal{L}^\mathcal{T}(\theta)$ 이고 $D(\cdot,\cdot)$ 는 거리 함수이다. 심층 신경망에서, $\theta^\mathcal{T}$는 전형적으로 초기화 값인 $\theta_0$에 달려있다. 반면에, 식(4)에서의 최적화는 $\theta_0$로 초기화된 모델 $\phi_{\theta^\mathcal{T}}$의 최적의 합성 이미지셋만을 얻는 것이 목표이다. 우리의 실제 목표는 어떠한 랜덤 초기값의 분포 $P_{\theta_0}$에서든지 동작하는 샘플을 만드는 것이다. 그러므로 우리는 식(4)를 다음과 같이 수정한다.

$\theta^\mathcal{T} = \underset{\theta}{\arg \min} \ \mathcal{L}^\mathcal{S}(\theta(\theta_0))$이다. 간결성을 위해 각각 $\theta^\mathcal{S}(\theta_0)$, $\theta^\mathcal{T}(\theta_0)$ 대신 $\theta^\mathcal{S}$와 $\theta^\mathcal{T}$만 사용한다. 식(5)를 해결하는 기본적인 접근방법은 음함수의 미분법을 사용하는 것이다. 이는 $\theta^\mathcal{S}$를 위한 inner loop optimization을 포함한다. inner loop optimization $\theta^\mathcal{S}(\mathcal{S}) = \underset{\theta}{\arg \min} \ \mathcal{L}^\mathcal{S}(\theta)$는 큰 모델의 경우 계산적으로 비싸다, 하지만 back-optimization을 접근법을 사용해 $\theta^\mathcal{S}$를 다음과 같이 incomplete optimization의 결과를 내도록 재정의하면 해결될 수 있다.

$\mathrm{opt-alg}$은 고정된 수($\zeta$)의 단계를 밟는 특정한 최적화 절차이다.
실제로, $\theta^\mathcal{T}$를 위한 다른 초기값들은 오프라인 상태에서 먼저 학습된 뒤에 식(5)에서 타겟 파라미터 벡터로 사용될 수 있다. 하지만, $\theta^\mathcal{T}$를 타겟 벡터로 회귀하는 방법을 학습하는데에는 두 가지 잠재적인 문제가 있다. 첫 번째는, $\theta^\mathcal{T}$와 그것과 인접한 값인 $\theta^\mathcal{S}$ 사이의 거리가, 파라미터 공간상에서 둘의 경로 사이에 많은 local minima trap이 있을 경우에 너무 커져서 도달하기 힘들다는 것이다. 두 번째로는 $\mathrm{opt-alg}$가 속도와 정확도의 trade-off 로 정해진 한정된 수의 단계만을 최적화 하기 때문에 optimal solution에 이르는데 충분하지 않을 수 있다는 점이다.

2.3 Dataset Condensation with Curriculum Gradient Matching

우리는 위에서 언급된 문제들을 다루기 위해 커리큘럼 기반의 접근법을 제시한다. 핵심 아이디어는 $\theta^\mathcal{S}$가 $\theta^\mathcal{T}$에 근접할 뿐만이 아니라, 최적화의 전반에 걸쳐 $\theta^\mathcal{T}$와 비슷한 경로를 따르는 것이다. 이것은 $\theta$에 대한 최적화 dynamics를 제한할 수 있지만, 더 잘 가이드된 최적화를 가능하게 하고 incomplete optimizer의 효과적인 사용을 가능하게 함을 볼 수 있다. 우리는 이제 위에서 제시된 식(5)를 여러 하위 식으로 분해할 수 있다.

$T$는 iteration의 횟수 이고, $\zeta^\mathcal{S}$ 와 $\zeta^\mathcal{T}$는 각각 $\theta^\mathcal{S}$와 $\theta^\mathcal{T}$의 최적화 단계의 횟수이다. 한마디로, 우리의 희망사항은 각 반복 $t$마다 생성된 응축 샘플 $\mathcal{S}$로 훈련된 네트워크 파라미터 $\theta^\mathcal{S}_t$가 원본 데이터로 훈련된 $\theta^\mathcal{T}_t$와 비슷하도록 만드는 샘플 $\mathcal{S}$를 생성해내는 것이다. 우리의 사전 학습으로 $\mathcal{S}$로 매개변수화 되는 $\theta^\mathcal{S}_{t+1}$가 $\mathcal{S}$를 $D(\theta^\mathcal{S}_t,\theta^\mathcal{T}_t)$가 0에 가까워지게끔 업데이트 함으로써 $\theta^\mathcal{T}_{t+1}$로 성공적으로 추적될 수 있음을 관찰했다.

$\mathrm{opt-alg}$에 대한 1단계 경사 하강법 최적화의 경우 업데이트 규칙은 다음과 같다:

여기서$\eta_\theta$는 학습률이다. 우리의 관찰 $D(\theta^\mathcal{S}_t, \theta^\mathcal{T}_t) \approx 0$ 에 기초하여, 식(7)은 다음과 같이 간단하게 쓸 수 있다.

이제 우리는 합성 셋 $\mathcal{S}$에 대해서 학습된 파라미터 $\theta$를 가지고 있는 단일 심층 신경망을 얻게 되었다. 이 합성 셋 $\mathcal{S}$는 $\theta$에 대한 $\mathcal{L}^\mathcal{T}$의 샘플의 전반적인 손실에 대한 기울기와, $\theta$에 대한 $\mathcal{L}^\mathcal{S}$의 응축된 샘플의 전반적인 손실에 대한 기울기의 거리를 최소화 하는 방향으로 최적화 되어있다. 다시 말하면, 우리의 목표는 응축 샘플 업데이트를 통해, $\theta$에 대해서 real training loss 그리고 synthetic training loss에 대한 gradient를 일치시키는 것으로 축소된다. 이러한 근사는 이전 매개변수에 대한 재귀 계산 그래프의 값비싼 unrolling이 필요하지 않다는 점이 주요한 이점이 된다. 중요한 결과는 최적화가 훨씬 더 빠르고 메모리 효율적이어서 최첨단 심층 신경망으로 확장될 수 있다는 점이다.

Discussion 합성 데이터에는 샘플뿐만 아니라 최적화를 통해 공동으로 학습할 수 있는 레이블$(s, y)$도 이론적으로 포함된다. 그러나 샘플의 내용이 레이블에 따라 다르고 그 반대의 경우도 마찬가지이므로 공동 최적화가 어렵다. 따라서 실험에서는 고정 레이블에 대한 이미지를 합성하는 방법을 배운다. (예: 클래스당 하나의 합성 이미지)

Algorithm. 우리는 최적화 세부사항을 알고리즘 1 으로 그렸다. outer level에서는 임의 가중치 초기화에 대한 루프를 포함하는데, 이전에 보지 못한 모델을 훈련하는 데 나중에 사용할 수 있는 압축된 이미지를 얻기 위한 초기화이다. 먼저 $\theta$가 무작위로 초기화되면, $\phi_\theta$를 사용하여 트레이닝 샘플($\mathcal{L}^\mathcal{T}$)와 합성 샘플($\mathcal{L}^\mathcal{S}$)의 loss 및 $\theta$에 대한 gradient를 계산한다. 그런 뒤 gradient descent steps($\zeta_\mathcal{S}$)와 learning rate($\eta_\mathcal{S}$)가 적용된 gradient matching을 통해 합성 샘플 $\mathcal{S}$를 최적화한다. 우리는 두 $\mathrm{opt-alg}$에 stochastic gradient descent optimization을 적용한다. 다음으로 우리는 loss($\mathcal{L}^\mathcal{S}$)를 최소화하는 방향으로 업데이트 된 합성 이미지로 learning rate($\eta_\mathcal{\theta}$)와 steps($\zeta_\mathcal{\theta}$)를 적용해 $\theta$를 훈련한다. 단일 클래스의 샘플을 포함하는 전체 $\mathcal{T}$ 및 $\mathcal{S}$에서 각 real 및 synthetic 배치 쌍을 샘플링 한다. 그리고 각 클래스에 대한 synthetic 데이터는 다음과 같은 이유로 각 반복($t$)에서 별도로(병렬적으로) 업데이트 된다. 첫 번째, 이 방법은 훈련할 때 메모리 사용을 줄인다. 두 번째, 단일 클래스의 데이터에 대한 평균 기울기를 모방하는 것이 여러 클래스의 데이터에 대한 평균 기울기를 모방하는 것에 비해 더 쉽다. 그리고 이것은 추가적인 계산 비용이 발생하지 않는다.

Grdient matching loss 식(9)에 나오는 matching loss $D(\cdot,\cdot)$는 $\theta$에 대한 $\mathcal{L}^\mathcal{S}$와 $\mathcal{L}^\mathcal{T}$사이의 기울기의 거리를 측정해준다. $\phi_\theta$가 다층의 신경망일때, 기울기는 각 완전연결(FC) 및 컨볼루션 레이어에 대해 학습 가능한 2D($\mathrm{out} \times \mathrm{in}$) 및 4D($\mathrm{out} \times \mathrm{in} \times \mathrm{h} \times \mathrm{w}$)가중치 세트에 해당한다. matching loss는 layerwise losses들을 합치는 것으로 분해될 수 있다.

$\mathrm{A}_{i \cdot}$, $\mathrm{B}_{i \cdot}$는 각각 node $i$에 대응하는 flattend vectors이다. FC 가중치에 대해서는 $\mathrm{in}$-차원이고 Convolutional 가중치에 대해서는 $\mathrm{in} \times \mathrm{h} \times \mathrm{w}$-차원이다. 모든 레이어에 대한 텐서를 하나의 벡터로 병합하고 두 벡터 사이의 거리를 계산하여 레이어별 구조를 무시하는 방법과는 다르게, 우리는 각 출력 노드에 대해서 그룹화 한다. 우리는 이 방법이 gradient matching에 더 좋은 거리계산 방법이며, 또한 모든 계층에서 하나의 학습률을 사용할 수 있는 방법임을 알아냈다.

3. Experiments

3.1 Dataset Condensation

먼저 우리는 응축된 이미지의 분류 성능을 측정하기 위해서 4개의 표준 benchmark 데이터셋: 숫자 인식을 위한 MNIST, SVHN, object classification을 위한 FashionMNIST, CIFAR10 을 사용한다. 우리는 6개의 표준 네트워크에 적용해서 테스트 하였다 : MLP, ConvNet, LeNet, AlexNet, Vgg-11, ResNet-18. MLP는 두 개의 비선형 은닉층을 가진 다층 퍼셉트론이며 각각 128개의 unit을 가진다. ConvNet은 $D$ 중복 블록을 사용하는 몇 번의 학습에서 일반적으로 사용되는 모듈식 아키텍쳐이다. 각 블럭은 $W (3 \times 3)$ 필터와, 일반화 층 $N$, 활성층 $A$, 풀링층의 $P$로 구성 되어있다. $[W,N,A,P] \times D$ 로 표기한다. 기본적인 ConvNet은 128개의 필터로 구성된 3개의 블럭과, InstanceNorm, ReLU, AvgPooling 모듈로 구성되어 있다. 마지막 블럭은 linear classifier를 따른다. 우리는 네트워크 가중치의 초기화를 위해 Kaiming initialization을 사용한다. synthetic images는 Gaussian noise나 무작위로 선택된 실제 이미지를 통해 초기화될 수 있다.

dataset condensation을 pipeline하기 위한 두 단계가 있다: condesed images를 배우는 것과, 분류기를 처음부터 학습하는 것이다. 두 단계에서 사용된 모델 아키텍쳐는 다를 수 있다. coreset baseline의 경우, coreset이 첫 단계에서 먼저 선택된다. 우리는 클래스당 1, 10, 50개의 이미지로 학습하는 3개의 세팅에 대해서 실험했다. 즉, 압축셋 또는 coreset에는 클래스당 각각 1, 10, 50개의 이미지가 포함된다. 각각의 방법마다 5번씩 실행했고 5개의 합성셋이 첫 단계에서 생성되었다. 생성된 각 합성셋은 두 번째 단계에서 무작위로 초기화된 20개의 모델을 훈련하는데 사용된다. 그리고 두 번째 단계에서 100개의 모델을 평가하는 테스트셋을 통해 성능이 평가된다. 모든 실험에서 이 100개의 테스트 결과에 대한 평균과 표준편차를 보고하였다.

Baselines 우리는 우리의 방법과 4개의 coreset baselines(Random, Herding, K-Center, Forgetting)을 비교했고, DD와도 비교하였다. Random 방법에서는, coreset으로 training samples가 무작위로 선택된다. Herding baseline은 cluster center에서 가장 가까운 샘플을 선택한다. K-Center는 데이터 점과 가장 가까운 중심 사이의 거리가 최소화되도록 여러 중심점을 선택한다. Herding 및 K-Center의 경우 전체 데이터셋에 대해 훈련된 모델을 사용하여 feature를 추출하고 중심까지의 $l_2$거리를 계산한다. Forgetting 방법은 훈련 과정에서 잊기 쉬운 training sample을 선택한다. 우리는 GSS-Greedy 방법은 비교하지 않았는데, 이는 K-Center 방법과 같은 유사성 기반 greedy 알고리즘이기 때문이다. GSS-Greedy는 온라인 학습 모델을 학습하여 샘플의 유사성을 측정하기 때문에 일반적인 이미지 분류 문제와 다르다.

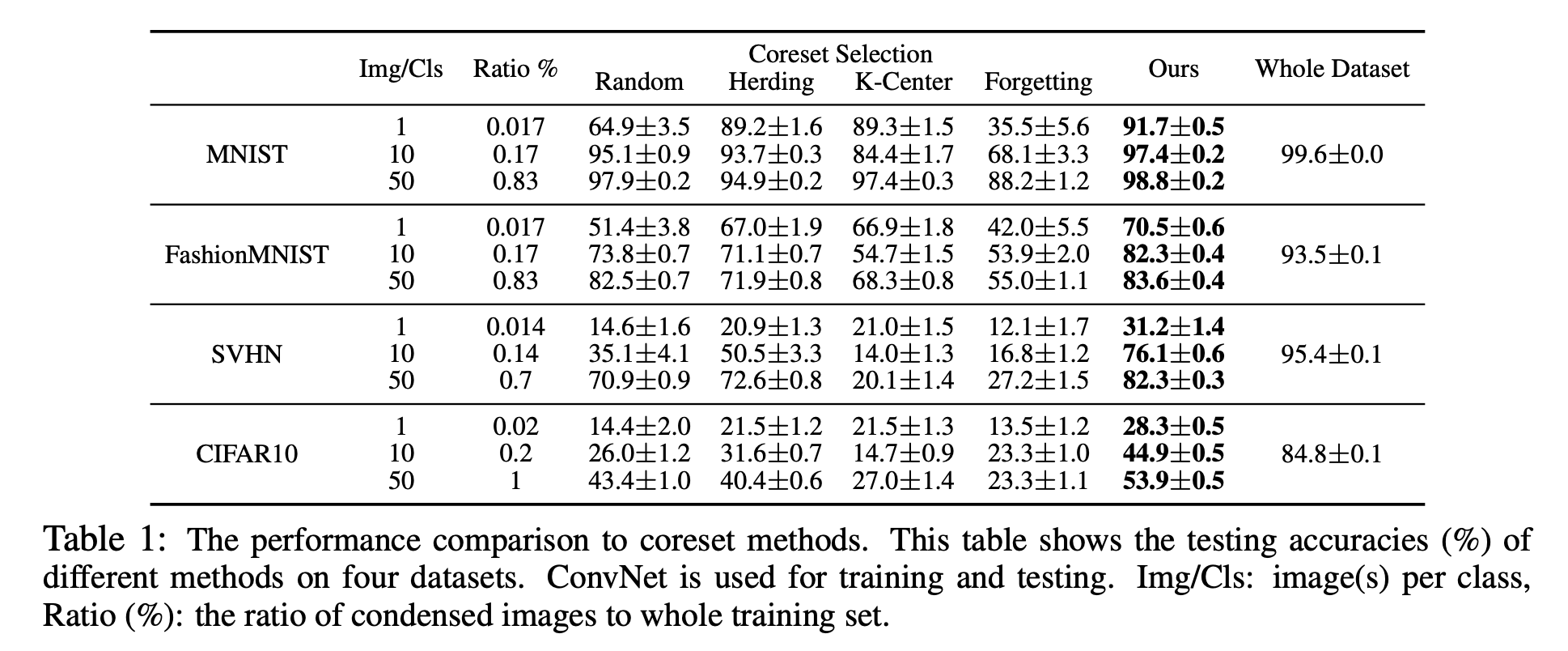
coreset 방법과의 비교. 처음으로 우리의 방법과 coreset baseline을 MNIST, FashionMNIST, SVHN, CIFAR10에 대해서 비교했다. 표1에 기본 ConvNet 모델을 사용한 분류 정확도를 표기하였다. Whole Dataset은 대략적인 상한 성능으로, 전체 원본 세트에 대해 훈련한 성능을 나타낸다. 먼저 우리의 방법이 MNIST에서 모든 baseline들의 성능을 뛰어넘는다는 것을 확인할 수 있다, 클래스당 50개의 이미지의 경우 원본 데이터의 개수(6000개)보다 2차수나 적은 데이터를 사용했음에도(50개) 전체 원본 이미지를 사용한 성능(upper bound)에 견줄만큼의 성능을 보여주었다. 또한 우리는 FashionMNIST에서 유망한 결과를 얻었지만, 다양한 전경과 배경을 가진 더 다양한 이미지를 포함하는 SVHN, CIFAR10에서 우리의 방법과 upper bound의 간극이 큼을 확인할 수 있다. 또한 우리는 random selection이 다른 baseline들과 클래스당 10 및 50개의 이미지를 가지는 조건을 비교했을 때 경쟁력이 있다는 것과, Herding 방법이 coreset 기법들 중 평균적인 성능이 가장 좋다는 것을 관찰했다. 우리는 1개의 이미지/클래스 조건에서 우리의 방법으로 만들어진 합성 이미지를 그림2에 시각화하였다. 흥미롭게도 시각화된 이미지는 눈으로 알아볼 수 있는 형태였고, 각 클래스의 "프로토타입"으로 보인다.

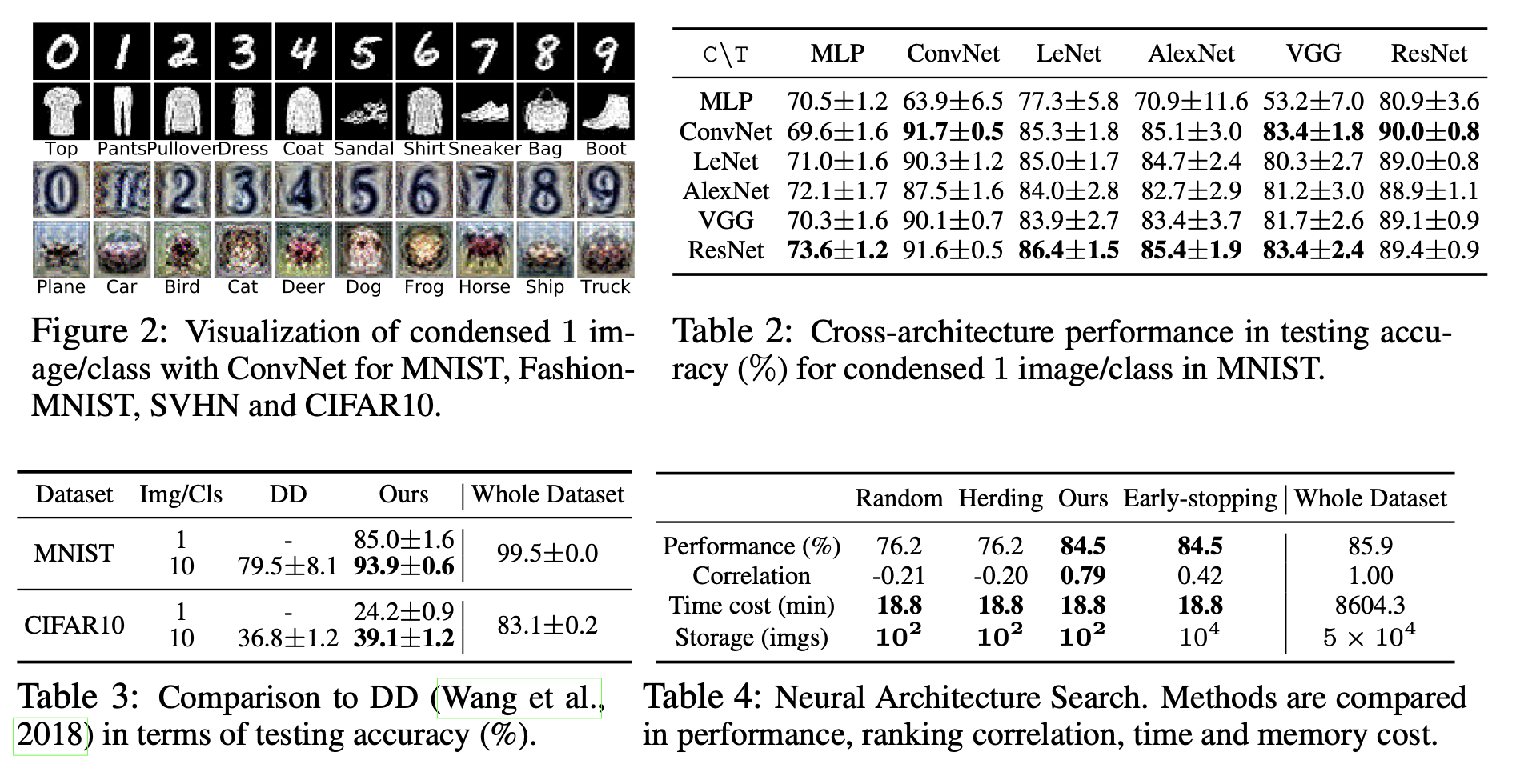
Dataset Distillation(DD)과의 비교. 표1의 세팅과는 다르게, DD는 클래스당 10개의 이미지의 조건으로 실험했고, MNIST, CIFAR10의 데이터셋과 LeNet, AlexCifarNet(커스텀 된 AlexNet)을 사용했다. 우리는 DD논문에서 제시되었던 방법을 그대로 따라서 실험을 진행하였다. 그 결과를 표3에 정리해 두었다. 우리의 방법은 두 벤치마크에서 DD의 성능을 상당히 앞섰다: DD가 클래스별 10개의 이미지를 적용해 얻은 결과보다 우리의 모델이 클래스별 1개의 이미지를 적용해서 얻은 결과가 5% 더 높았다. 추가로 우리의 방법은 MNIST에서 여러번의 실험에도 0.6%의 표준편차를 보이면서 지속적으로 좋은 결과를 보여준 반면, DD는 8.1%의 표준편차를 보이며 실행마다 다른 결과를 보여주었다. 마지막으로 우리의 방법은 CIFAR10 실험에서 DD에 비해서 2배 빠른 속도로 훈련할 수 있었고, 50% 더 적은 메모리를 사용하였다.

Cross-architecture generalization. 우리 방법의 또 다른 이점은 한 아키텍쳐를 사용하여 학습된 압축 이미지를 사용하여 본적 없는 다른 아키텍쳐를 훈련할 수 있다는 것이다. 클래스당 1개의 이미지를 가지는 condensed MNIST로 여러 네트워크(MLP, ConvNet, LeNet, AlexNet, VGG-11, ResNet-18)를 훈련한 내용이 표2에 정리 되어있다. 한 네트워크에 대해서 응축 셋이 합성되면(1이미지/1클래스), 그것을 다른 네트워크에서 처음부터 학습시켜 원본 MNIST 테스트 셋에 대해서 얼마나 정확하게 분류할 수 있는지를 평가한다. 표2는 condensed image, 특히 컨볼루션 네트워크로 훈련된 images가 좋은 성능을 내며, 아키텍쳐는 generic함을 보여준다. MLP로 만들어진 이미지는 컨볼루션 아키텍쳐를 훈련하는데 잘 동작하지 않는데, 이는 아마도 MLP와 Convolutional Network 사이의 translation invariance의 불일치 때문일 것이다. 흥미롭게도 MLP는 MLP에서 생성된 이미지를 쓸 때보다, 컨볼루션 네트워크를 통해 생성된 이미지를 쓸 때 더 좋은 성능을 달성했다. ResNet으로 생성된 이미지를 사용할 때와 ConvNet, ResNet을 분류기로 사용한 대부분의 경우, 원본 데이터로 훈련된 성능과 견줄만한 최고의 성능을 얻을 수 있었다.

Number of condesed images. 우리는 또한 MNIST, FashionMNIST, SVHN, CIFAR10에 대해서 ConvNet으로 훈련된 모델의 성능을 다양한 클래스당 이미지의 개수에 따라 평가했다. 그림3에 절대적인 정확도와 upper bound에 대한 상대적인 정확도가 나와있다. 응축된 이미지의 개수를 늘리는 것은 모든 벤치마크에서 성능 향상을 가져다 주었고, MNIST와 FashionMNIST의 경우 upper-bound 성능과의 차이가 매우 적었다. 반면에 SVHN, CIFAR10에서는 upper-bound와는 큰 차이가 있었다. 추가로 우리의 방법은 coreset 방법(Herding)의 성능을 큰 마진으로 앞섰다.

Activation, normalization & pooling 우리는 또한 다양한 활성화 함수(sigmoid, ReLU, leaky ReLU), pooling, 일반화 함수(batch, group, layer, instance norm)의 영향에 대해서도 연구하였다. 그리고 다음의 관찰을 얻었다: leaky ReLU가 ReLU보다 그리고 average pooling이 max pooling보다 응축된 이미지를 더 잘 학습하게 만들었는데, 이는 그들이 더 조밀한 기울기 흐름을 가능하게 하기 때문이다. 인스턴스 정규화는 압축된 이미지의 작은 데이터셋에 대해 훈련된 네트워크에서 사용될 때, 다른 방법들보다 더 좋은 분류 성능을 보여준다.

3.2 Applications

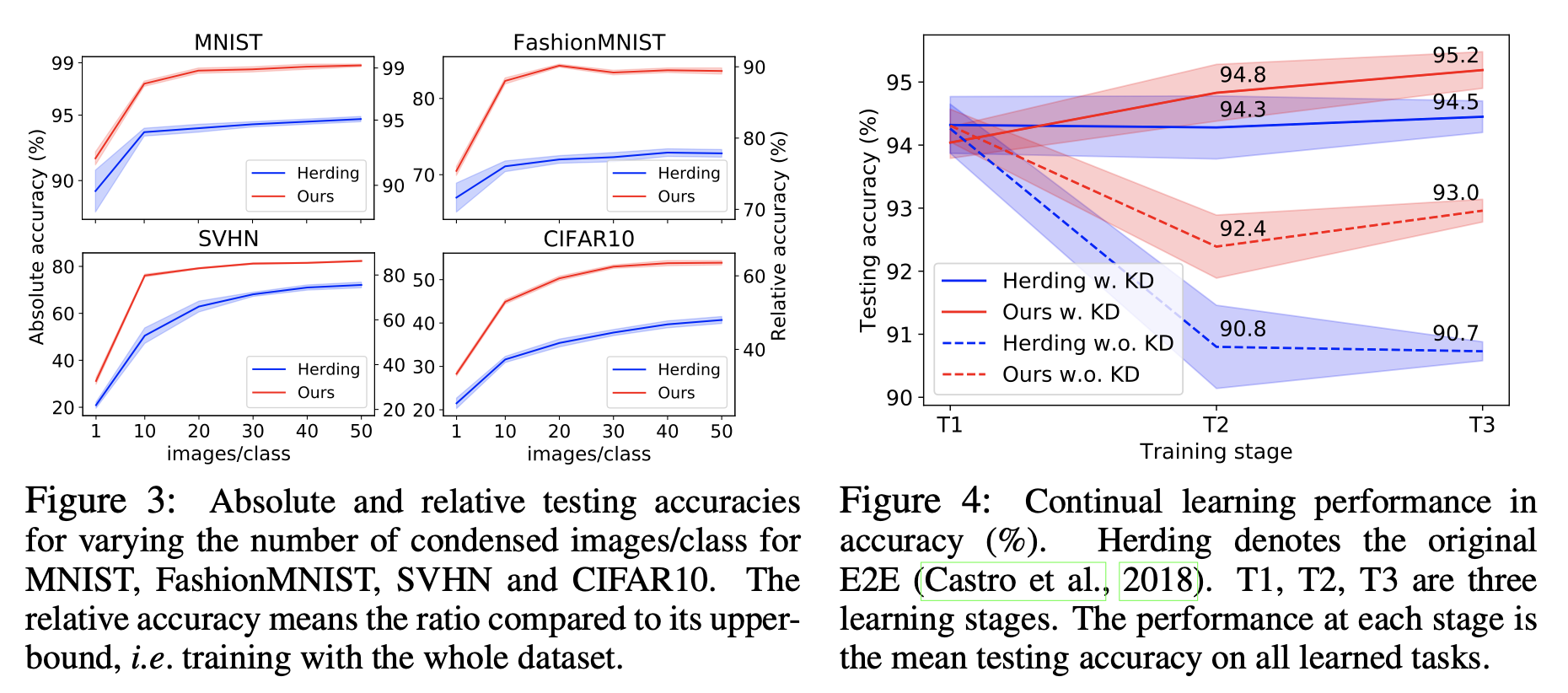
Continual Learning 먼저 우리의 방법을 continual learning senario에 적용하였다. continual learning은 목표는 새로운 task가 증가하여 기존 모델에 새로운 task에 대한 학습이 이루어져도 old task에 대한 성능을 유지하는 것이다. 우리는 제한된 rehearsal memory(여기서는 10 이미지/클래스)를 사용하는 E2E(End to End) 방법으로 continual learning 모델을 만들었다. rehearsal memory는 old task로 부터의 representative samples를 유지하고 이전의 네트워크 출력에 대해 정규화하는 Knowledge Distillation(KD)를 위해 사용된다. 우리는 Continual Learning의 샘플 선택 메커니즘(herding)을 응축된 이미지세트를 생성하여 메모리에 저장하는 방법(DC)으로 바꾸었다. 모델의 나머지 부분은 그대로 남겨놓고, SVHN, MNIST, USPS 데이터를 사용하여 숫자를 인식하는 task-incremental learning problem에 적용하였다. MNIST와 USPS는 $32 \times 32$ RGB 이미지로 reshape 하였다.

우리의 방법과 E2E(herding) 방법을 비교한 것이 그림 4에 나와있다. KD regularization을 포함하는 것과 포함하지 않는 것을 나누었다. 실험에는 3개의 증가하는 학습 단계가(SVHN -> MNIST -> USPS) 포함되며, 테스트 정확도는 각 단계 별로 전체 테스트셋에 대한 과거의 task와 현재의 task를 평균함으로 계산된다. 원하는 결과는 T3에서 높은 분류 정확도를 얻는 것이다. 결과적으로 응축된 이미지가 herding으로 샘플된 것보다 더 data-efficient하고, 두 세팅 모두에서 우리의 방법이 E2E 방법을 뛰어 넘었다(KD를 사용하지 않았을 경우 T3 에서 2.3%의 큰 마진으로).

Neural Architecture Search 여기서 우리는 우리의 방법을 CIFAR10에 대한 간단 NAS 실험에 적용한다. NAS는 여러 아키텍쳐에 대해, 전체 데이터셋에 대해 여러번 학습하고 validation set에 대해서 최고의 성능을 보이는 모델을 고르는 것이기에 일반적으로 많은 비용을 요구한다. 우리의 목표는, 우리의 응축된 이미지가 최고의 네트워크를 찾아내기 위해 다수의 네트워크를 학습하는 과정을 효율적으로 만들어 주는것을 확인하는 것이다. 이를 위해 우리는 uniform grid에 대해 하이퍼파라미터 $W, N, A, P, D$를 변경하여 720개의 ConvNet 탐색 공간을 구성하였다. 그리고 Random sampling, Herding, DC의 방법으로 얻어진 세 개의 작은 데이터셋(10 이미지/클래스) 100 epoch으로 훈련했다. 응축된 이미지를 훈련할 때 default ConvNet 아키텍쳐만 사용해서 한 번만 응축했고, 그것을 모든 종류의 아키텍쳐에 사용했다. 또한 우리는 전체 트레이닝 셋에 대해서 학습되지만, 트레이닝 반복 횟수는 small proxy dataset의 반복 만큼만 훈련하는, 즉 동일한 양의 계산만 진행하는 early-stopping 방법과도 비교했다.

표4에서 5개의 모델 중 최고의 평균 테스트 성능은 전체 데이터에 대해서 훈련한 모델이 차지했다. validation 정확도 사이의 Spearman's rank correlation coefficient도 적혀있는데 이는 프록시 데이터셋과 전체 데이터셋에 대해서 선택된 10개의 모델들을 훈련함으로써 얻을 수 있다. 표에는 720개의 아키텍쳐를 NVIDIA-GTX1080-TI GPU에서 훈련시키는데 걸리는 시간이 적혀있다. 그리고 트레이닝 이미지의 메모리 사용량이 적혀있다. 우리의 방법은 최고의 테스트 성능과(84.5%), performance correlation(0.79)를 달성했다. 그러면서 탐색 시간을 상당히 줄였고(8604.3분에서 18.8분으로) 메모리 사용 공간 또한 줄였다(50000개의 이미지에서 100개의 이미지로). early-stopping 방법이 성능에서는 우리의 모델과 동등한 결과를 냈지만, Correlation(0.42)이 우리보다 적었다. 이는 early-stopping과 전체 데이터셋 훈련 간의 신뢰할 수 없는 성능 상관 관계를 나타낸다. 게다가 early-stopping은 우리가 필요로 하는 이미지보다 100배는 더 많은 훈련 이미지가 필요하다. 합성 이미지셋을 훈련하는데 50분 정도가 한 번 필요하지만(K = 500일때) 수천 혹은 수백만의 candidate architecture를 가진 NAS를 훈련할 때는 이 시간은 무시할 수 있는 시간이다.

4. Conclusion

이 논문에서 우리는 informative한 images로 구성된 작은 데이터 셋을 합성하는 Dataset Condensation 방법을 제안한다. 우리는 이 이미지들이 동일한 수의 오리지널 데이터보다 상당히 data-efficient 하다는 것과, 한 번 생성된 데이터 셋은 architecture 의존적이지 않아서 다른 심층 네트워크에 훈련될 수 있다는 점을 보였다. 한번 훈련되면, 훈련된 데이터셋은 더 작은 메모리 프린트를 가진 곳에서 사용되거나, continual learning, NAS등의 여러 네트워크에서 효율적으로 훈련될 수 있다. 이미지넷과 같이 더 다양성을 가지고 도전적인 데이터셋에 대한 연구들이 앞으로 진행되어야 할 것이다.

---

내용출처 : https://arxiv.org/pdf/2006.05929.pdf

틀린 내용이 있거나 수정할 사항이 있으면 댓글로 알려주시면 감사하겠습니다.