TabR : Tabular Deep Learning Meets Nearest Neighbors in 2023 리뷰

오늘은 Tabular 데이터(정형 데이터)를 다루는 딥러닝 기반의 논문을 리뷰해 보려고 합니다. 기존에는 tabular 데이터를 다룰 때 대부분 Gradient-Boosted Decision Trees (GBDT) 방법을 사용했지만, 최근 tabular 데이터를 위한 딥러닝 기술의 발전으로 DL(Deep Learning) 기반의 방법이 GBDT 방법과 유사하거나 더 좋은 성능을 보여주고 있습니다. 해당 논문에서는 새롭게 제안하는 TabR(Tabular Retrieval) 방법을 통해 여러 Tabular dataset 벤치마크에서 SOTA의 성능을 보여 줍니다.

1. Introduction

Tabular 데이터는 여러 카테고리의 데이터가 표의 형태로 정리되어 있는 것이 일반적입니다. Tabular 데이터는 다양한 분야의 데이터를 정리하는데 용이한 구조이지만, 데이터가 규칙적이지 않고 각 feature의 특성이 달라서 일반적으로 DL 방법 대신 GBDT 방법을 사용했습니다.

하지만 최근 DL 기반 방법이 주목받고 있는데, 이는 검색-증강(retrieval-augmented) 모델을 활용하여 보다 더 좋은 예측을 할 수 있게 되었기 때문입니다. 여기서 검색 기반(retrieval-based) 방식이란 자연어 처리에서 주로 사용되는 방법인데, 특정 질문에 대한 답변(candidates)을 여러가지 뽑은 뒤에 그 중에서 가장 답변에 가까운 것을 뽑아 답변으로 채택하는 방식을 말합니다. 이를 Tabular 데이터셋에 적용한다면, target과 유사한 여러 샘플을 뽑아서 그 중에서 prediction을 하는 형식이라고 이해를 하시면 됩니다.

검색 기반 방법을 사용하면 예측 성능을 향상시킬 수 있는 장점도 있지만, 부가적으로 purely parametric 방법(retrieval-free)에 비해 incremental learning이나 robustness에서의 성능 향상도 얻을 수 있다는 장점이 있습니다.

추가로 GBDT 방법 대신에 DL 방법을 사용하면 domain adaptation, semi-supervised learning 등의 강력한 DL 방법을 적용하여 사용할 수 있는 장점이 있습니다.

해당 논문에서 제시하는 3가지 주요 Contribution은 다음과 같습니다.

1. TabR 방법을 제안하고 새로운 SOTA 성능을 여러 데이터셋에서 달성했습니다.
2. GBDT 모델의 우수성을 설명하기 위해 사용되었던 중간 규모의 벤치마크에서 TabR이 GBDT를 능가했습니다.
3. 기존의 retrieval 기반 모델에서 사용되던 Attention mechanism을 수정하여 더 좋은 모델을 제안합니다.

2. Related Work

Parametric deep learning models

Parametric tabular 딥러닝 모델은 딥러닝의 장점을 실제 tabular 데이터에 응용하고자 하는 연구입니다. 최근 연구에서는 MLP와 유사한 backbone을 사용한 딥러닝 기반의 방법과, Transformer와 유사한 backbone을 가진 딥러닝 기반의 방법이 좋은 성능을 보여주었습니다. 또한 continuous features에 대해서 임베딩 하는 새로운 방법 등을 적용함으로써 GBDT와 tabular DL 방법의 간극을 크게 줄이는데 성공했습니다.

Retrieval-augmented models in general

일반적으로 검색 기반 방법은 다음과 같은 순서로 진행됩니다. 첫 째로, 데이터셋에서 input object와 관련성이 있는 샘플들을 검색합니다. 그런 다음 input object와 뽑힌 샘플(input과 관련있는)들을 함께 가공하여 input object에 대한 더 좋은 최종 예측을 가능하게 합니다. 가장 흔하게 사용되는 검색 기반 방식은 local learning paradigm이 있고, 가장 쉽게 적용할 수 있는 모델 중 하나는 $k$-nearest neighbors (kNN) 알고리즘이 있습니다.

Retrieval-augmented models for tabular data problems

기존에 존재하는 검색-증강 기반 DL모델들은 성능이 simple-parametric 방법에 비해 조금 좋은 정도에 그쳤습니다. 그리고 무거운 Transformer 같은 구조를 사용하면서 계산량이 증가하게 되었습니다. 해당 논문에서 제시하는 방법은 이전의 연구들에 비해 단 한개의 single-head attention 모듈을 사용하고, 해당 모듈을 cutomize 하여 기존의 방법들을 뛰어넘는 성능을 보여줍니다.

3. TabR

Preliminaries

내용 설명에 앞서 사용되는 텀을 먼저 정리하고자 합니다. 데이터셋은 $\{(x_i, y_i)\}^n_{i=1}$ 이고 $x_i \in \mathbb{X}$ 는 객체의 $i$ 번째 feature를, $y_i \in \mathbb{Y}$는 객체의 $i$번째 label을 각각 나타냅니다. 본 논문에서는 binary classification $\mathbb{Y} = \{0, 1\}$, multiclass classification $\mathbb{Y} = \{0, \cdots, C\}$, 그리고 regression $\mathbb{Y} = \mathbb{R}$의 3가지 Task에 대해서 고려했습니다. 데이터셋은 $\overline{1, n} = I_{train} \cup I_{val} \cup I_{test}$ 의 세 영역으로 나누었으며, validation 파트는 early stopping 과 하이퍼 파라미터 튜닝에 사용되었습니다.

검색 기반의 방법을 사용할 때 사용되는 "candidates"는 $I_{cand} \subseteq I_{train}$ 즉, 훈련 데이터셋으로 부터 얻습니다.

실험 시에는 적절한 앙상블 성능을 얻기 위해서 15개의 random seed를 사용해 겹치지 않는 3개의 그룹으로 나누어 각 그룹의 평균 성능을 계산하고, 3개의 그룹의 평균 성능으로 결과를 표시 하였습니다.

Architecture

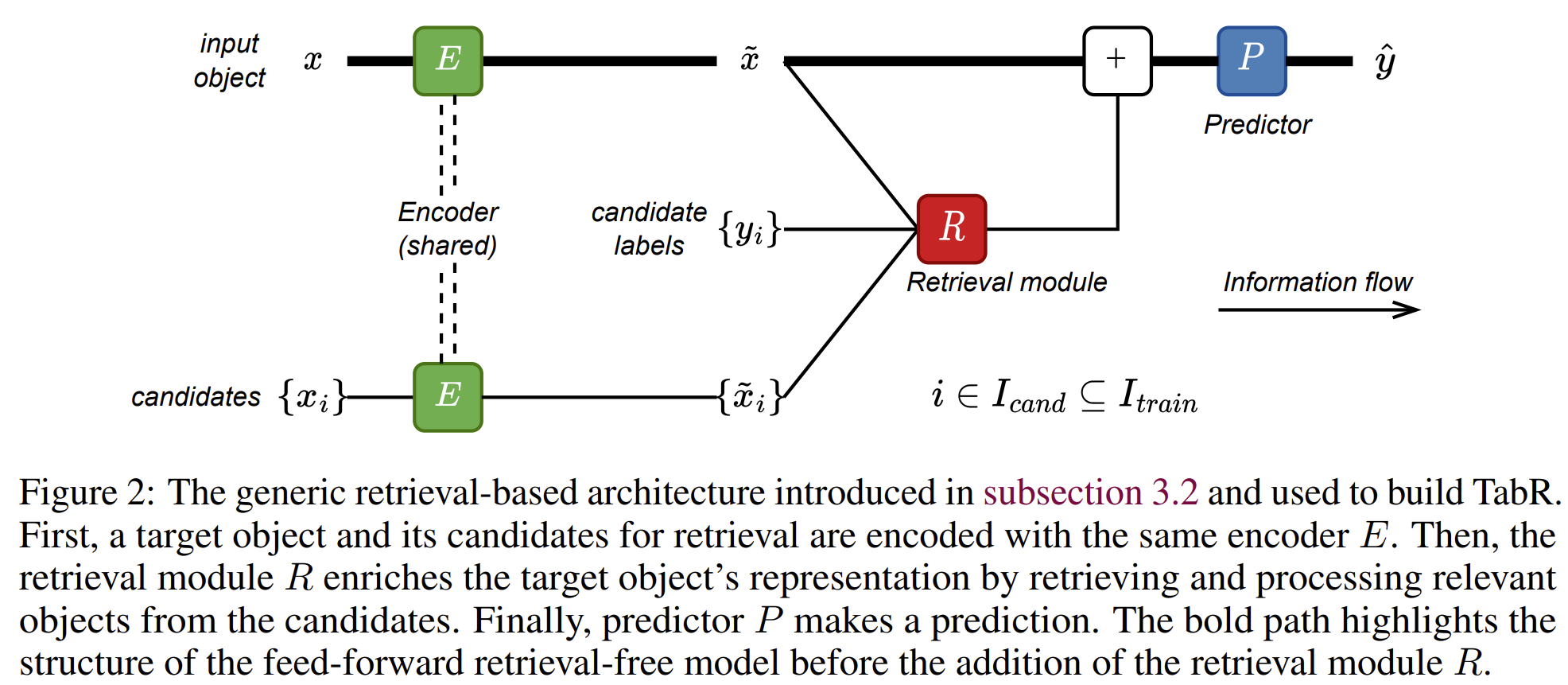
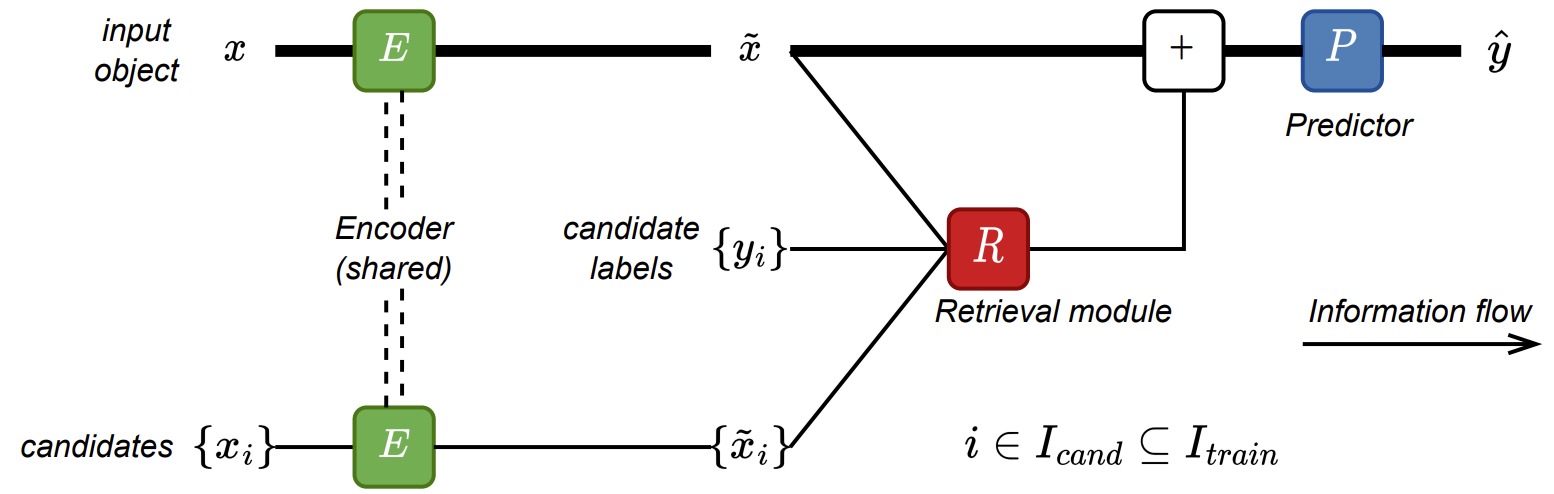
본 논문은 기존에 사용되던 기본 구조로부터 하나씩 개선해 나가며 점진적으로 확장하는 방식으로 제안하는 TabR 방법을 설명합니다. 일반적인 feed-forward retrieval-free network $f(x) = P(E(x))$ 는 각각 encoder $E : \mathbb{X} \rightarrow \mathbb{R}^d$ 와 predictor $P : \mathbb{R}^d \rightarrow \hat{\mathbb{Y}}$ 으로 이루어집니다. 본 논문에서 제안하는 방식은 이곳에 retrieval module $R$을 residual branch로 더해주어 구현됩니다. 위의 그림에서 $\tilde{x} \in \mathbb{R}^d$ 는 타겟 object의 중간 표현이고, $\{\tilde{x}_i\}_{i \in I_{cand}} \subset \mathbb{R}^d$ 는 candidates의 중간 표현이고, $\{y_i\}_{i \in I_{cand}} \subset \mathbb{Y}$ 는 candidates의 label 입니다.

Encoder 와 Predictor는 각각 위의 그림과 같은 구조를 가집니다. 본 논문에서는 encoder, predictor에 대해서는 크게 수정하지 않고 위의 구조를 그대로 사용합니다. Encoder의 앞에 있는 $Input \ Module$ 은 feature normalization이나 one-hot encoding 같은 input processing을 담당합니다.

Retrieval module

본 논문에서는 $k$-nearest neighbor 방법을 응용한 retrieval module을 제안합니다. 위에 있는 그림의 간결성을 위해서 생략한 내용은 다음과 같습니다.

1. 만약 encoder $E$가 최소한 하나의 블록을 소유하고 있다면$(N_E > 0)$ retrieval module $R$ 을 지나기 전에 $\hat{x}$과 모든 $\hat{x_i}$는 shared layer normalization으로 일반화 됩니다.
2. 선택적으로, target object는 유사도 점수 $\mathcal{S}(\tilde{x}, \tilde{x})$를 사용하여 $(m+1)$-th context 객체에 무조건적(top-m 작업을 무시할 때)으로 더해질 수 있습니다.
3. softmax 함수에 의해 생성된 가중치에는 Dropout이 적용됩니다.
4. 논문 전반에 걸쳐 $m = 96$ 그리고 $I_{cand} = I_{train}$이 사용됩니다.

Step-0. The vanilla-attention-like baseline

self-attention 동작은 이전의 연구에서 target 객체와 candidate/context 객체 사이의 상호관계를 파악하기 위해 종종 사용되었습니다. $W_Q, W_K, W_V$가 각각 linear layer일때, 베이스라인은 다음과 같습니다.

Step-0의 성능은 MLP와 유사한 딥러닝 구조를 사용했을 경우와 비슷한 성능을 보여줍니다.

Step-1. Adding context labels

Step-0 에서 성능을 향상시키기 위한 자연스러운 접근법은 context 객체의 label 정보를 추가해 주는 것입니다. 위의 식에서 Value module에 context label 정보를 추가해 줍니다. 그러나 이 방법 만으로는 눈에 뛸만한 성능 향상을 얻지는 못했습니다.

Step-2. Improving the similarity module

경험적으로 $W_Q$를 사용하는 내적 방법 대신에 $L_2$ 거리를 사용하여 유사도를 구하는 것이 상당한 성능 향상을 이루는 것을 본 논문의 저자는 발견했습니다. 따라서 similarity module의 내적을 $L_2$ 거리 방법으로 대체합니다.

Step-3. Improving the value module $\mathcal{V}$

Value module의 개선을 위해 최근에 제안된 DNNR 방법의 kNN 알고리즘을 사용합니다. 즉 target 객체의 표현을 가져와서 value module의 표현력을 더 증가 시키는 것이 목적입니다. 직관적으로 $W_Y(y_i)$는 context 객체의 "raw" 한 기여라고 본다면, $T(W_K(\tilde{x}) - W_K(\tilde{x_i}))$ 텀은 "correction" 으로 볼 수 있습니다. 여기서 $T$는 key space 임베딩 공간 상에서의 차이를 해석해 줍니다.

Step-4. TabR

마지막으로, 경험에 의해서 유사도 모듈의 scaling term $d^{-1/2}$를 제거하는 것과 target 객체를 context에 포함하지 않는 것이 더 좋은 평균 성능을 보인다는 결과를 얻었습니다. 따라서 본 논문에서 제안하는 TabR 방법은 다음과 같이 정리됩니다.

4. Experiments Results

Retrieval module의 개선점들을 각 단계마다 적용한 성능을 위의 표2에서 확인할 수 있습니다. 각 데이터셋 별로 이전 단계보다 좋은 성능을 보이는 단계에 밑줄이 그어져 있습니다.

본 논문에서 제안한 TabR 방법은 여러 tabular benchmark dataset에서 좋은 성능을 보여줍니다. 위의 표3는 기존에 사용되었던 DL 기반의 방법들과 성능을 비교 해서 보여줍니다. 오른쪽에 있는 평균 rank 수치를 보았을 때, 새롭게 제안된 TabR, TabR-S(Simple) 모델이 1.0 대의 평균 rank를 보이며 좋은 성능을 보여줍니다.

DL 기반의 방법들 뿐만 아니라 Tabular dataset에서 주로 사용되었던 GBDT 방법들과의 성능 비교표를 위 표4에서 확인할 수 있습니다. 마찬가지로 TabR 방법이 GBDT 방법들보다 더 좋은 성능을 보여줍니다.

5. Conclusion

본 논문에서는 기존에 사용되던 검색 기반의 DL 방법을 가져와 Retrieval module 내의 similarity module과 value module을 개선하여 최적의 성능을 달성하였습니다. 뿐만 아니라 Retrieval Candidate에 따른 최종 예측 성능 분석과 같은 새로운 분석의 기회도 열어 주었습니다. 추후에는 검색 기반 방식의 효율성을 높이고, 수 백만개의 데이터도 처리할 수 있는 모델을 만드는 것을 future works로 제시합니다.

논문 출처 : https://arxiv.org/abs/2307.14338

Yury Gorishniy, Ivan Rubachev, Nikolay Kartashev, Daniil Shlenskii, Akim Kotelnikov, Artem Babenko. TabR : Tabular Deep Learning Meets Nearest Neighbors In 2023. ICLR 2024.