1. Linear Regression이란?
x값을 넣었을 때, y 값을 예측하는 모델을 만들기 위해서, 예측하는 여러 가지 선을 그릴 수 있다. 이 중에서 각 점이 예측선에 가깝게 일치할 때, 예측을 잘한다고 할 수 있다. 데이터를 정확하게 예측하는 식을 찾는 과정을 Linear Regression이라고 한다.
Linear Regression은 RSS(Residual Sum of Squares)값을 최소로 만드는 w를 찾는 과정이다.
- RSS = (실제값-예측값)의 제곱의 합
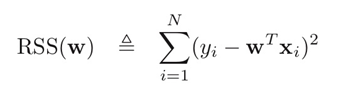
2. 회귀 종류와 손실
2-1. Quantile Regression(분위수 회귀)
- 회귀 분석은 결과 변수의 평균을 예측한다.
- Quantile Regression은 결과 변수의 q-분위수를 예측한다.
- 확률변수 Y가 있고, 0.7 분위수일 때, Y의 분포를 0.7대 0.3으로 가르는 수라고 생각할 수 있다.
Quantile Loss(분위수 손실)
Quantile Loss는 q-분위수를 찾기 위한 손실 함수라고 할 수 있다. q-분위수 추정값에 따라 q 또는 q-1로 달라지는 weighted MAE.
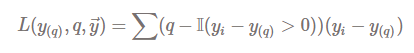
2-2. Huber Regression
Linear Regression은 RSS(Residual Sum of Squares)를 최소화하는 w를 찾는 것이 목적이다.
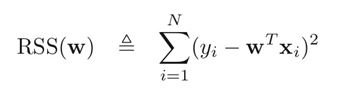
RSS는 에러를 제곱하여 더하는 형태이기 때문에, 이상치가 많다면 모델 왜곡이 크게 된다. 따라서 선형 회귀 모델들이 이상치에 민감하다는 단점을 가진다. 이 단점을 극복하기 위해 이상치에 민감하지 않은 Linear Regression을 Robust Linear Regression이라고 한다.
Robust Linear Regression의 예로는 Laplace Regression과 Huber Regression이 있다.
Huber Loss
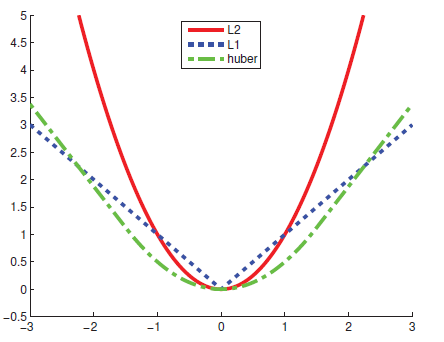
Hubr loss function은 밑의 수식에서처럼 함수 값을 최소화하는 w를 찾는다. 에러(r)의 절대값<델타 이면 L2 에러를 취하고, r의 절대값>델타이면 L1을 취한다.
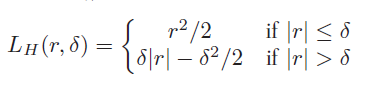
- r > 델타 : 에러가 클 때, L1을 취한다.
- L1은 파란선 그래프
- 이상치에 민감한 L2의 단점을 극복
- r <= 델타 : 에러가 작을 때, L2를 취한다.
- L2는 빨간선 U자형 그래프
- 미분이 불가능한 L1의 단점을 극복
2-3. Absolute loss, Squared loss
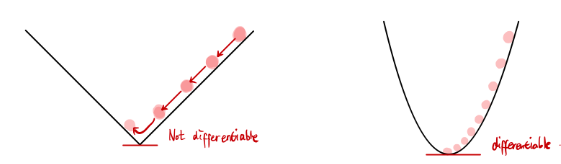
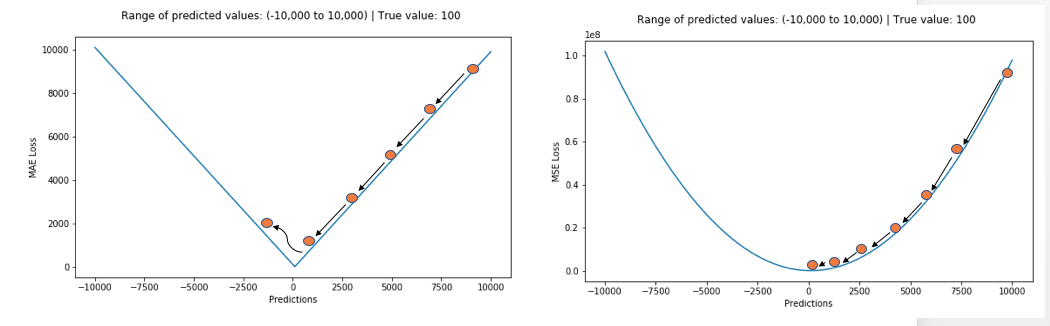
MAE Loss(L1 Loss), absolute loss VS MSE Loss(L2 Loss), squared loss
MAE와 연관해서 설명이 많이 된다. squared loss를 더 많이 사용하는 이유는 absolute loss는 왼쪽 그림처럼 기울기의 차이가 없기 때문이다. 기울기가 +, - 방향에 따라 같은 기울기가 나오기 때문에, 방향은 알 수 있지만 같은 미분값이 나와서 기울기가 큰지 작은지 비교할 수 없다.
결론
절대값 개념 바탕 Quantile Regression, absolute loss
에러 제곱 개념의 바탕 Huber Loss, squared loss
-> 이상치에 강한(Robust)한 모델, Quantile, Huber
-> 손실함수까지 공부해야지 제대로 이해가 될 것 같다.
참고
선형회귀 : https://process-mining.tistory.com/125
Robust Linear Regression : https://process-mining.tistory.com/130
분위수 손실 : http://ds.sumeun.org/?p=2173
분위수 손실2 : https://blog.naver.com/seolhee1213/222829541778
분위수 재난지원금 예시 : https://blog.naver.com/mmysmmys/222520829539
squared loss, absolute loss : https://bo-10000.tistory.com/44
