분류 모델의 평가 지표(Confusion Matrix, Accuracy, Precision, Recall, Trade-off, 임계값 Threshold, ROC-Curve, AUC)

hyemin·2022년 11월 24일

ML

목록 보기

9/9

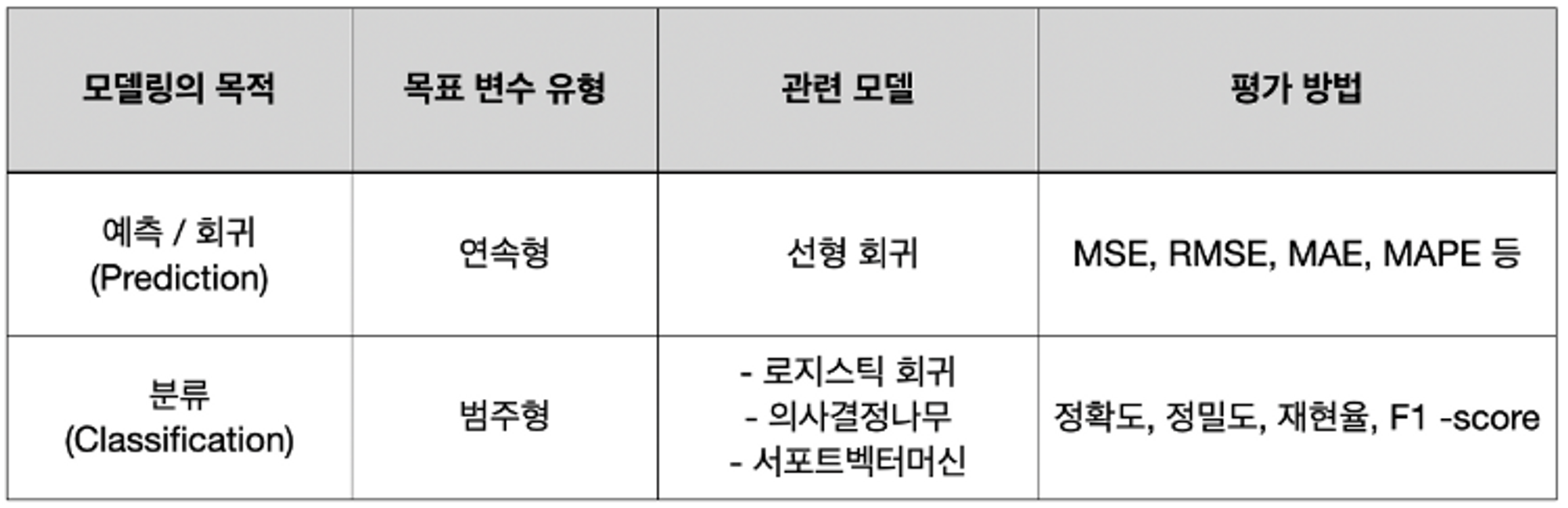
성능 평가 지표(Evaluation Metrics)

Metric : a set of numbers that give information about a particular process or activity. 어떤 성능 또는 활동에 대한 정보를 나타내는 숫자

머신러닝에서는 학습이 잘 되었는지 확인하기 위한 Metircs가 존재한다. 성능 평가란, 실제값과 모델에 의해 예측된 값을 비교하여 두 값의 차이(오차)를 구하는 것이다. (실제값-예측값)=0이면 오차가 없는 것이며, 현실적으로 오차가 없기는 힘들기 때문에 어느 정도까지 오차를 허용할 지 결정한다.

출처: https://bigdaheta.tistory.com/53

분류모델의 평가 지표

오차 행렬(ConfusionMatrix)

학습된 분류 모델이 예측을 수행하면서 얼마나 헷갈리고(confused) 있는지 보여주는 지표이다. 분류의 나머지 평가방법에 포함되는 TN, FP, FN, TP라는 용어를 오차행렬을 통해 익힐 수 있다.

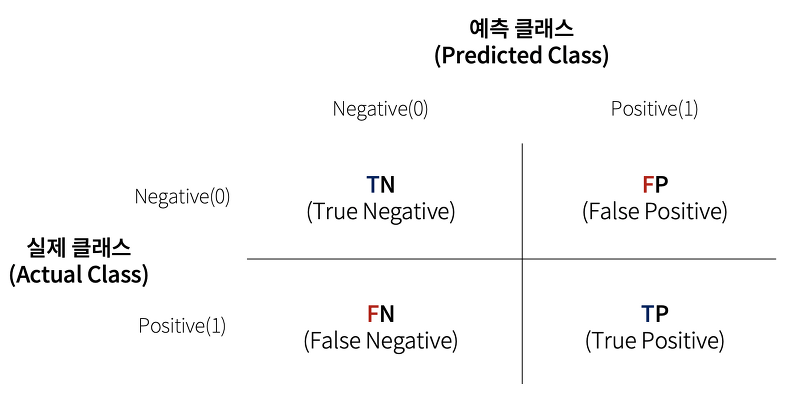
출처 : https://velog.io/@sset2323/03-02.-%EC%98%A4%EC%B0%A8-%ED%96%89%EB%A0%AC-Confusion-Matrix

TP(True Positive) : 예측값을 Positive(1)로 예측, 실제값도 Positive(1)
TN(True Negative) : 예측값을 Negative(0)로 예측, 실제값도 Negative(0)
FP(False Positive) : 예측값을 Positive(1)로 예측, 실제값은 Negative(0) - 1종 오류
FN(False Negative) : 예측값을 Negave(0)로 예측, 실제값은 Positive(1) - 2종 오류
1종 오류와 2종 오류의 경중
- 중고차 성능 판별(Precision)
  - 좋은 자동차라고 예측(Positive), 실제로는 좋지 않은 자동차(False) : FP, 1종 오류, 치명적(좋지 않은 자동차를 예측을 믿고 구매 시)
  - 좋지 않은 자동차라고 예측(Negative), 실제로는 좋은 자동차(False) : FN, 2종 오류, 좋은 자동차를 나쁜 자동차로 예측해서 구매 하지 않더라도 큰 피해 없음
- 스팸메일(Precision)
  - 스팸으로 예측(Positive), 실제로는 스팸이 아님(False) : FP, 1종 오류, 치명적(받아야 할 업무 메일이 스팸 메일로 분류되서 못받을 수 있음)
  - 스팸이 아니라고 예측(Negative), 실제로는 스팸(False) : FN, 2종 오류, 귀찮지만 스팸 확인 후 삭제하면 되니까 큰 피해 없음
- 암환자 진단(Recall)
  - 암이라고 예측(Positive), 실제로는 암이 아님(False) : FP, 1종 오류, 화는 나지만 큰 피해 없음
  - 암이 아니라고 예측(Negative), 실제로는 암환자(False) : FN, 2종 오류, 치명적(암 환자를 건강하다고 판별하여 치료를 놓치게 할 수 있음)
    2종 오류가 더 치명적. 암 환자를 건강하다고 판별하는 경우가 더 위험하다.

(참고) 예측값을 Predicted, 실제값을 Actual이라고 표현하기도 한다.

Accuracy(정확도, 정분류율)

$Accuracy = \frac{TP+TN}{TP + TN + FN + FP}$

전체 데이터(Total=TP+TN+FN+FP) 중에서 모델이 모두 정확 하게 맞춘(TP+TN) 비율

단점 : 불균형한 데이터(imbalanced data)의 경우에는 정확도는 적합한 지표가 아니다.

예를 들어 대게 사진 10000장을 가지고 있고, 킹크랩 사진을 10장 가지고 있을 때, 모델은 단순히 모든 사진이 대게라고 분류할 수 있다. 그렇다면 보기에는 99.9%의 정확도지만, 분류는 제대로 안되었다.
다른 예로는 서울에 시간당 1m 이상의 눈이 내릴지를 예측한다고 했을 때, 서울에는 그렇게 눈이 내릴 확률이 드물다. 무조건 Negative를 예측하면 99.9% 정도의 정확도는 나타내지만, True Positive는 하나도 발견하지 못하기 때문에 분류를 제대로 못했다고 할 수 있다.

(참고) 오분류율(Error Rate)

전체 데이터(Total=TP+TN+FN+FP) 중에서 모델이 틀린(FN+FP) 비율

$Error Rate = \frac{FN+FP}{TP + TN + FN + FP}$

Precision(정밀도)

예측값(Positive) 중에서 실제값이 Positive인 비율 == 예측값이 얼마나 정확한가 == 정답이 아닌데 정답이라고 예측한 것이 있는가

$Precision = \frac{TP}{TP + FP}$
$Precision = \frac{detected\ TRUE}{whole \ detections\ an algotithm}$

양성(Positive) 예측 성능을 더욱 정밀하게 측정하기 위한 지표로, TP를 높이고, FP를 낮추는 것에 초점을 맞춘다.
스팸메일과 같이 Negative 데이터를 Positive로 잘못(False)예측하면 큰 피해가 발생하는 경우

Recall(재현율)

실제값 중에서 모델이 검출한 실제값의 비율 == 정답(참)인데도 정답을 못찾는 것이 있는가
$Recall = \frac{TP}{FN + TP}$

잘못된 Negative를 줄이기 위한 지표로, FN을 낮추는 것에 초점을 맞춘다.
- 재현율을 높이기 위한 첫 번째 방법 : TP값 증가
- 재현율을 높이기 위한 두 번째 방법 : FN 값 감소
암환자 예측과 같이 Positive 데이터를 Negative로 잘못(False) 예측하면 큰 피해가 발생하는 경우

Precision / Recall Trade-off

Trade-off : Precision, Recall은 상호보완적인 평가 지표이므로 한쪽을 높이면, 다른 한 쪽은 줄어든다.

임계값(Threshold)

predict(X_val) 코드를 사용했을 때, X validation에 대한 y의 validation이 0, 1로 분류하는 기준을 임계값이라고 한다.
- 임계값의 기본값은 0.5
- 임계값이 낮아질수록 Positive로 예측할 확률이 높아진다 == 재현율이 증가한다.

출처 : https://sonny-daily-story.tistory.com/18

적절한 임계값을 찾아서 정밀도와 재현율을 효율적으로 만들어야 한다.
아래 그래프에서, 오차 행렬을 그래프로 구현했을 때, 초록색 선이 합격, 불합격을 판단하는 ‘판정 임계점(Decision threshold)’. 오른쪽 그래프는 합격, 불합격을 구별하는 오차가 작기 때문에 더 좋은 ROC 그래프가 그려진다.

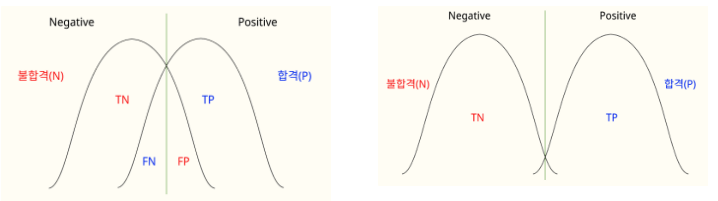
출처 :https://blog.naver.com/wantedlab/222719920948

Threshold 변화에 따른 정밀도와 재현율 시각화(아래)

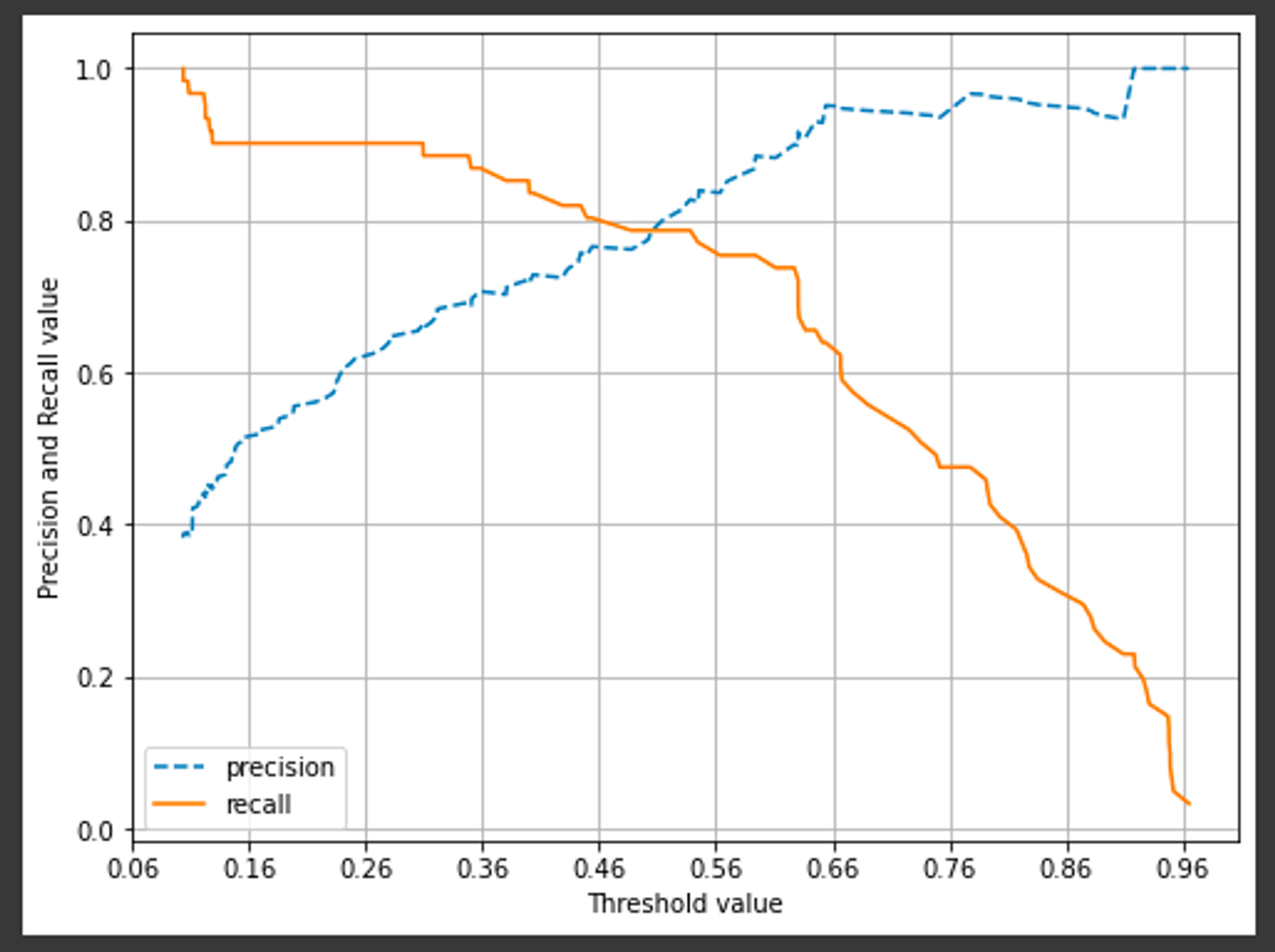
출처 : https://jays-lab.tistory.com/31

ROC-curve, AUC

FPR ==’불합격’ 판단을 내린 경우 중 ‘합격자를 불합격자’라고 잘못 예측한 비율 == Precision과 Recall의 Fall-out
- ROC Curve의 X축
- 0에 가까울수록 좋음 $FPR = \frac{FP}{N} = \frac{FP}{FP+TN} = 1-TNR$
TPR == ‘합격’ 판단을 내린 경우 중 ‘합격자를 합격’이라고 정확하게 예측한 비율
- ROC Curve의 Y축 == 재현율
- 1에 가까울수록 좋음
  $TPR = \frac{TP}{P} = \frac{TP}{TP+FN} = 1-FNR$
ROC-curve와 AUC를 사용하여 분류문제에서 임계값 설정에 대한 모델의 성능을 구할 수 있다.
이진 분류 문제에서는 ROC curve와 AUC 점수를 잘 활용하면 좋은 결과를 낼 수 있다.
ROC 곡선은 FPR과 TPR의 변화 값을 보는데 이용
- 분류 모델의 성능 지표로 사용되는 것은 AUC값
AUC(Area Under Curve)는 ROC 곡선 밑의 면적을 구한 것
- 0과 1 사이의 범위
- 일반적으로 1에 가까울 수록 좋은 것
- 0.5에 가까울수록 학습이 제대로 이루어지지 않은 모델
- 높이려면 FPR이 작은 상태에서 큰 TRP을 얻어야 함 == 가운데 직선에서 멀어지고, 왼쪽 상단 모서리쪽으로 가파르게 올라갈수록 면적이 1에 가까운 좋은 모델

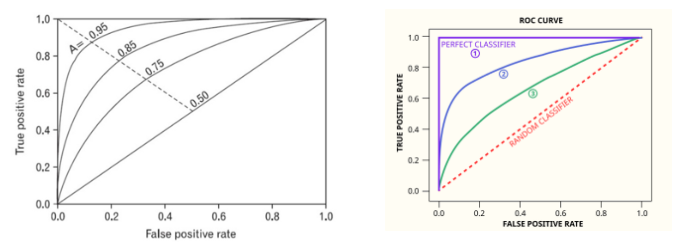
출처 : https://libertegrace.tistory.com/entry/Evaluation1
https://blog.naver.com/wantedlab/222719920948

F1 Score

F1 score = \frac{2}{\frac{1}{recall}+\frac{1}{precision}} = 2 *\frac{precision*recall}{precision+recall}

정밀도와 재현율이 모두 중요할 때, 조화 평균 내어 하나의 수치로 나타낸 지표

F1 Score는 정밀도와 재현율이 어느 한쪽에 치우치지 않는 수치를 나타낼 때, 상대적으로 높은 값을 가진다.
Precision과 Recall중 더 작은 값에 영향을 많이 받게 하기 위함이다.
- precision = 0.9, recall = 0.1 ⇒ f1_score = 0.18
- precision = 0.6, recall = 0.4 ⇒ f1_score = 0.24