[31일차]데이터 정규화와 스케일링 기법

정규화가 필요한 이유

• 데이터에서 하나의 instance(sample)는 그것이 가진 여러 속성값들을 이용해서 표현이 가능하다.
  이 속성값들을 feature라고 한다.
  (e.g. 엑셀 테이블에서 row는 sample, column은 sample들이 가지는 속성값을 의미)
• feature들간의 크기 및 단위가 들쭉날쭉 하거나 가지는 값의 범위가 크게 다른 경우,
  혹은 이상치(outlier)문제가 심각한 경우
  (이상치 : 평균 연봉을 구할 때 회장님의 연봉까지 넣는다면! 회장님의 연봉처럼 팍 튀는 데이터를 이상치라고 함.)
  데이터 분석이 어려워지거나 머신러닝, 딥러닝 방법을 적용하기 어려워지는 경우가 있다.
• 특히, 머신 러닝 모델에 feature 값들을 input으로 사용하는 경우
  feature의 스케일이 들쭉날쭉하다면 모델이 데이터를 이상하게 해석할 우려가 있다.

아래와 같이 각 feature 값들의 크기가 다른 경우, 스케일이 큰 ‘연봉’만을 중요한 feature로 모델이 해석하게 될 수도 있다는 것.

- 이때 정규화와 스케일링을 통해 feature들이 가지는 값의 범위를 일정하게 맞춰주는 과정이 필요하다.

정규화(Normalization)

여러가지 값(feature)들이 가지는 범위의 차이를 왜곡하지 않으면서 범위를 맞추는 것

앞으로 우리는 아래의 정규화 작업을 진행할 것이다.

1. Min-max Normalization
2. Z-score Normalization(Standardization / 표준화)
3. Log scaling

Min-max Normalization

모든 feature값이 [0,1] 사이에 위치하도록 scaling 하는 기법

• 분모는 feature가 가질 수 있는 max값과 min값의 차이를 두고,
  분자는 해당 feature값과 min값의 차이로 둔다.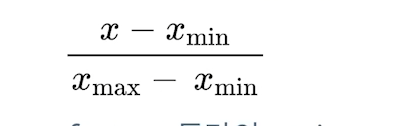

  

• feature들간의 variance 패턴은 그대로 유지한 채로 feature가 scaling 된다.
  • variance 패턴 : 데이터가 분포되어있는 비율
• 다르게 이야기 하면, 특정 feature만 variance가 매우 큰 경우,
  특히 이상치(outlier)가 존재하는 경우
  여전히 feature간의 scaling이 데이터 분석에 적절하지 않을 수 있다.

Z-score Normalization(Standardization / 표준화)

Feature 값들이 μ(평균)=0, 𝝈(표준편차)=1 값을 가지는 정규분포를 따르도록 스케일링하는 기법

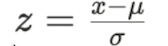
즉, Feature값을 평균값으로 뺀 후 표준편차값으로 나눈 값을 사용한다.

이때 z 값을 표준점수(z-score) 라고 한다.

• Outlier 문제에 상대적으로 robust(문제에 영향을 덜 주는)한 스케일링 방법이다.

• 다만 , Min-max Normalization 처럼 feature값이 가지는 최소-최대값 범위가 정해지지 않는 단점이 있다.

• 대부분의 머신러닝 기법(선형회귀, 로지스틱 회귀, SVM, Neural Networks)들을 활용하는 경우 input에 Standardization을 적용해야 하는 경우가 많다.
  특히, Gradient descent(딥러닝)를 활용한 학습 과정을 안정시켜주고 빠른 수렴을 가능케 한다.

• z-score가 ±1.5𝝈, ±2𝝈를 벗어나는 경우 해당 데이터를 이상치로 간주하고 제거할 수 있다.

Log 스케일링

• Feature 값들이 exponential 한 분포를 가지는 경우(아래와 같이) feature 값들에 log 연산을 취하여 스케일링할 수 있다.
  

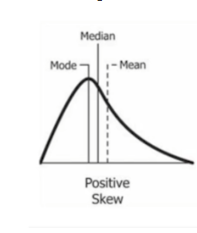
e.g. 대한민국 국민 연봉의 분포

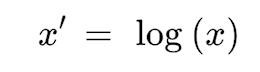
• 비슷하게 square root 연산을 취하거나
  반대의 분포를 가지는 경우 power / exponential 연산을 통해 스케일링 해볼 수 있다.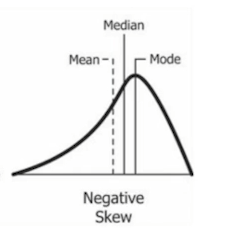

  

• 다양한 스케일링을 통해
  데이터가 좀 더 정규분포에 가까워지도록 스케일링하며
  outlier 문제에도 좀 더 적극적으로 대응이 가능하다.