가설검정

통계적 추정

• 통계적 추정 : 모집단의 모수θ를 표본들의 통계값을 이용해서 추정하는 방법
• 점추정 : 모집단의 특성을 단일한 값으로 추정
  이때 점추정값 θ^은 표본값 X1,…,Xn 들의 함수이다.
• 평향 : 추정량의 기댓값과 모수의 차이 (E(θ^)-θ)
• 평균제곱오차 : E[(θ^-θ)^2]
  • 편차의 제곱에대한 기대값 분산과 비슷한 개념!

기호때문에 난잡해보여서 사진도 추가..!

최대우도 추정량(MLE)

우도함수(Likelihood function) : 확률변수 X1,…,Xn의 결합확률밀도함수 f(X1,…Xn;θ)를 모수 θ에 대한 함수로 볼 때, 이를 우도함수 L(X1,…Xn)라고한다.
즉, 결합확률밀도함수가 모수에 대한 함수일때 우도함수라고 한다.

• 중요성질

  • 확률 변수 X1,…Xn가 서로 독립이고 확률밀도 함수 f(x;θ)에서 얻은 ‘표본이라면

  

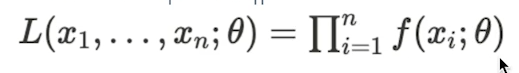
• 최대우도추정(MLE, Maximum likelihood estimate)

  • X1,…Xn을 표본으로 얻을 확률, 즉 우도함수L(X1,…Xn;θ)가 가장 높은 θ^
    즉, MLE는 주어진 관찰값을 가장 잘 설명하는 모수 추정량이다.

정규분포의 MLE 유도

• 정규분포의 우도함수(Likelihood function)는 표본이 나올 확률들을 다 곱한다.
• Log 함수는 단조증가함수이므로 Log likelihood function의 최대값에서의 θ는
  likelihood function의 최대값에서의 θ와 같다.
• Π(Product)에 Log 함수를 취해주면 Σ가 되어 미분을 하기 편해진다.
• 함수를 θ에 대해 편미분()한 값 = 0이 되는 지점에서 얻어지는 θ는 함수의 최대점에서 θ이 가지는 값이다.
  이 때 함수가 Likelihood function인 경우 θ는 MLE가 된다.