확률분포

기댓값

• 기댓값 : 어떤 확률적 사건이 평균적으로 가질 수 있는 값(=평균값,E(x), μ 모집단의 기댓값)

• 이산확률변수의 기댓값: 모든 확률변수에 대해서 값에 xf(x)를 곱하면 기댓값이 나옴.

  

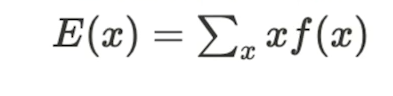
• 연속확률변수의 기댓값: -무한대~무한대의 확률값을 더함. 이때 적분을 진행

  

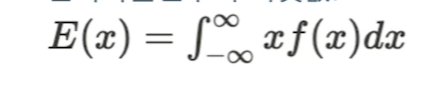
• 기댓값의 성질 5가지
  • E(X+Y) = E(X) + E(Y)
    • 서로다른 확률변수 X,Y의 기대값은 두 기대값의 합과 동일하다.
  • 임의의 실수 a,b,c 에 대해서
    • E(aX+b) = aE(X)+b
    • aX2 + bX + c) = aE(X2) + bE(X) + c
    • E(aX + bY) = aE(X) + bE(Y)
  • 서로 독립인 두 확률변수 X, Y에 대해서
    • E(XY) = E(X)E(Y)

분산

• 분산 : 분포가 평균값으로부터 얼마나 산포되어있는지(Var(X), σ2)
  Var(X) = E[(X-E(X))^2] = E[X^2] - E[X]^2

이산확률변수의 분산:

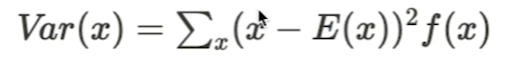
연속확률변수의 분산:

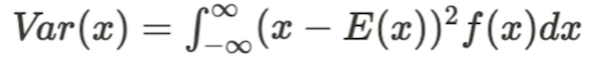
표준편차σ

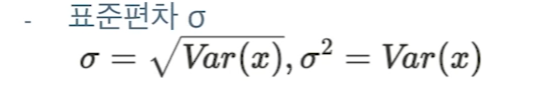
• 분산의 성실:
  • 서로 독립인 두 확률변수 X,Y에 대해서
    • Var(X + Y) = Var(X) + Var(Y)
  • 임의의 실수 a,b,c에 대해
    • Var(aX+b) = a2Var(X)
    • Var(aX+bY) = a2Var(X)+ b2Var(Y)

---

결합확률분포

두 개의 확률변수 X,Y에 대해 P(X=x, Y=y) =f(x,y)를 만족하는 f(x,y)를 확률변수 X,Y의 결합확률분포 혹은 결합확률 {질량/밀도}함수 (joint pmf/pdf) 라고 합니다

예시 1

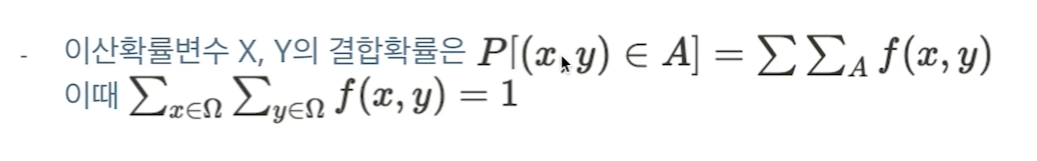
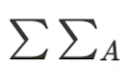
P(x,y)가 A라는 사건에 들어갈 확률 =

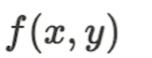
A라고 하는 사건의 집합이

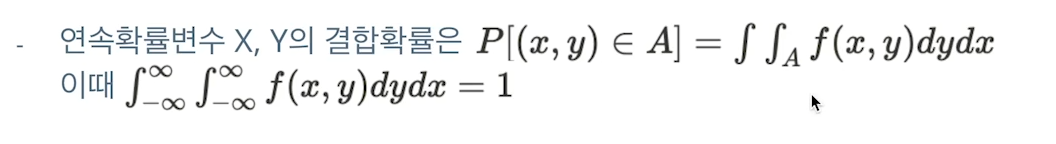
서로다른 x,y의 확률변수를 하나로 보고 확률분포를 구한다.

예시) 주사위를 두번 굴렸을때 1과 3이 나올 확률!

x,y = 1,3 이 된다. 이게 하나의 사건으로 인지됨.

x가 가질수 있는 모든값과 y가 가질수 있는 모든값에 대해서 시그마 해주면 1이 나옴;;;;;;;;;

예시 2

x,y에 대해서 적분을 두번해준 값이 1이 된다…

• (중요) 확률변수 X와 Y가 서로 독립이면 f(x,y) = fX(x)fY(y)