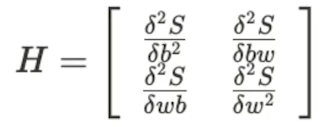선형회귀란?
y=f(x)+ε의 형태로 입력 변수 x와 출력 변수 y 사이의 선형 상관 관계를 모델링하는 분석 기법이다.
e.g. 자동차가 이동한다고 했을 때
시간이 지남에 따라 자동차가 얼마나 움직였는지 알고 싶을 때 선형 회귀를 사용할 수 있다.
자동차가 움직이는 각 시간, 위치를 기록하면 선형회귀라는 도구로 분석하여 ‘시간’과 ‘위치’사이의 규칙을 찾아낼 수 있다.
간단히 말하자면 선형회귀란 시간과 위치 같은 두 개의 것 사이의 관계를 찾아내는 방법이다.
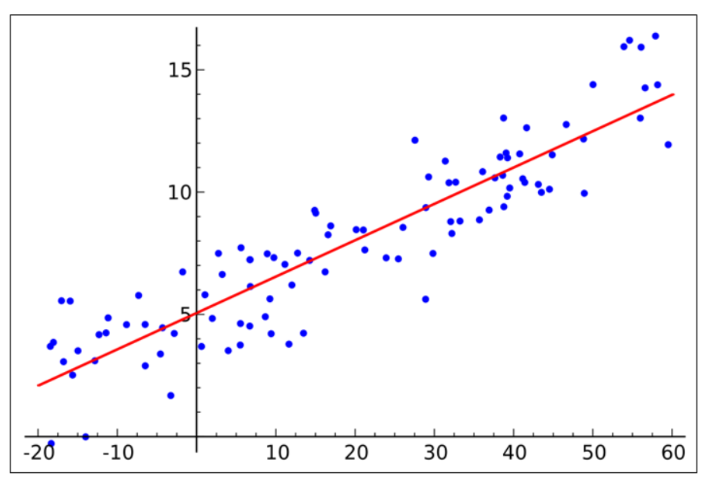
선형회귀를 식으로 표현한다면 아래와 같다고 한다.
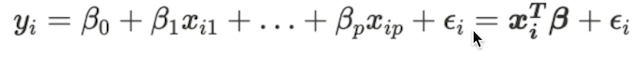
난 봐도 모르겠다.
쉽게 말하면 x는 가로형태의 데이터
| x | 3 | 5 | 21 |
|---|
B는 세로형태의 데이터
| B |
|---|
| 1 |
| 2 |
| 4 |
| 7 |
일때 각 값을 하나씩 곱하고 더한 값+εi = yi가 된다는 것!
- 실무에서는 좀 더 쉽게 부른다.
- x와 y간에 ‘선형의’ 관계에 있다고 하면 아래의식으로 표현한다.
y=b+wx
b = 벡타0을 의미
w = weight라고한다. 선형회귀 식에서 Bp(벡터)를 의미!
- x와 y간에 ‘선형의’ 관계에 있다고 하면 아래의식으로 표현한다.
아래 사진을 보면
-
직선의 기울기를 w
-
직선의 시작위치 (사진은 2)를 b 로본다~
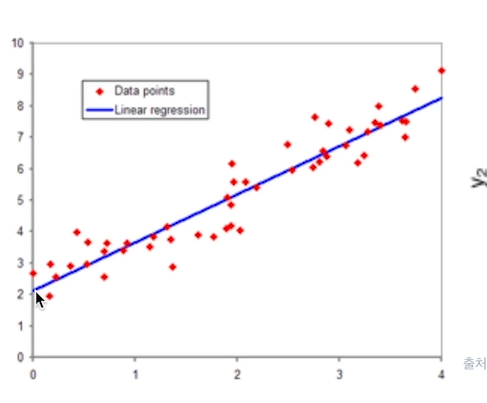
우리의 목표는
b+wx = y 라는 값에 대해서
y와 실제 y가 최대한 가까워지는
w(weight)와 b(bias) 값을 찾는 것 이다.
쉽게 말하면 저기 파란선이 다음에는 어디로 갈지 예측하는 것!
주의!
선형이 아닌 곡선을 그리는 데이터에서는 사용하면 안됨!
선형회귀의 가정
선형회귀에서 오차항 ε에 대한 가정 5가지
- 오차항의 기대치는 0이다.
- 오차항은 일정한 분산을 가진다.
- i ≠j 일때 εi와 εj는 서로 독립이다 / εi = ε 값들을 의미
- 독립변수 X와 εi는 서로 독립이다.
- εi는 정규분포 N(0,σ^2)를 따른다
오차항에 대한 가정을 통해서 다음과 같은 가정이 가능해진다.
- 회귀모형은 선형성을 가진다.
- 종속변수 Y의 분산은 일정한 값 σ^2를 가진다.
- εi와 εj는 서로 독립이며, εi는 자기상관성이 없다.
→시계열 데이터의 경우 자기상관성이 존재할 수 있다.
예를 들어 5초전에 내가 어떤 행동을 했다면 그 행동이 지금하는 행동에 상관성이 없다고 할 수 없기 때문. - Y는 정규분포를 따른다.
선형회귀의 비용함수(Cost function)
비용함수(Cost function)
최근 딥러닝에서 비용함수를 어떻게 잘 설계하느냐가 아주 중요한 내용으로 자리잡고있음.
-
우리의 목적은
실제 Y와 Ypred의 오차를 계산하는 식을 세우고, 이 오차를 최소화 하는 w,b를 찾는 것이다. -
이때, 실제값과 예측값의 오차에 대한 식을
손실함수(loss function), 비용함수, 혹은 목적함수 라고 한다.(다 비슷한 말) -
선형회귀에서는 주로
RSS(Residual sum of squares) 혹은 MSE(Mean squared error)를 비용함수로 사용한다. -
목적을 잘 갖추고 있는지 확인하기 위해서는
우리가 설계한 Cost function이 differentiable(미분가능)하고
플롯이 convex(아래로 볼록)할 때, cost의 최저점.
즉, cost function은 w, b로 각각 편미분 했을 때
0이 되는 지점이다.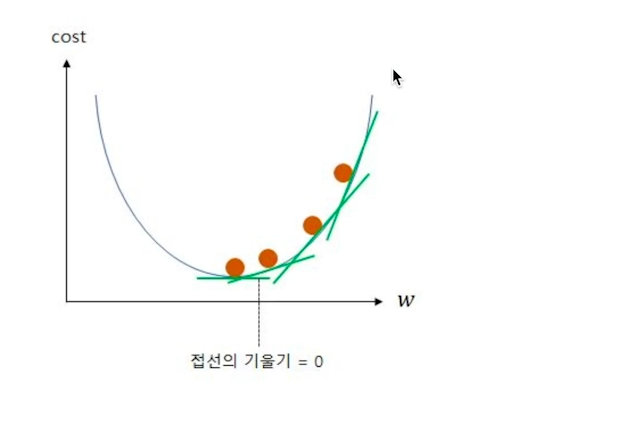
OLS - 최소제곱법
OLS란 오차를 최소화 하는 w, b를 추정하는 방법이다.
-
ε의 제곱의 합이 최소가 되는 점을 찾기 위해서는
ε의 제곱의 합을 w, b로 표현 후 각 각 편미분 했을 때 0이 되면서
2차 편미분 값이 Positive definite이 되도록 해야된다.(볼록 함수 만족)