Gradient descent 경사 하강법
-
변수가 많아지거나 cost function이 복잡해지는 경우, 최소 제곱법을 통해서 한번에 loss가 최소인 parameter를 추정하기 어렵다.
-
이러한 경우, 각 parameter에 대해서 비용함수(cost function)를 편미분한 값(경사(gradient))을
learning rate a만큼 여러번 업데이트 해주는것을
Gradient descent 경사 하강법 이라고 한다.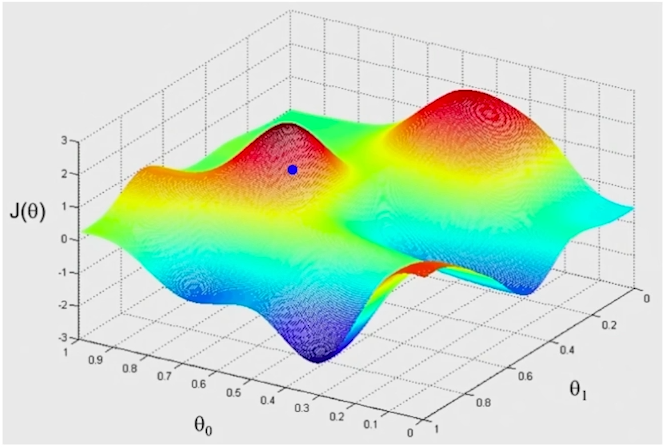
왜 편미분한 값을 경사(gradient)라고 하는가?
아래 그림을 보자
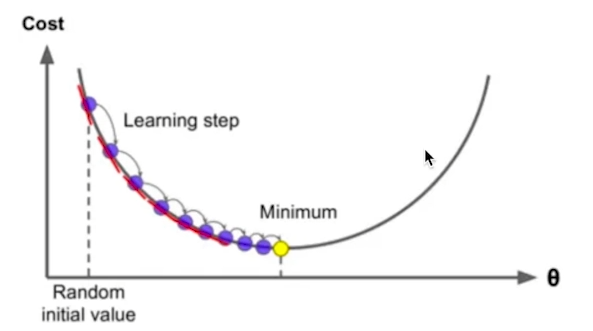
곡선에서 미분이라는 것은 곡선의 기울기를 의미한다.
미분의 반대. 적분은 곡선 밑의 면적을 구하는 연산이다.
즉 parameter(곡선) 에서 cost function을 편미분한 값을 경사(gradient) 라고 한다.
이걸 learning rate라고 함.
이걸 여러번 업데이트 해주면 처음 사진과 같이 나옴.
Gradient descent 경사 하강법 사용 이유
Gradient descent를 사용하는 경우에는 보통 데이터가 매우 많으므로,
[batch Gradient descent] 보다는 [mini-batch stochastic batch Gradient descent(SGD)] 방식으로 학습한다.
단어설명
- batch Gradient descent : 모든 학습 데이터에 대해서 한번에 Gradient descent step을 계산하는방법
- mini-batch stochastic batch Gradient descent(SGD) : 매 스텝에서 mini-batch(여러 뭉태기)만큼의 데이터를 샘플링 해서 학습하는방법
