모델을 제대로 평가하는 metric(지표)를 사용해야 주어진 데이터에서
가장 효과적인 모델을 사용할 수 있다.
모델링 평가방법에 대해서 알아보자
Mean Squared Error(MSE)
오차(틀린값)의 제곱을 평균으로 나눈 값.
즉 평균으로 나눈 값이 0에 가까울 수록 좋은 성능이라고 볼 수 있다.
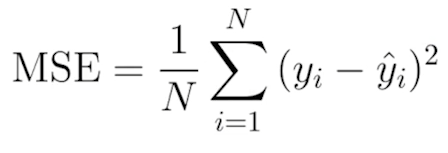
식을 보면 제곱의 합을 사용하기 때문에
오차값이 커질 수 록 데이터 점에 대해서 민감하게 반응한다.(Outlier에 민감하게 반응.)
Mean Absolute Error(MSE)
오차의 절대값을 평균으로 나눈 값
이것 또한 0에 가까울수록 좋은 성능이라고 볼 수 있다.
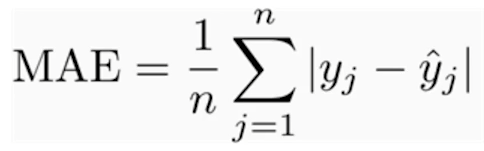
식을 보면 절대값을 사용하기 때문에
오차값이 큰 데이터점에 대해서 상대적으로 덜 민감하게 반응한다.
R-square()
독립변수 x가 종속변수 y를 얼마나 잘 설명하는 지를 나타낸다.
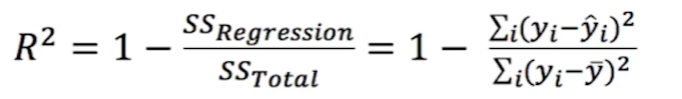
식을보면서 설명해보자
전체 y의 평균으로 부터 각 y값이 멀리 떨어질수록, 예측한 y값과 실제 y값이 가까울수록 1에 가까워진다.
이때 0~1사이 값을 가지며, 1에 가까울수록 좋은 성능이라고 볼 수 있다.
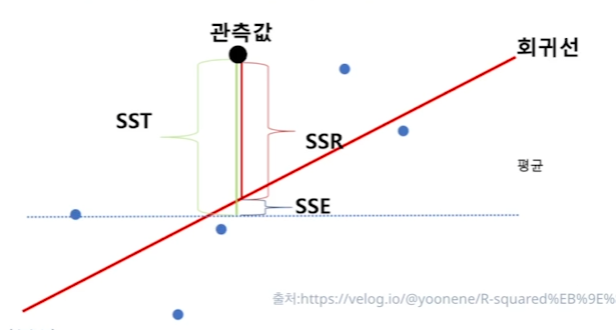
사진에서 데이터 분석법 SST, SSR, SSE이 이렇게 적용되었다고 볼 수 있다.
Classification 평가 방법
분류 평가방법에 대해서 알아보자
이 방법에는 크게 두가지가 있다.
Precision/Recall⭐
면접에서 꼭 물어본다고 한다!!
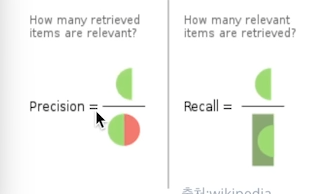
Precision : 실제로 postive인 샘플중 몇개를 positive라고 잡았는지
Recall : positive라고 잡은 샘플 중 몇개가 실제로 positive인지
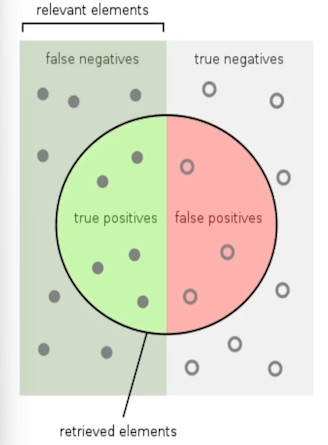
사진과 같은 데이터 셋이 있을때
예측값은 positives, 실제값은 negatives가 된다.
예측값이 맞다면 True, 그럼 이 값은 True negatives로 가게된다.
반대로 예측값이 틀리다면 False, 그럼 이 값은 False negatives로 가게됨.
Precision/recall은 positive threshold(로지스틱 회귀에서 y예측값이 0.5이상으로 되어 있는 것)에 따라 조절이 가능혀며,
False positive가 늘어나는 것이 문제인 경우에는 예측값을 높이는 것이 중요하지만,
false positive가 늘어나도 어떻게든 positive들을 잡아내야 되는경우
(e.g. 전염병, 암 진단)
recall을 높이는 것이 중요하다.(recall을 높이면 원이 커짐)
positive threshold(로지스틱 회귀에서 y예측값이 0.5이상으로 되어 있는 것) 이 0.5보다 더 높일 수 록 원은 더 커질 것이다.
F1 score
Precision과 recall을 둘다 고려한 metric이다.
