4. 분할정복
- 분할: 문제를 동일한 여러 하위 문제로 분할
- 정복: 하위 문제들 재귀적/직접적으로 해결.
- 결합: 하위문제의 해법을 결합해 원본 문제의 해법 겟.
하위 문제가 재귀적으로 풀 수 있을 만큼 클 때 이를 재귀 명제 recursive case라 부름. 재귀적으로 풀 수 없을 만큼 작을 경우가 바탕 명제 base case라 부름(역자: 탈출 조건이라고도 부르는 듯?).
점화
점화 recurrence란 더 작은 입력값에 대한 함수를 의미하는 방정식 혹은 부등식.
- 교체법 substition method: 유계를 추측하여 수학적 귀납법으로 우리의 추측이 맞는지 확인
- 재귀 트리법 recursion-tree method: 점화식을 각 노드가 각 재귀를 의미하는 것으로 치환하여 트리로 표현. 점화식을 해결하기 위해 덧셈에 유계를 주는 방식 사용.
- 마스터 정리 master method: 다음 형식의 점화식의 유계를 제공
- T(n) = aT(n/b) + f(n)
이때 a ≥ 1, b > 1, f(n)는 주어진 함수
- T(n) = aT(n/b) + f(n)
점화 세부 내용
실무에서는 점화식 풀 때 사용한 세부 사항 보통 무시함. 병합 정렬에서 만약 n이 홀수라면 크기가 실제로는 n / 2이 될 수 없음.
근데 이런 유계 조건 사실 보통 무시함. 보통 상수 크기를 갖는 입력의 실행 시간이 상수 시간이라면 이걸 활용한 점화식을 사용한 알고리듬의 실행 시간도 적당히 작은 n에 대해 보통 T(n) = Θ(1)이라고 함. 그래서 그래서 아예 n이 작은 경우를 명시 안하고 퉁치기도 함.
보통 점화식 풀 때 그래서 바닥/천장 함수, 유계조건 등 무시함. 어차피 크게 영향 안 주기 때문. 근데 영향을 줄 땐 알아야 함. 근데 분할정복에 대한 경험과 이론이 말해주길, 딱히 영향 안 줌.
4.1. 최대 부분열 문제
휘발성 화학 회사에 투자한다고 가정. 얘네 주식 상태도 상당히 휘발성임. 한 번에 한 유닛 밖에 못 사고, 나중 날짜에 판매 가능. 해당 날의 거래가 끝나고 나서 구매랑 판매 가능. 대신 주식의 가격이 미래에 어떻게 될지 알려줌. 목적은 이익 극대화.
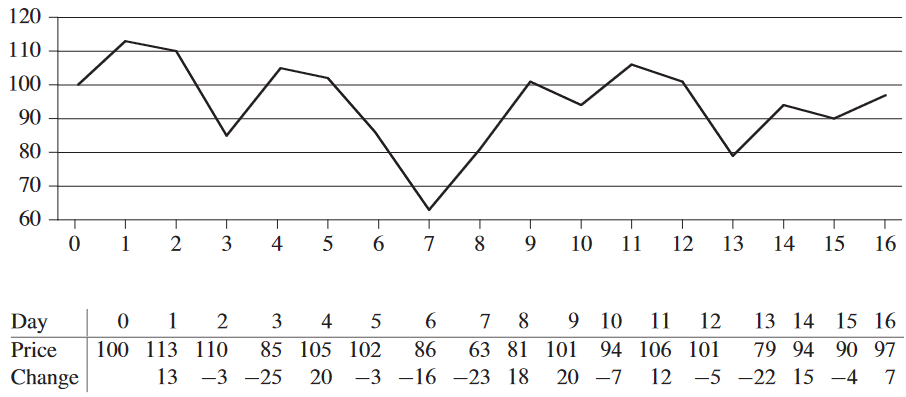
언제나 최소 금액에 구매하고 최대 금액에 판매하는게 제일 많은 이득을 줄 것이라고 아마 바로 가정을 할 것임.
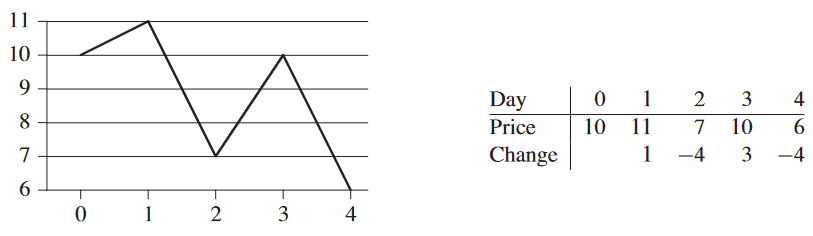
당연히 반례 존재함.
주먹구구식 해법
그냥 모든 조합 시도해보는 거임. 총 n 개의 날이 있으면 날짜 조합은 C(n, 2) 개. C(n, 2)은 Θ(n2)이므로 각 날짜 짝 비교가 상수 시간이 걸릴 것이라고 기도하는 수 밖에 없음. 즉, Ω(n2) 시간 걸림.
변형

실행 시간 o(n2)을 위해 입력을 다른 관점으로 볼 것. 첫날부터 마지막의 전일대비가 최대가 되는 연속된 날을 찾을 것. 매일 가격을 보는 게 아니라, i 번째 날짜가 i - 1 번째 날짜 이후의 값과 i 번째 날짜 이후의 값 간의 차로 보는 것. 위 그림의 아래 행에 해당. 여기서 원소의 합이 최대인 연속된 부분열, 즉 최대 부분열 maximum subarray A를 찾는 것이 정답.

대충 보면 이것도 결국엔 C(n - 1, 2) = Θ(n2) 번의 비교를 해야 함. 연습 문제 4.1-2를 보면 알겠지만 한 부분열의 원소의 총합을 구하는 비용이 부분열의 크기에 비례하겠지만 모든 Θ(n2) 개의 부분열의 각 총합을 구하는 건 기존에 계산한 부분열 값을 통해 구할 수 있어서 주먹구구식 해법은 Θ(n2)이 걸림.
더 효율적인 해법 필요.
최대 부분열이 흥미로운 이유는 음수도 가능해서. 양수만 있었으면 노잼 문제임.
분할정복을 사용한 해법
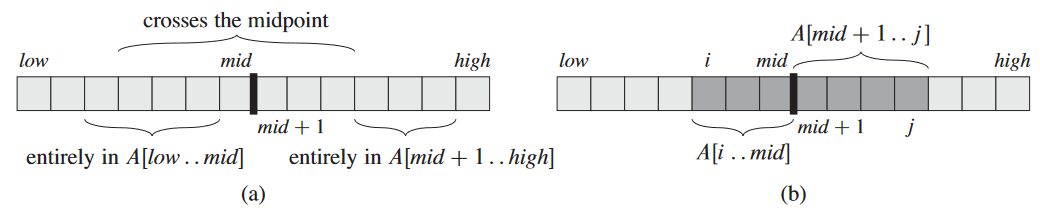
부분열 A[low…high]의 최대 부분열을 찾는다고 가정. 부분열을 최대한 같은 크기로 분할해야 함. 즉, 중간점 mid 구해서 A[low…mid]랑 A[mid + 1…high]가 됨. 이때 A[low…high]의 임의의 연속 부분열 A[i…j]이 다음 중 하나임:
- A[low…mid] 안에 있음, 즉 low ≤ i ≤ j ≤ mid.
- A[mid + 1…high] 안에 있음, 즉 mid < i ≤ j ≤ *high.
- 중간을 거침, 즉 low ≤ i ≤ mid ≤ j ≤ mid.
이때 각 분할된 부분열의 최대 부분열도 재귀적으로 구할 수 있음. 즉, 결국 중간을 지나는 부분열 중에서 최대 총합을 갖는 놈을 따로 구하고, 재귀적으로 구한 나머지 두 분할의 해법, 이렇게 세 가지 후보끼리 비교하면 됨.
중간 지점 지나는 최대 부분열 찾는 건 A[low…high]의 크기에 비례하여 선형 시간안에 찾을 수 있음. A[i…mid]랑 A[mid + 1…j]인 부분열 중 최대값 갖는 놈만 찾으면 됨.
FIND-MAX-CROSSING-SUBARRAY(A, low, mid, high)
left-sum = -∞
sum = 0
for i = mid downto low
sum = sum + A[i]
if sum > left-sum
left-sum = sum
max-left = i
right-sum = -∞
sum = 0
for j = mid + 1 to high
sum = sum + A[j]
if sum > right-sum
right-sum = sum
max-right = j
return (max-left, max-right, left-sum + right-sum)- 줄 1-7: 왼쪽 절반의 최대 부분열 찾음
- 줄 8-14: 위의 절반처럼 오른쪽 절반의 최대 부분열 찾음
FIND-MAX-CROSSING-SUBARRAY(A, low, mid, high)는 Θ(n)만큼 걸림.
이제 분할정복 코드:
FIND-MAXIMUM-SUBARRAY(A, low, high)
1 if high == low
2 return (low, high, A[low]) // 바탕 명제: 원소 하나
3 else mid = ⌊(low + high) / 2⌋
4 (left-low, left-high, left-sum) = FIND-MAXIMUM-SUBARRAY(A, low, mid)
5 (right-low, right-high, right-sum) = FIND-MAXIMUM-SUBARRAY(A, mid + 1, high)
6 (cross-low, cross-high, cross-sum) = FIND-MAXIMUM-CROSSING-SUBARRAY(A, low, mid, high)
7 if left-sum ≥ right-sum and left-sum ≥ cross-sum
8 return (left-low, left-high, left-sum)
9 elseif right-sum ≥ left-sum and right-sum ≥ cross-sum
10 return (right-low, right-high, right-sum)
11 else return (cross-low, cross-high, cross-sum)- 줄 3-11이 재귀 명제 처리.
- 줄 3에서 분할. A[low…mid]를 좌부분열 left subarray, A[mid + 1…high]를 우부분열 right subarray라 칭함.
- 줄 4, 5에서 정복
- 줄 6-11에서 결합
분할정복 알고리듬 분석
문제의 크기가 2의 제곱수라 가정. 줄 1은 상수 시간. n = 1일 때, 즉 바탕 명제일 땐 줄 2에서 상수 시간. 그러므로:
T(1) = Θ(1).
줄 4, 5의 부분열의 크기는 n/2. 즉 각각 T(n/2) 시간. 줄 6의 FIND-MAX-CROSSING-SUBARRAY는 Θ(n). 줄 7-11은 Θ(1).
T(n) = Θ(1) + 2T(n/2) + Θ(n) + Θ(1)
= 2T(n/2) + Θ(n)
T(n) =
- Θ(1) (n = 1일 경우)
- 2T(n/2) + Θ(n) (n > 1일 경우)
즉, T(n) = Θ(n log2 n)
주먹구구식보다 분할정복법이 더 빠른 알고리듬을 만들어 줌. 연습문제 4.1-5에서도 보겠지만 최대 부분열 문제는 선형 시간 내에 해결 가능.
4.2. 슈트라센 알고리듬을 통한 행렬곱
행렬곱 공식. 행렬의 각 원소 cij의 공식:
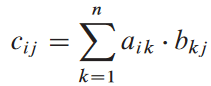
n2 개의 원소가 있음.
SQUARE-MATRIX-MULTIPLY(A, B)
1 n - A.rows
2 C가 새로운 n × n 행렬
3 for i = 1 to n
4 for j = 1 to n
5 c_ij = 0
6 for k = 1 to n
7 c_ij = c_ij + a_ik ⋅ b_kj
8 return C- 줄 3-7: 각 i 번째 열 연산
- 줄 4-7: i 번째 열의 각 j 번째 행에 대해 cij 연산.
for문이 삼중첩이므로 SQUARE-MATRIX-MULTIPLY은 Θ(n3) 만큼의 시간이 걸림.
애초에 곱셈이 많으니 Ω(n3) 걸린다고 생각할 수 있는데, o(n3) 시간에 곱셈 가능. 슈트라센의 재귀 알고리듬 사용하면 Θ(nlog 7) 걸림. log 7은 2.80에서 2.81 사이. 즉, 슈트라센 알고리듬은 O(n2.81) 걸림.
간단한 분할정복 알고리듬
n이 2의 제곱수라 가정. n × n 행렬을 네 개의 n / 2 × n / 2 행렬로 분할. n ≥ 2인 이상 n / 2 차원은 정수.
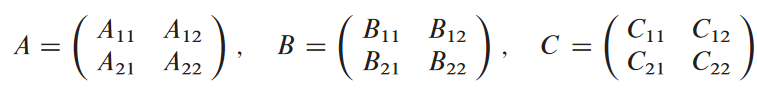
위의 행렬 A, B, C를 사분할해서 C = A ⋅ B을 다음과 같이 재작성 한다 가정.
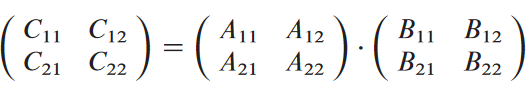
그럼 다음 네 개의 방정식으로 나뉨:
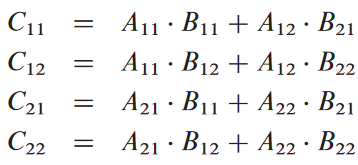
이걸로 간단한 재귀적 분할정복 알고리듬 만들기 가능:
SQUARE-MATRIX-MULTIPLY-RECURSIVE(A, B)
1 n = A.rows
2 C가 새로운 n × n 행렬
3 if n == 1
4 c_11 = a_11 ⋅ b_11
5 else A, B, C를 위에서 처럼 분할
6 C_11 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A_11, B_11)
+ SQUARE-MATRIX-MULTIPLY-RECURSIVE(A_12, B_21)
7 C_12 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A_11, B_12)
+ SQUARE-MATRIX-MULTIPLY-RECURSIVE(A_21, B_22)
8 C_21 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A_21, B_11)
+ SQUARE-MATRIX-MULTIPLY-RECURSIVE(A_22, B_21)
9 C_22 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A_21, B_12)
+ SQUARE-MATRIX-MULTIPLY-RECURSIVE(A_22, B_22)
10 return C여기서 문제는 줄 5에서 분할법. 12 개의 n / 2 × n / 2 행렬 만드는 건 복사하는 데만 Θ(n2). 그래서 복사하지 말고 색인 활용. 그러면 Θ(1)에 가능.
SQUARE-MATRIX-MULTIPLY-RECURSIVE의 실행 시간 분석하자면, 바탕 명제에서 줄 4에 T(1) = Θ(1).
재귀 명제에서 줄 5는 색인 계산법 사용해서 Θ(1), 줄 6-9에서 재귀적으로 총 여덟번 호출하니까 8T(n / 2). 줄 6-9의 네번의 행렬 덧셈에서 각 행렬은 n2 / 4 개의 원소를 가지니 Θ(n2) 시간. 총 덧셈 수는 상수 개니 줄 6-9은 총 Θ(n2) 시간. (이때 색인 계산법으로 결과값도 올바른 위치에 넣어야 하니 각 원소별로 Θ(1)의 오버헤드 발생.)
T(n) = Θ(1) + 8T(n/2) + Θ(n2)
= 8T(n/2) + Θ(n2)
바탕 명제랑 같이 표기하면:
T(n) =
- Θ(1) (n = 1일 경우)
- 8T(n/2) + Θ(n2) (n > 1일 경우)
4.5 단원에 마스터 정리에서도 보겠지만 이 점화식의 해답은 T(n) = Θ(n3). 분할정복법이라고 해서 SQUARE-MATRIX-MULTIPLY보다 더 빠르고 간단하지는 않음.
여기서 명심해야하는 건 점근 표기법 앞의 계수는 무시할 수 있어도 T(n/2)과 같은 재귀 표기법 앞의 계수는 무시 못 함.
슈트라센법
슈트라센법의 핵심은 재귀 트리를 덜 부시시하게 만드는 것. n / 2 × n / 2 행렬곱을 여덟번이 아니라 일곱번으로 줄이는 것.
슈트라센법이 직관적으로 이해하기 쉬운 건 아님. 네 가지 단계 존재:
- 입력 행렬 A, B, 그리고 출력 행렬 C 세 가지를 n / 2 × n / 2 행렬로 사분할. 색인 계산법으로 Θ(1) 시간.
- 10 개의 행렬 S1, S2, …, S10 생성. 각각 1 단계에서 사분할한 n / 2 × n / 2 행렬들의 합 또는 차임. 10 개 전부 Θ(n2) 시간에 생성 가능.
- 1 단계에서 만든 부분행렬과 2 단계에서 만든 10 개의 행렬들로 재귀적으로 일곱 개의 행렬곱 P1, P2, …, Pn 계산. 각 행렬 Pi는 n / 2 × n / 2.
- Pi를 더하거나 빼는 식으로 조합하여 결과 행렬 C의 부분행렬 C11, C12, C21, C22 계산. Θ(n2) 시간.
기존 방법과 동일하게 행렬의 크기 n이 1이 될 때 스칼라 곱셈 행한다고 가정. n > 1일 때 1, 2, 4 단계는 총 Θ(n2) 시간. 단계 3은 7번의 n / 2 × n / 2 행렬간 곱. 슈트라센 알고리듬의 실행 시간 T(n)에 대한 점화식:
T(n) =
- Θ(1) (n = 1일 경우)
- 7T(n/2) + Θ(n2) (n > 1일 경우)
마스터 정리에 의해 위의 점화식의 해답은 T(n) = Θ(nlog 7).
단계 2에서 10 개의 행렬은 다음과 같이 생성:
- S1 = B12 - B22
- S2 = A11 + B12
- S3 = A21 + A22
- S4 = B21 - B11
- S5 = A11 + B22
- S6 = B11 + B22
- S7 = A12 - A22
- S8 = B21 + B22
- S9 = A11 - B21
- S10 = B11 + B12
이 단계는 Θ(n2).
단계 3에서 n / 2 × n / 2 행렬 일곱번 곱해서 새로운 n / 2 × n / 2 행렬 만듦:
- P1 = A11 ⋅ S1 = A11 ⋅ B12 - A11 ⋅ B22
- P2 = S2 ⋅ B22 = A11 ⋅ B22 + A12 ⋅ B22
- P3 = S3 ⋅ B11 = A21 ⋅ B11 + A22 ⋅ B11
- P4 = A22 ⋅ S4 = A22 ⋅ B21 - A22 ⋅ B11
- P5 = S5 ⋅ S6 = A11 ⋅ B11 + A11 ⋅ B22 + A22 ⋅ B11 + A22 ⋅ B22
- P6 = S7 ⋅ S8 = A12 ⋅ B21 + A12 ⋅ B22 - A22 ⋅ B21 - A22 ⋅ B22
- P7 = S9 ⋅ S10 = A11 ⋅ B11 + A11 ⋅ B12 - A21 ⋅ B11 - A21 ⋅ B12
결국 실질적으로는 두번째 항의 곱셈만 하면 됨.
4 단계에서 Pi 행렬들을 더하고 빼서 결과 C를 구함.
- C11 = P5 + P4 - P2 + P6
- C12 = P1 + P2
- C21 = P3 + P4
- C22 = P5 + P1 - P3 - P7
이 단계도 Θ(n2) 시간 걸림.
이 점화식의 결과는 T(n) = Θ(nlog 7)이므로 기존 방법보다 점근적으로 빠름.
4.3. 치환법을 통한 재귀 풀기
점화식이 분할정복 알고리듬의 실행 시간을 구하는데 사용됨을 알았으니 이제 점화식 푸는 방법 배울 것.
치환법 substitution method은 두 단계로 나뉨:
- 공식을 추측
- 수학적 귀납법으로 상수를 찾고, 공식이 맞음을 보임
우리가 추측한 공식과 구하려는 함수를 치환하기 때문에 "치환법"이라 부름. 매우 강력한 방법이지만 추측할 줄 알아야 함.
T(n) = 2T(⌊n/2⌋) + n에 대해서 찍기를 한다고 가정. 대충 T(n) = O(n log n)겠거니 하고 찍기. 그러면 적당한 상수 c > 0에 대해 T(n) ≤ cn log n임을 증명해야 함. 이 유계가 m < n인 모든 양수, 특히 m = ⌊n/2⌋일 때에 대해 적합하다고 가정. 그러면 T(n) ≤ c⌊n/2⌋ log (⌊n/2⌋).
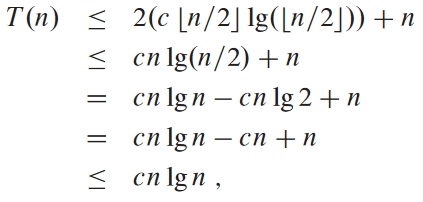
이제 유계 조건 만족함을 보여야 함. 보통은 바탕 명제에 만족함을 귀납적 증거를 위해 보이면 됨. 이때 유계 T(n) ≤ cn log n가 유계 조건에 만족하도록 적당히 큰 상수 c를 골라야 함. 예를 들어 T(1) = 1가 유일한 유계라고 할 때 n = 1일 때 T(n) ≤ cn log n는 T(1) ≤ 0이 되므로 맞지 않으니 바탕 명제가 거짓이 됨.
이거 해결하려면 특정 유계 조건에 대한 귀납적 추론을 증명해주면 됨. 예를 들어 우리가 고를 수 있는 상수 n0에 대해 n ≥ n0를 만족하는 T(n) ≤ cn log n를 증명하면 됨. T(1) = 1라는 유계는 잊고, n > 3부터 보도록. 이제 바탕 명제는 T(1), T(2), T(3). 물론 당연히 점화식의 바탕 명제 T(1)와 귀납적 증명을 위한 바탕 명제 T(2)와 T(3)는 구분해야 함. T(1) = 1일 때 T(2) = 4와 T(3) = 5이므로, c ≥ 2일 때 이 바탕 명제가 참임을 알 수 있음. 우리가 볼 대부분의 점화식에선 유계 조건을 확장하여 귀납적 추론이 작은 n에서도 만족함을 간단하게 보일 수 있음.
좋은 추측하는 법
일반적인 방법은 없음. 경험이랑 창의성 필요.
점화식이 전에 본 거랑 비슷하면 그거랑 비슷한 추측하는 건 나름 합리적임.
또다른 방법으로는 대충 상한 / 하한일 것 같은 걸 대입해보고 범위를 줄여가는 것임.
세부 사항
점화식의 해법에 대한 점근 유계를 제대로 찍었을 수도 있는데, 귀납법에서 오류가 날 수도 있음. 찍기로는 충분한 유계를 제시하기엔 불충분하다는 것.
이게 귀납법이 틀렸다고 해서 다시 찍으라는 게 아니고, 귀납법을 적용하는 방법을 바꿔보면 됨. 찍은 답보다 차수가 낮은 항을 빼주는 것으로 해결 가능. T(n) = O(n)라 찍었을 때 이게 귀납법에서 실패하면 T(n) = O(n2)로 가는 게 아니라, d ≤ 0이 상수일 때 T(n) ≤ cn - d로 새로 찍어서 귀납법에 다시 맞추는 것.
함정 피하기
점근 표기법 사용할 때 자주 발생하는 오류. T(n) = O(n)을 증명하겠다고 T(n) ≤ cn라고 찍은 다음
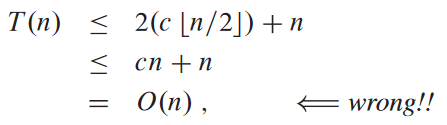
위와 같다고 우기는 것임. 문제는 귀납적 추론의 정확한 식, 즉 T(n) ≤ cn을 증명하지 않았다는 것. 그러므로 T(n) = O(n)임을 보일 때 T(n) ≤ cn를 명시적으로 증명해야 함.
변수 바꾸기
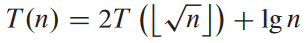
위의 점화식을 m = log2 n라고 변수를 바꿔서 표현하면:
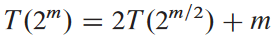
여기서 S(m) = T(2m)이라 가정:
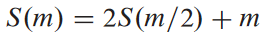
S(m) = O(m log2 m)이므로
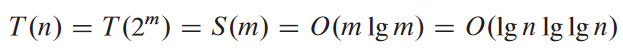
4.4. 재귀 트리법을 통한 재귀 풀기
솔직히 찍는 건 어려움. 그래서 재귀 트리를 직접 그리면 찍기가 좀 더 쉬워짐. 재귀 트리 recursion tree에서 각 노드는 언젠가 실행될 재귀 함수의 집합 중 한 하위 문제의 비용을 의미함. 각 트리의 층마다 비용을 합쳐서 층당 비용을 구함. 이 층당 비용을 더해서 재귀의 총 비용을 구함.
예시: T(n) = 3T(⌊n/4⌋) + Θ(n2).
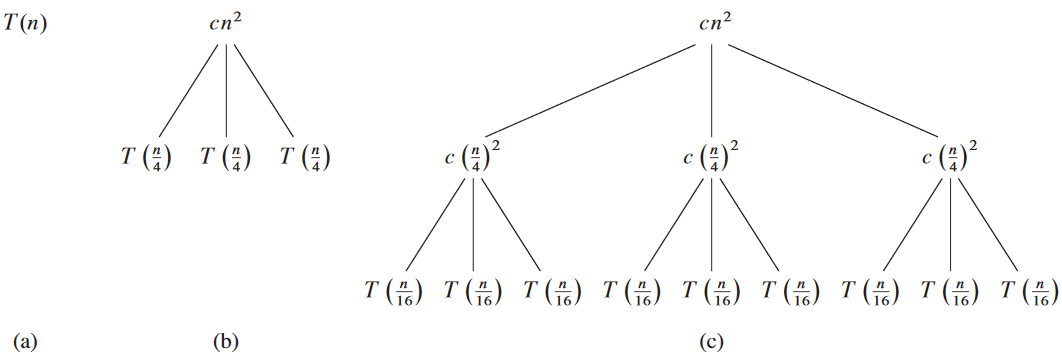
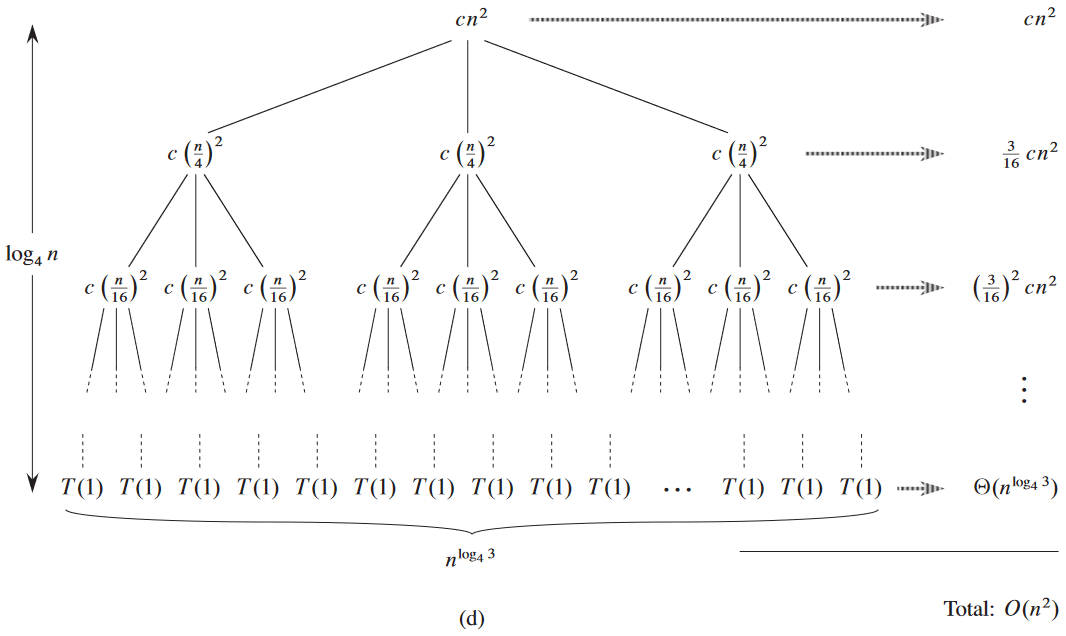
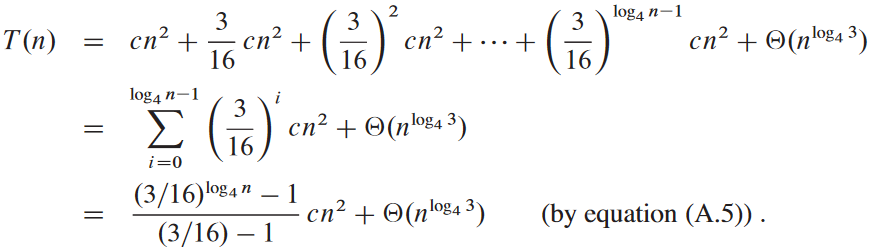
마지막 생긴 거 딱 보니까 무한대로 감소하는 기하학적 수열을 상계로 삼고 싶게 생김.
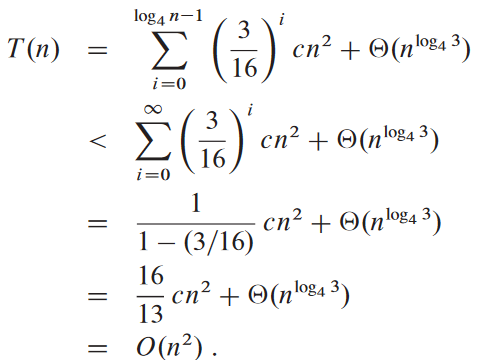
여기서 볼 수 있듯, 잎들이 전체 비용의 대부분을 차지함.
O(n2)이 상한은 맞음. 그러면 이게 좁은 유계여야 함. 첫번째 재귀 호출이 Θ(n2) 만큼 차지하므로 점화식의 하계가 Ω(n2)이어야 함.
이제 치환법으로 제대로 잘 찍었는지 증명해야 함. 어떤 상수 d > 0에 대해 T(n) ≤ dn2 만족하는 지 확인.
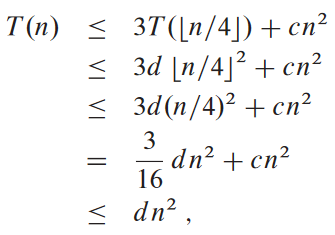
d ≥ (16/13)c라면 마지막 단계가 참임.
새로운 예시:
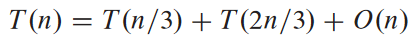
이 예시의 재귀 트리:
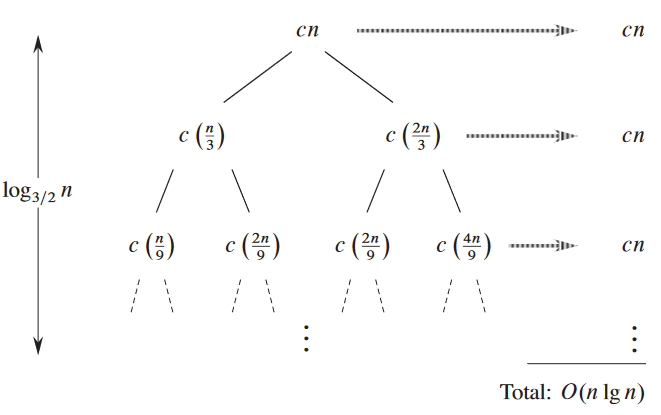
치환법으로 증명하기:
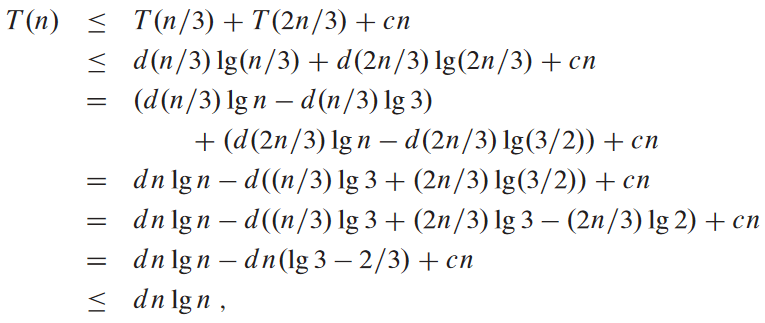
4.5. 마스터 정리를 통한 재귀 풀기
마스터 정리는 아래 형태의 점화식 푸는 "레시피" 제공.
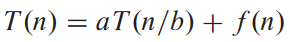
여기서 상수 a ≥ 1, b > 1가 존재, 그리고 f(n) 점근적 양인 함수. 이거 사용하려면 세 가지 경우 외워야 함.
위의 문제는 크기 n의 문제를 a 개의 크기 n/b인 하위 문제로 분할함. f(n)은 하위 문제로의 분할과 결합 비용에 대한 함수. 슈트라센 알고리듬의 경우 a = 7, b = 2, f(n) = Θ(n2)
참고로 이건 엄밀한 정의가 아님 n/b가 정수가 아닐 수 있으니. 그러므로 바닥/천장 함수로 넣어줘야 점근적 행동방식에 영향 안 줌. 근데 귀찮으니까 ㅎㅎ.
마스터 정리
마스터 정리에 사용할 정리들:
정리 4.1 (마스터 정리)
a ≥ 1, b > 1가 상수고, f(n)가 함수고, T(n)가 비음 정수에 대한 점화식으로 정의:
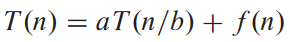
여기서 n/b란 ⌊n/b⌋, ⌈n/b⌉ 둘 중 하나. T(n)은 다음과 같은 점근 유계 가짐:
- 어떤 상수 ε > 0에 대해 f(n) = O(nlogb a - ε)일 경우 T(n) = Θ(nlogb a)
- f(n) = Θ(nlogb a)일 경우 T(n) = Θ(nlogb alog2 n)
- 어떤 상수 ε > 0에 대해 f(n) = Ω(nlogb a + ε)이고, 어떤 상수 c < 1, 그리고 충분히 큰 n 대해 af(n/b) ≤ cf(n)일 경우 T(n) = Θ(f(n))
이해를 해보자면 셋 다 f(n)을 함수 nlogb a와 비교. 둘 중 더 큰게 점화식의 해답을 결정할 것. 첫번째 경우에서 함수 nlogb a이 더 크다면 해답은 T(n) = Θ(nlogb a). 세번째 경우에서 함수 f(n)이 더 클 경우 해답은 T(n) = Θ(f(n)), 두번째의 경우 둘이 같다면 해답은 T(n) = Θ(nlogb alog2 n) = Θ(f(n)log2 n).
세부 사항에도 주목해야 함. 첫번째 경우 f(n)이 단순히 nlogb a보다 작아야 하는 게 아니라 다항적으로 작아야 함. 즉, nlogb a보다 어떤 상수 ε > 0에 대해 nε의 인수만큼 점근적으로 작아야 함. 세번째도 마찬가지로 다항적으로 커야하며 거기다 af(n/b) ≤ cf(n)라는 "제일성" 조건도 만족해야 함. 대부분의 다항적 유계 함수가 이 조건을 만족함.
이 세 가지 경우가 f(n)에 대한 모든 경우를 처리하는 건 아님. 이러한 나머지 경우에 해당하거나 세번째 경우에서 제일성 조건을 만족하지 않는다면 점화식 풀 때 마스터 정리 사용 못 함.
마스터 정리 사용하기
어떤 경우에 해당하는지 우선 찾아야 함.
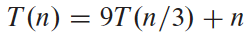
위의 점화식의 경우 nlogb a = nlog3 9 = Θ(n2). ε = 1일 때 f(n) = O(nlog3 9 - ε)이므로 첫번째 경우 적용하여 T(n) = Θ(n2)임을 알 수 있음.
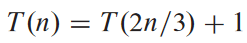
위의 점화식의 경우 nlogb a = nlog3/2 1 = n0 = 1. f(n) = Θ(nlogb a) = Θ(1)이므로 두번째 경우 적용하여 T(n) = Θ(log2 n)임을 알 수 있음.
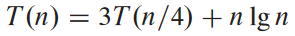
위의 점화식의 경우 nlogb a = nlog4 3 = O(n0.793). ε ≈ 0.2일 때 f(n) = Ω(nlog4 3 + ε)이므로 세번째 경우 적용하여 제일성 조건 확인. 충분히 큰 n에 대해 c = 3/4일 때 af(n/b) = 3(n/4) log2 (n/4) ≤ (3/4)n log2 n임. 그러므로 세번째 경우에 의해 T(n) = Θ(n log2 n)임을 알 수 있음.
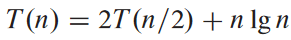
얘의 경우에서 f(n) = n log2 n이 nlogb a = n보다 점근적으로 크다고 해서 세번째 경우에 해당한다고 생각할 수도 있는데, 얘 다항적으로 크진 않음. 비율 f(n)/nlogb a = n log2 n / n = log2 n은 임의의 양수인 상수 ε에 대해 nε보다 점근적으로 작음. 그러므로 두번째와 세번째 경우의 사이에 해당함.
