중간에 5편인 확률적 분석 및 무작위 알고리듬은 스킵했습니다.
6. 힙 정렬
합병정렬처럼 O(n lg n)임.
"힙"이라는 자료구조 사용해서 정보 관리. 힙 정렬에 있어 힙이 제일 유용할 뿐만 아니라 효율적인 우선순위 큐 만드는데 좋음.
"힙"이 원래 힙 소트에서 온 거긴 한데, "가비지 컬렉터 저장소"로도 사용하는 표현인데, 여기서는 자료구조 힙으로서의 의미를 사용.
6.1. 힙
(이진) 힙 (binary) heap은 완전 이진 트리와 유사하게 볼 수 있는 배열로 된 자료구조.
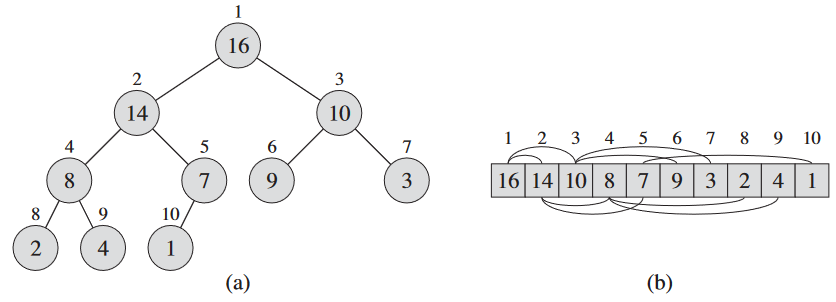
PARENT(i)
1 return ⌊i/2⌋LEFT(i)
1 return 2iRIGHT(i)
1 return 2i + 1두 가지 이진 힙: 최대 힙과 최소 힙. 둘 다 노드들이 힙 속성 heap property을 만족해야 함. 최대 힙 max-heap의 최대 힙 속성 max-heap property은 루트가 아닌 모든 노드 i에 대해서
A[PARENT(i)] ≥ A[i]를 만족. 즉, 노드의 값은 부모의 값보다 작거나 같음. 즉, 최대값은 언제나 루트 노드. 최소 힙 min-heap은 반대임. 최소 힙 속성 min-heap properties에서는 루트 노드가 아닌 모든 노드 i에 대해서
A[PARENT(i)] ≤ A[i]를 만족. 루트가 최소값.
힙 정렬 알고리듬에서는 최대 힙 사용. 최소 힙으로는 보통 우선순위 큐를 구현. 최대나 최소 중 특정이 되는 건 말을 할 건데, 그게 아니라면 앞으로 "힙"이라는 표현은 둘 다 가능함을 의미.
힙을 트리로 보면 우선 노드의 높이 height를 노드에서 잎으로 단순히 직진했을 때의 최대 거리로 정의하고, 힙의 높이는 루트의 높이라 표현. 힙은 완전 이진 트리 기반이니까 원소가 n 개면 그 높이는 Θ(lg n). 힙의 기본적인 연산들은 최대 힙의 높이와 비례하므로 O(lg n) 걸림. 여기서 몇 가지 기본적인 함수 소개:
MAX-HEAPIFY함수, O(lg n). 최대 힙 속성 유지.BUILD-MAX-HEAP함수, 선형 시간. 비정렬 입력 배열로부터 최대 힙 생성.HEAPSORT함수, O(n lg n). 배열을 정렬.MAX-HEAP-INSERT,HEAP-EXTRACT-MAX,HEAP-INCREASE-KEY,HEAP-MAXIMUM함수, O(lg n). 힙 자료구조로 우선순위 큐 구현 가능하게 해줌.
6.2. 힙 속성 유지하기
힙 속성 유지하는 함수가 MAX-HEAPIFY 함수. 배열 A랑 배열의 색인 i를 입력으로 받음. 호출되면 LEFT(i)와 RIGHT(i)을 루트로 삼는 이진 트리가 최대 힙이 되야 한다고 가정함. 이때 A[i]는 자기 자식보다 작을 수 있어 최대 힙 속성을 위반함. MAX-HEAPIFY는 A[i]의 값을 일종의 "가라 앉게" 만들어서 색인 i를 루트 삼은 부분트리가 최대 힙 속성을 갖게 함.
MAX-HEAPIFY(A, i)
1 left = LEFT(i)
2 right = RIGHT(i)
3 if left ≤ A.heap-size and A[left] > A[i]
4 largest = left
5 else largest = left
6 if right ≤ A.heap-size and A[right] > A[largest]
7 largest = right
8 if largest ≠ i
9 exchange A[i] with A[largest]
10 MAX-HEAPIFY(A, largest)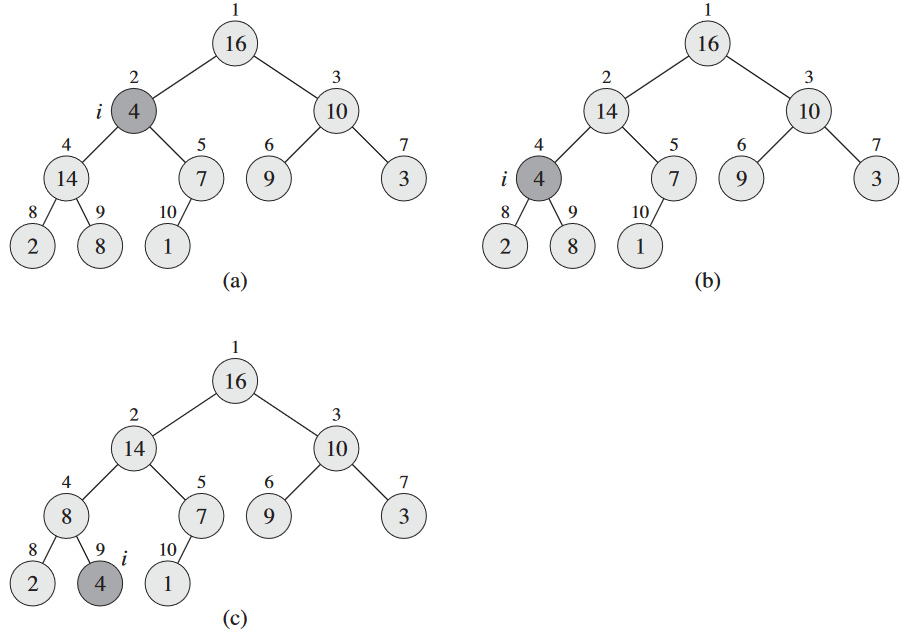
MAX-HEAPIFY 함수의 시간 복잡도: A[i], A[LEFT(i)], A[RIGHT(i)] 간 관계 수정에 Θ(1), 노드 i의 자식의 부분열에서 작동할 MAX-HEAPIFY (재귀 호출이 된다면). 자식의 부분트리의 크기는 최대 2n/3. 최악의 경우는 트리의 맨 아래 층이 반만 가득 차있을 때.
T(n) ≤ T(2n/3) + Θ(1)
마스터 정리에 의해 T(n) = O(lg n). 높이를 h 삼아 O(h)라고 표현하기도.
6.3. 힙 만들기
MAX-HEAPIFY를 상향식으로 바꿔서 배열 A[1..n]를 최대 힙으로 바꿔줄 수 있음.
BUILD-MAX-HEAP(A)
1 A.heap-size = A.length
2 for i = ⌊A.length/2⌋ downto 1
3 MAX-HEAPIFY(A, i)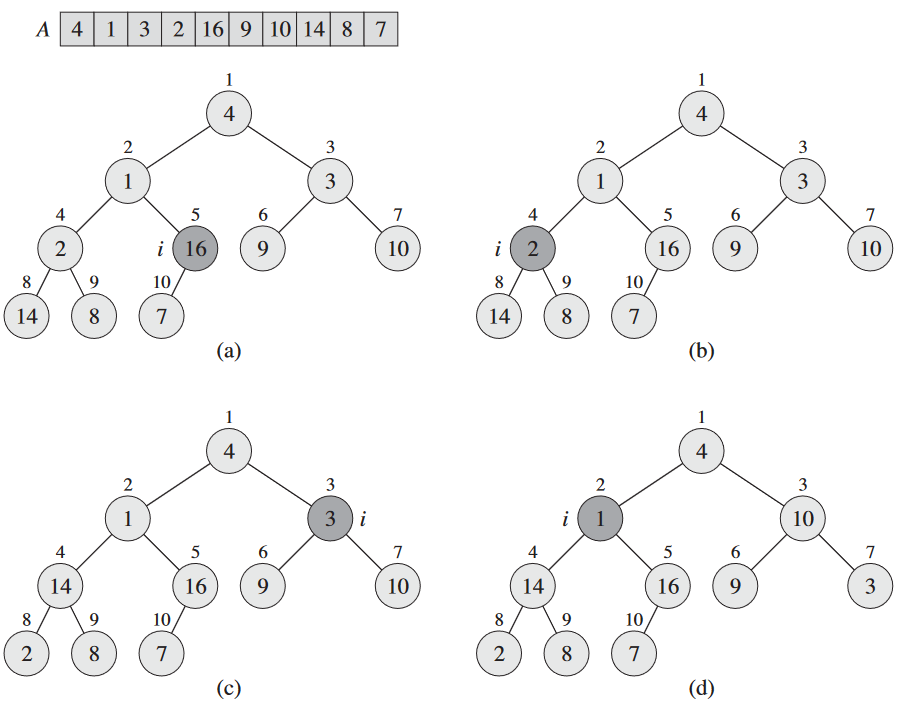
BUILD-MAX-HEAP이 제대로 동작함을 보이기 위해 다음 루프 불변성을 사용:
2-3번 줄의
for루프의 각 반복의 시작마다 각 i + 1, i + 2, …, n 번째 노드가 최대 힙의 루트가 됨.
- 초기화: 루프 첫 실행 이전에 i = ⌊n/2⌋. 각 ⌊n/2⌋ + 1, ⌊n/2⌋ + 2, …, n 번째 노드는 잎이므로 최대 힙의 루트가 됨이 자명함.
- 유지: i 번째 노드의 자식이 i보다 숫자가 크면 각 반복마다 루프 불변성이 유지되는 것. 그러면 불변성에 의해 둘 다 최대 힙의 루트가 됨. 이게 바로
MAX-HEAPIFY(A, i)를 통해 i 번째 노드를 최대 힙으로 만들어주는 단계. 이때 각 i + 1, i + 2, …, n 번째 노드가 최대 힙의 루트가 된다는 성질도 유지됨.for루프에서 i를 감소시키면 다음 반복을 위한 불변성을 재설정해줌. - 종료:종료 시 i = 0임. 불변성에 의해 각 1, 2, …, n 번째 노드가 최대 힙의 루트임.
간단하게 상계 계산. 각 MAX-HEAPIFY(A, i) 호출마다 O(lg n). BUILD-MAX-HEAP(A)은 이걸 O(n)번 호출. 즉, 실행 시간 O(n lg n). 점근적으로 좁진 않을 수 있음.
더 좁은 상계 구하려면 트리의 높이에 따라 계산해야 함. 원소가 n 개인 힙의 높이는 ⌊lg n⌋이고 임의의 높이 h에 대해 최대 ⌈n/2h + 1⌉ 개의 노드들.
MAX-HEAPIFY(A, i) 호출할 때 높이 h인 노드에 대해 O(h).
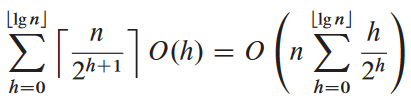
이므로, 마지막 식을 다음으로 표현
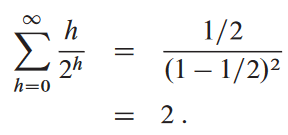
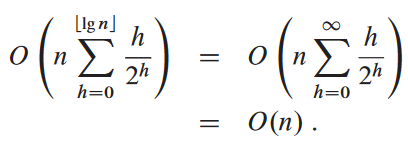
즉, 비정렬 배열로부터 최대 힙을 선형 시간 내에 만들 수 있음.
6.4. 힙 정렬 알고리듬
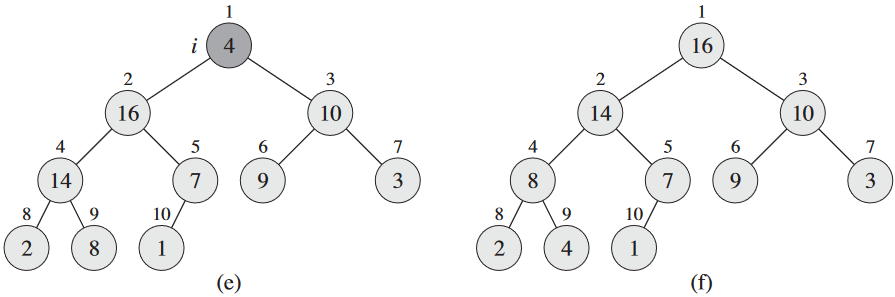
우선 BUILD-MAX-HEAP으로 입력 배열 A[1..n]을 최대 힙으로 치환. 최대값이 A[1]에 있으니 A[n]이랑 교체해주면 됨. 이제 A.heap-size 감소시켜서 n 번째 노드 무시하고 자식들을 처리하면 되는데, 얘네가 최대 힙 속성을 만족 안 할 수도. 그래서 `MAX-HEAPIFY(A, 1)를 통해 최대 힙 속성 복구하면 A[1..n-1]에 최대 힙 남음. 이걸 힙 크기가 n - 1에서 2까지 반복하면 됨.
HEAPSORT(A)
1 BUILD-MAX-HEAP(A)
2 for i = A.length downto 2
3 exchange A[1] with A[i]
4 A.heap-size = A.heap-size - 1
5 MAX-HEAPIFY(A, 1)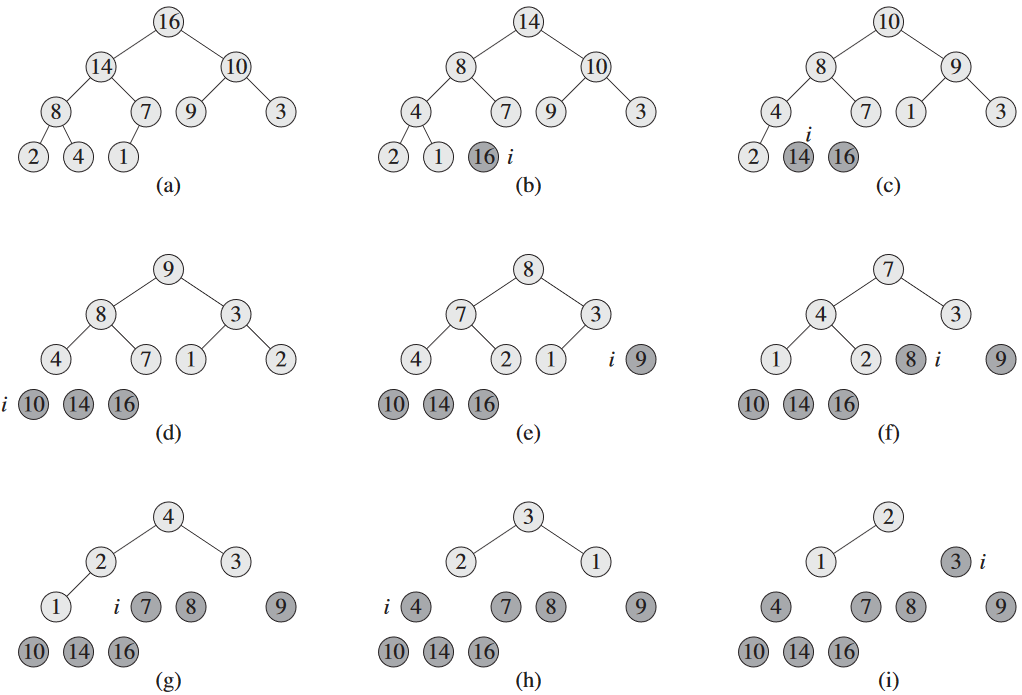
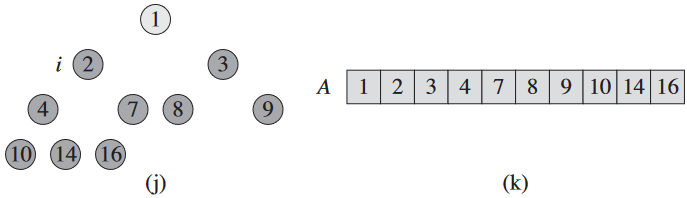
BUILD-MAX-HEAP에 O(n), MAX-HEAPIFY가 각각 O(lg n) 걸리는데, 이걸 n - 1번. 즉, HEAPSORT는 O(n lg n).
6.5. 우선순위 큐
힙 정렬도 좋긴 한데 퀵 정렬에 비하면 좀 느림. 그래서 잘 안 쓰는데, 그래도 힙이 사용되는 곳이 있으니, 바로 효율적인 우선순위 큐임. 힙처럼 두 가지 종류: 최대 우선순위 큐랑 최소 우선순위 큐. 여기서는 최대 힙에 기반한 최대 우선순위 큐 설명.
우선순위 큐 priority queue란 키 key라는 값을 갖는 원소들의 집합 S를 유지하는 자료구조임. 최대 우선순위 큐 max-priority queue는 다음 연산 지원:
INSERT(S, x). 집합 S에서 원소 x 삽입. 즉 S = S ∪ {x}MAXIMUM(S). 최대 키를 갖는 집합 S의 원소 반환.EXTRACT-MAX(S). 최대 키를 갖는 집합 S의 원소를 제거하고 반환.INCREASE-KEY(S, x, k). 원소 x의 키를 k의 값(원래 값보다 크거나 같음)으로 증가.
최대 우선순위 큐로 공유 컴퓨터의 일을 스케줄링하는 데 사용. 최대 우선순위 큐는 실행해야 할 일들과 이들의 상대적 우선순위를 가짐. 일이 끝나거나 인터럽트가 발생하면 스케줄러는 EXTRACT-MAX로 최고 우선순위를 갖는 일을 선택. INSERT로 언제든 새 일을 큐에 추가 가능.
반대로 최소 우선순위 큐 min-property queue는 INSERT, MINIMUM, EXTRACT-MIN, DECREASE-KEY 연산을 지원. 이벤트 기반 시뮬레이터에 사용 가능. 큐에 있는 원소들은 발생 시간을 키로 삼음. 발생 시간 순으로 시뮬레이션 되야 하니까.
힙으로 우선순위 큐를 구현. 어플리케이션의 어떤 개체가 주어진 우선순위 큐의 원소에 해당하는 지를 결정해야 함. 힙으로 우선순위 큐를 구현한다면 각 힙 원소의 어플리케이션 개체에 대응하는 핸들 handle이 필요. 핸들이 어떻게 생겨먹었는지(포인터? 정수?)는 어플리케이션 개체에 달려있음. 또한 각 어플리케이션 개체 안의, 핸들에 대응하는 힙 원소에 핸들을 저장해야 함. 보통은 배열 색인을 사용. 힙 원소들이 연산 중 배열 내부에서 위치가 바뀔 수 있으므로 실제 구현할 때는 힙 원소를 재할당할 때 대응하는 어플리케이션 개체에 대한 배열 색인도 갱신해줘야 함.
HEAP-MAXIMUM 함수는 MAXIMUM 연산을 Θ(1) 시간에 구현
HEAP-MAXIMUM(A)
1 return A[1]HEAP-EXTRACT-MAX 함수는 EXTRACT-MAX 연산을 구현. HEAPSORT 함수의 for문 본문(3-5번 줄)과 유사.
HEAP-EXTRACT-MAX(A)
1 if A.heap-size < 1
2 error "heap underflow"
3 max = A[1]
4 A[1] = A[A.heap-size]
5 A.heap-size = A.heap-size - 1
6 MAX-HEAPIFY(A, 1)
7 return maxO(lg n). MAX-HEAPIFY의 O(lg n)에 대해 상수 시간만큼 실행.
HEAP-INCREASE-KEY 함수는 INCREASE-KEY 연산을 구현. i가 우리가 증가시킬 우선순위 큐의 원소에 대한 배열 색인. 우선 A[i]의 값을 증가시키고, 이게 최대 힙 속성 위배할 수도 있으니 2.1절의 INSERTION-SORT의 삽입 루프(5-7번 줄)에서처럼 이 노드에서 루트까지 새롭게 증가된 키의 올바른 위치 찾음. 이때 반복적으로 자기 부모와 값을 비교하여, 원소의 키가 더 크면 교체하고, 아니라면 최대 힙 속성을 만족하므로 종료함.
HEAP-INCREASE-KEY(A, i)
1 if key < A[i]
2 error "new key is smaller than current key"
3 A[i] = key
4 while i > 1 and A[PARENT(i)] < A[i]
5 exchange A[i] with A[PARENT(i)]
6 i = PARENT(i)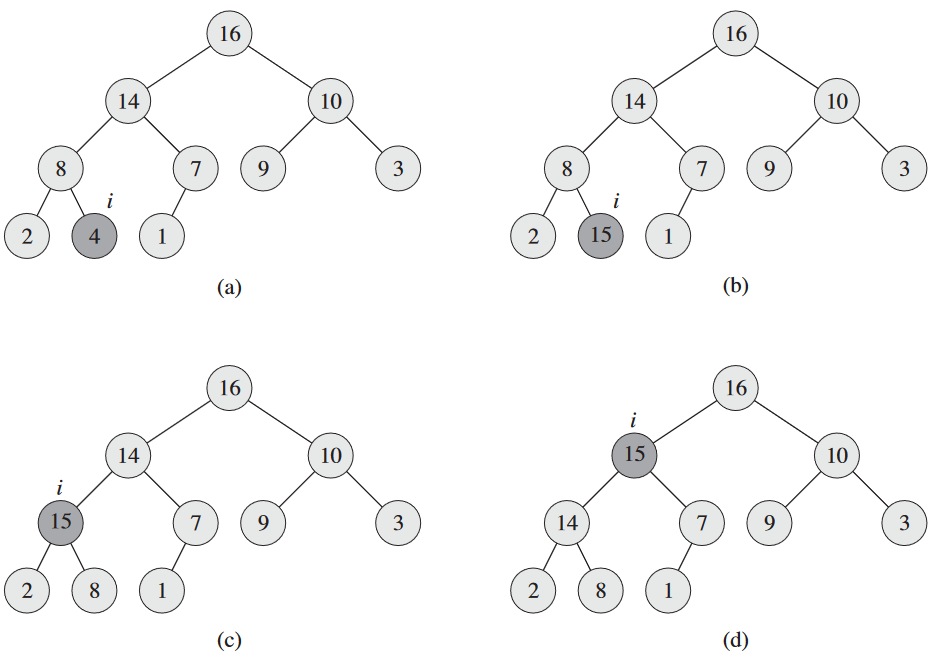
HEAP-INCREASE-KEY는 O(lg n). 3번 줄에서 갱신한 노드에서 루트까지의 경로의 길이가 O(lg n)이니까.
MAX-HEAP-INSERT 함수는 INSERT 연산을 구현. 우선 트리에 키가 -∞인 새 원소 추가. 그 다음에 HEAP-INCREASE-KEY로 이 노드의 키를 추가하려는 값으로 수정해주고 최대 힙 속성을 유지해줌.
MAX-HEAP-INSERT(A, key)
1 A.heap-size = A.heap-size + 1
2 A[A.heap-size] = -∞
3 HEAP-INCREASE-KEY(A, A.heap-size, key)MAX-HEAP-INSERT는 O(lg n).
힙은 모든 우선순위 큐의 연산을 O(lg n)에 수행.
