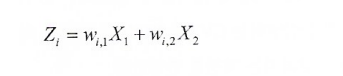
7.1 주성분분석
1. 용어 정리
- 주성분(principal component): 예측변수들의 선형결합
- 부하(loading): 예측변수들을 성분으로 변형할 때 사용되는 가중치
- 스크리그래프(screeplot): 성분들의 변동을 표시한 그림. 설명된 분산 혹은 설명된 분산의 비율을 이용하여 성분들의 상대적인 중요도를 보여준다.
2. 주성분분석 이란?
- 주성분분석(PCA): 수치형 변수가 어떤 식으로 공변하는지 알아내는 기법
- 주성분: 전체 변수들의 변동성을 거의 대부분 설명할 수 있는 적은 수의 변수들의 집합
- 활용성: 데이터 차원 축소
7.1.1 간단한 예제
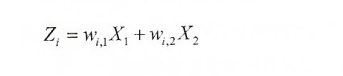
- Z: 주성분
- X: 변수
- w: 가중치 (= 주성분의 부하)
- Z1: 전체 변동성을 가장 잘 설명하는 선형결합
- Z2: 첫 주성분과 서로 수직이며, 나머지 변동성 설명
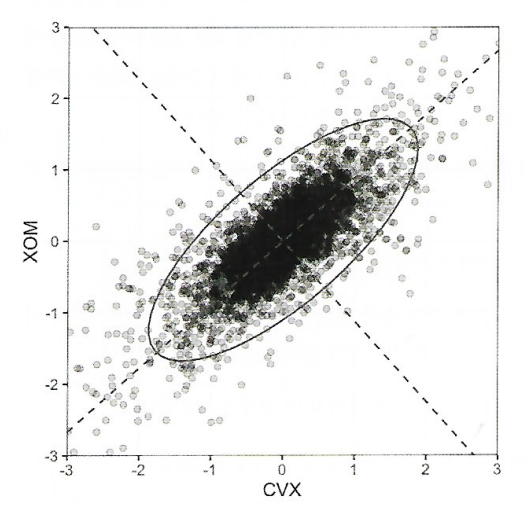
셰브런(CVX)과 엑스모빌(XOM)의 주가 수익에 대한 주성분
- 두 점선은 각각 주성분의 방향을 보여준다.
- 첫 번째 선은 타원의 장축을 따라 존재
- 두 번째 선은 단축 위에 존재
7.1.2 주성분 계산
- 첫 번째 주성분을 구하기 위해 PCA는 전체 변동을 최대한 설명하기 위한 예측변수의 선형결합을 구한다.
- 이 선형결합은 첫 번째 새로운 예측 수 Z1이 된다.
- 같은 변수들을 이용해 새로운 두 변수 Z2를 만들기 위해, 다른 가중치를 가지고 이 과정을 반복하다. 가중치 Z1과 Z2가 서로 상관성이 없도록 결정한다.
- 원래 변수 X의 개수만큼 새로운 변수 Z를 구할 때까지 이 과정을 계속한다.
- 대부분의 변동을 설명하기 위해 필요한 만큼의 주성분을 선택해 남겨놓는다.
- 결과적으로 각 주성분에 대한 가중치 집합을 얻게 된다. 마지막 단계는 원래 데이터를 이 가중치들을 적용해 새로운 주성분으로 변형하는 것이다. 이렇게 얻은 새로운 값들을 예측변수들의 차원이 축소된 형태로 사용할 수 있다.
7.1.3 주성분 해석
1. 주성분에 대한 이해를 돕기 위해 사용되는 표준화된 두 가지 시각화 방법
- 스크리그래프 (주성분의 상대적인 중요도를 표시)
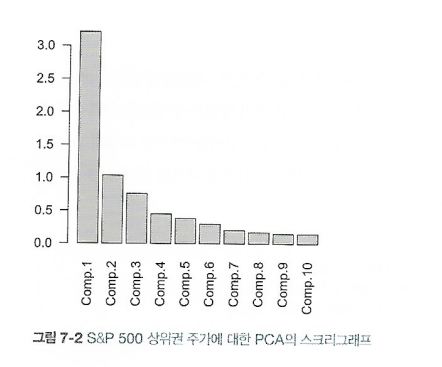
- 상위 주성분들의 가중치 표시
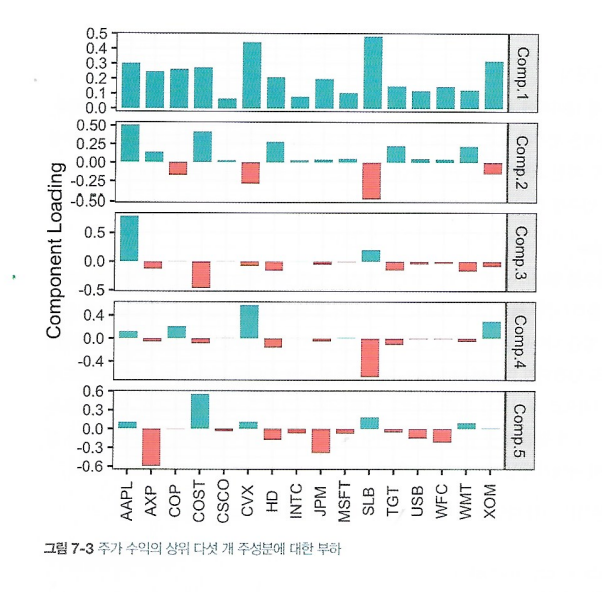
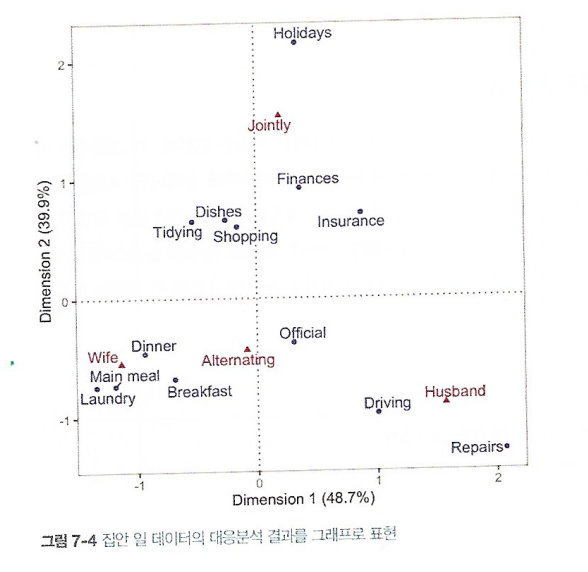
7.1.4 대응분석
- PCA는 범주형 데이터에 사용할 수 없지만, 관련 있는 기술은 대응분석이라고 존재한다.
피터 브루스, 앤드루 브루스의 <데이터 과학을 위한 통계(2판): 데이터 분석에서 머신러닝까지 50가지 핵심 개념> 을 읽고 정리한 내용입니다.