ABSTRACT
이 논문에서는 이전보다 더 깊은 네트워크를 더 쉽게 학습시키기위해 residual learning(잔차학습) framework를 제안하였다.
핵심내용 : 기존의 함수로 학습하기 보다 전의 입력값을 참조하여 학습에 활용하는 것으로 대신한다.
-> ImageNet data set에서 VGGNet 보다 8배 깊은 152개의 layer를 쌓을 수 있었고 더 적은 복잡도를 가진다.
➕ 100개 및 1000개의 레이어로 구성된 CIFAR-10에 대한 분석을 제시
1. INTRODUCTION
네트워크의 깊이가 깊을수록 기능의 수준이 높아진다고 볼수 있지만 training error와 test error 또한 높아짐을 Figuer1.에서 알 수 있다.
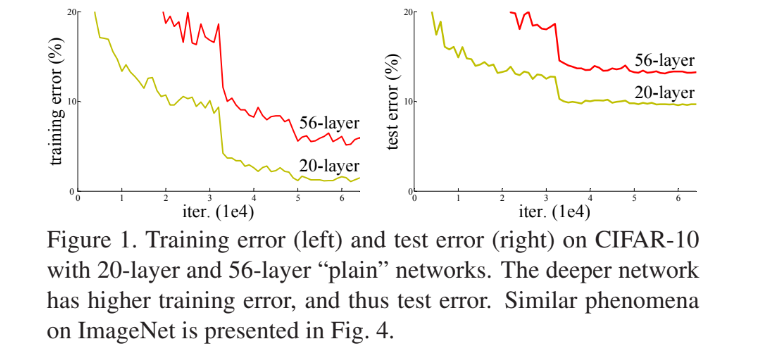
이유는 vanishing/exploding gradients(기울기 소실/폭주)의 문제점이 있기 때문이다.
이러한 문제점은 normalized initial-ization과 intermediate normalization layers를 통해 대부분 해결되었다.
하지만 정확도가 포화되거나 급속도로 감소하는 문제가 발생하였고 (overfitting으로 야기된것이 아님) 이러한 문제점을 해결하기위해 residual learning(잔차학습) framework 를 도입하였다.
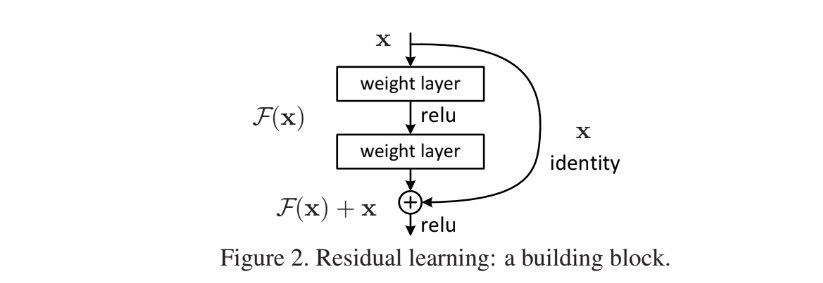
기존 mapping을 H(x)로 나타냈을때 stacked nonlinear layer (쌓여있는 비선형 레이어) 의 mapping인 F(x)는 H(x) - x 를 학습한다는 것이다. 이를 H(x) = F(x) + x 로 재구성할수 있다.
위 그림에서 H(x) = F(x) + x 라는 식이 있을때 학습을 시키며 역전파 방향으로 가면서 미분을 하게되면 F'(x) + 1 이 되므로 F'(x) 가 0에 수렴하게 되더라도 x의 미분값인 1이 더해지기때문에 기울기 소실과 정확도를 잡을수 있다고 이해했다..!
❔ 극단적으로, identity mapping이 최적일 경우, 잔차를 0으로 밀어내는 것이 비선형 레이어의 스택으로 identity mapping을 맞추는 것보다 쉽다는 말이 무슨말인지 잘 이해가 안간다...!
F(x) + x공식은 shortcut connections을 가진 feedforward neural network로 구현할수 있다.
- shortcut(skip) connections : 하나 이상의 layer를 건너뛰는 것
이러한 실험의 결론은 아래와 같다
- 극도로 깊은 잔차학습네트워크는 최적화하기 쉽지만, 잔차학습을 활용하지 않고 단순히 layer를 쌓기만한 일반 네트워크는 깊이가 증가할수록 더 많은 error를 보인다.
- 본 논문의 잔차학습네트워크는 크게 증가한 깊이에서도 정확도 향상을 쉽게 얻을수 있고, 결과도 크게 개선되었다.
2. Related Work
- 잔차 벡터를 이용한 VLAD 및 Fisher Vector는 이미지 검색 및 분류에 강력한 얕은 표현 방법이다.
- 벡터 양자화에서, 잔차 벡터를 인코딩하는 것이 원래 벡터를 인코딩하는 것보다 더 효과적임이 입증되었다.
- Shortcut connections는 오랫동안 연구되어온 이론이다. 초기 MLPs 학습 방법 중 하나는 네트워크 입력에서 출력으로 연결된 선형 레이어를 추가하는 것이다.
- 몇 개의 중간 레이어가 소실(vanishing)되거나 폭주(exploding)하는 gradient problems를 해결하기 위해 보조 분류기에 직접 연결되는 방법도 있습니다.
- Shortcut connections로 구현된 layer esponses, gradients, propagated errors를 중심으로하는 방법도 제안되었다.
- Inception layer는 shortcut branch와 몇 개의 deeper branch로 구성된다.
3. Deep Residual Learning
3.1. Residual Learning
H(x)를 기본매핑이라 했을 때 x는 여러 layer들 중 첫번째 layer의 입력을 나타낸다.\
만약 여러개의 비선형 layer가 있다면 복잡한 함수를 점근적으로 근사시킬수 있고 이는 잔차 함수를 점근적으로 근사할 수 있다는 것과 같다고 할수 있다.
즉, 명시적으로 F(x) := H(x) - x (입력과 출력 차원은 동일) 이라고 할수있으므로 원래 함수는 H(x) := F(x) + x 으로 표현할수 있다.
3.2. Identity Mapping by Shortcuts
잔차학습을 적용하는 방법에는 Identity Shortcut 와 Projection Shortcut이 있고 입력과 출력사이에 shortcut connection을 적용한다.
| Identity Shortcut | Projection Shortcut |
|---|---|
| y = F(x,Wi) + x | y = F(x,Wi) + Wsx |
- x,y : layer의 입출력
- F(x, { Wi} ) : 학습해야할 residual mapping
- Ws : size를 맞춰주는 행렬
Identity Shortcut : 입력과 출력사이의 차원이 같은 경우에 사용\
Projection Shortcut : 입력과 출력사이의 차원이 다를 때 사용
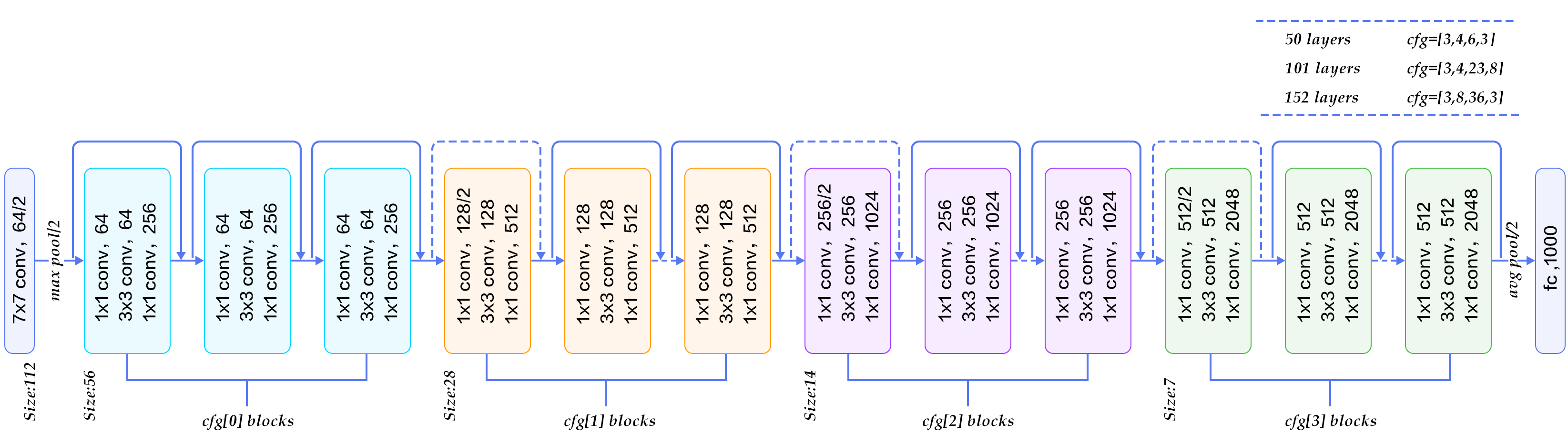
3.3. Network Architectures
Plain Network
- 대부분 3x3 filler 사용
- 동일 출력 feature map 크기에 대해 layer는 동일한 수의 fillter를 가짐.
- feature map 크기가 절반으로 줄어들면 layer 당 시간복잡도를 유지하기 위해 fillter 수가 2배로 증가
- downsampling은 stride =2인 conv layer로 수행
- global average pooling layer 와 a 1000-way fully-connected(FC) layer (with. softmax)로 마무리됨.
- weighted layer는 총 34개
Residual Network.
- Plain Network 와 유사하나 shortcut connection 적용
- 입출력이 동일한 차원인 경우 Identity Shortcut,
- 다른 경우
- Projection Shortcut 적용
- zero entries를 padding하여 Identity mapping 수행
❔ Identity mapping 이랑 Identity shortcut 이 다른것인가..?
3.4. Implementation
- learning rate는 0.1에서 시작, 에러율이 안정화되면 1/10
- 60 x 104 iteration
- weight decay : 0.0001 , momentum : 0.9
- dropout 사용 x
4. Experiments
4.1. ImageNet Classification
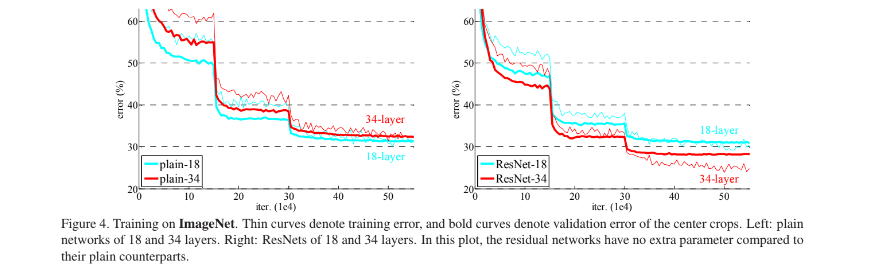
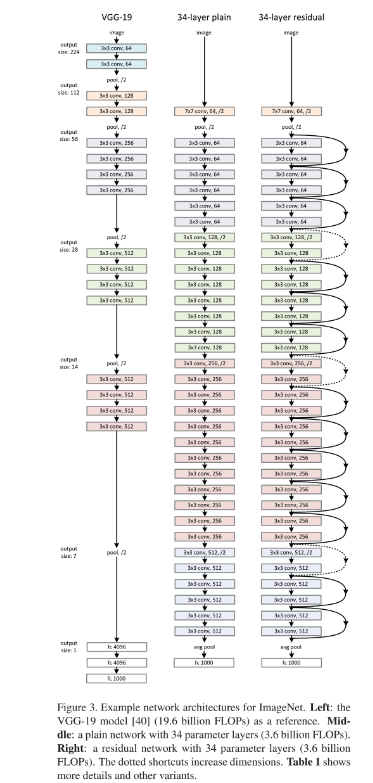
Figure4.는 plain network와 residual network에 대한 error를 나타낸 그림이다.
plain network에서는 layer가 깊어질수록 error가 증가하는 반면 residal network에서는 layer가 깊어져도 낮은 error를 보이는 것을 확인할수 있다.
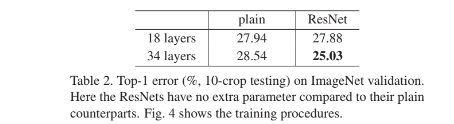
Table2.는 학습된 18-layer,34-layer plain/residual network의 validation data에 대한 10-crop testing 결과중 Top-1 error를 보여주고 있고 34-layer esidual network의 error가 가장 낮은것을 확인할 수 있다.
Deeper Bottleneck Architectures.
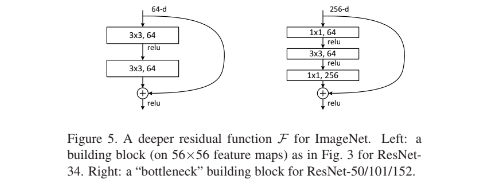
각 잔차함수 F에 대해 3개의 layer stack을 사용하는데 1x1 layer로 차원을 줄이고 3x3 conv . 수행후 1x1로 차원을 늘려 원하는 채널을 맞추어 준다. 이러한 방식으로 bottleneck을 사용하면 모델을 깊게 쌓으면서 더 많은 학습을 가능하게 한다.