OpenAI GYM - CartPole with Q-Learning

MinSeok_CSE·2025년 2월 11일

OpenAi Gym

목록 보기

1/2

🎓 CartPole 실험 개요

본 실험은 OpenAI Gym의 CartPole-v1 환경에서 Q-learning을 적용하여 강화 학습을 진행한 실험이다.
일반적으로 CartPole 문제는 DQN(Deep Q-Network)을 이용하여 해결하는 경우가 많지만, 이번 실험에서는 저번에 공부한 Q-learning을 활용하여 학습 과정과 성능을 직접 확인하는 것을 목표로 하였다.

특히, 행동 선택 방식(Exploration Strategy)에 따른 학습 성능 차이가 궁금하여 각 방식에 대한 실험도 진행하였다.

첫 번째 방식은 Epsilon-Greedy(ε-그리디) 탐색법이며, 두 번째 방식은 Softmax Policy 기반 행동 선택이다.

추가적으로 Epsilon-Greedy 방식에서는 가우시안 노이즈(Gaussian Noise)를 적용하여 행동 선택의 다양성을 증가시켰다.

본 실험을 통해 각 행동 선택 방식이 학습 성능에 미치는 영향을 비교 분석하고, 어떤 방식이 CartPole 환경에서 더 효과적인 학습을 유도하는지 확인하는 것이 목적이다. 참고로 이 글에서는 실험에 진행한 코드가 등장하지 않고 결과적인 부분과 어떤식으로 코드를 구성하였는지만 나오는 글이다.

🎓 OpenAI Gym이란?

OpenAI Gym은 OpenAI에서 개발한 강화 학습 환경 라이브러리로, 다양한 RL 알고리즘을 연구하고 실험할 수 있도록 설계되었다. 이후 OpenAI가 Gym을 직접 관리하지 않기로 결정하면서, Gymnasium이 후속 프로젝트로 개발되었다. Gymnasium은 Farama Foundation에서 유지보수를 담당하며, OpenAI Gym과 완벽한 하위 호환성을 유지하면서도 더욱 안정적이고 확장 가능한 기능을 추가하였다.

🎓 CartPole 소개

CartPole은 고전 제어(Classic Control) 문제 중 하나로, 강화 학습(Reinforcement Learning, RL)에서 널리 사용되는 환경이다. 이 환경은 역진자(Inverted Pendulum) 문제를 기반으로 하며, 막대(Pole)가 수직으로 서 있도록 균형을 유지하는 것이 목표이다.

🛠 실습 환경

사용한 환경 : Anaconda, PyCharm
강화 학습 환경 : OpenAI Gym
파이썬 버전 : 3.8

📝 CartPole 환경 정보 및 설명

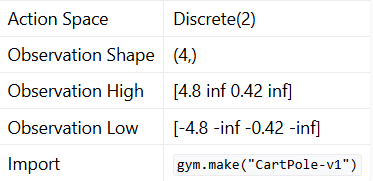
위 데이터는 OpenAi Gym에서 제공하는 가상의 물리적인 값으로 생각하면 된다. 앞으로 다양한 실습을 하기 위해서 위에서 설명하는 각 요소가 어떤 역할인지 잘 알아두면 좋다.

Action Space Discrete(2) (좌/우 이동)
- Discrete(2): 이산 공간(Discrete) 형태이며, 두 개의 선택지만 존재함.
  - 가능한 행동:
    - 0: 수레(Cart)를 왼쪽으로 이동
    - 1: 수레(Cart)를 오른쪽으로 이동
- 예시:
  - 에이전트가 0을 선택하면 수레가 왼쪽으로 이동함.
  - 에이전트가 1을 선택하면 수레가 오른쪽으로 이동함.
Observation Shape (4,) (4개의 상태 변수)
- (4,): 관측 공간(Observation Space)의 형태를 나타냄.
  - 총 4개의 상태(State) 변수를 포함
  - 각각 수레와 막대의 위치 및 속도를 나타냄
- 예시:
  - 환경에서 반환하는 카트의 물리적인 관측 값: [0.2, -0.5, 0.1, 0.02]
Observation High [4.8, ∞, 0.42, ∞] (상태 변수의 최댓값)
- 관측 공간에서 각 상태 변수의 최대 허용값을 나타냄
  - 4.8: 수레 위치(Cart Position)의 최댓값 (경계를 넘으면 종료)
  - ∞: 수레 속도(Cart Velocity)의 최댓값 (이론적으로 제한 없음)
  - 0.42: 막대 각도(Pole Angle)의 최댓값 (약 24도 이상 기울어지면 종료)
  - ∞: 막대 각속도(Pole Angular Velocity)의 최댓값 (이론적으로 제한 없음)

Observation Low [-4.8, -∞, -0.42, -∞] (상태 변수의 최솟값)
- 관측 공간에서 각 상태 변수의 최소 허용값을 나타냄
  - -4.8: 수레 위치(Cart Position)의 최솟값 (경계를 넘으면 종료)
  - -∞: 수레 속도(Cart Velocity)의 최솟값 (이론적으로 제한 없음)
  - -0.42: 막대 각도(Pole Angle)의 최솟값 (약 -24도 이하 기울어지면 종료)
  - -∞: 막대 각속도(Pole Angular Velocity)의 최솟값 (이론적으로 제한 없음)
Import gym.make("CartPole-v1") (환경 생성)
- CartPole 환경을 생성하는 코드
- OpenAI Gym/Gymnasium에서 CartPole 환경을 실행할 때 사용

CartPole 환경 설명

물리적 구조 및 목표
- 수레 위에 회전 가능한 막대가 부착된 형태
- 목표: 막대가 넘어지지 않도록 최대한 오래 유지
상태(State)와 행동(Action) 정의
- 상태: Cart 위치, Cart 속도, 막대 각도, 막대 각속도 (총 4가지)
- 행동:
  - 0: 왼쪽으로 힘을 가함
  - 1: 오른쪽으로 힘을 가함
보상(Reward) 및 에피소드 종료 조건
- env.step(action)을 수행하면 환경에서 기본적으로 제공하는 보상(reward)을 받음.
- 보상 시스템
  - 각 타임스텝마다 +1 보상이 부여됨.
  - 즉, 막대를 오래 유지할수록 총 누적 보상이 커짐.
- 에피소드 종료 조건 (Penalty 적용 상황)
  - 막대가 ±12도 이상 기울어지면 즉시 종료
  - 수레가 ±4.8 위치를 초과하면 즉시 종료
- 추가 패널티 적용
  - 200 스텝을 채우지 못하고 종료되면 추가적인 패널티를 적용.
  - 패널티 크기: reward = min(-(200 - cnt), -50) (최소 -50으로 제한).
  - 즉, 빨리 종료될수록 더 큰 패널티를 받음.
  - 패널티 크기는 임의로 결정한 것이니 본인의 생각대로 수정하는 것이 좋다.

랜덤 에이전트 실험

Gym을 이용한 환경 불러오기 환경 초기화 및 기본 동작 확인

랜덤 에이전트(Random Agent)는 강화 학습 없이 무작위 행동(Random Action)을 수행하는 에이전트임.
즉, 환경의 상태를 고려하지 않고 무작위로 행동을 선택하며, 이를 통해 환경의 기본 동작을 확인할 수 있음.
실험 목적
- 강화 학습을 적용하기 전에 기본적인 환경 동작과 보상 체계를 확인하는 단계.
- 랜덤 에이전트의 성능을 측정하여, 학습된 에이전트와 비교하는 기준을 설정.
실험 결과
- 랜덤 에이전트는 막대의 균형을 유지하지 못하고 빠르게 종료됨.

강화 학습 알고리즘 적용

강화 학습을 적용하여 에이전트가 학습하도록 함.
이 코드에서는 Q-learning 알고리즘을 사용하여 CartPole 환경에서 학습을 진행함. 보통 CartPole 문제는 DQN 알고리즘을 사용하여 구현하는 문제이다. 하지만 이번에는 Q-Learning의 공부를 확인하고 싶어 Q-Learning를 사용하여 CartPole의 문제를 해결하였다.
Q-table을 CartPole 환경을 기반으로 생성
- Q-table은 CartPole의 상태 공간(Observation Space)과 행동 공간(Action Space)을 바탕으로 구성되었다.
- CartPole의 환경 정보는 다음과 같다
- 위 정보를 바탕으로 Q-table을 구성
- Action Space → Discrete(2): 두 가지 행동 (0: 왼쪽, 1: 오른쪽)
- Observation Space → 4개의 상태 변수를 각각 20개 구간(bin)으로 이산화(Discretization)
- 따라서, Q-table의 크기는 (20, 20, 20, 20, 2) = 320,000개 상태-행동 쌍
  - bin 값이 많을수록 Q-table이 더욱 상세해져 학습이 잘 진행되는 것을 확인했다.
  - 하지만 bin 개수가 커질수록 메모리 사용량이 매우 증가하고 학습 시간이 길어지는 문제가 발생하였다.
  - 내 컴퓨터 성능을 고려했을 때, bin = 20이 한계였다.
주요 학습 과정
1. 환경 초기화 (env.reset())
2. 현재 상태를 이산(discretized) 상태로 변환
3. 탐색률(Exploration Rate)에 따라 행동 선택
  - 확률적으로 무작위 행동(탐색) 또는 최적 행동(활용) 수행
4. 행동 실행 후 보상과 새로운 상태 확인
5. Q-테이블 업데이트
  - Q(s, a) = (1 - α) * Q(s, a) + α * (reward + γ * max Q(s', a'))
6. 종료 조건이 충족될 때까지 반복
학습 목표
- 최적의 정책을 학습하여 막대를 최대한 오래 유지하는 것.
- 랜덤 에이전트보다 더 높은 보상을 얻을 수 있도록 행동을 최적화함.
- 600 스텝 이상 유지할 수 있도록 목표를 결정하였다.

행동 선택 방식 실험 (Softmax & Epsilon-Greedy)

강화 학습에서 행동을 선택하는 방법을 비교 실험함.
두 가지 방식으로 행동을 선택하여 탐색(Exploration)과 활용(Exploitation)의 균형을 조절함.

1️⃣ Epsilon-Greedy (ε-그리디) 탐색법

확률 ε에 따라 탐색(랜덤 행동 선택)과 활용(최적 행동 선택)을 결정하는 방식.
ε은 학습이 진행될수록 감소하도록 설정하여 초반에는 탐색을 많이 하고 후반에는 최적 정책을 따르게 함.
CartPole에서 많이 사용하는 행동 선택 방식이다.

2️⃣ Softmax Policy 기반 행동 선택

Q값이 높은 행동을 확률적으로 더 자주 선택하는 방식.
softmax() 함수를 사용하여 모든 행동의 선택 확률을 부드럽게 조절함.

📊 결과 및 분석

🔹 Q-table 이산화 수준(Binning)에 따른 학습 성능 변화

처음에는 bin 값을 5로 설정하여 학습을 진행했으나, Q-table이 너무 거칠어져 학습이 제대로 이루어지지 않았다.

CartPole 환경에서 연속적인 상태를 이산화(Discretization)하여 학습하는 방식이기 때문에, bin 개수가 작을수록 Q-table의 해상도가 낮아지고 학습 성능이 저하되는 현상이 발생하였다.

이후 bin 값을 점차 증가시키면서 실험을 진행하였으며, Q-table이 세밀해질수록 학습 성능이 향상된다는 것을 확인할 수 있었다. 하지만 bin 값이 너무 커지면 메모리 사용량과 학습 시간이 급격히 증가하는 문제가 발생하였으며, 결과적으로 bin=20이 적절한 균형을 유지할 수 있는 최적의 값이었다.

🔹 행동 선택 방식 비교 (Epsilon-Greedy vs Softmax)

이번 실험에서는 행동 선택 방식에 따른 학습 성능 비교를 진행하였다.

두 가지 방식(Epsilon-Greedy, Softmax)을 적용하여 학습을 수행하고, 각 방식의 학습 성능 및 수렴 속도를 비교하였다.

✅ Epsilon-Greedy 방식

탐색률(ε)을 점진적으로 감소시키면서 최적 행동을 찾아가는 방식으로 학습이 진행됨.
학습이 진행될수록 탐색(Exploration)을 줄이고 최적 행동(Exploitation)을 강화하여 안정적인 정책을 형성함.
결과적으로 Softmax 방식보다 더 빠르게 학습이 진행되었으며, 최종적으로 더 높은 성능을 기록하였다.

✅ Softmax 방식

Q값을 확률 분포로 변환하여 행동을 선택하는 방식으로 학습이 진행됨.
특정 행동이 절대적으로 선택되지 않고, 학습 과정 내내 일정한 확률로 모든 행동이 선택될 가능성이 존재함.
Epsilon-Greedy 방식에 비해 최적 행동으로 빠르게 수렴하는 속도가 다소 느렸으며, 최종 성능도 낮았다. 즉 한계가 명확했다.

📌 결론:
결과적으로 모든 방식에서 학습이 원활하게 진행되었으며, CartPole의 목표를 성공적으로 달성할 수 있었다.

그중에서도 Epsilon-Greedy 방식이 학습 속도와 최종 성능 측면에서 더 우수한 결과를 보였다.

반면, Softmax 방식은 탐색이 지속적으로 이루어지지만, 일정 한계를 넘어서면 새로운 탐색을 시도하는 빈도가 줄어드는 경향이 나타났다. 즉, Softmax 방식은 현재의 최적 정책을 유지하려는 성향이 강해져, 더 높은 보상을 얻기 위한 도전이 제한되는 모습을 보였다.

반대로, Epsilon-Greedy 방식은 학습이 진행되면서도 지속적인 탐색을 수행하며, 더 나은 보상을 찾기 위해 시도하는 빈도가 높았다. 이러한 특성 덕분에 Epsilon-Greedy 방식이 보다 유연한 학습을 가능하게 하였으며, 최적 정책을 찾는 데 있어 더 효과적인 결과를 보였다.

위 영상은 Epsilon-Greedy 방식의 영상이다.

🔹 Epsilon-Greedy에서 가우시안 노이즈 적용 실험

추가적으로 Epsilon-Greedy 방식에서 Q값에 가우시안 노이즈(Gaussian Noise)를 추가하는 실험을 진행하였다. 가우시안 노이즈를 적용하면 비슷한 Q값을 가진 행동 간에 선택 확률이 조금씩 변할 수 있도록 조정하는 역할을 한다.

하지만 실험 결과, 일반적인 Epsilon-Greedy 방식과 성능 차이가 없다 싶을 정도로 달라지지 않았다.

즉, 가우시안 노이즈를 추가한다고 학습이 크게 달라지지는 않았으며, Epsilon-Greedy만으로도 충분한 학습 성능을 확보할 수 있었다.

📈 WandB 그래프 비교 (Epsilon-Greedy vs Softmax)

아래 그래프는 Epsilon-Greedy 방식과 Softmax 방식의 학습 진행 과정을 비교한 그래프로 각 방식에서 가장 학습이 잘 진행된 그래프들을 비교한 것이다.

각 실험에서 최소 보상(Min Reward), 최대 보상(Max Reward), 평균 보상(Average Reward)을 기록하여 학습 성능을 비교하였다. 그래프에서 파란색 선이 Epsilon-Greedy 방식, 주황색 선이 Softmax 방식을 나타낸다.

보상(Reward)은 막대가 쓰러지지 않고 오래 버틸수록 더 많이 획득되므로,
그래프에서 보상이 높을수록 더 오래 살아남아 CartPole의 목표를 성공적으로 달성한 것을 의미한다.

즉, 그래프의 보상이 높게 형성될수록 해당 방식이 더 효과적으로 학습되었음을 나타낸다.

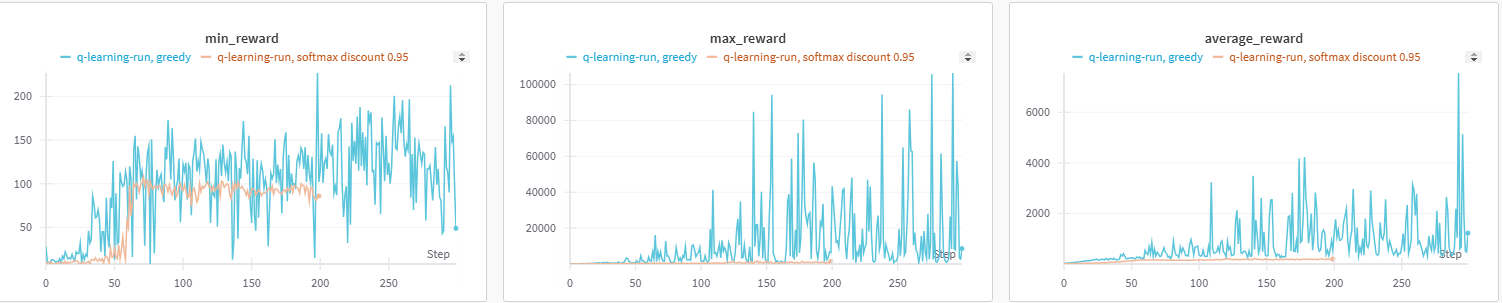
Epsilon-Greedy 방식은 무려 10분 이상을 버티며 Reward를 획득하여 100,000 이상을 얻은 결과도 있다.

🎓 마무리 및 추가 실험 가능성

이번 실험에서는 Q-learning을 적용하여 CartPole 환경에서의 학습 성능을 분석하였다.
Epsilon-Greedy 방식과 Softmax 방식을 비교한 결과, Epsilon-Greedy 방식이 더 효과적으로 학습되었으며,
탐색과 활용의 균형을 유지하면서도 더 높은 보상을 기록하는 경향을 보였다.

하지만 일반적으로 CartPole 문제는 DQN(Deep Q-Network)을 활용하여 해결하는 경우가 많다. 따라서, 앞으로는 DQN을 사용한 CartPole 학습을 진행하여 성능을 비교할 예정이다. DQN을 활용하면 신경망을 통해 연속적인 상태 공간을 직접 처리할 수 있어, Q-table을 사용하는 Q-learning보다 더 확장성이 높은 방식을 실험할 수 있을 것으로 기대된다.

또한, CartPole을 포함하여 클래식 컨트롤(Classic Control) 문제 5가지에 도전할 예정이다.

OpenAI Gym의 대표적인 클래식 컨트롤 환경은 다음과 같다.

CartPole-v1 (현재 실험 진행 완료)
Acrobot-v1
MountainCar-v0
Pendulum-v1
LunarLander-v2

[참고] https://www.gymlibrary.dev/environments/classic_control/

MinSeok_CSE

다음 포스트