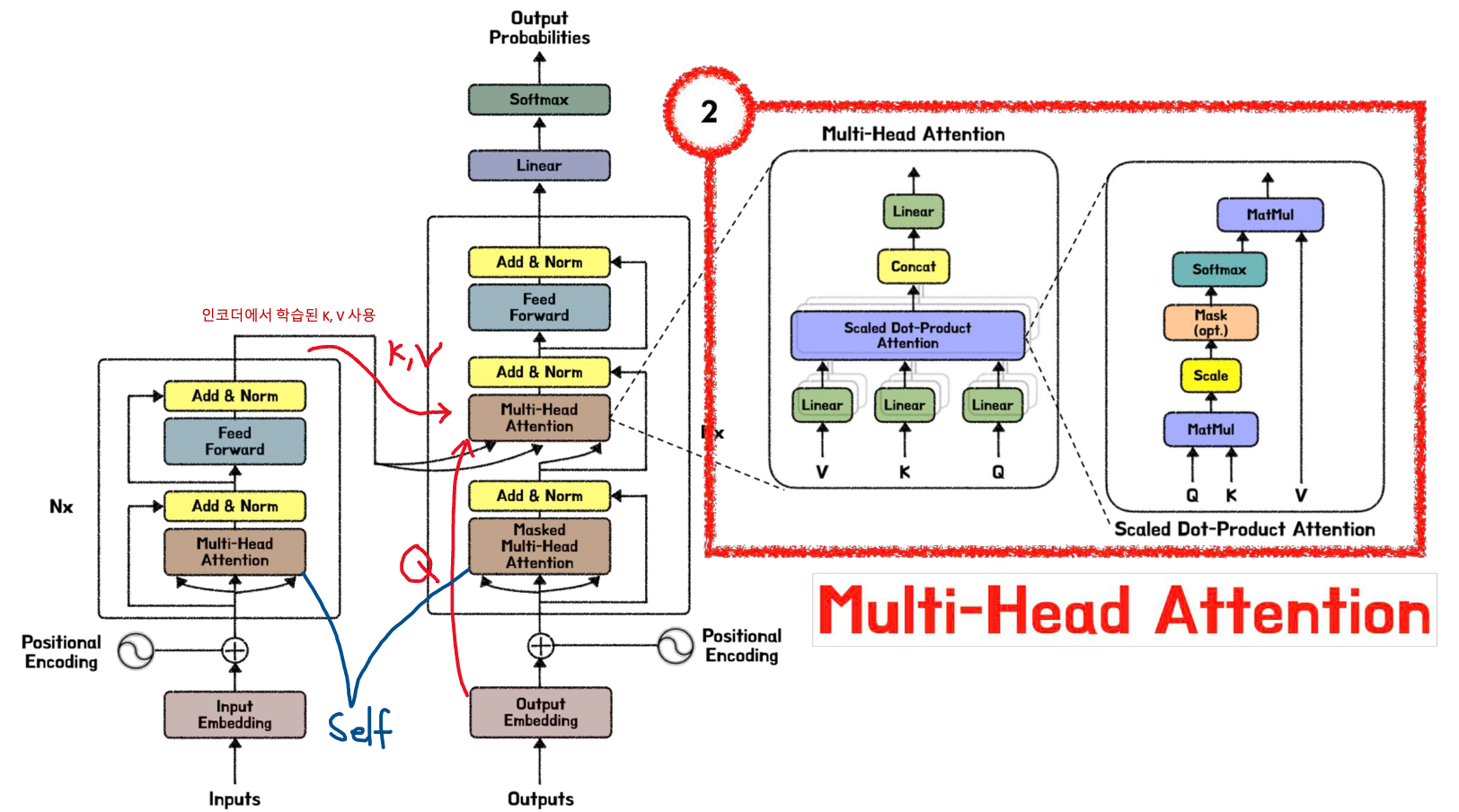
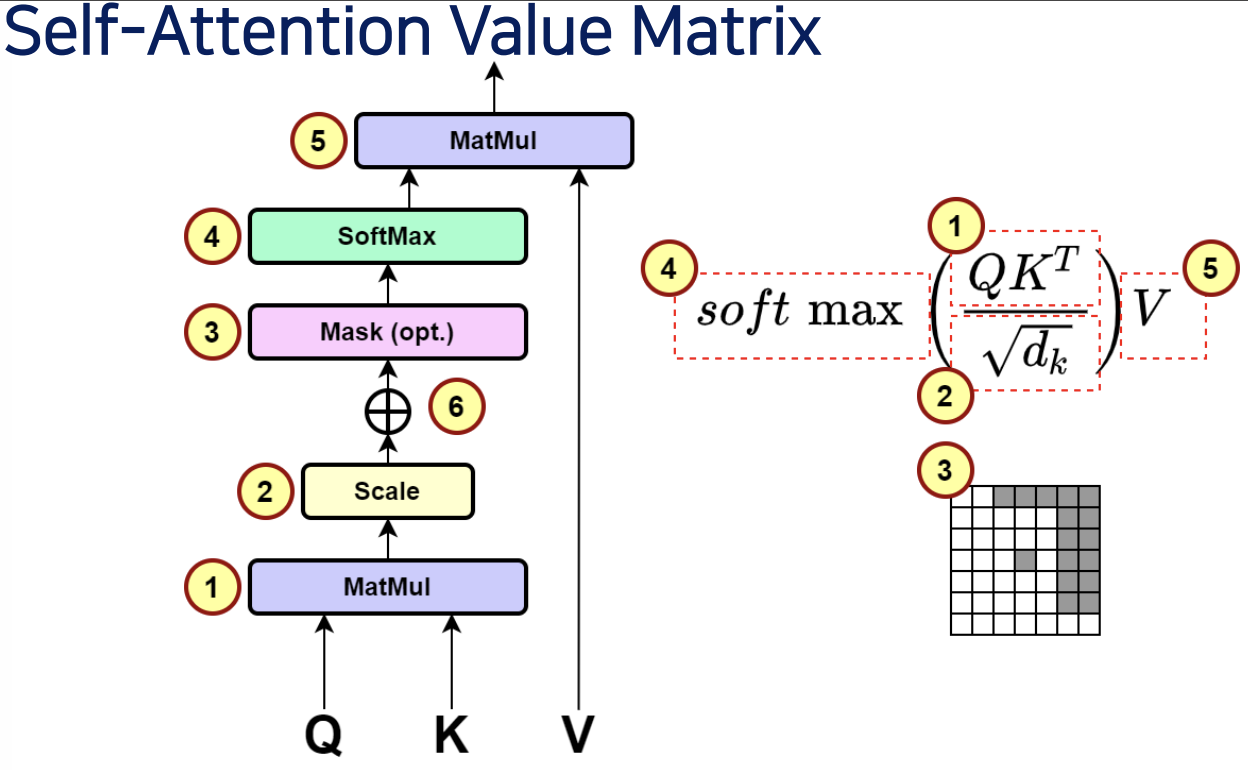
하나의 레이어 안에 Scaled Dot-Product attention (attention value matrix) 를 구하는 것 뿐만 아니라, 필수적으로 필요한 Sub-Layer 가 있다.

CH5

Scaled-Dot Product Matrix 리뷰 & 핵심

• Attention Value(최종 결과값) : $attenton(Q, K, V)$
• Attention Score : $QK^T$

Matrix Dimension of One Head

• 멀티 헤드가 아닌 One 헤드만 사용하는 경우
• One Head of Self Attention = One Self Attention Value Matrix:
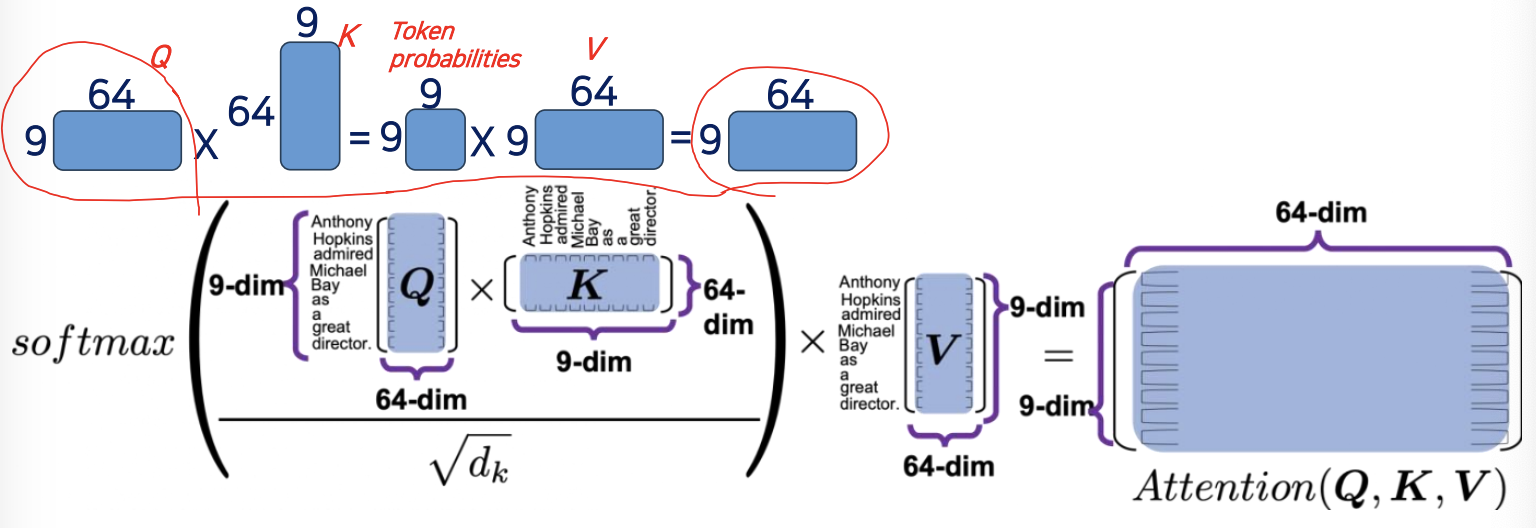
  • $Q(9 \times 64) \times K(64 \times 9) \times V(9 \times 64) \to 9 \times 64$ Matrix

Input Word Embedding (Tokenization)

• Input (Word) Embedding
  • Input에 입력되는 데이터(Sentence 안의 단어들)를 소프트웨어(컴퓨터) 가 이해할 수 있도록 Matrix(행렬) 값으로 바꾸어 주는 과정
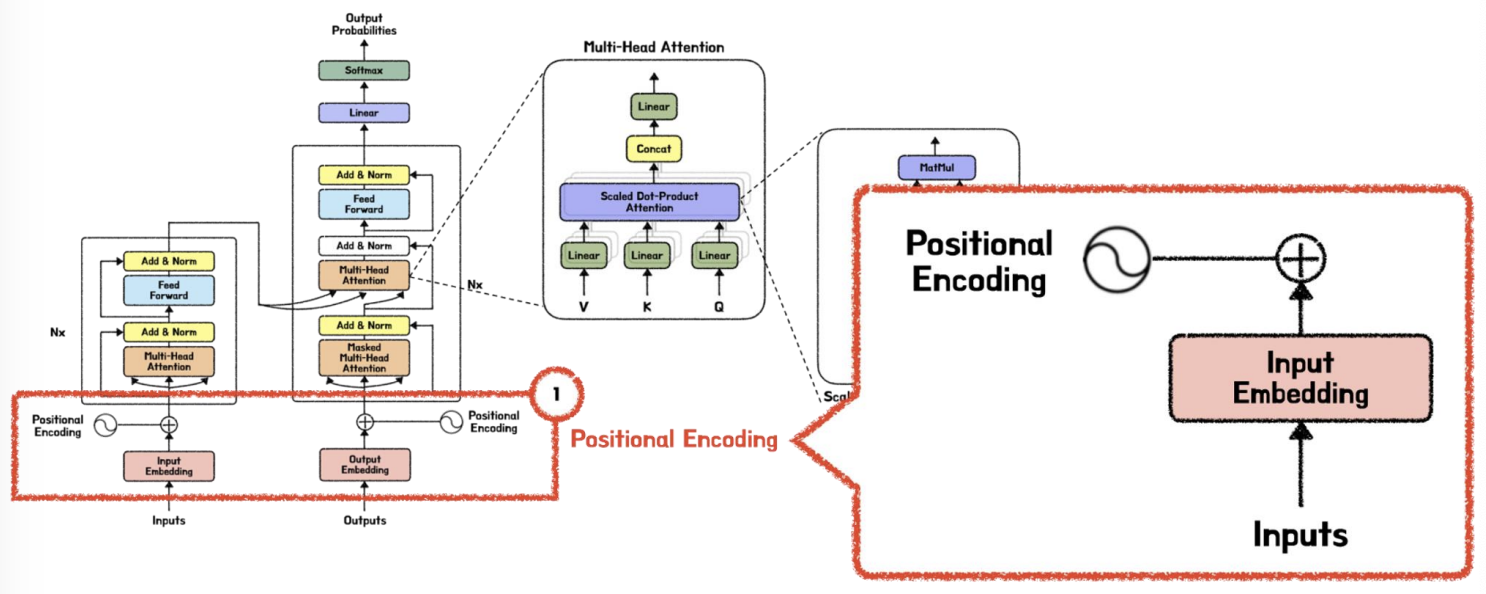
  • Input Embedding + Positional Encoding 해줘야 한다.
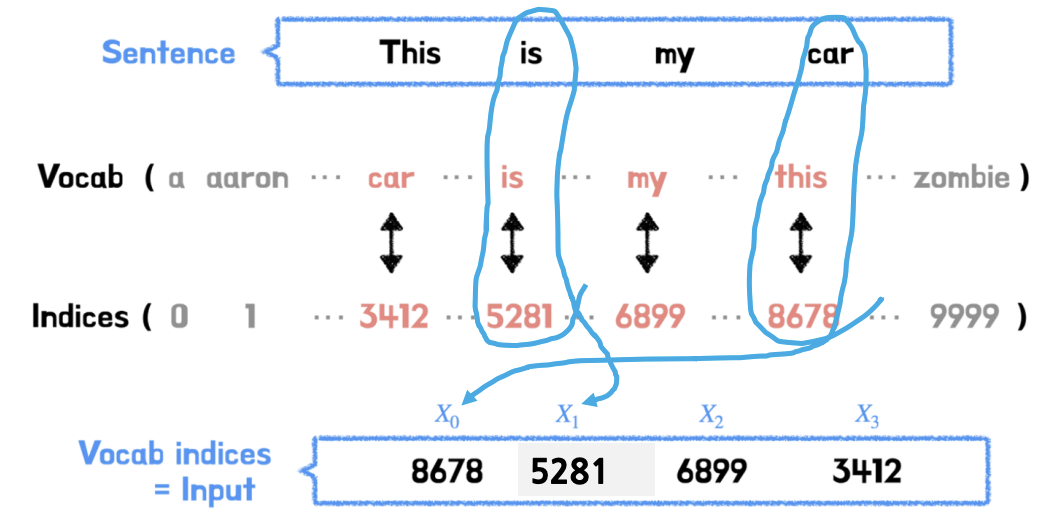
  • 트랜스포머와 GPT는 각자 자신만의 Vocabulary-Index Matching Table(DB) 가 있다. 우리는 아래와 같이 입력 문장 어휘(단어)에 일치하는 모든 인덱스(indices)를 검색합니다
  • Example
    • This 에 대한 인덱스 번호를 $3412$ 로 하겠다. is 에 대한 인덱스 번호를 $5281$ 로 하겠다...
    • 그러한 인덱스 번호를 $X_0, X_1, ... , X_3$ 로 표현하기도 한다.
    • 아래와 같이 문장이 순서대로 들어오는 것이 아니라, $8678$ 에 해당하는 car 부터 오고 순서가 맞지 않는다.
• Vector of Feature(=Input Word)
  • 각 단어 (vocabulary) 인덱스는 유니크한 벡터 (한 단어마다 임베딩 벡터의 64 차원까지 표시하지고 약속을 했다) 를 가진다.
  • 그러나 단순화를 위해 우리는 아래와 같이 4차원의 고유 임베딩 벡터를 가정힌다(실제로는 4개의 차원이 아님)
  • 계속 해서 학습 하다 보먄 this 의 weight 값들이 바뀌게 된다 (즉 this 라는 것이 car 에 가까워 진다)
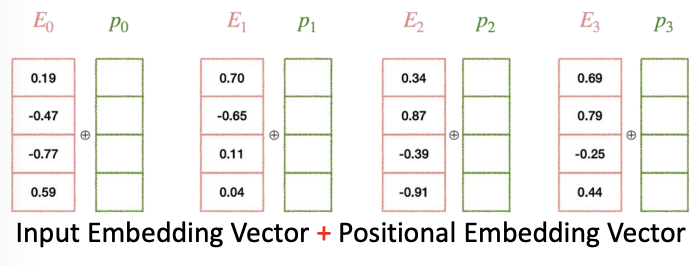
  • 임베딩 벡터 $E_0, E_1, E_2, E_3$가 포지셔널 임베딩 벡터에 추가됩니다

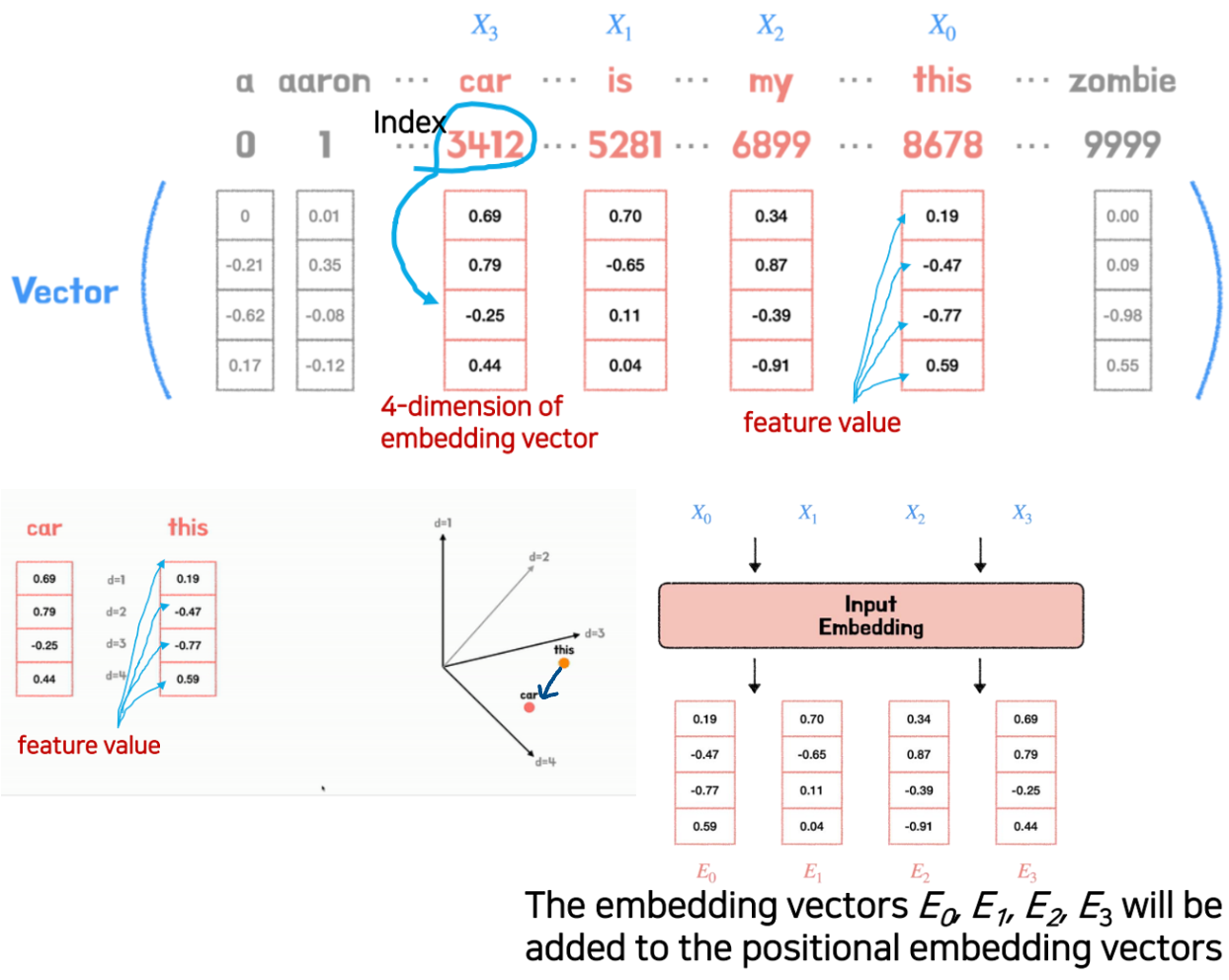
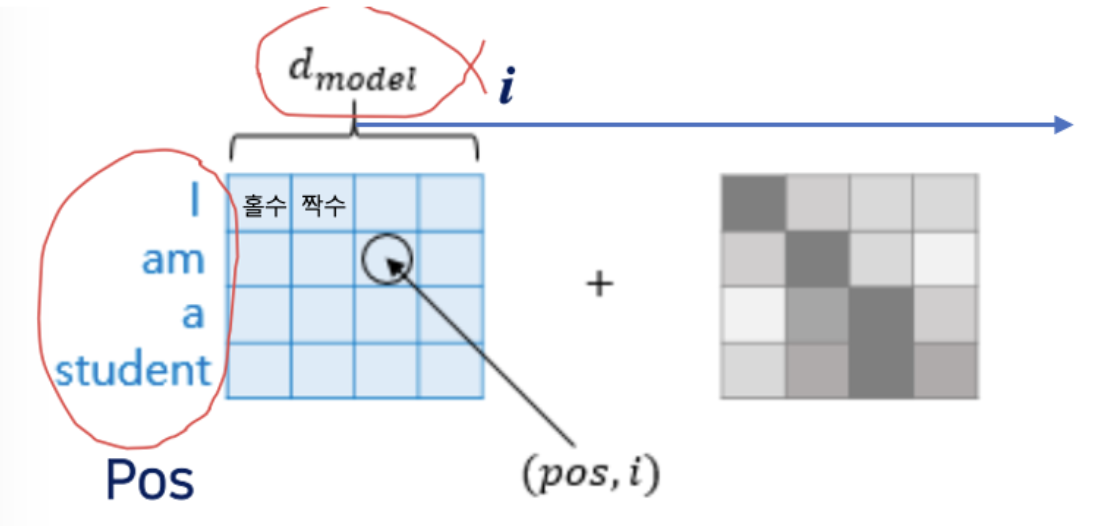
Input Embedding Vector + Positional Embedding Vector

• 트랜스포머에서는 단어의 위치를 순차적으로 처리할 수 없기 때문에, 반드시 그 단어가 문장에서 몇번쨰에 위치했던 것 인지를 설정해주는 Positional Embedding 이 합쳐져야한다. 그래야 구분이 된다.
• 입력 임베딩 벡터(word)를 Positional Embedding Vector 에 추가하여 문장 내 단어의 위치를 식별합니다.
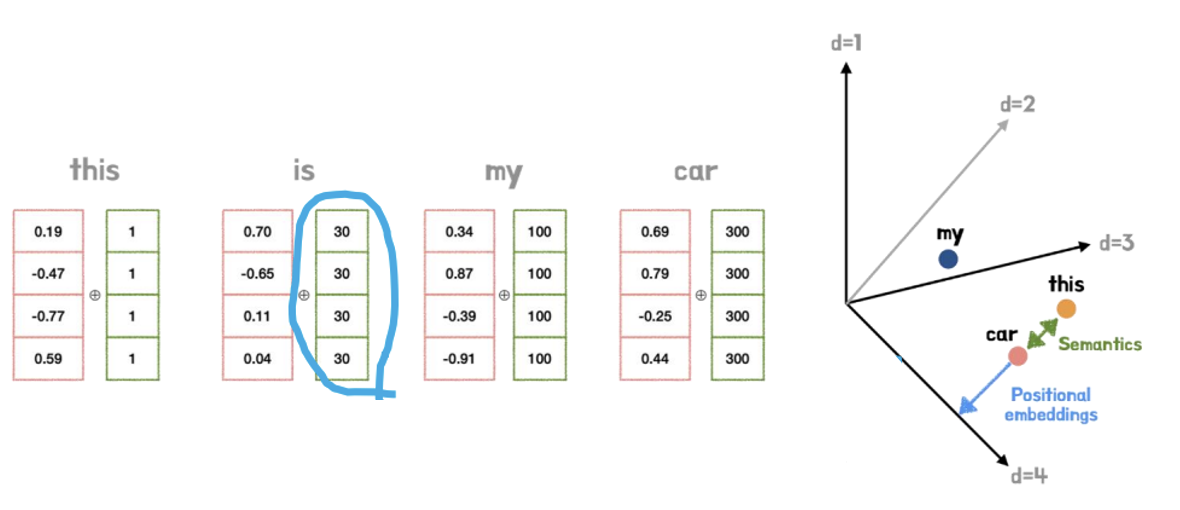
• 단어들의 순서가 바뀌더라도, 문장 내 각 단어의 위치는 Positional Embedding Vector 에 의해 식별될 수 있습니다

❶ Although I did no get 95 in last TOEFL. I could get in the Ph.D programs.
❷ Although I did get 95 in last TOEFL. I could not get in the Ph.D programs.

문장 내의 'not'의 위치 차이로 두 문장의 뜻이 완전히달라져 버렸음. 따라서 문장 내에서 단어 위치를 알려주는 Positional Embedding Vector 는 매우 중요

만약 아래의 예제처럼 Positional Embedding Vector 의 Feature Value 들이 Input Embedding Vector 의 Feature Value 들에 비해 상대적으로 너무 커버리면 단어간 Similarity 값들이 너무 작아지게 되어서 Attention Layer 에서 제대로 학습이 되지 않기 때문에 Input Embedding 값들보다 상대적으로 훨씬 작아야 함.

---

Fully-connected Feedforward Neural Network (FFNN)

• backpropagation 이 없다.
• 그냥 일반적인 RNN 이라고 하면 역전파가 들어가있는데, 트랜스포머에서 사용하는 RNN 은 역전파가 없는 Feedforward 만 사용한다.
• 그래서 마지막 output 에서는 소프트맥스에 의해서 output probabilites 확률이 나온다.

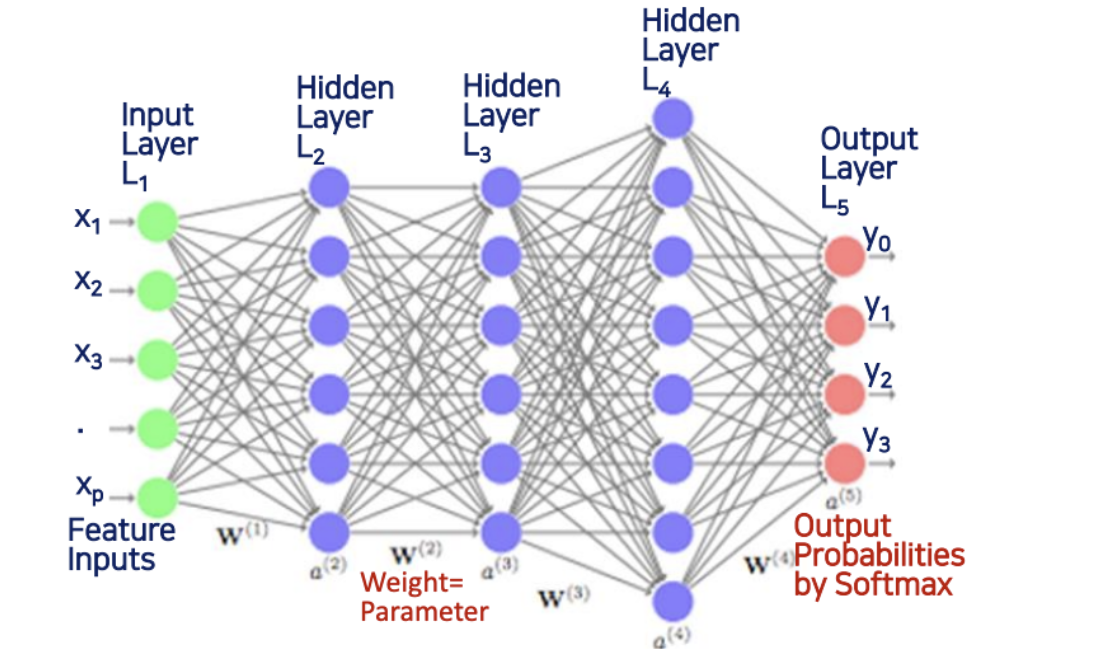
Position-Wise FFNN

Fully-connected Feedforward Neural Network (FFNN or FF)

• 인코더와 디코더 모두 끝 부분에 FFNN이 있습니다
• FF에는 Softmax, ReLu, Leaky ReLu, Hyperbolic, 등의 활성화 함수가 있습니다,
• FFNN은 인코더 또는 디코더의 하위 계층 중 하나로 사용되며, 확률을 계산하려면 Decoder가 필요합니다
  • 인코더는 입력 시퀀스를 처리하고 인코딩된 정보를 제공하지만 확률을 계산하지 않습니다. 확률적 예측 및 출력 시퀀스 생성은 주로 디코더의 역할입니다
• FFNN은 각 토큰(각 위치)에 적용되므로 'Position-Wise'라고 불립니다
• FFNN 도 역시 마찬가지로 weight 을 업데이트하는 과정을 거친다.
• FFNN 을 거쳐서 토큰마다 독립적인 output 을 산출

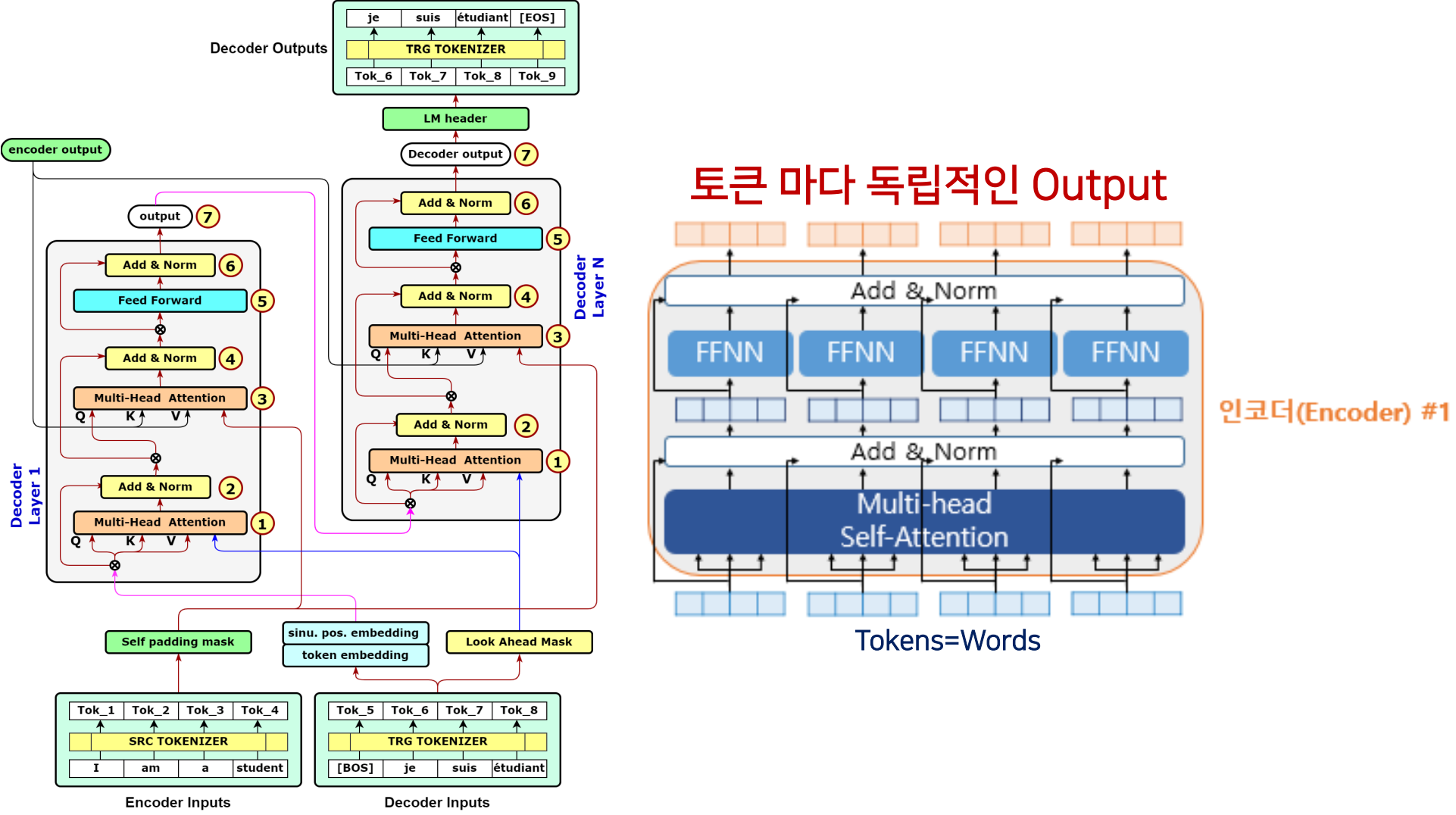
Key Hyperparameters

2017년 12월 4일부터 7일까지 미국 캘리포니아주 Long Beach에서 제31회 신경 정보 처리 시스템 컨퍼런스(NIPS 2017)에 발표된 "Attention Is All You Need" 논문에서 제안된 주요 하이퍼 파라미터 수

• seq_len = 문장의 토큰 수 (size) (vector)
• d$_{model}$ = 512
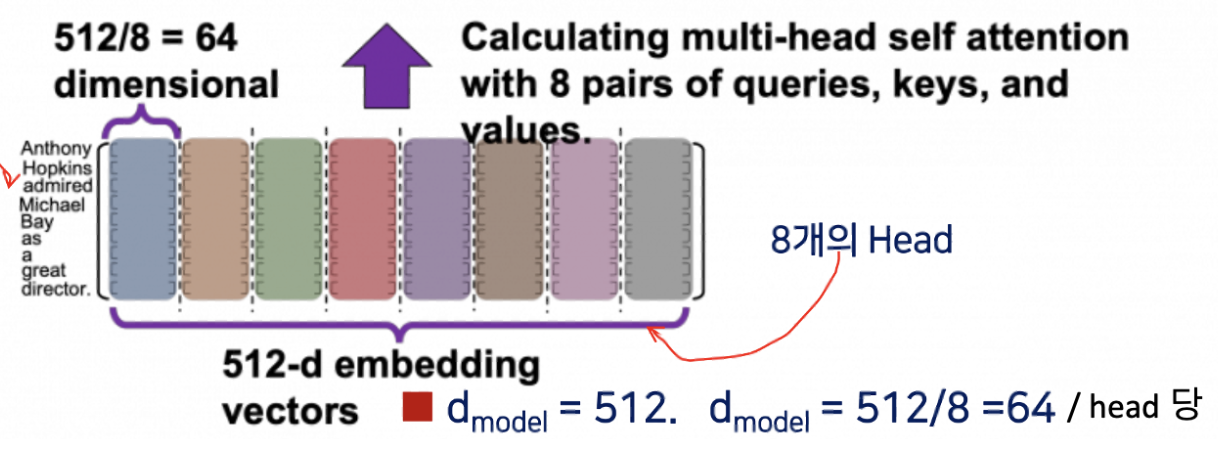
  • 한 단어의 컬럼은 64 라고 했었다. 그런데 왜 512일까?
  • head 의 개수가 8개라고 했는데
  • 8개의 멀티 헤드가 동시에 Encoder Input 에서 입력이 되면 모두 512 개가 되는 것이다.
  • 8 heads $\times$ 64 dimension (헤드 하나당 토큰이 차지하는 컬럼이 64개)
• num_layers = 6 (번을 반복하겠다)
• num_heads = 8
• d$_{ff}$ = 2048 (# of nodes of FFNN hidden layer, dimension of feadforward 약자)
  $\therefore$ Size of FFNN Input = Size of FFNN Output = d$_{model}$ = 512

하이퍼파라미터들은 얼마든지 다르게 설정할 수 있다.

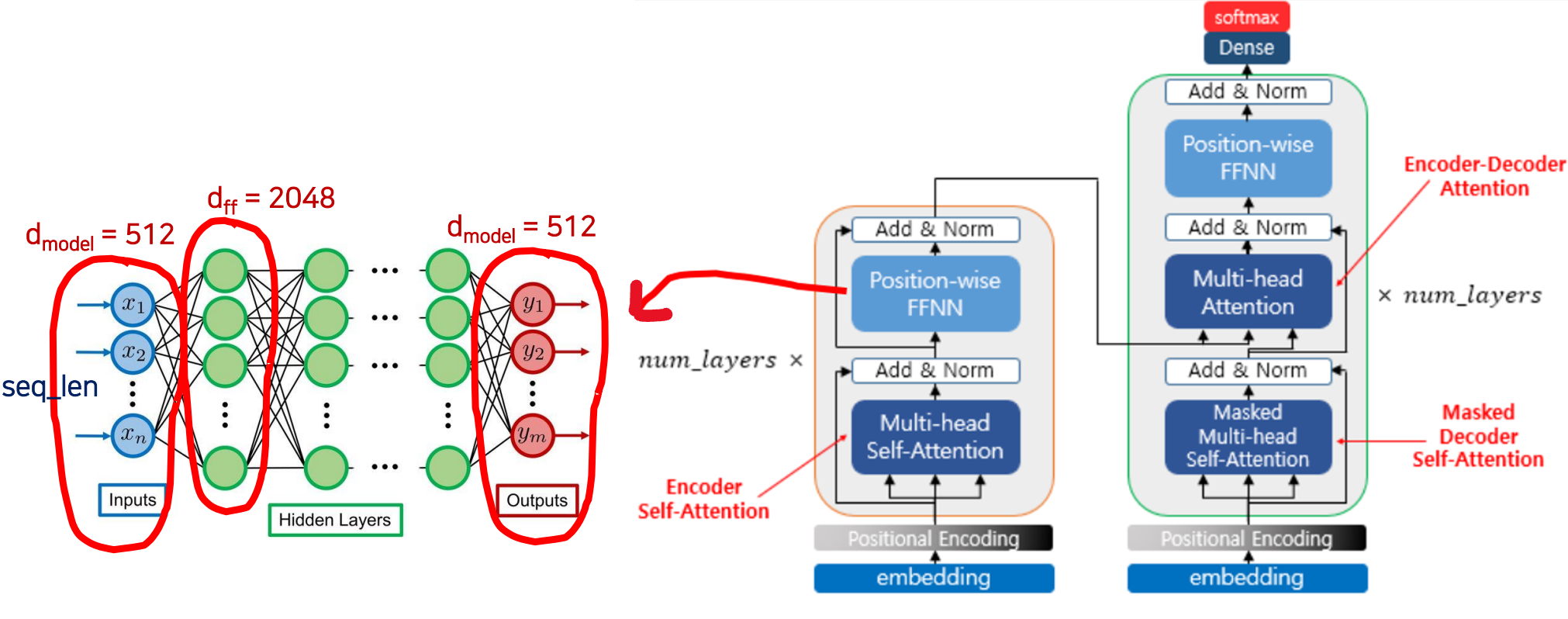
$d_{model}$ 은 모델의 전체 임베딩 차원을 나타내며, $d_k$ 는 멀티 헤드 어텐션에서 각 헤드의 어텐션 결과 차원을 나타냅니다. 8개의 헤드를 사용할 경우, 모든 헤드의 어텐션 결과를 합치면 $d_{model}$과 일치하는 512 차원의 어텐션 결과가 생성됩니다.

"I am a student"라는 문장을 모델에 입력으로 주면, 각 단어(토큰)는 512 차원의 임베딩 벡터를 가집니다. 따라서 전체 문장은 [4, 512] 차원을 가지게 됩니다. 이것은 모델의 입력 표현입니다.

멀티 헤드 어텐션을 사용할 경우, 각 헤드에서 "I"라는 단어에 대한 어텐션 결과의 차원은 64가 됩니다. 따라서 각 헤드에서 "I"에 대한 어텐션 결과는 [1, 64] 차원을 가집니다. 이것은 "I" 토큰에 대한 8개의 헤드에서의 어텐션 결과 중 하나입니다.

따라서 전체 멀티 헤드 어텐션 결과는 8개의 헤드에서 나온 어텐션 결과를 연결한 것이므로, "I" 토큰의 총 어텐션 결과 차원은 [8, 64]가 됩니다.

Key Hyperparameters and FFNN

• seq_len = 문장의 토큰 수
  • 9개의 토큰 x 8개의 문장(헤드)을 사용하므로 9 x 8 = 72
• d$_{model}$ = 512
  • 8개의 헤드가 모두 사용되었을 경우 8 x 64 = 512
• d$_{ff}$ = 2048
• FFNN Input 의 사이즈 = FFNN Output 의 사이즈 = d$_{model}$ = 512
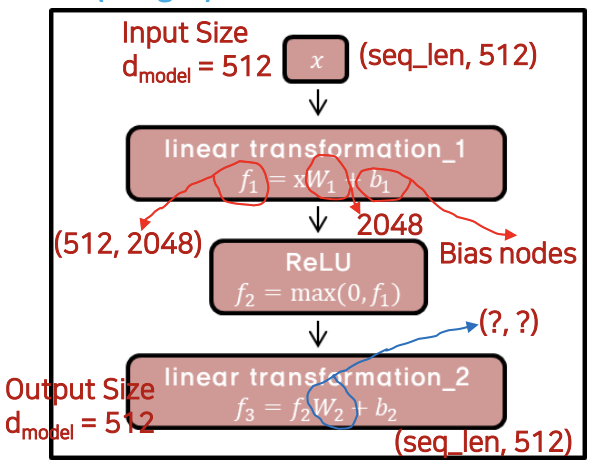
• W (weight) 의 Matrix Size 로 출력의 크기를 조절
  • linear transformation_1 이라는 sub layer 존재
  • linear transformation 는 matrix 의 차원을 조정할 떄 많이 사용
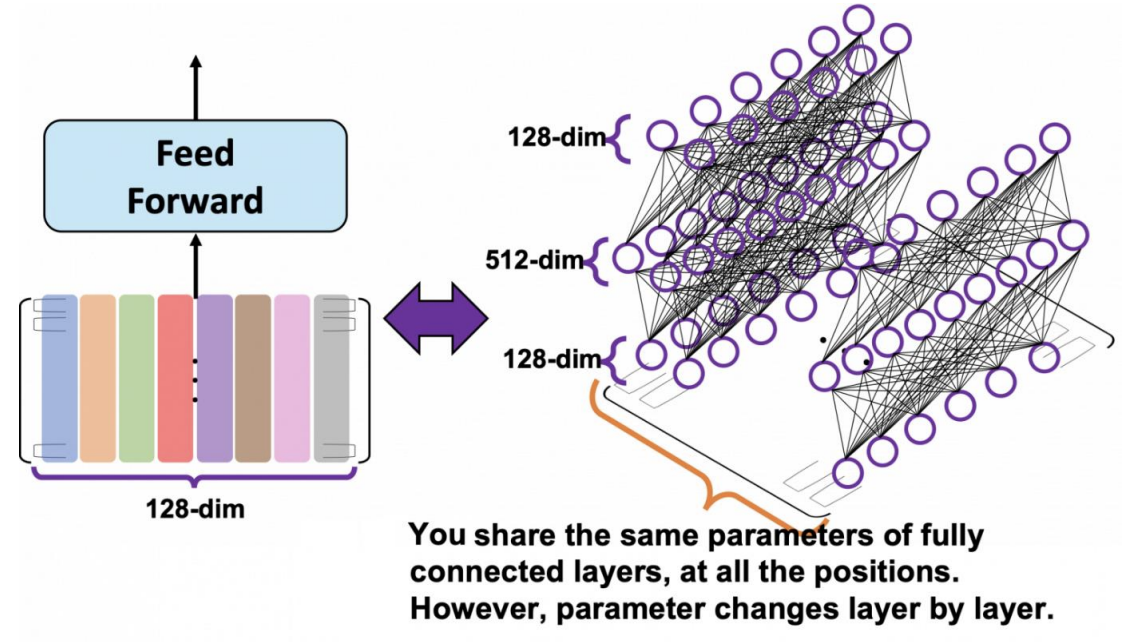
• you share the same parameters of fully connected layers, at all the positions.
  • 총 128 개의 토큰(단어)이 있다면, FFNN은 각각의 토큰마다 적용해준다 했으니. 는 FFNN 을 통해서 각각의 모든 토큰들의 weight 는 공유된다. (똑같은 것을 사용한다)
• However, parameter changes layer by layer.
  • 다음 단어(512-dim)로 갔을때는 값이 레이어마다 달라짐.
    
• 같은 문장이지만 해석을 다르게 하여 8개의 헤드 로 구성한다. (빨간색 동그라미)
• 한 헤드당, 한 토큰은 64 column 의 dimension 을 가진다
• 총 합하면 64 x 8 = 512 개의 Embedding vector 를 동시에 입력을 해서 training 시킨다.
• 전체 8개의 head 를 model 이라고 하는데, model 당 전체 차원(컬럼)은 512 이다.
  
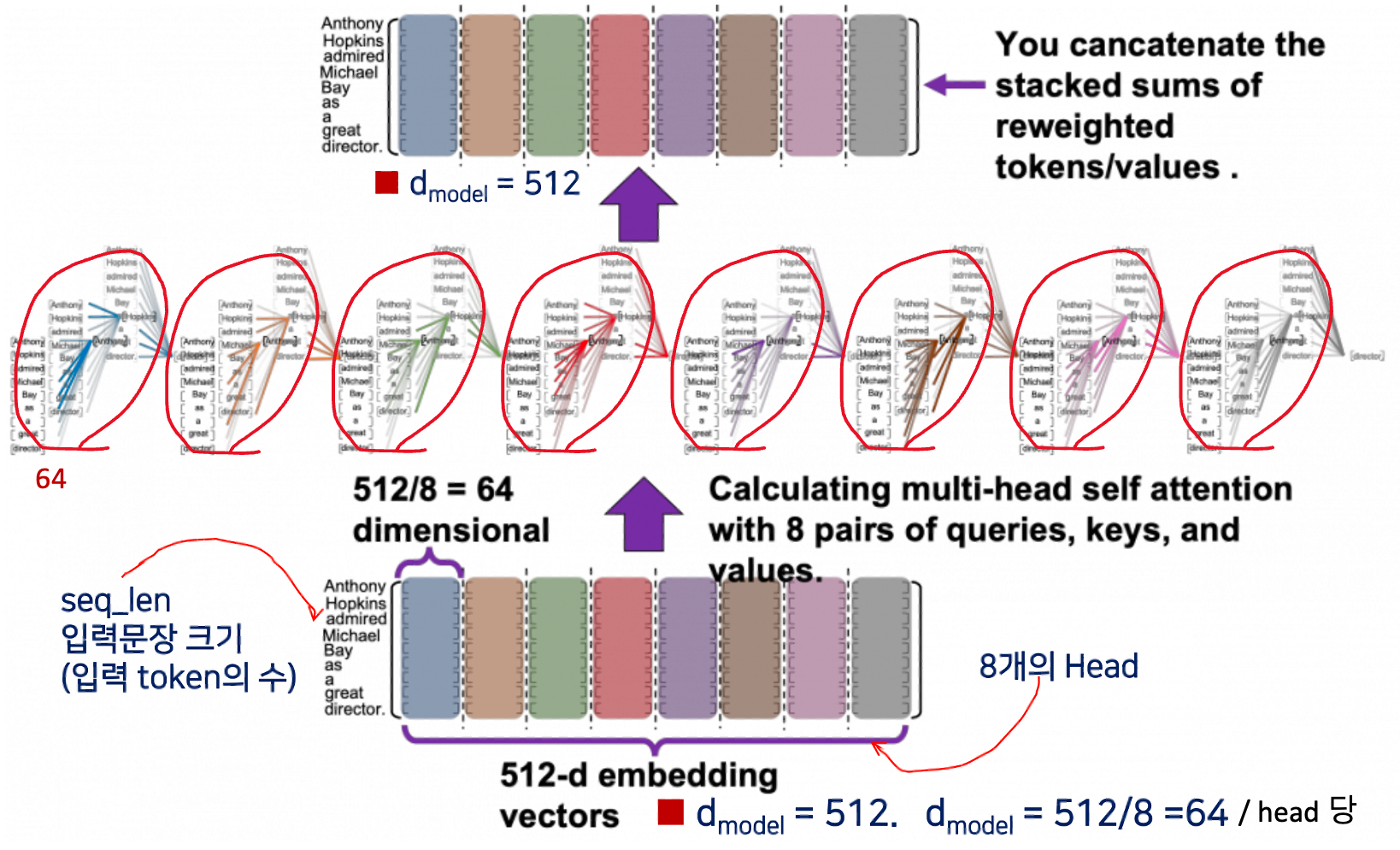
• 8개의 헤드가 입력이 되는데, 각각 독립적(attention #0, #1, ..., #num_heads)으로 학습이 되어서 총 헤드의 개수 num_heads 가 8이니까, 8번 수행한다.
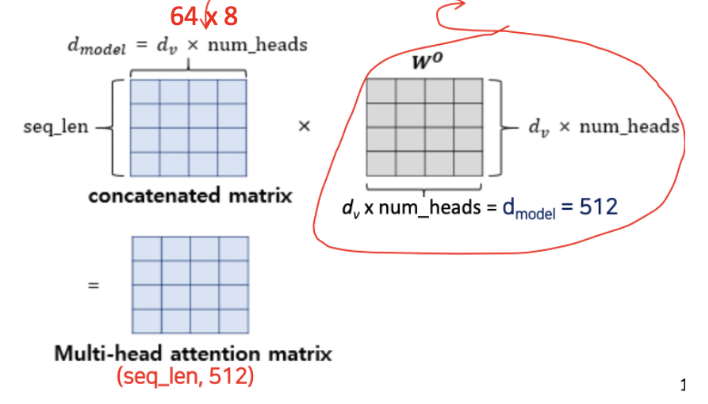
• 모든 Head들의 Attention Value 결과들을 모두다 합해 준다. 이것을 바로 concatenation 이라고 한다.
• d_v 는 64, num_heads = 8
• 여기에 weight 을 곱해줘야 하는데 최대 512 x 512 가 된다.
• 이런 weigh 이 곱해진것이 바로 최종 Muti-head attention matrix 가 되는 것이다.
  

---

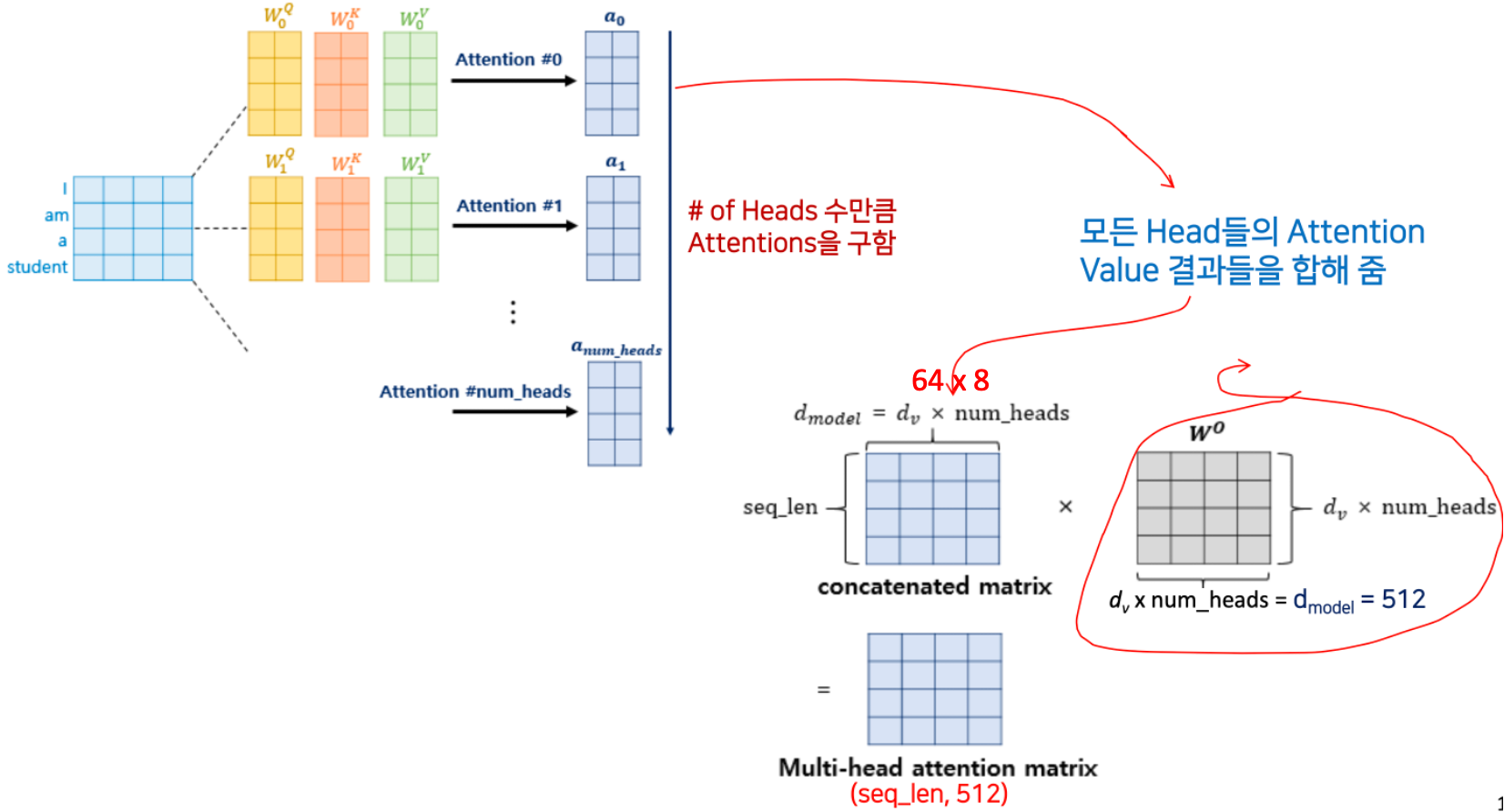
$d_{model}$이 512인 경우, 입력 시퀀스는 시퀀스의 각 위치(토큰)에 대해 512 차원의 임베딩 벡터를 가집니다. 따라서 입력의 차원은 [72, 512]가 됩니다.

FFNN에서 첫 번째 선형 변환을 수행하는 가중치 행렬 $W_1$는 모든 위치(토큰)에서 공유됩니다.

그러나 두 번째 선형 변환을 수행하는 가중치 행렬 $W_2$는 다른 레이어 간에 다르게 조정됩니다.

내가 이해한 것은 이렇게 아래의 그림에서는 $d_{model} = 512$ 라고 했었는데, 이렇게 홀수 짝수 나눠져있는 것은 각각은 헤드 하나를 나타내는 것이고,
위의 예시에서는, 하나의 헤드에 관한 Anthony라는 토큰의 차원이 64 라는 것이고 8개의 헤드니까 총
$d_{model} = 512$ 의 차원이다라고 이해하면 될 것 같다.

Linear Layer

• 1) Linear layer 는 matrix 또는 vector 의 크기를 감소시키거나 또는 증가시키는 역할을 한다.
  • 꼭 이게 weight matrix 가 아니라 대각선이 1이고 나머지는 0인 unit matrix 의 경우를 사용해서 사이즈를 의도적으로 줄일 때
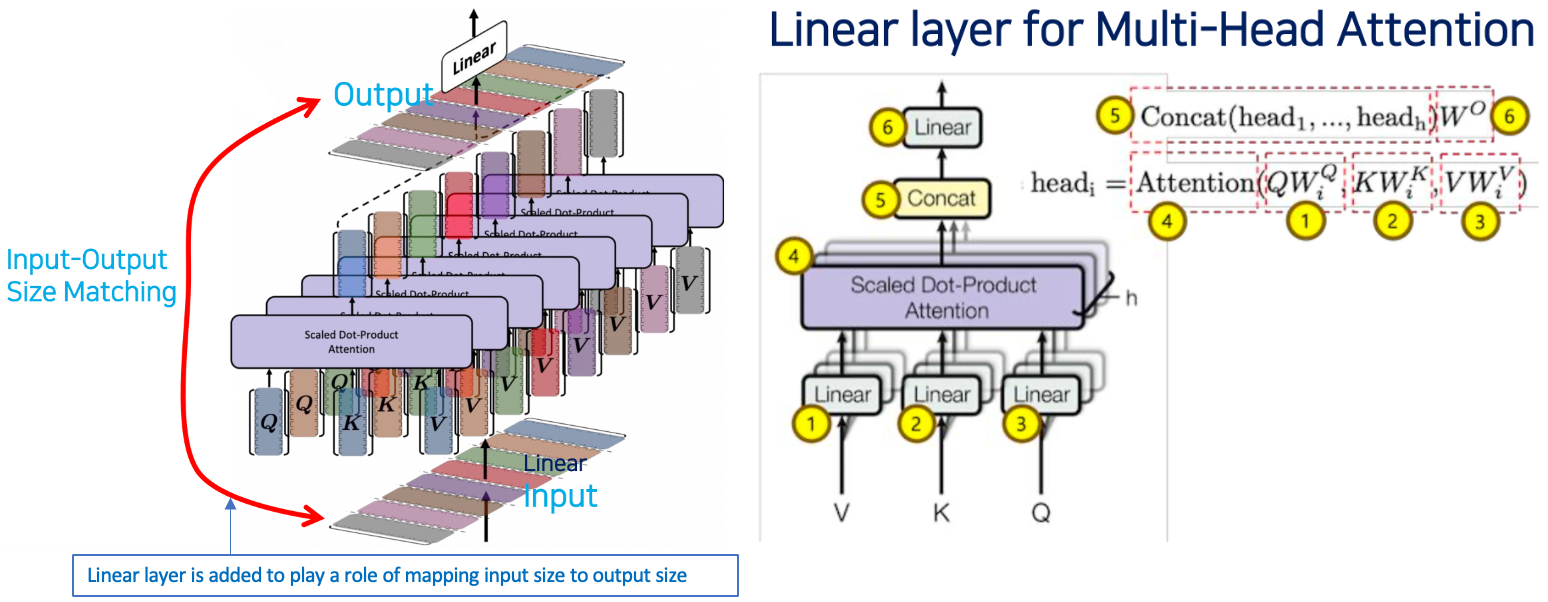
• 2) Linear layer 는 input 을 output 에 매핑(즉 사이즈를 맞춰주는)하는 역할을 수행하기 위해 추가된다.
  • (그림) Q, K, V 는 Weight ($W^Q$, $W^K$, $W^V$ $\leftarrow$ 이것을 training 시켜야함)을 곱해줘야하는데
  • Input 과 Output 사이즈 맞춰주기 : Input 이 $6 \times 5$ 인데, $6 \times 3$ 로 줄여야겠다면, $W^Q$ 값을 $5 \times 3$ 으로 설정
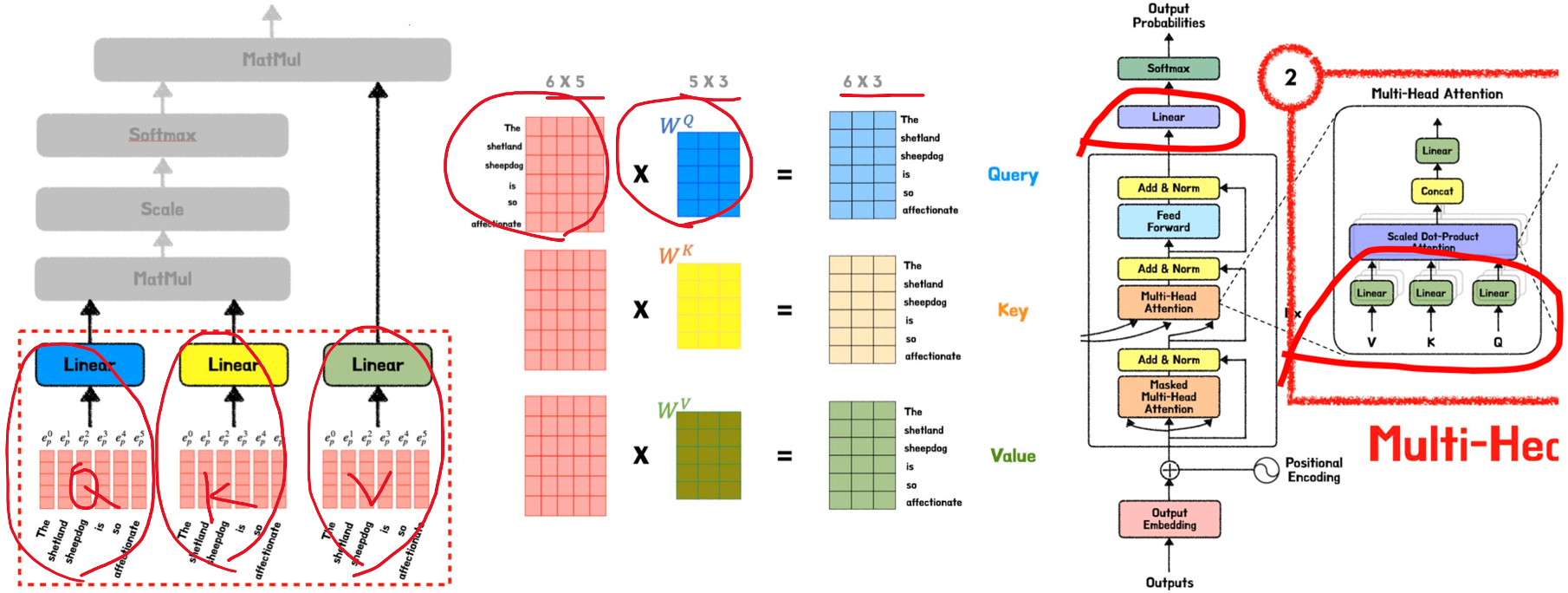
• 첫 번쨰 linear layer
  • ❶, ❷, ❸ : 각각의 Q, K, V 에 대해서 W 라는 weight matrix($W^Q, W^K ,W^V$) 로 linearization 을 통해 사이즈를 조정
• 두번째 linear layer
  • ❺ : 총 8개의 head 를 모두 concatenation
  • ❻ : $W^O$ 를 곱해줘 weight matrix 로 size 로 줄이는 단계
    

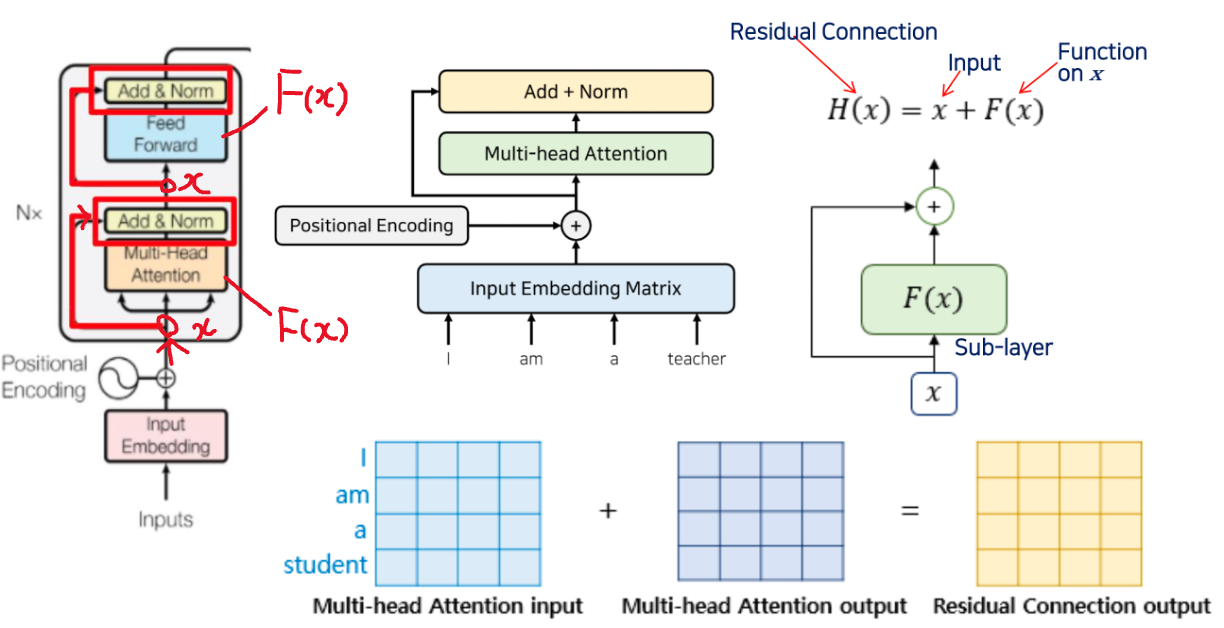
Residual Connection (Add) and Layer Normalization (Norm)

Residual Connection (Add)

• $H(x) = x + F(x) = x + Sub-layer = x + Multi-Head Attention$
  • input $x$ 를 어떤 함수 $F(x)$ 에 넣은 값과 더해주는 것.
  • 트랜스포머에서 $F(x)$ 는 Sub-layer 라 부른다.
  • 트랜스포머에서 $F(x)$ 에 해당하는 것
    • scaled dot product attention 즉 Mutli-head attention
    • Feedforward 도 하나의 $F(x)$ 이다.
• 특정 레이어를 건너 뛰어서 입력 (입력 데이터 + Self-Attention)
• 초기에 모델 수렴속도 높아짐

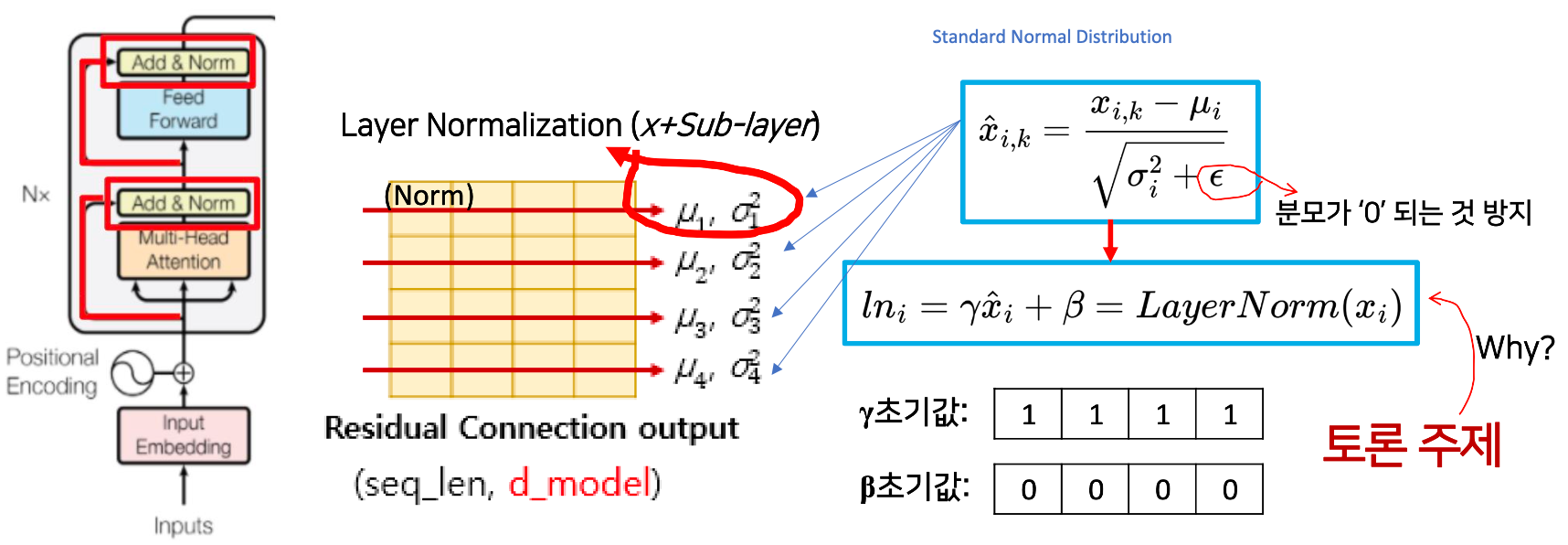
Layer Normalization (Norm)

• 각 레이어 값이 크게 변화(요동)치는 것 방지해서 모델이 빠르게 수렴(학습)하게 함
• Residual Connection 결과에 대해서 Normalization(정규화)
  
  
• Activation Function 과 유사 - Activation Func 은 FNNN에서 사용을 하였다.
• $\hat{x}_{i, k} = \frac{x_{i, k} - \mu_i}{\sqrt{\sigma_i^2} + \epsilon}$
  • 엡실론 $\epsilon$
    • 일반 Noraml Distribution 과 다르게
    • 분모의 $\sigma_i^2$ 즉, 분산의 값이 계속해서 작아질 수 있기 떄문에 분모가 0이 되는 것을 방지하고자 엡실론 값을 사용하였다.
  • 각각의 토큰마다 Normalization 해준다.
    • 첫 번째 토큰의 정규화 결과 : 평균은 $\mu_1$, 분산은 $\sigma_1^2$ 두번쨰 ...
    • 그렇다면 이렇게 한 것에 $\gamma, \beta$ 는 왜 곱하고 더해줄까? (토론주제)
• $ln_i = \gamma \hat{x}_i + \beta = Layer \ Norm(x_i)$
  • Noramlization 된 것($\hat{x}_i$) 을 다시 $\gamma$ coefficient 와 $\beta$ bias 값을 함수 형태로 만들어준것이 바로 layer normalization
  • $\gamma$ 의 초기값은 $[1,1,1,1]$, $\beta$ 의 초기값은 $[0,0,0,0]$ $\to$ 둘다 업데이트 될 예정

train 과정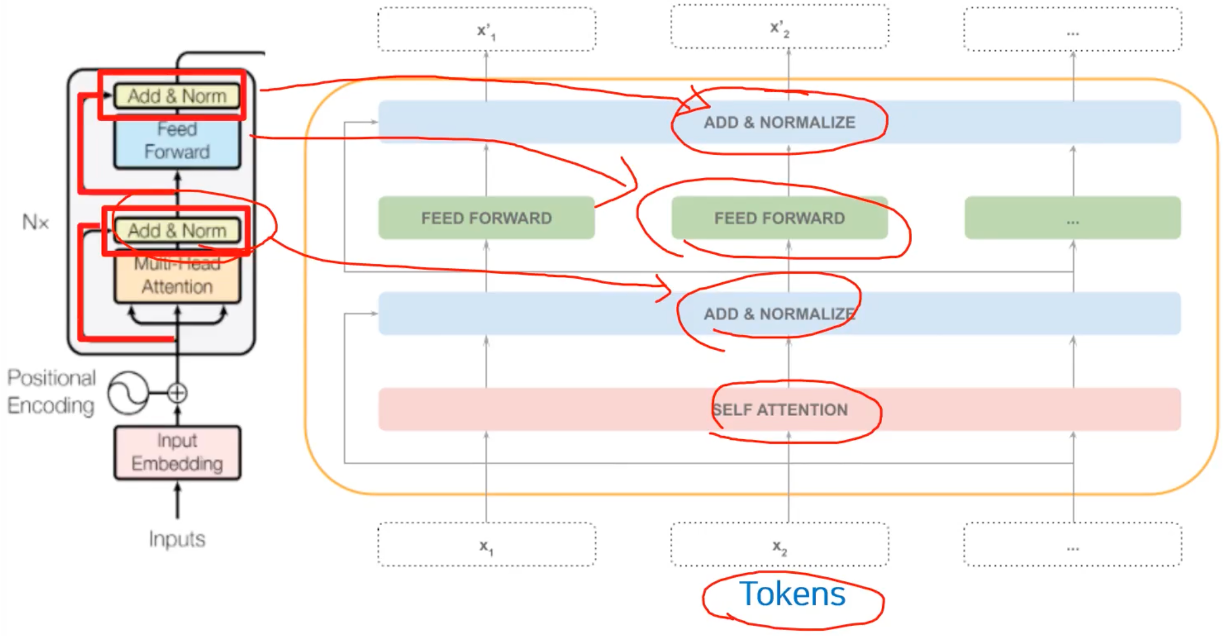

Key Algorithms in Layers/Sub-Layers of Transformer

빨간색 사각형을 친 부분을 떄로는 Attentio(Q, K, V) 라고 한다.
즉 Scaled Dot-Product Attention 을 구하는 것이 가장 핵심이다.