정의
-
특정한 조건에 맞는 원소들의 모임
-
특징
- 순서가 없음
- 같은 원소 개수는 집합에 영향x
- ex) s = {a,b,c,d} = {a,b,d,b,c,d,d,d}
- 집합은 집합을 원소로 가질 수 있음
- ex) s= {a,b,{1,2,3},{e,a,c},9}
-
용어
- 원소(element, member): 집합의 object
- {1,5,5,3,1} = {1,3,5}
- 부분집합(subset)
- T ⊆ S: t의 모든 원소가 s에 포함 될때 --> t는 s의 부분집합임
- ⊂는 진부분 집합 의미
- T ⊆ S: t의 모든 원소가 s에 포함 될때 --> t는 s의 부분집합임
- proper subset(진부분 집합)
- a ⊆ b, but a ≠ b ==> ⊂
- ∀𝑥 (𝑥∈𝐴 → 𝑥∈𝐵) ∧ ∃𝑥(𝑥∈𝐵 ∧ 𝑥∉𝐴)
- caldinality: 집합 크기, 집합 원소의 수
- 기호: |A| --> 집합 들어옴
- cf) 절대값 |-2|=2 랑 다름 --> 정수 들어옴
- ex) |∅| = 0, |{∅}|=1
- 기호: |A| --> 집합 들어옴
- tuple: 순서 있는 특정한 원소 모임
- 순서쌍: 2개의 튜플
- 곱집합(cartesian product): 집합 A, B에 대하여 순서쌍 (a,b)의 집합
- 교환법칙 성립x --> aXb와 bXa의 결과는 다름


- 교환법칙 성립x --> aXb와 bXa의 결과는 다름
- truth set: 술어가 참인 도메인의 모든 값의 집합
- 주어, 술어
- ex) she is a student
- 주어: she -> x
- 술어: is a student -> P(x)
- product: 곱셈 연산의 결과가 되는 값
- 원소(element, member): 집합의 object
-
기호

- S = {x|설명 or 조건}의 형태 가짐
- 구간
- [a,b]: a<= x <=b
- (a,b): a< x < b
- U: 전체 집합
- ∅ or {}: 공집합
- 모든 집합의 부분 집합
- ∅ ⊂ 모든 집합
- ∅ ∈ 모든 집합 --> 공집합이 원소는 아니므로 성립x
- ∅ ⊂ 모든 집합
- {∅}과는 다름 --> 원소 공집합인 경우임, 원소 1개
- 모든 집합의 부분 집합
- 집합 equal(=): 같은 원소들을 가지는 경우
- a=b <-> a ⊆ b and b ⊆ a
-
중요 집합

whole number: 0과 자연수
- 집합 연산
- union(합집합): a ∪ b
- intersection(교집합): a ∩ b
- disjoint(서로소 집합): 교집합이 공집합
- complement(여집합)
- A의 여집합: U - A
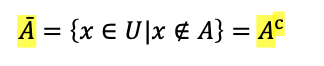
- A의 여집합: U - A
- difference(차집합): a-b
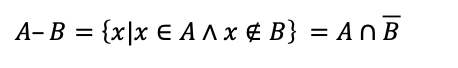
- caldinality of the union of two sets(합집합 개수)
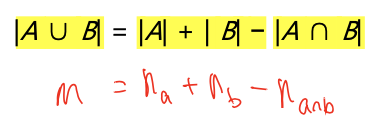
- 집합 항등식
- Distributive laws
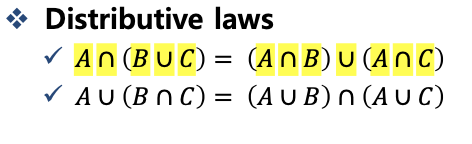
- De Morgan’s laws
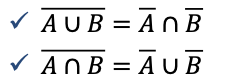
- Absorption laws
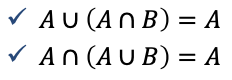
- Distributive laws
- 집합 문제 풀이법
-
집합이 다른 집합의 부분집합임을 이용
- x ∈ a 등 원소를 이용
- 명제 문제랑은 풀이가 조금 다름
-
명제 논리 이용
-
membership table 이용
1: set안에 원소임, 0: set안에 원소 아님

-