이산수학
1.proposition(명제)

해당 이산수학 내용은 한동대 이원형 교수님 수업을 들으며 정리한 내용입니다.1\. 내용이 참인지 거짓인지 판별할 수 있는 문장 또는 식(=statement)2\. implication(->) : p->q 1\. p: hypothesis 2\. q: conclusi
2.기초
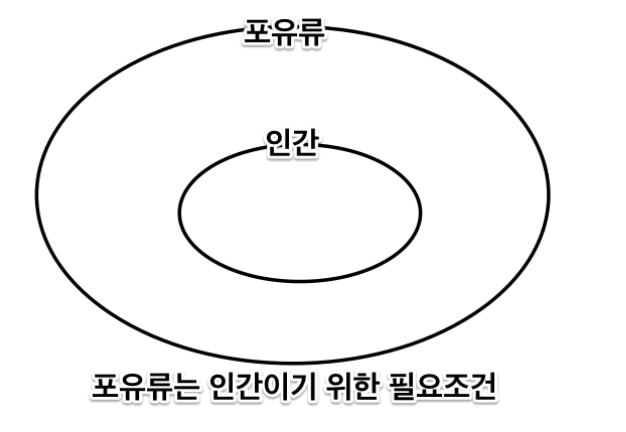
필요 조건 1\. b if a: a->b충분 조건 1\. a only if b: a->b필요충분조건a->b 이면서 b->a인 경우 a와 b가 완전히 같은 경우(=동치) ==> a는 b를 위한 필요충분조건
3.Set(집합)

특정한 조건에 맞는 원소들의 모임특징순서가 없음같은 원소 개수는 집합에 영향xex) s = {a,b,c,d} = {a,b,d,b,c,d,d,d}집합은 집합을 원소로 가질 수 있음ex) s= {a,b,{1,2,3},{e,a,c},9}용어원소(element, member)
4.quantifier(한정자)

정의: all과 some을 어떻게 나타내는가종류∀: for allfor all x, P(x)∃: there existsfor some x, P(x)for at least one x, P(x)우선순위가장 높음ex) ∀x P(x)∨ Q(x) --> (∀x P(x)) ∨ Q
5.함수
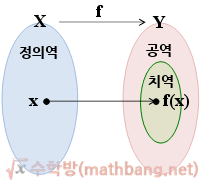
하나의 원소에 하나의 원소가 대응하는 것용어정의역(domain): X를 f의 정의역공역(codomain): Y를 f의 공역치역(range): 함숫값 f(x)를 원소로 하는 집합상(image): 집합 X의 원소 x에 대응하는 집합 Y의 원소 y를 상(함숫값)이라고 함 원
6.추론
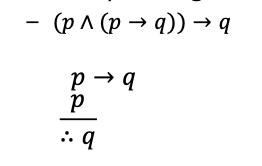
용어추론(inference): 참으로 알려진 명제를 기초로하여 다른 명제를 유도하는 과정전제(premise): 결론의 근거를 제공하는 명제명제들 중 결론을 제외한 명제명제(statement): 참과 거짓 판별할 수 있는 문장결론(conclusion): 새로 유도된 명제
7.how to prove

용어threorem(정리): 증명을 통해 참임이 밝혀진 명제axiom(공리): 스스로가 참인 명제보통 정리는 다른 정리를 사용하여 증명하지만, 자꾸 거슬러 올라가다 보면 출발점이 되는 명제가 있음 --> 이러한 증명하지는 못하지만 참이라고 인정해야 하는 명제가 공리임l
8.recursion

기본 2단계basic step: 0번째 함수값recursive step: 일반항기본 2단계 1\. basic step: 초기 집합 원소 2\. recursive step: 새로운 집합에 대한 rulestring용어λ: null stringX∗: λ를 포함한 x의