기초
- 용어
- threorem(정리): 증명을 통해 참임이 밝혀진 명제
- axiom(공리): 스스로가 참인 명제
- 보통 정리는 다른 정리를 사용하여 증명하지만, 자꾸 거슬러 올라가다 보면 출발점이 되는 명제가 있음 --> 이러한 증명하지는 못하지만 참이라고 인정해야 하는 명제가 공리임
- lemma(부명제): 정리를 증명하는 과정에서 필요한 중간 다리
- corollary(따름 정리): 어떤 정리가 증명되었을 때, 그것으로부터 만족하는 성질들
- conjecture(추측): 참이라고 제안 되어진 명제
- 증명 방식(p->q)
- 직접 증명 시도
- 간접 증명 시도
- 추가 증명 방식 사용(정방향 추론 -> 역방향 추론)
- forward reasoning(정방향 추론)
- backward reasoning(역방향 추론)
- 추론의 시작점을 결론으로 하여 하위 목표들이 참임을 증명

- 추론의 시작점을 결론으로 하여 하위 목표들이 참임을 증명
증명 종류
- trivial proof(사소한 증명)

- vacous proof(공허한 증명)

- direct proof(직접 증명)
- 명제를 변형하지 않고 p->q가 참임을 증명
- indirect proof(간접 증명): 직접 증명하지 않고 간접적으로 증명
- Proof by Contraposition(대우 증명)
- 대우를 이용하여 증명
- proof by contradiction(모순 증명)
- 주어진 문제의 명제를 부정해 놓고 논리를 전개하여, 그것이 모순됨을 보임 --> 본래의 명제가 참임을 증명
- p→q ≡ (p∧¬q)를 이용해 증명
- Proof by Contraposition(대우 증명)
- 추가 증명 방식

- proof by cases(사례에 의한 증명)
- 모든 사례에 대해 증명
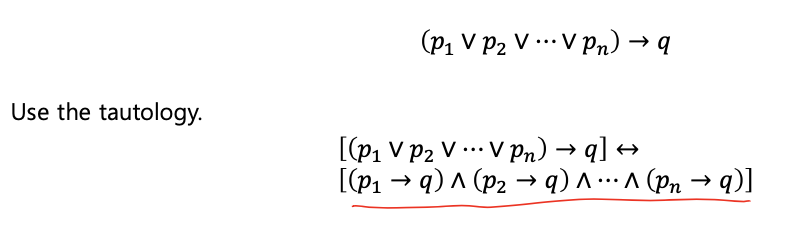
- 모든 사례에 대해 증명
- existence proof(존재 증명)
- ∃𝑥 𝑃(𝑥) --> 한가지 경우를 찾아 참임을 증명
- proof by counterexample(반례)
- ∃𝑥 ¬𝑃(𝑥) ≡ ¬∀𝑥 𝑃(𝑥)
- uniqueness proof(유일성 증명)
- 명제가 유일한 원소를 가짐
- 기호: ∃!x P(x)
- 유일성과 존재성은 다른 것임
- 명제가 유일한 원소를 가짐
- Universally Quantified Assertions
- ∀𝑥 𝑃(𝑥) 증명 ==> P(x)의 임의의 x에 대하여 모두 성립함을 보임
- proof by cases(사례에 의한 증명)
