본 딥러닝도 다시보자 02: Bayesian Rule

이 글은 공돌이의 수학 강의노트 사이트에 게시된 "베이즈 정리의 의미"를 참고해서 쓴 글입니다. 작성자가 제시한 Attribution-NonCommercial 4.0 International 라이센스를 준수하였음을 명시합니다.

Bayesian Rule

A method to update belief on the basis of new information.
새로운 정보를 토대로 어떤 사건이 발생했다는 주장에 대한 신뢰도 갱신방법

- H : hypothesis, 어떤 일이 발생했다는 주장
- E : evidence, 새로운 정보
- P(H) : prior, 어떤 일이 발생했다는 주장의 신뢰도
- P(H|E) : posterior, 새로운 정보를 받은 후에 갱신된 신뢰도

evidence를 관측해서 갱신하기 전 후의 주장에 대한 신뢰도 간의 관계식은 다음과 같은 식으로 나타낼 수 있을 것이다. 이 식은 우리가 흔히 Bayesian Rule 공식이라고 말하는 그 식이다.

evidence를 관측해서 갱신하기 전 후의 주장에 대한 신뢰도 간의 관계식 이라는 건 다시 말하자면, prior와 posterior 간의 관계를 의미한다.

불확실성이 있는 prior를, 즉 어떤 일이 발생했다는 주장의 신뢰도를 새로운 정보를 바탕으로 어떻게 갱신할 수 있을까? 짧은 예시를 통해서 신뢰도를 갱신하는 bayesian rule을 이해해보자.

Example of Bayesian Rule

질병 A에 의 발병률(Attack rate) : 0.1%
질병 A에 실제로 걸렸을 때, 질병이 있다고 검진할 확률 (Sensitivity): 99%
질병 A에 실제로 걸리지 않았을 때, 질병이 없다고 검진할 확률 (Specificity): 98%

만약에 어떤 사람이 질병 A에 걸렸다고 검진 받았을 때, 질병 A에 실제로 걸렸을 확률은 어떻게 될까?

이 예시 문제에 대해서 hypothesis와 evidence를 정의하면 다음과 같다.

• Hypothesis : 실제로 질병 A에 걸렸다. >> True
• Evidence : 질병이 있다고 진단받았다. >> Positive

그렇다면 위의 정의한 True와 Positive로 confusion matrix를 정의해보자.

• True Positive(TP) : 질병 A에 실제로 걸렸을 때, 질병이 있다고 검진할 확률
• True Negative(TN) : 질병 A에 실제로 걸렸을 때, 질병이 없다고 검진할 확률
• False Positive(FP) : 질병 A에 실제로 걸리지 않았을 때, 질병이 있다고 검진할 확률
• False Negative(FN) : 질병 A에 실제로 걸리지 않았을 때, 질병이 없다고 검진할 확률

따라서, 기본적으로 질병 A의 발병률은 0.1%이므로 임의의 사람이 이 질병에 걸렸을 확률은 $P(H) = 0.001$ 이다. 그리고 sensitivity에 해당하는 True Positive(TP)는 $P(E|H)$로, $P(E|H) = 0.99$라고 할 수 있다. specificity에 해당하는 True Negative(TN)는 $P(E|H)$로, $P(E^c|H^c) = 0.98$ 이다.

이를 그림으로 시각화하게 되면, 다음과 같다.

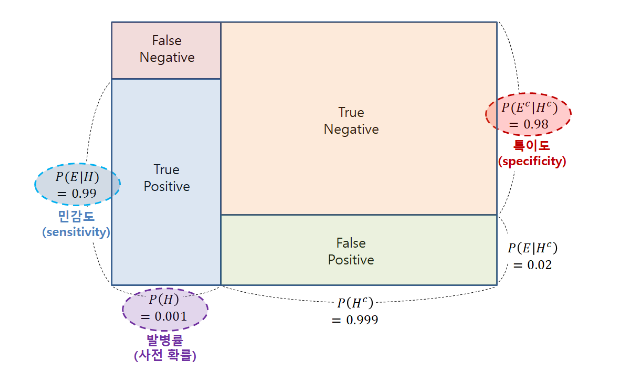
[이미지 출처: 공돌이의 수학 정리 노트 "베이즈 정리의 의미"]

다시 처음의 식으로 돌아와서 식을 정리해보자.

$P(E)$는 "질병이 있다고 진단받았다.(positive)"이므로, TP(True Positive)와 FP(False Positive)의 합으로도 표현할 수 있다. 다시말하면 질병에 실제로 걸렸던 걸리지 않았던 질병이 있다고 진단받은 확률이라고 보면 된다.

$P(E) = P(E|H)P(H) + P(E|H^c)P(H^c)$

식을 다시 정리해보면 아래의 식과 같고, 아래의 식에 실제 확률을 대입해서 계산할 수 있다.

(소수점 아래 셋째자리 반올림한 값)

이렇게 처음 구한 신뢰도를 어떻게 갱신해 나갈 수 있을까?

P(H), 어떤 일이 발생했다는 주장의 신뢰도 (prior)를 갱신할 수 있는 방법은 앞에서 구한 posteiror, P(H|E)의 값을 prior (P(H))로 이용해서 posterior를 갱신할 수 있다.

그림으로 이 말을 확인해보면 다음과 같이 P(H)가 이전에 구했던 P(H|E)값인 0.047로 변해있는 것을 볼 수 있다.

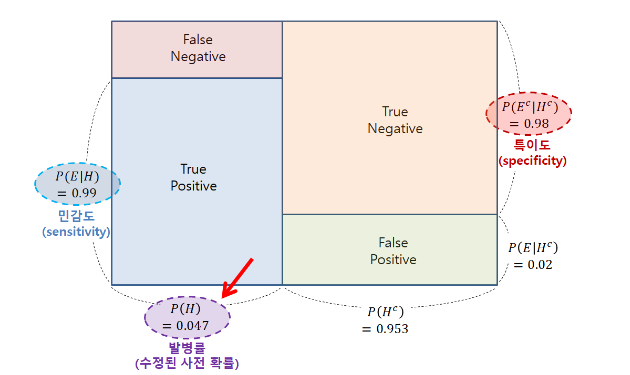
[이미지 출처: 공돌이의 수학 정리 노트 "베이즈 정리의 의미"]

갱신된 prior로 posterior, 신뢰도를 갱신시켜보자.

(소수점 아래 셋째자리 반올림한 값)

처음에 구한 신뢰도(posterior, P(H|E))는 4.7% 였으나, 질병에 걸렸다는 사실, prior (P(H))를 갱신시켜줌으로써 두번째에 구한 신뢰도는 70.9%로 갱신되었다. 즉, 70%의 신뢰도로 질병 A에 걸렸다고 말할 수 있다는 것이다.

이것이 베이지안 확률론이 기존의 통계학과는 다른 점이다. 기존의 통계학 같은 경우, 확률공간이나 모집단, 표본 집단의 분포를 정확하게 정의하고 그를 이용해 확률을 계산한다. 그러나 베이지안 확률론은 prior와 같은 경험에 기반한 불확실성이 있는 수치를 기반으로 추가 정보들과 함께 prior를 갱신해 나간다.