본 딥러닝도 다시보자 01: Markov Chain Process

Gahyeon Kim·2023년 1월 27일

본 딥러닝도 다시보자

목록 보기

1/3

이 글은 iAI LAB, POSTECH에서 게시한 Markov chain강의를 참고해서 쓴 글입니다. 유튜브 영상 하단 더보기란에 강의 자료 ppt를 볼 수 있는 링크가 있습니다.

Markov chain에 대해서 찾아보면 다들 간단하게 설명한 내용들 밖에 없어서 직접 유튜브에 올려진 강의를 듣고 꼼꼼히 정리해보려고 한다. 시간이 있다면 강의를 들어보는 걸 추천한다.

Sequential Process

"시계열 데이터(sequential data)를 핸들링하는 방법"
시스템(system)을 연속적으로 보는 것이 아니라, N개의 "discrete한 상태(state)"들로 본다. 연속적인 건 핸들링할 수 없기 때문이다.

q \in {\{s_1, s_2, s_3 \cdots s_N}\}

N개의 discrete한 state들을 시간 순서대로, 1부터 순서대로 진행한다면 deterministic하고, random하게 state를 돌아다닐 수 있게 만들면 stochastic 하다. 예를 들어서 날씨를 생각해보면, 오늘의 날씨가 어떻든 내일의 날씨는 random하게 결정되기 때문에 stochstic system으로 표현할 수 있을 것이다.

ideal한 상황에서 0 부터 T까지의 시간동안 시계열 데이터가 generate된 확률을 아래처럼 나타낼 수 있을 것이다. 시계열 데이터는 시간의 영향을 받기 때문에 이전 데이터의 영향도 받게 된다. 그래서 조건부 확률로 식을 나타낼 수 있는데, 이 식을 계산하기는 불가능에 가깝다.

p{(q_0,q_1,\cdots,q_T)} = p(q_0)\,p(q_1|q_0)\,p(q_2|q_0,q_1)\,p(q_3|q_0,q_1,q_2)\cdots

Markov Chain

그래서 Andrey Markov가 "바로 이전 상태만 지금 상태에 영향을 줄 수 있다" 라고 말하고 식을 과감히 잘라냈다. 이전의 모든 상태들을 고려해서 계산하는 것이 불가능하기 때문에 바로 이전의 상태를 이용해서 apporximation하는 것이다. 이 방법이 거의 불가능에 가까웠던 계산을 "tractable" 하게 만들어주었다.

p{(q_t+1|\,q_t\cdots q_0)}\, \fallingdotseq \,p(\,q_t+1|\,q_t)

p{(q_0,q_1,\cdots,q_T)} = p(q_0)\,p(q_1|q_0)\,p(q_2|q_1)\,p(q_3|q_2) \cdots

Markovian Property

"현재의 state가 과거의 states, 즉 누적된 history의 충분한 통계적인 정보의 축적으로 보고, 다음 state(future)를 구하기 위해서는 현재의 state만 있어도 충분하다." 라고 생각한다. 굳이 누적된 과거의 정보를 일일이 따지지 않아도 된다는 거다.

p{(q_t+1|\,q_t\cdots q_0)}\, = \,p(\,q_t+1|\,q_t)

p{(q_t+1 = s_j|\,q_t = s_i)}\,= \,p(q_t+1 = s_j|\,q_t = s_i)

State Transition Matrix

현재 state를 $s'$ , 다음 state를 $s$ 라고 했을 때 $s'$ 에서 $s$ 로 이동하는 state transition probability는 다음과 같다.

P_{ss'} = P{[s_{t+1} = s' |\,s_t = s ]}

state 1( $s_1$ )부터 state N( $s_N$ )까지의 상태가 있을 때 random한 임의의 state로 부터 다음 state로 갈 state transition probability들로 이뤄져 있는 N X N 행렬을 state transition matrix라고 한다. $\mathcal{P_{11}}$ 는 $s_1$ 에서 $s_1$ 으로 이동할 확률 일 거고, $\mathcal{P_{n1}}$ 은 $s_1$ 에서 $s_N$ 으로 이동할 확률일 것이다. 이때 주의 할 것은 하나의 state에서 state로 이동하는 event가 발생할 확률을 구하는 것이 아니라, 그러한 event 들이 발생함으로써 시계열 데이터가 나오는 확률을 구하는 것이다.

\mathcal{P} = \begin{bmatrix}\mathcal{P_{11}}\cdots\mathcal{P_{1n}}\\\vdots\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\vdots\\{P_{n1}}\cdots{P_{nn}}\\ \end{bmatrix}

시계열 state의 sequence가 generating 되고, 이에 따라 확률로 이뤄진 matrix도 계속 다르게 generate되기 때문에 stochastic data가 만들어진다고 할 수 있다.

Markov Process

Definition

agent가 있을 수 있는 state의 상태는 discrete하고, finite 하다.
다른 state로 transition 하는 deterministic 하지 않고, 확률(transition probability)로 정의되어 있다. $P = {\{p_{ij}}\}_{M \times M}, \,\,\,\,\,\,\, 1 \le i,j \le M$
initial state에 있을 확률은 $\pi$ 이다. $\pi = {\{\pi_i}\}$
Markov process는 memoryless random process이다.
바로 이전 상태만 지금 상태에 영향을 줄 수 있고, 그 전의 상태들의 변화는 랜덤하다.
passive stochastic behavior로 진행된다.
외부의 힘 없이 한번 Markov chain 에 들어가게 되면 그 다음부터는 passive하게 진행된다. 그러면서 passive stochastic sequence가 발생하게 된다.

Property of P Matrix

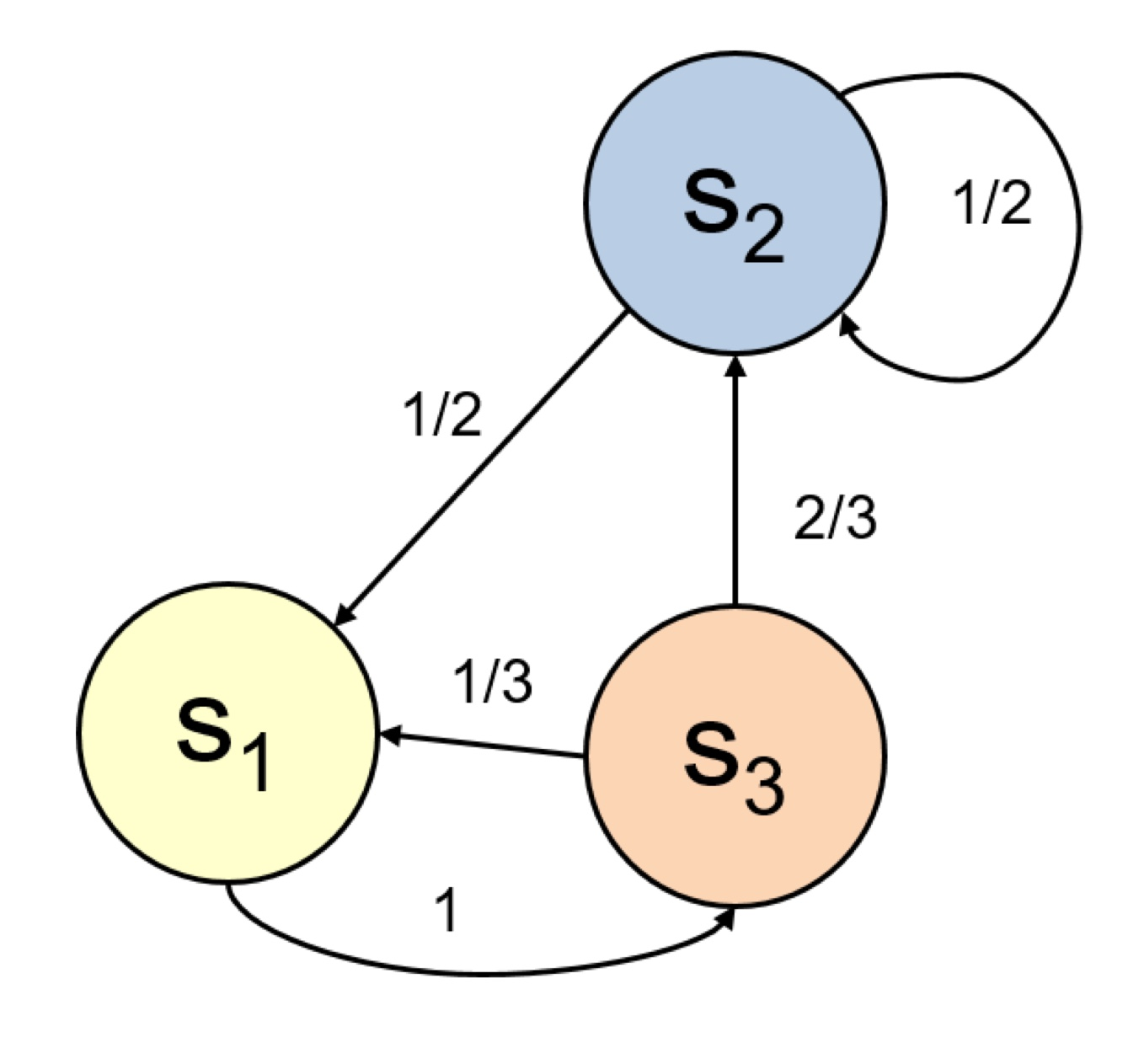$s_1$ , $s_2$ , $s_3$ 3개의 state가 있는 Markov chain(MC) 예시를 통해서 P가 의미하는 바를 알아보자.

\sum_{j \in S}^N {p_{ij}} = 1

P matrix에서 각각의 행을 모두 더했을 때의 값은 당연히 1이다. 다시 말하면 현재 state에서 다음 random한 임의의 state로 갈 확률의 총합이 1이라는 것이다.

{P} = \begin{bmatrix}{p_{11}}&{p_{12}}&{p_{13}}\\{p_{21}}&{p_{22}}&{p_{23}}\\{p_{31}}&{p_{32}}&{p_{33}}\end{bmatrix} = \begin{bmatrix}{0}&{0}&{1}\\{1\over2}&{1\over2}&{0}\\{1\over3}&{2\over3}&{0}\end{bmatrix}

$P^n$ 은 n번 transition 했을 때의 prior state에서 later state로 갈 확률을 의미한다. $P^n$ 의 의미는 아래의 Champman-Kolomogorov Equation을 보면 더 잘 이해할 수 있을 것이다.

Champman-Kolomogorov Equation

1-step transition probabilities
$1^{st}$ state의 probability distribution은 열 벡터(row vector)로 된 initial state(zero state)에 transition probability matrix P와의 곱으로 표현될 수 있다.

\begin{bmatrix}\Pi^{(1)}_1&\Pi^{(1)}_2&\Pi^{(1)}_3\end{bmatrix} = \begin{bmatrix}\Pi^{(0)}_1&\Pi^{(0)}_2&\Pi^{(0)}_3\end{bmatrix} \begin{bmatrix}{P_{11}}&{P_{12}}&{P_{13}}\\{P_{21}}&{P_{22}}&{P_{23}}\\{P_{31}}&{P_{32}}&{P_{33}}\end{bmatrix}

row 벡터와 column 벡터를 곱해서 $\Pi^{(1)}_1$ , $\Pi^{(1)}_2$ , $\Pi^{(1)}_3$ 을 구하게 된다.

\Pi^{(1)}_1 = \Pi^{(0)}_1P_{11} + \Pi^{(0)}_2P_{21} + \Pi^{(0)}_3P_{31}

이 식을 물리적으로 해석하면 다음과 같다.

LHS
$\Pi^{(0)}_1P_{11}$ : 1에서 1로 transition할 확률
$\Pi^{(0)}_2P_{21}$ : 2에서 1로 transition할 확률
$\Pi^{(0)}_3P_{31}$ : 3에서 1로 transition할 확률
결국 현재의 어떤 상태에서 "1"로 갈 확률을 말한다.
RHS
$\begin{bmatrix}\Pi^{(0)}_1&\Pi^{(0)}_2&\Pi^{(0)}_3\end{bmatrix}$ : initial state ${\{\pi^{(0)}_i}\}$ 에서 agent가 각 state에 있을 확률
P: state transition matrix

즉, $\begin{bmatrix}\Pi^{(1)}_1&\Pi^{(1)}_2&\Pi^{(1)}_3\end{bmatrix}$ 는 initial state에서 agent가 각 state에 있을 확률을 1번 state transition 한 뒤에, 각 state에 agent가 있을 확률 분포를 의미한다.

2-step transition probabilities
그럼 2번 transition을 했을 때는 어떻게 될까?

\begin{bmatrix}\Pi^{(2)}_1&\Pi^{(2)}_2&\Pi^{(2)}_3\end{bmatrix} = \begin{bmatrix}\Pi^{(1)}_1&\Pi^{(1)}_2&\Pi^{(1)}_3\end{bmatrix}P = \begin{bmatrix}\Pi^{(0)}_1&\Pi^{(0)}_2&\Pi^{(0)}_3\end{bmatrix}P^2

식을 해석해보자. 각 state에 agent가 있을 확률은 첫번째 transition을 한 확률에 P를 곱한 것과 같다. 그런데 위의 1-step transition의 경우에서 구했다시피,

\begin{bmatrix}\Pi^{(1)}_1&\Pi^{(1)}_2&\Pi^{(1)}_3\end{bmatrix} = \begin{bmatrix}\Pi^{(0)}_1&\Pi^{(0)}_2&\Pi^{(0)}_3\end{bmatrix}P

이기 때문에 initial state에서의 확률에 $P^2$ 을 곱해준 것과 같다. $P^2$ 는 $P$ 와는 또 다른 3X3 행렬로, 2번 transition해서 $2^{nd}$ state로 가게 될 확률을 의미한다. 예를 들어서 1에서 3으로 이동할때 2번 transition하는 걸 생각해보면, 1>2>3 도 2번의 transition을 거쳐 state이동을 했고, 1>1>3도 동일하게 2번의 transition을 거쳐 state이동을 했다고 할 수 있다.

n-step transition probabilities
바로 이어서 n step transition을 한 경우를 생각해보자, initial state에서 agent가 각 state에 있을 확률을 n번 state transition 한 뒤에, 각 state에 agent가 있을 확률 분포라고도 말할 수 있을 것이다.

\begin{bmatrix}\Pi^{(n)}_1&\Pi^{(n)}_2&\Pi^{(n)}_3\end{bmatrix} = \begin{bmatrix}\Pi^{(n-1)}_1&\Pi^{(n-1)}_2&\Pi^{(n-1)}_3\end{bmatrix}P = \begin{bmatrix}\Pi^{(0)}_1&\Pi^{(0)}_2&\Pi^{(0)}_3\end{bmatrix}P^{n}

N-step Transition Probability

i-state 부터 j-state까지 N steps 동안 가야한다고 했을 때를 생각해보자. 1 step 부터 (N-1) step 까지 어떤 state로든 다 갈 수 있으나, 마지막 j-state의 바로 전 step은 무조건 k-state에서 j-state로 향해야한다.

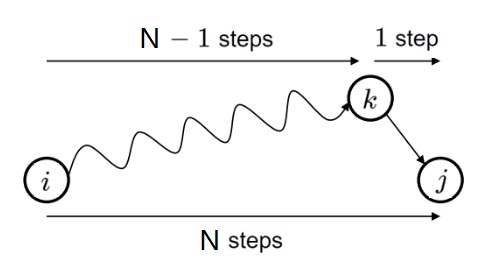
[이미지 출처: iAI postech]

n-step transition probability를 Markov chain process를 사용해 다음과 같이 쓸 수 있을 것이다.

P_{ij}(n) = \sum_{k=1}^N {P_{ik}(n-1)P_{kj}(1)}

where \;\; {\begin{cases} \;p_{ij}(n) = P(x_n = j | x_0 = i)\\ \;p_{ij}(1) = p_{ij} = P(x_1 = j | x_0 = i) \end{cases}}

Staitionary Distribution

Chapman-Kolmogorov Equation을 통해서 행렬곱으로 표현하게 되면, 1 step 부터 (N-1) step 동안 i-state 부터 j-state의 직전 state인 k-state까지 갈 수 있는 확률과 무조건 k-state에서 j-state로 가는 마지막 step의 두 확률을 곱한 식으로도 표현할 수 있다.

P_{ij}(n) = {\Pi}P^{(n-1)}P

여기서 n을 무한대로 보냈을 때, 즉 충분한 시간이 흐르고나서, $\,p_{ij}(n)$ 는 어떠한 $\pi_j$ 로 saturation(수렴) 할까? 다시 말해서 j에 있을 확률은 어떻게 될까?

\pi_j = \sum_{k=1}^N{\pi_kP_{kj}}

\sum_{j}{\pi_j} = 1

\pi = {\pi}P

n을 무한대로 보내게 되면 n-1에 있을 때의 $\pi$ 와 n에 있을 때의 $\pi$ 가 거의 동일해질 것이다. $\pi$ 가 의미하는 바는 steady state(시간이 충분히 지나고)에서 이 process를 따르는 agent가 각 state에 있을 확률을 말하는 것이다.

궁극적으로 알고 싶은 건, state transition matrix를 따를 때에 시간이 무한대로 지나가가고, 어떤 episode에 종착하게 될 텐데 그때 각 state에 agent가 있을 확률을 종합해서 결론을 내려야한다.

Reference

(1) 03 Markov chain (마르코프 체인), iAI LAB, POSTECH, 2022. 3. 1.
좋은 강의 영상을 올려주신 iAI POSTECH에 감사드립니다.

Gahyeon Kim

이제부터 하려고요,,,,velog

다음 포스트

본 딥러닝도 다시보자 01: Markov Chain Process