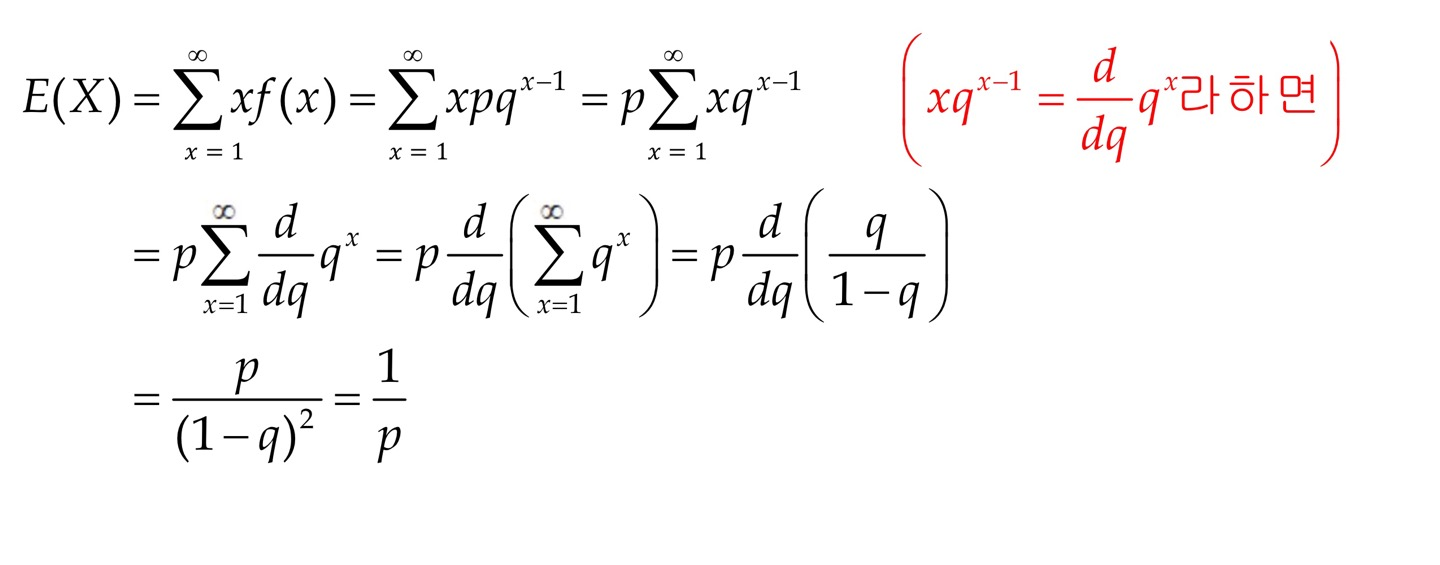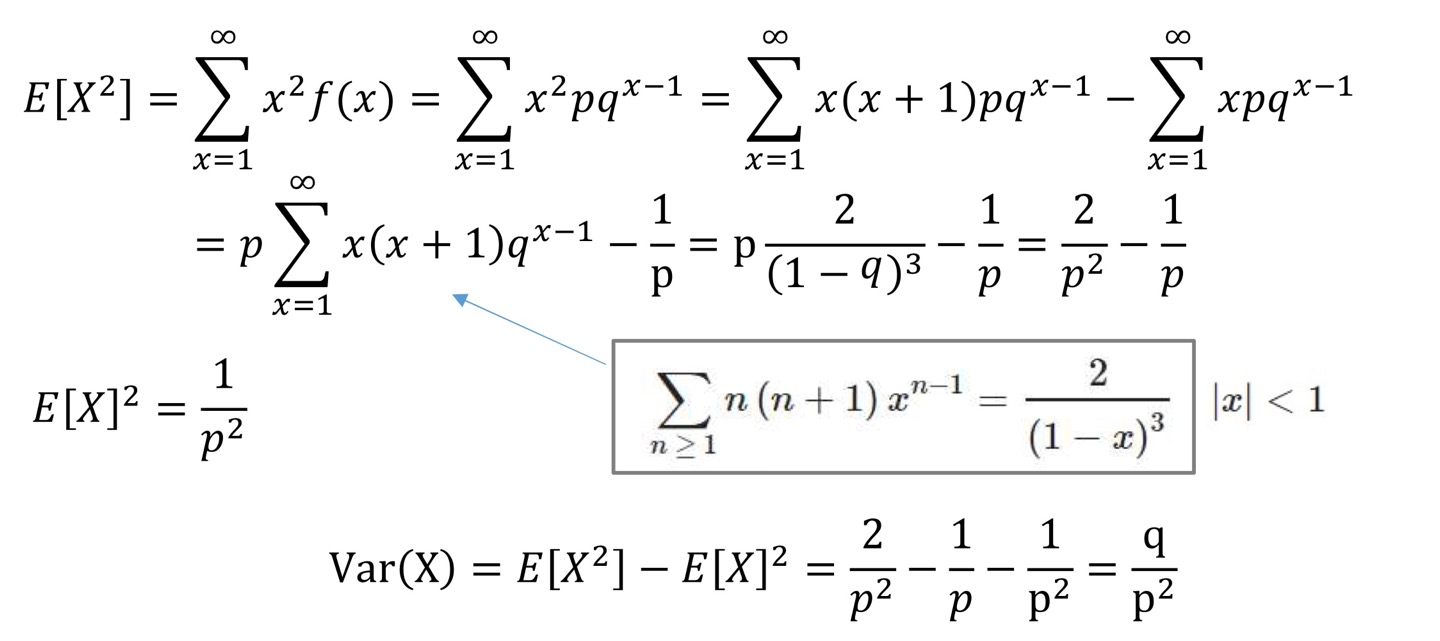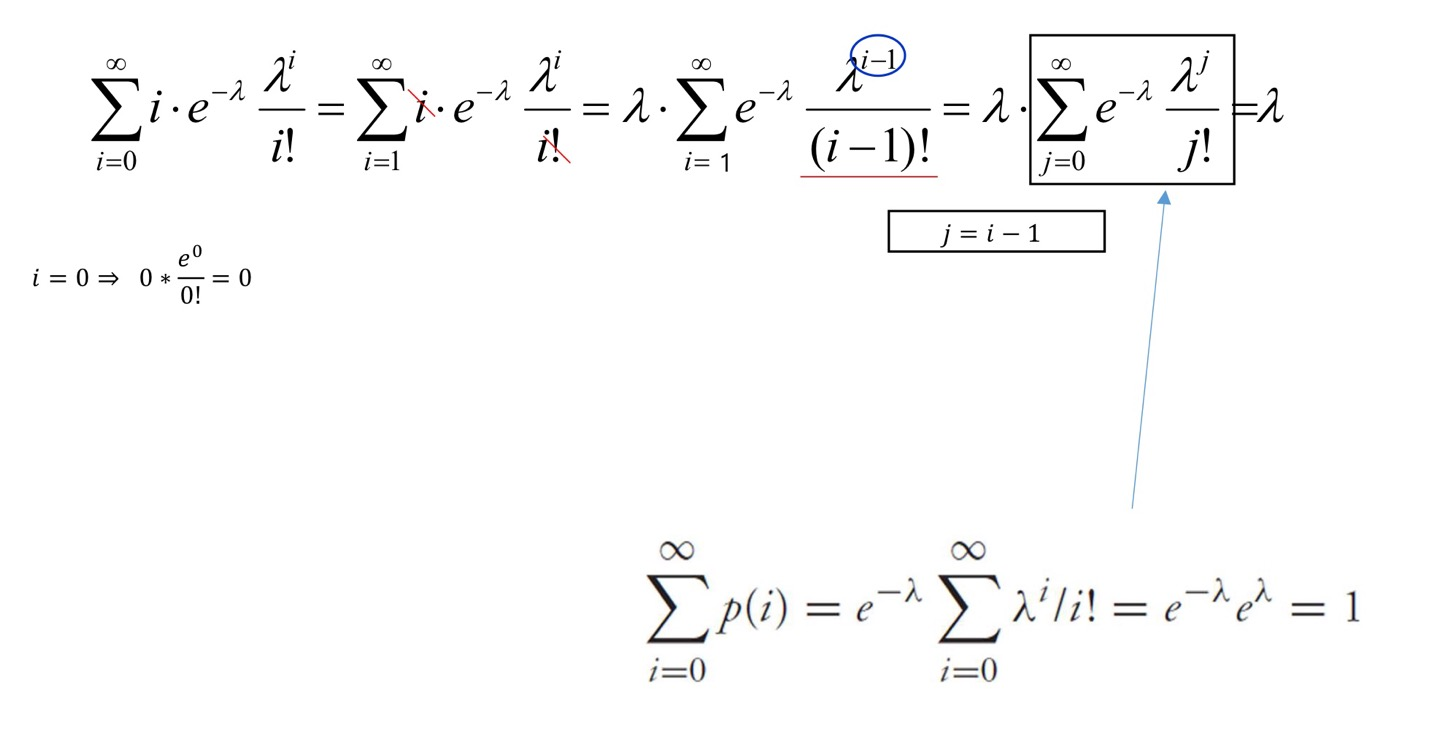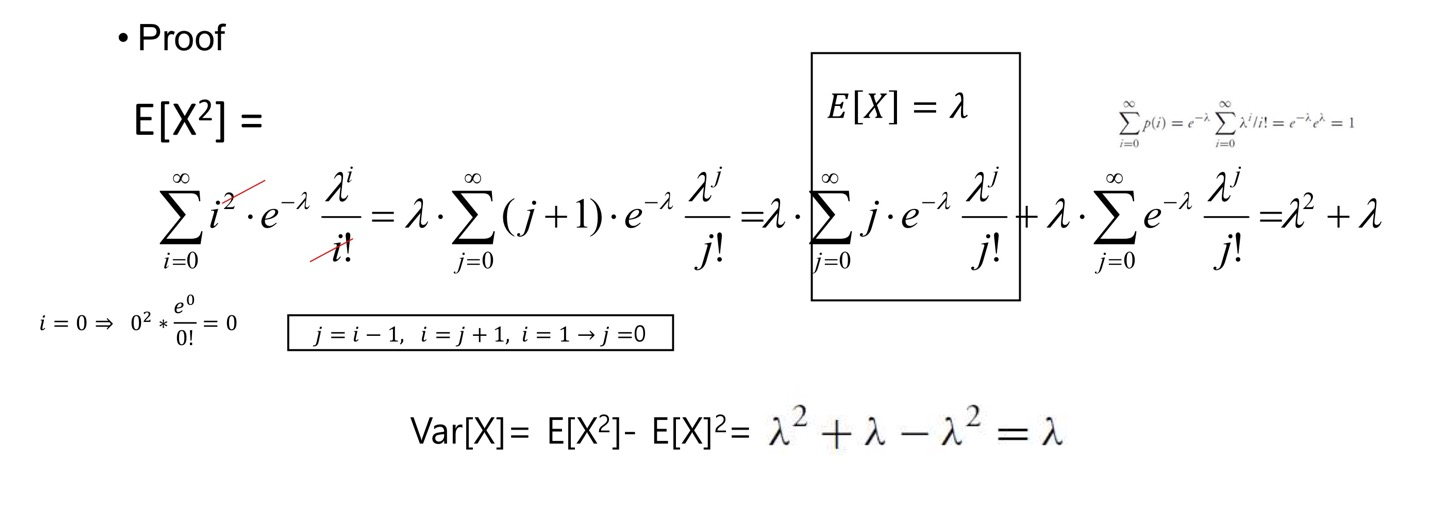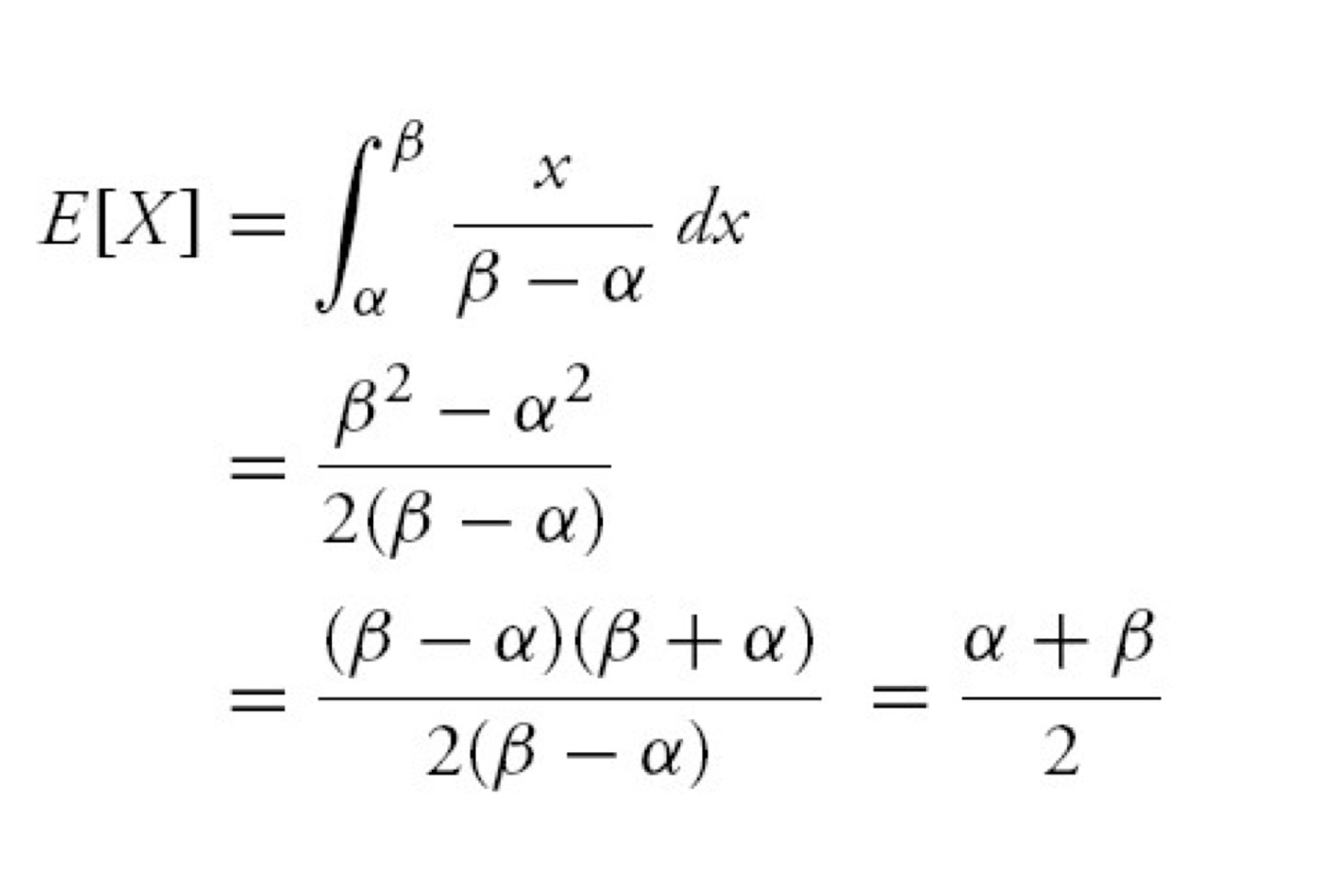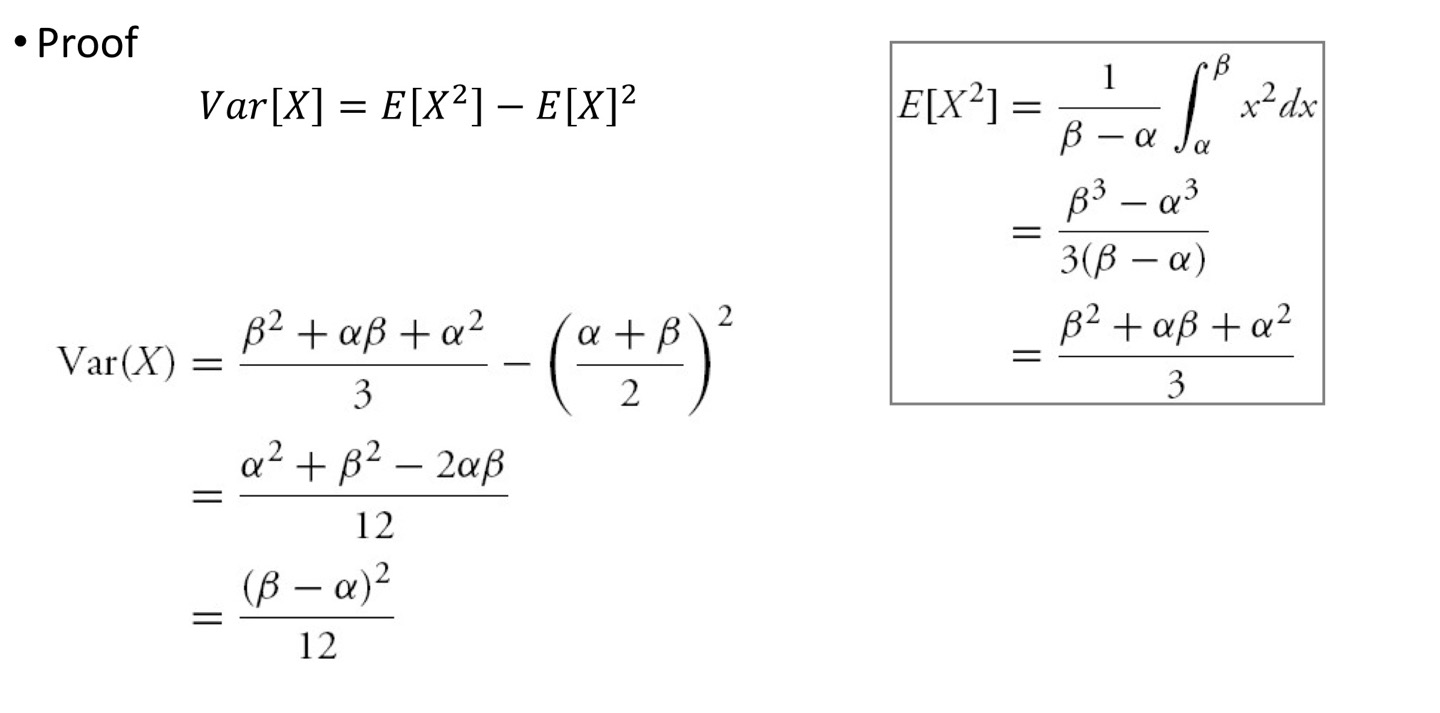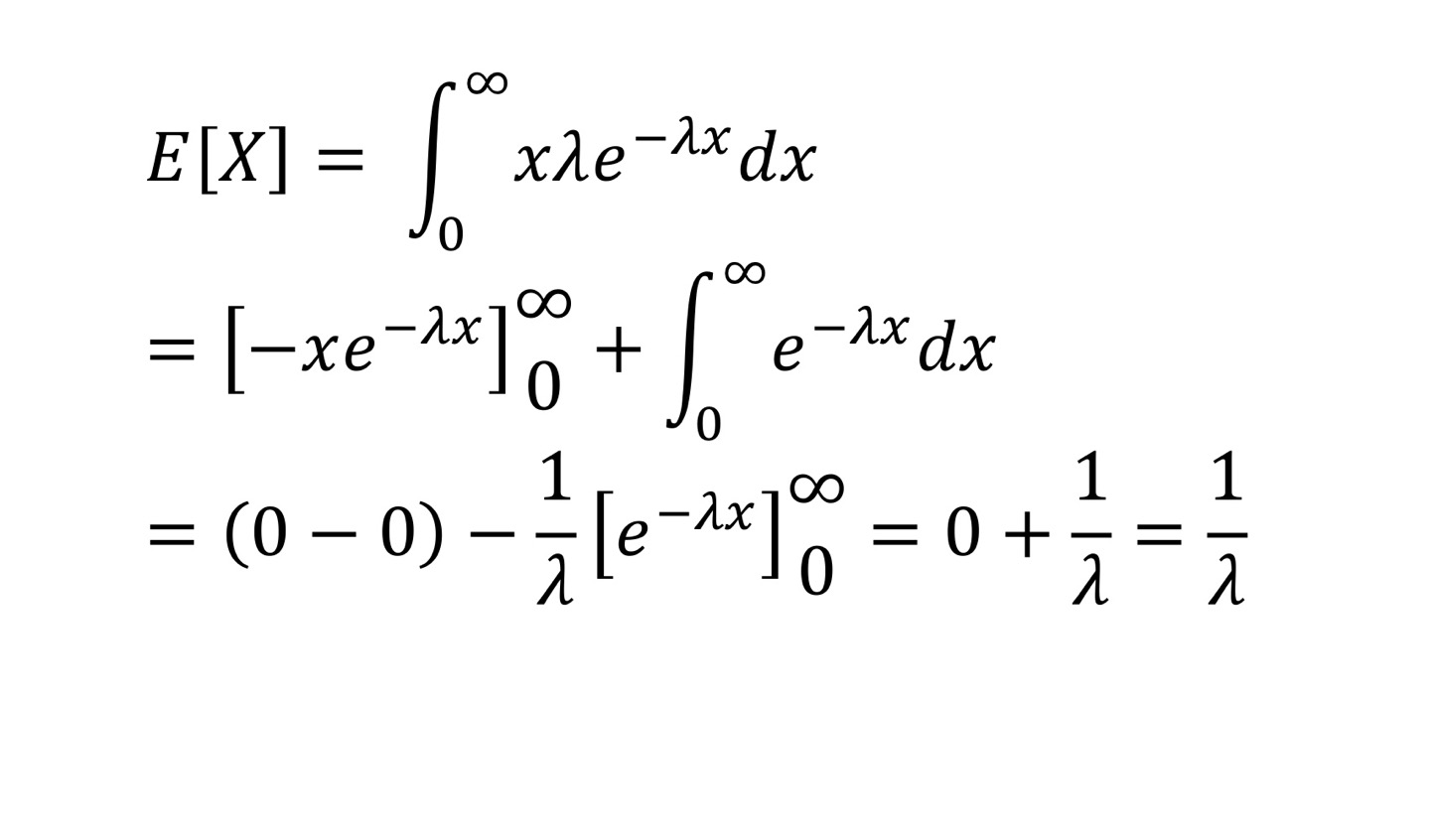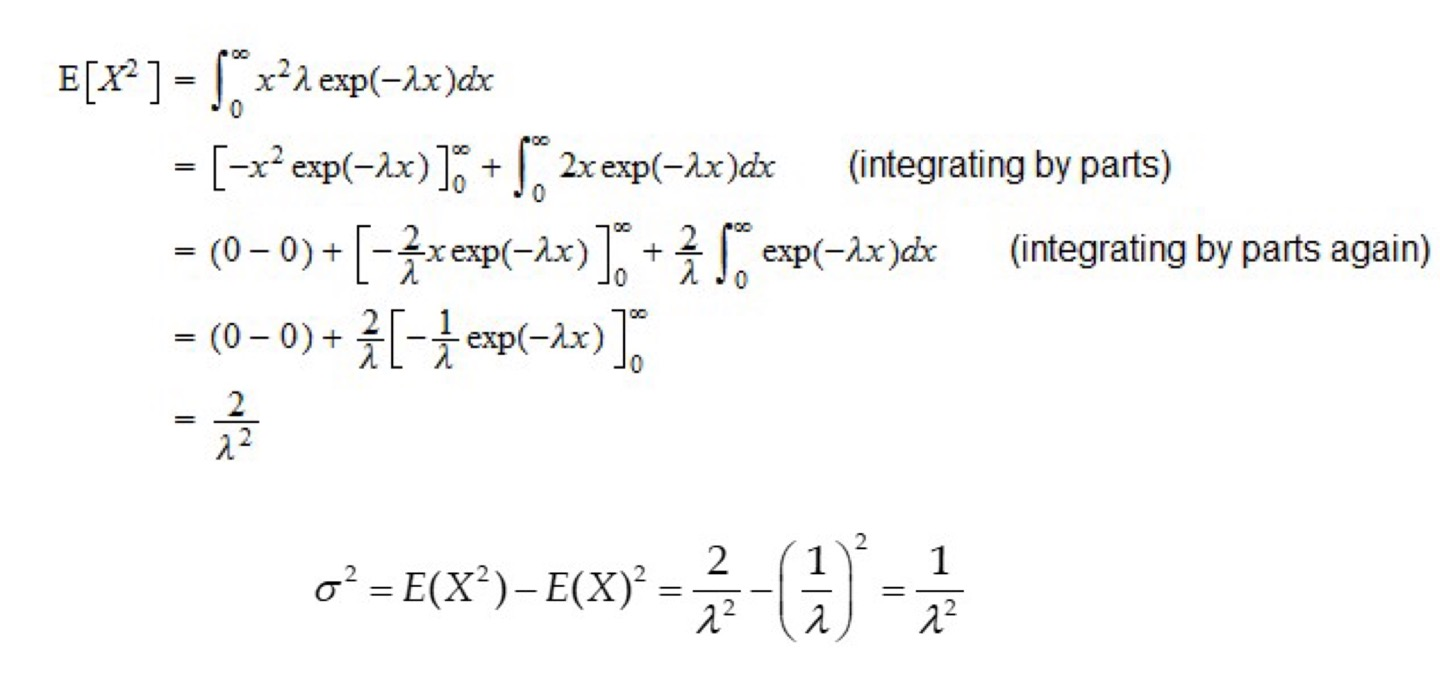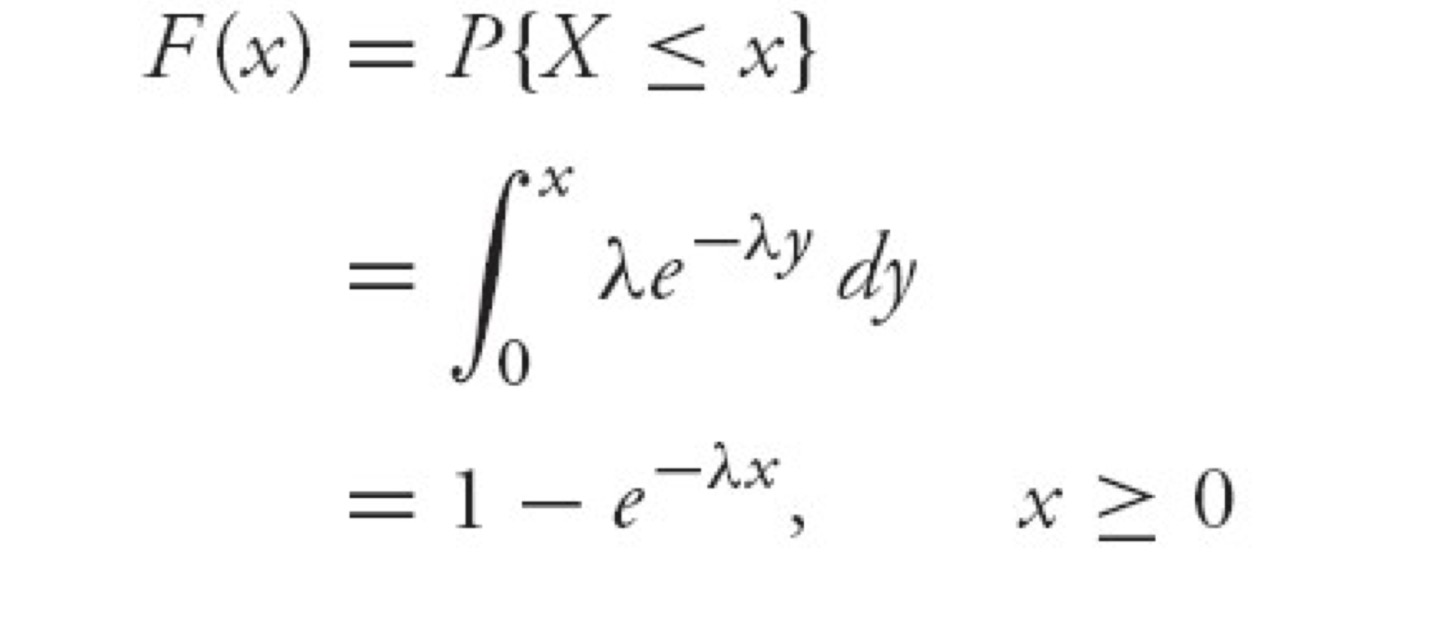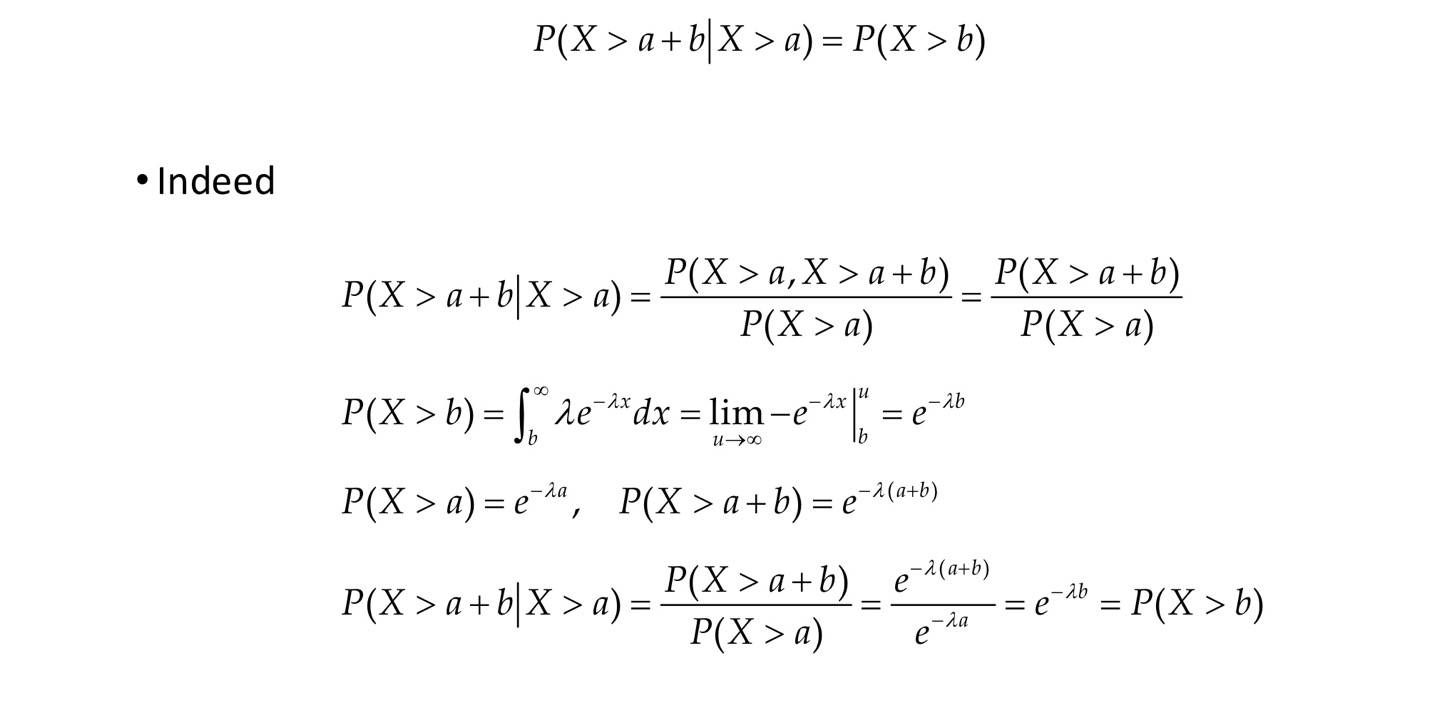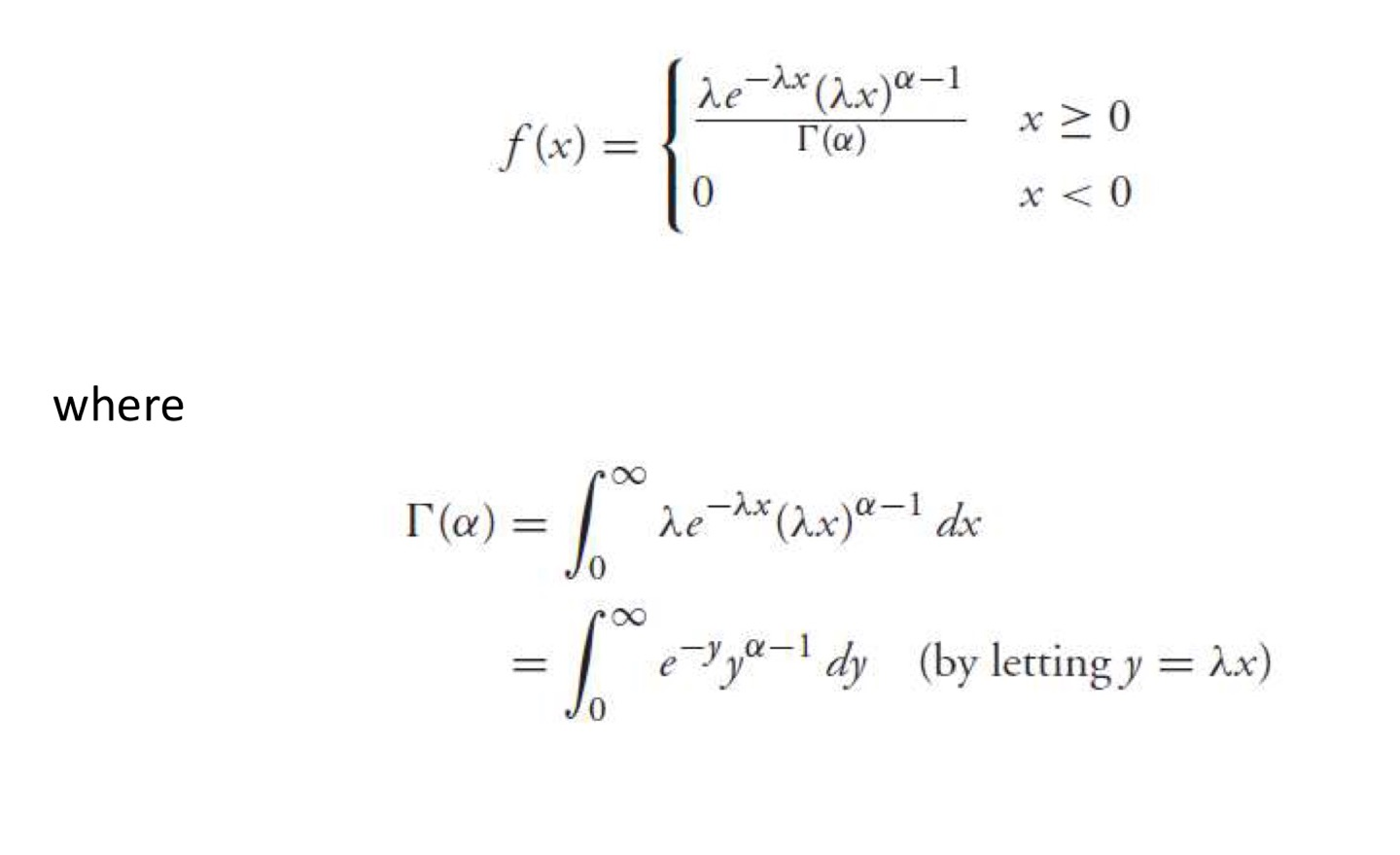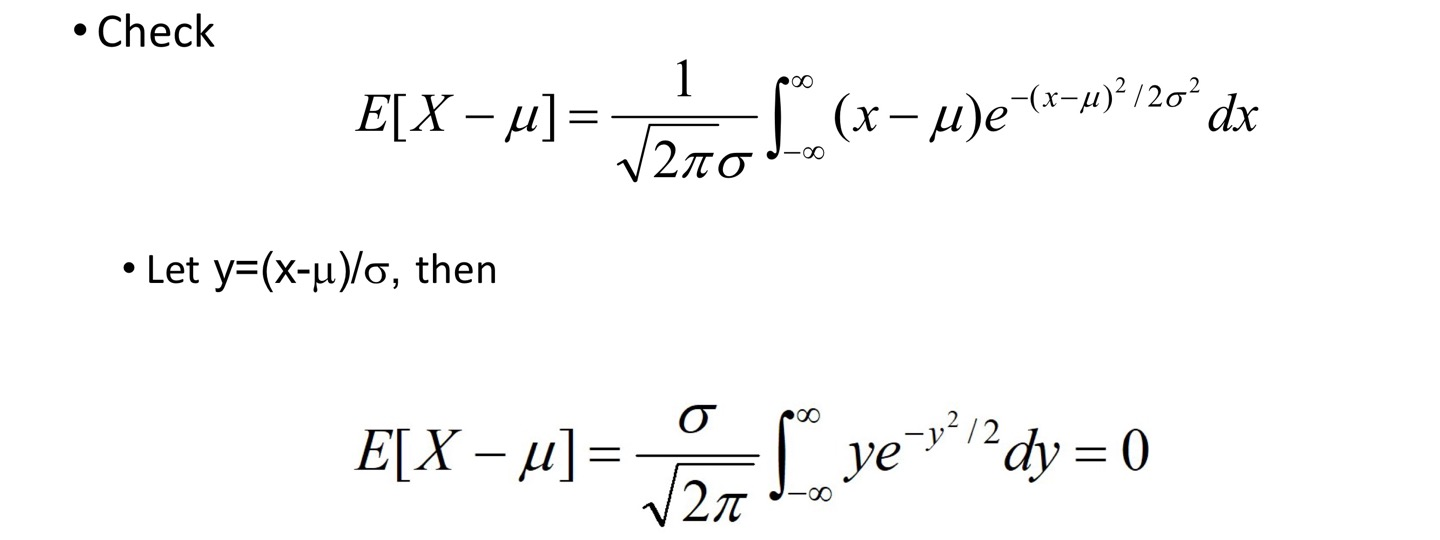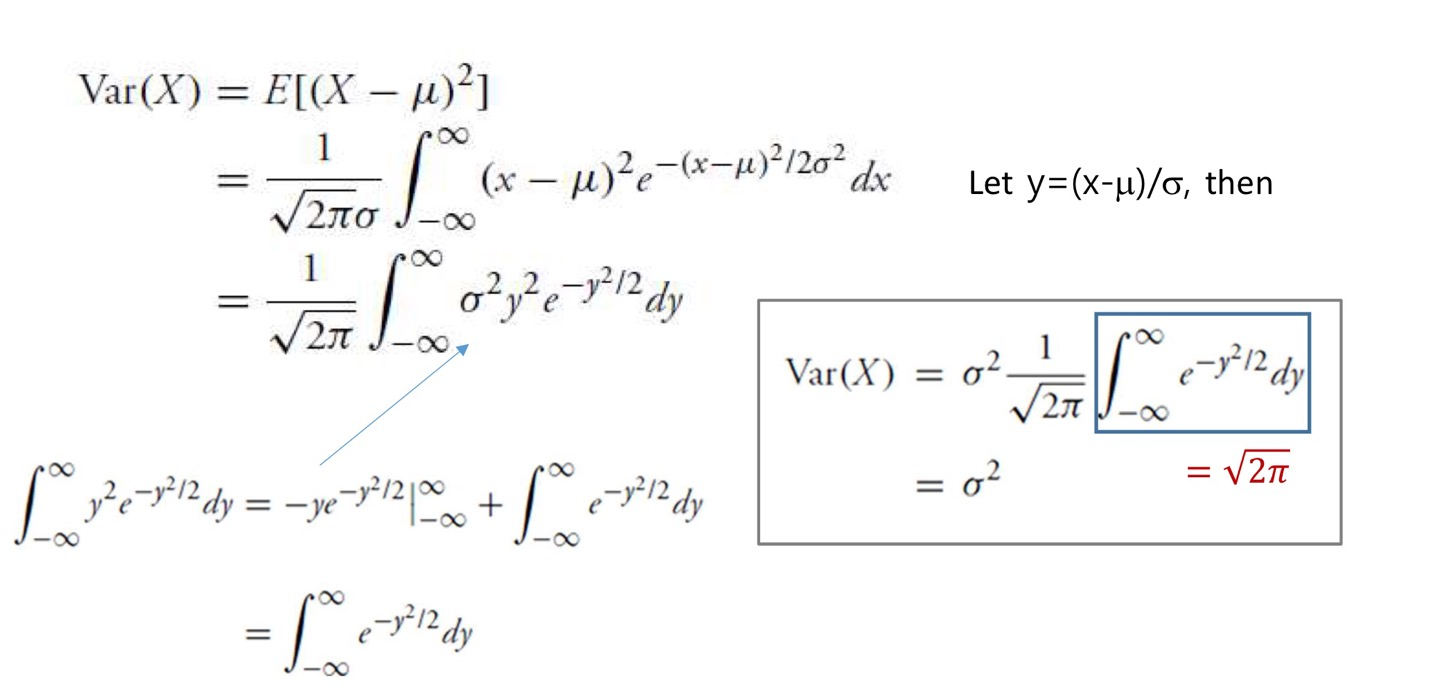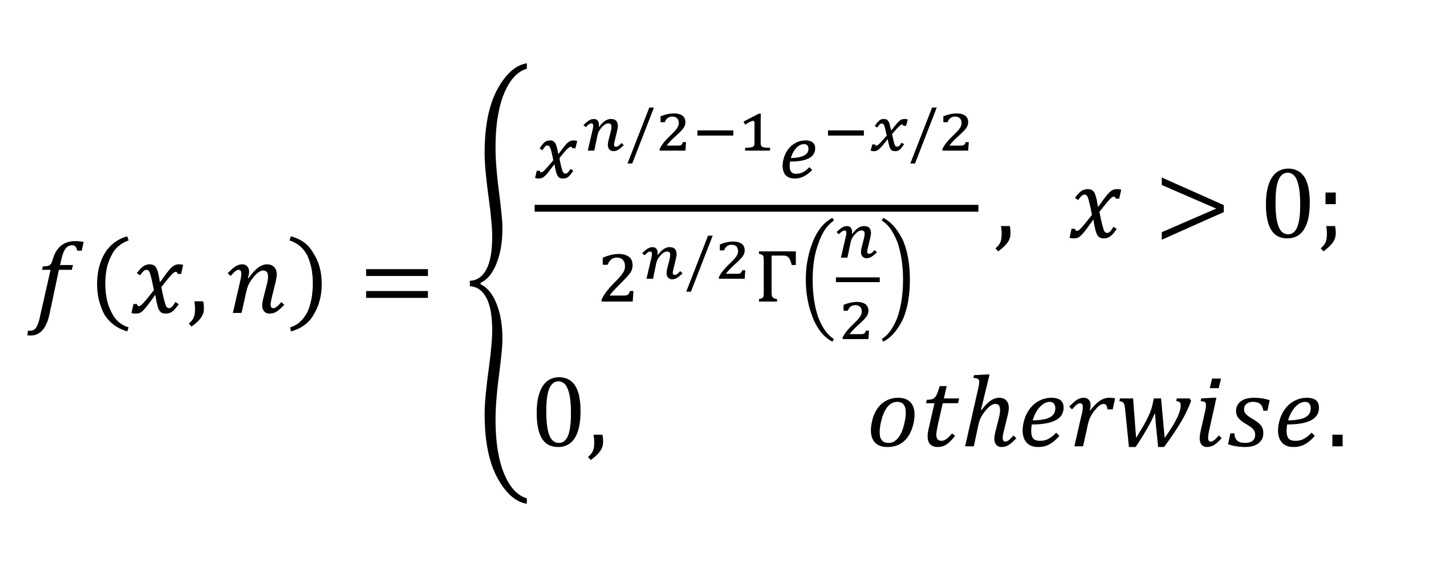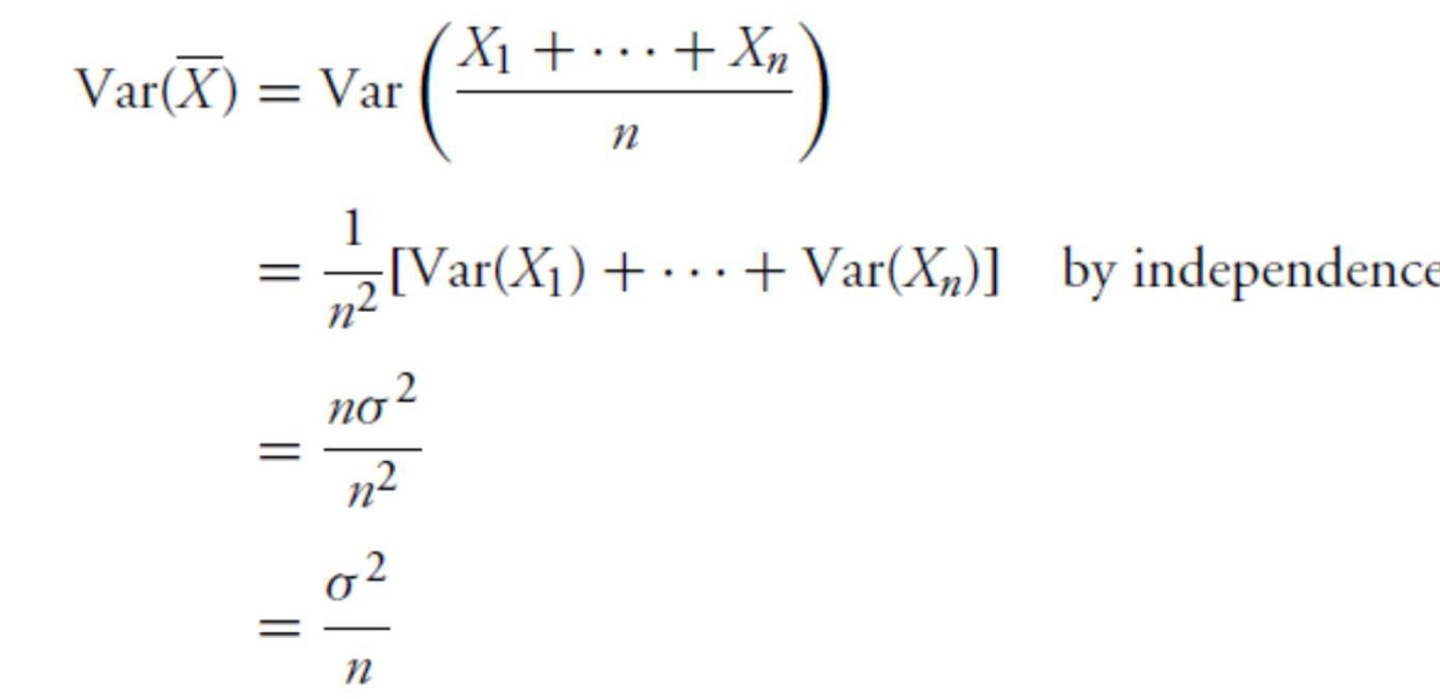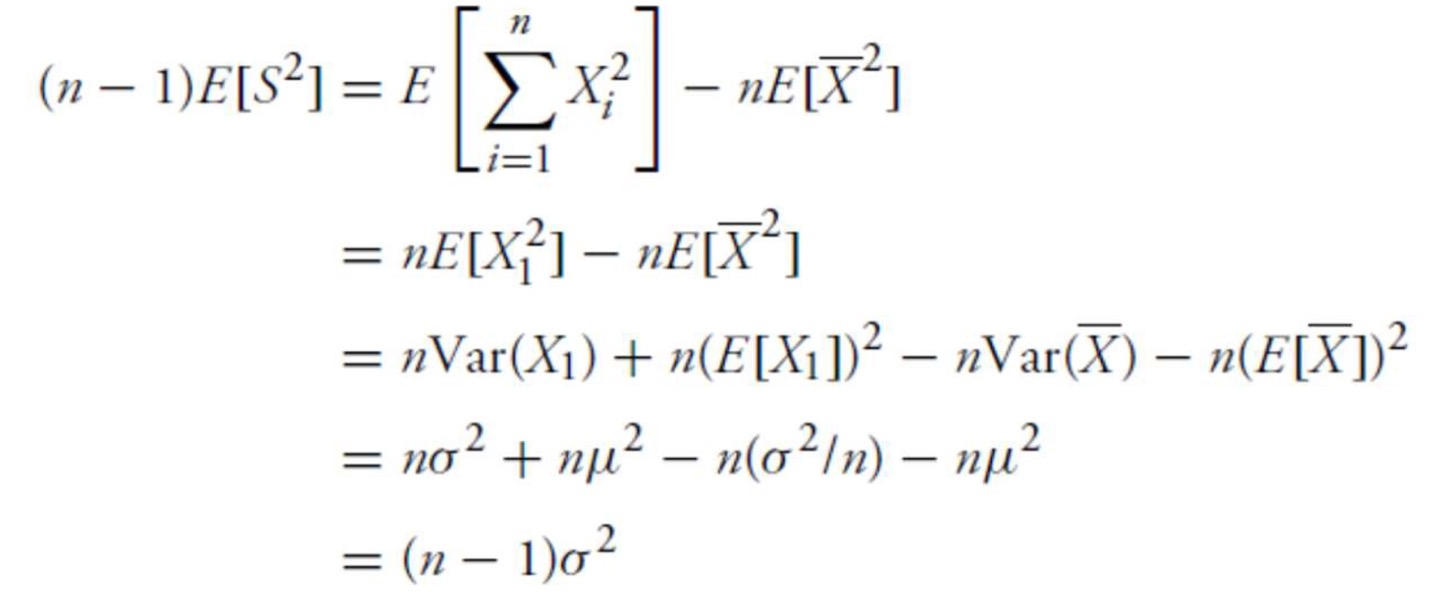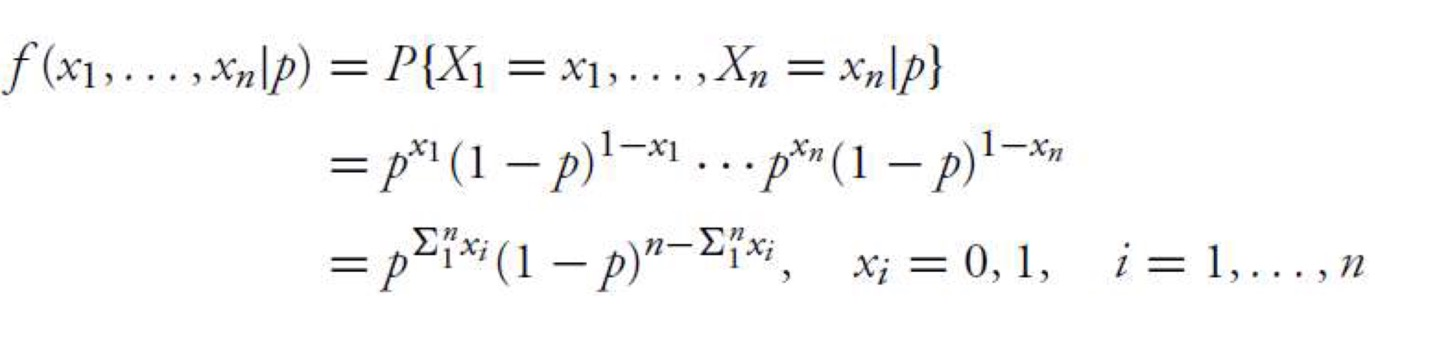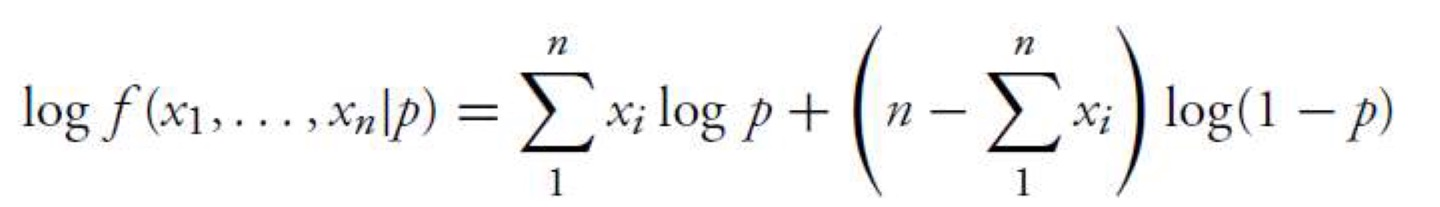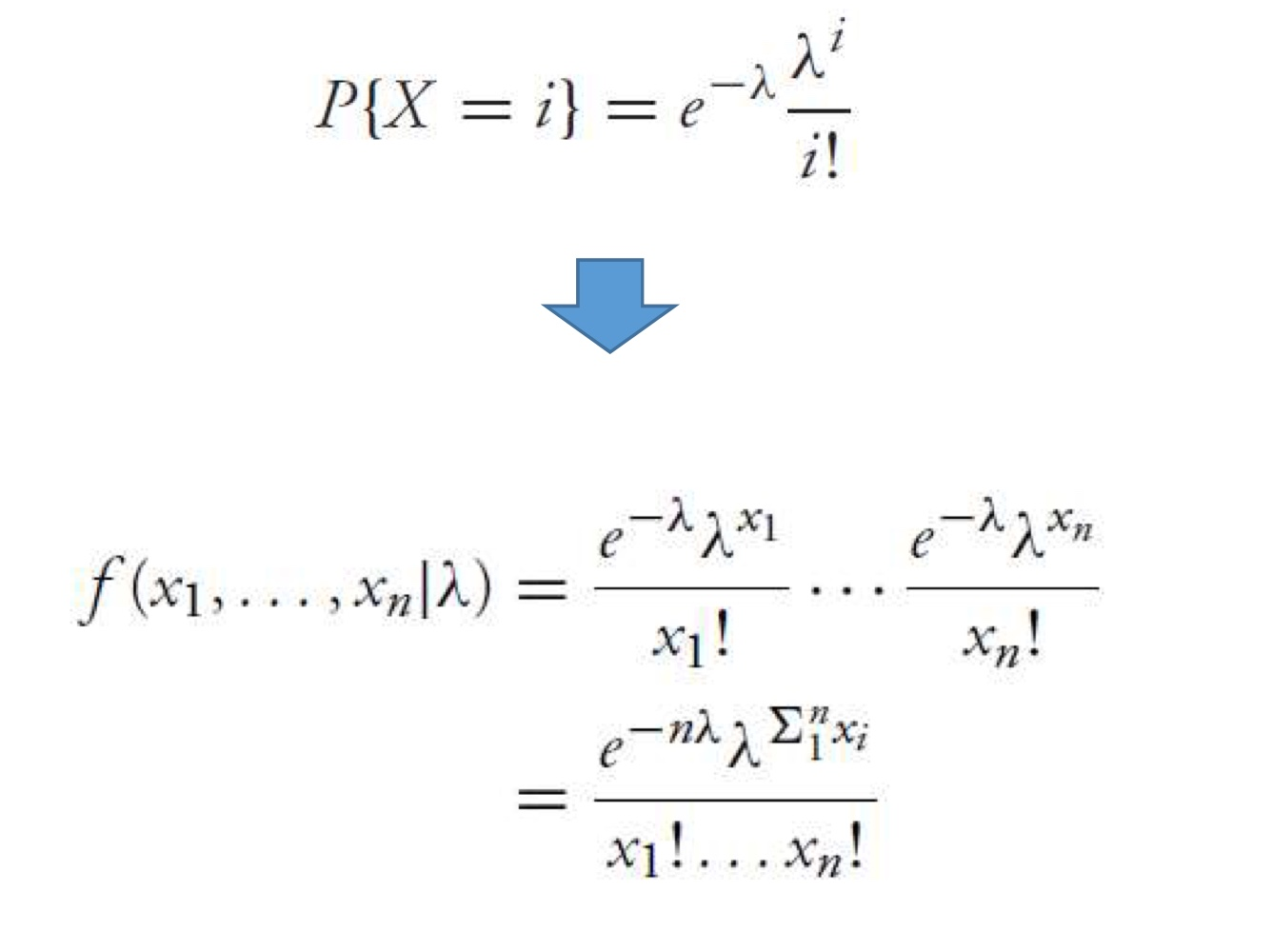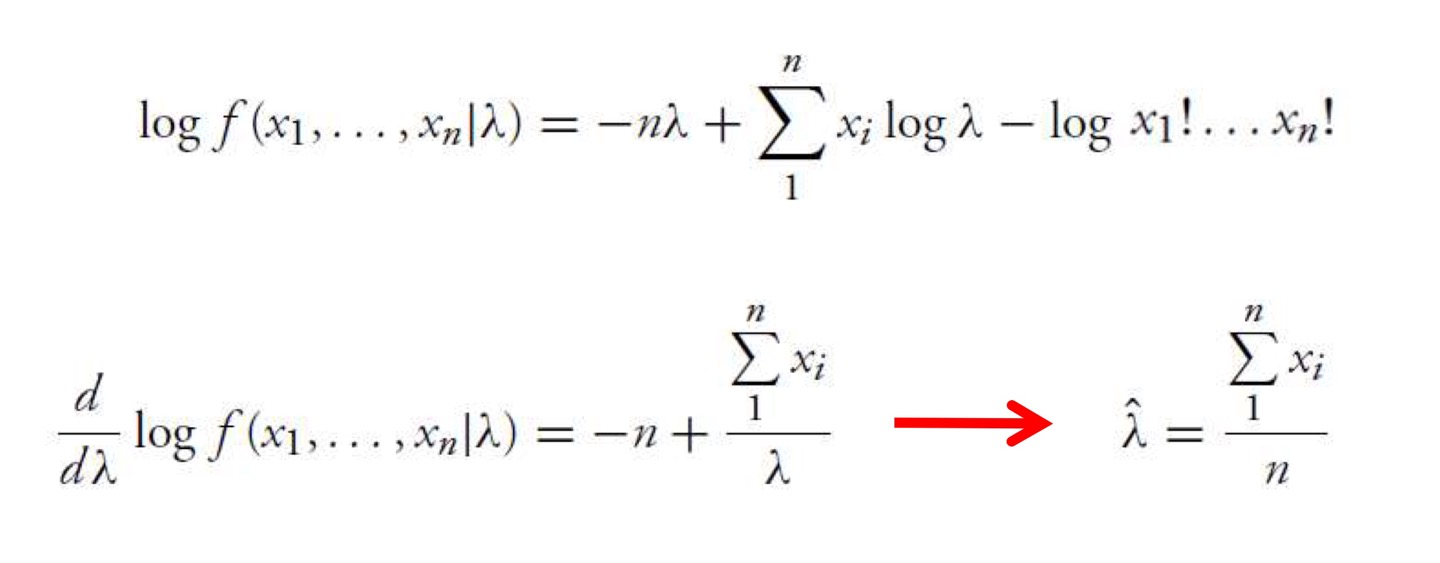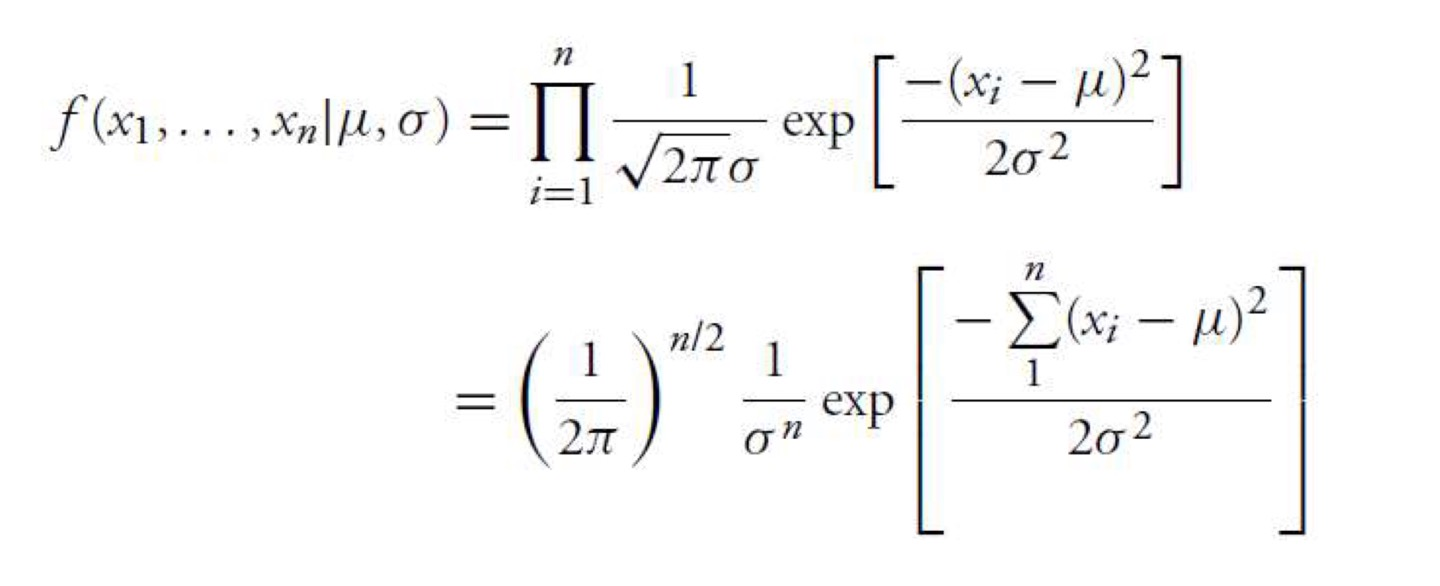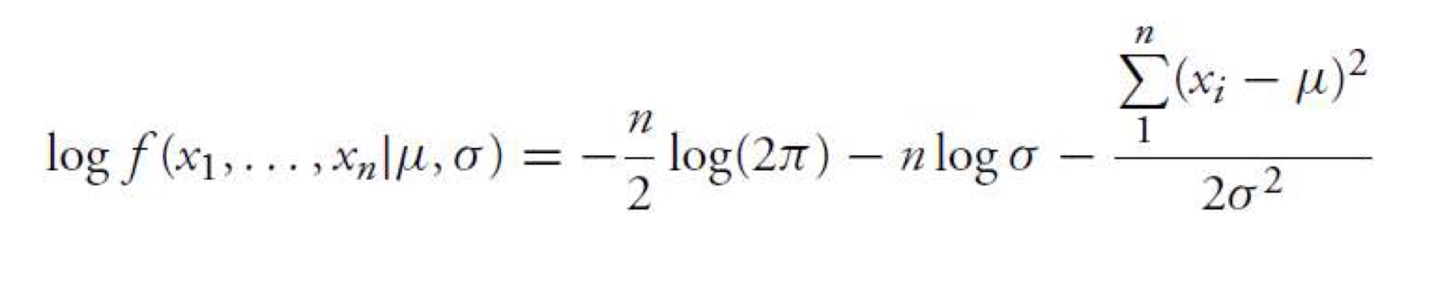균등분포
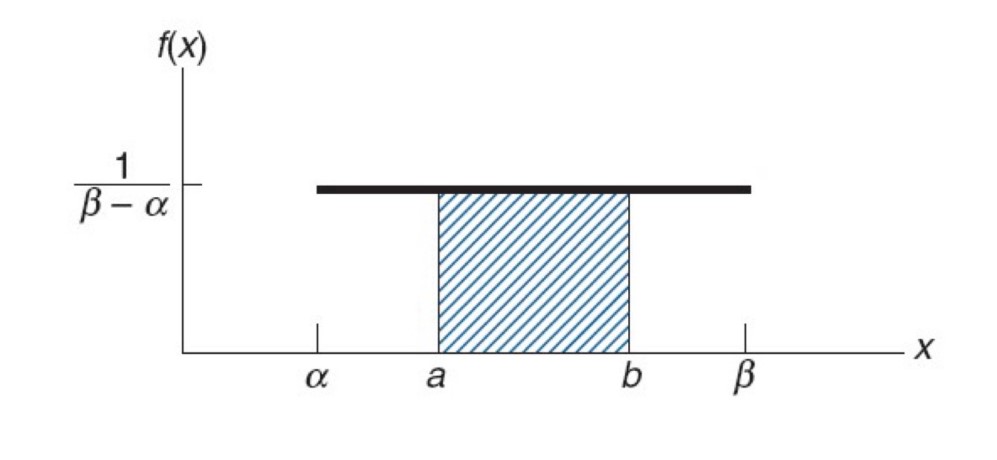
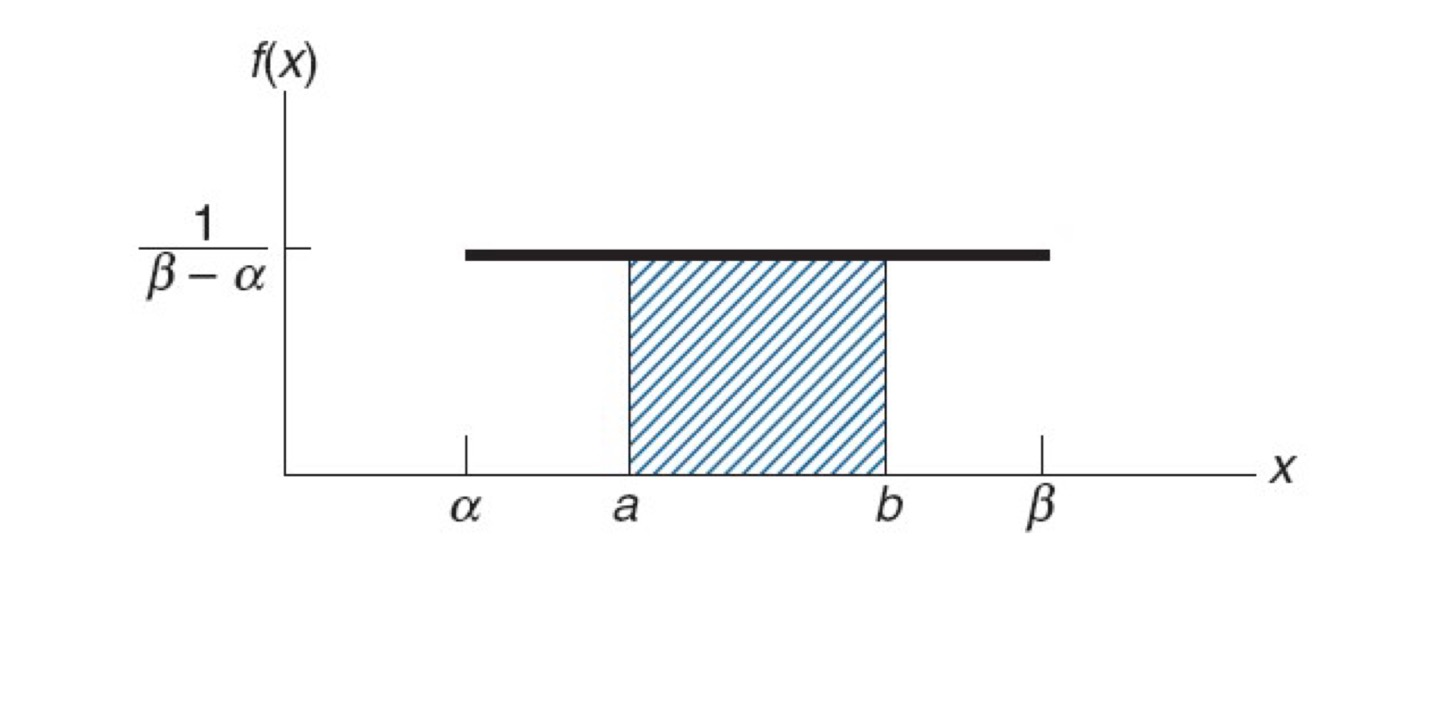
모든 확률이 같음m e a n = E ( X ) = n + 1 2 mean =E(X)= \frac{n+1} {2} m e a n = E ( X ) = 2 n + 1 V a r i a n c e = n 2 − 1 12 Variance=\frac{n^2-1} {12} V a r i a n c e = 1 2 n 2 − 1
Bernoulli RV
베르누이 확률분포
Binomial RV
이산 확률 분포
베르누이 시행이 여러번 있는 것 (독립)
사건이 시행될 횟수를 X , 확률분포로 보고 사용
X ∼ B ( n , p ) X\sim B(n,p) X ∼ B ( n , p )
Probability mass function
P { X = i } = ( n i ) p i ( 1 − p ) n − i P\left\{ X=i \right\}= {n \choose i}p^i(1-p)^{n-i} P { X = i } = ( i n ) p i ( 1 − p ) n − i
Expectation
E [ X ] = ∑ i = 1 n E [ X i ] = n p E[X]=\sum_{i=1}^n E[X_i]=np E [ X ] = i = 1 ∑ n E [ X i ] = n p
Variance
V a r ( X ) = ∑ i = 1 n V a r ( X i ) = n p ( 1 − p ) Var(X)=\sum_{i=1}^n Var(X_i)=np(1-p) V a r ( X ) = i = 1 ∑ n V a r ( X i ) = n p ( 1 − p )
Multinomial RV
다항 분포
f ( x ) = { 1 → 3 , 주사위가 1 이 나온 횟수 2 ∼ 4 → 5 , 주사위가 2 ∼ 4 가 나온 횟수 5 → 1 , 주사위가 5 가 나온 횟수 6 → 1 , 주사위가 6 이 나온 횟수 f(x)= \begin{cases} 1\rightarrow3, & { 주사위가\ 1이 \ 나온 \ 횟수} \\ 2\sim4\rightarrow5, & { 주사위가\ 2\sim4가 \ 나온 \ 횟수} \\ 5\rightarrow1, & { 주사위가\ 5가 \ 나온 \ 횟수} \\ 6\rightarrow1, & { 주사위가\ 6이 \ 나온 \ 횟수} \\ \end{cases} f ( x ) = ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ 1 → 3 , 2 ∼ 4 → 5 , 5 → 1 , 6 → 1 , 주 사 위 가 1 이 나 온 횟 수 주 사 위 가 2 ∼ 4 가 나 온 횟 수 주 사 위 가 5 가 나 온 횟 수 주 사 위 가 6 이 나 온 횟 수
Probabillity mass functionf ( x 1 , . . . , x k ; p 1 . . . , p k ) = P r ( X 1 = x 1 a n d . . . a n d X k = x k ) = { n ! x 1 ! . . . x k ! p 1 x 1 × p k x k 0 f(x_1,...,x_k;p_1...,p_k)=Pr(X_1=x_1\ and \ ...\ and \ X_k=x_k)= \begin{cases} \frac {n!} {x_1!...x_k!}p^{x_1}_1\times p^{x_k}_k \\ 0 \end{cases} f ( x 1 , . . . , x k ; p 1 . . . , p k ) = P r ( X 1 = x 1 a n d . . . a n d X k = x k ) = { x 1 ! . . . x k ! n ! p 1 x 1 × p k x k 0
Property
Mean
E ( X i ) = n p i E(X_i)=np_i E ( X i ) = n p i
Variance
V a r ( X i ) = n p i ( 1 − p i ) Var(X_i)=np_i(1-p_i) V a r ( X i ) = n p i ( 1 − p i )
Covariance
C o v ( X i , X j ) = − n p i p j Cov(X_i,X_j)=-np_ip_j C o v ( X i , X j ) = − n p i p j
Geometric RV
기하 분포
X= number of Bernoulli trials (p) to get "firtst success "
Probability mass functionS u c e s s = p Sucess = p S u c e s s = p F a i l u r e = 1 − p Failure=1-p F a i l u r e = 1 − p P r ( X = k ) = ( 1 − p ) k − 1 p f o r k = 1 , 2 , 3... Pr(X=k)=(1-p)^{k-1}p\qquad for \ k=1,2,3... P r ( X = k ) = ( 1 − p ) k − 1 p f o r k = 1 , 2 , 3 . . .
Property
Mean
μ = 1 p ( p > 0 ) \mu=\frac {1} {p} \qquad (p>0) μ = p 1 ( p > 0 )
proof
Variance
σ 2 = q p 2 ( q = 1 − p ) \sigma^2=\frac {q} {p^2} \qquad (q=1-p) σ 2 = p 2 q ( q = 1 − p )
proof
Memoryless property
P ( X > n + m ∣ X > n ) = P ( X > m ) P(X>n+m|X>n)=P(X>m) P ( X > n + m ∣ X > n ) = P ( X > m )
X>n+m : n이 경과 된 상태에서 m이라는 시간이 더 지났다.
if n=5, m=3 이면 5년이 지난 상태에서 3년이 더 지났을 때 고장이 날 확률은 3년 이후에 처음 고장이 발생 될 확률과 같다.
앞의 5년을 잊어버린다. = memoryless
Poisson RV
푸아송 분포
X ∼ P o i s ( λ ) ( λ = n p ) X\sim Pois(\lambda)\qquad (\lambda=np) X ∼ P o i s ( λ ) ( λ = n p )
Probability mass functionP { X = x } = e − λ λ x x ! P\left\{ X=x \right\}=e^{-\lambda}\frac{\lambda^x} {x!} P { X = x } = e − λ x ! λ x
Property
VarianceV a r [ X ] = λ Var[X]=\lambda V a r [ X ] = λ
균일분포
Exponential RV
지수분포 (푸아송 분포에서 유도)
Memoryless Property
Gamma RV
감마분포 (지수분포의 일반화된 형태)
Normal Distribution
정규분포 (연속확률분포의 한 종류)
X ∼ N ( μ , σ 2 ) X \sim \mathcal{N}(\mu,\sigma^2) X ∼ N ( μ , σ 2 )
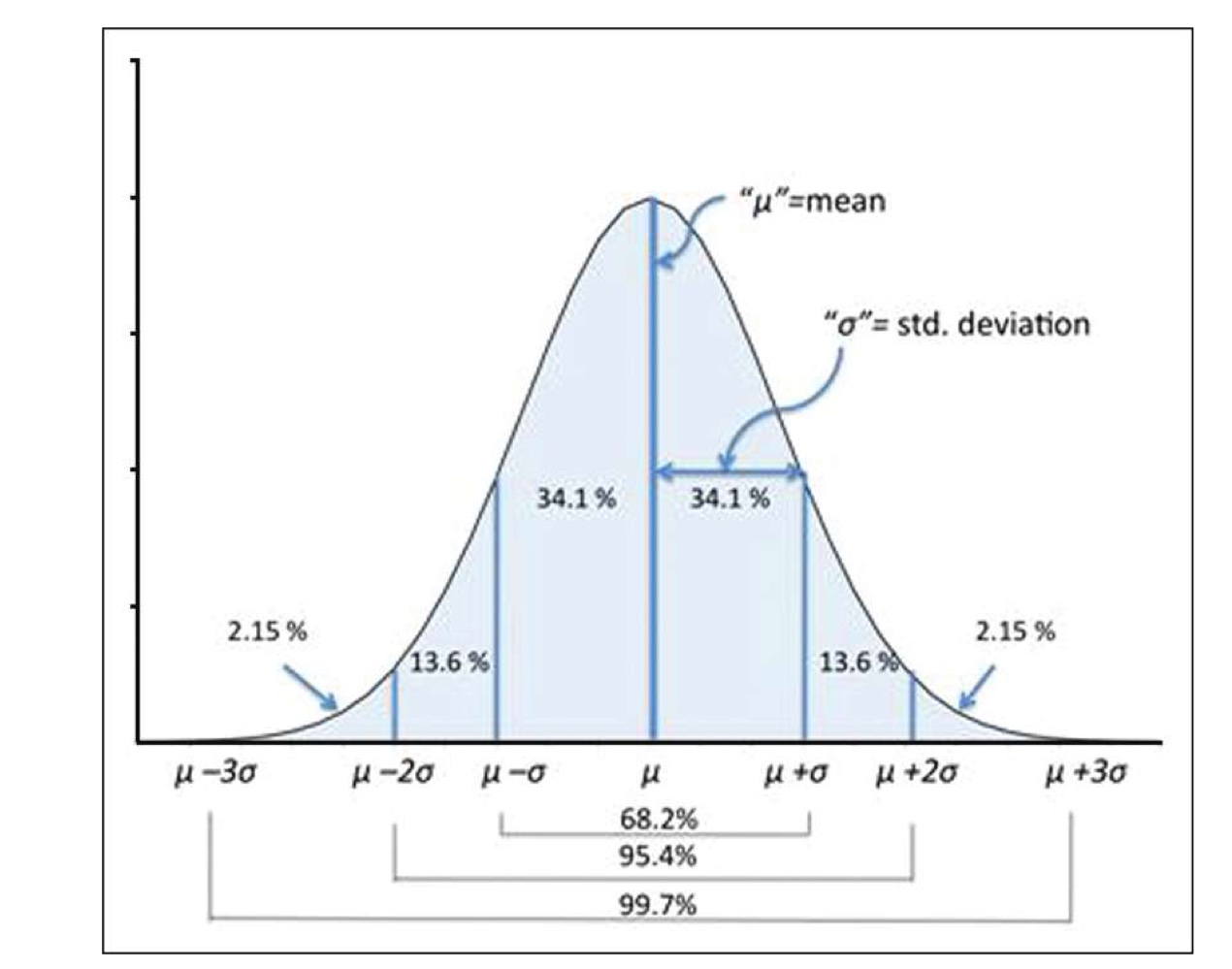
그래프의 면적 = 확률
좌우대칭 (뮤 기준)
Probability density function
f ( x ) = 1 2 π σ e − ( x − μ ) 2 / 2 σ 2 , − ∞ < x < ∞ f(x)=\frac {1} {\sqrt{2\pi}\sigma}e^{-(x-\mu)^2/2\sigma^2},\qquad -\infin <x<\infin f ( x ) = 2 π σ 1 e − ( x − μ ) 2 / 2 σ 2 , − ∞ < x < ∞
Maximum value :
i f Y ∼ N ( 5 , 2 2 ) if\ \ \ \ Y\sim\mathcal{N}(5,2^2) i f Y ∼ N ( 5 , 2 2 ) X ∼ N ( 2 , 1 2 ) → P ( 1 ≤ x ≤ 3 ) = P ( 2 − 1 ( μ − σ ) ) ≤ X ≤ 2 + 1 ( μ + σ ) ) X\sim\mathcal{N}(2,1^2) \rightarrow P(1\le x\le 3)=P(2-1_{(\mu-\sigma)}) \le X\le 2+1_{(\mu+\sigma)}) X ∼ N ( 2 , 1 2 ) → P ( 1 ≤ x ≤ 3 ) = P ( 2 − 1 ( μ − σ ) ) ≤ X ≤ 2 + 1 ( μ + σ ) ) s o Y ∼ N ( 5 , 2 2 ) → P ( 5 − 2 ( μ − σ ) ≤ Y ≤ 5 + 2 ( μ + σ ) ) = P ( 3 ≤ Y ≤ 7 ) so\ \ Y\sim \mathcal{N}(5,2^2)\rightarrow P(5-2_{(\mu-\sigma)}\le Y \le 5+2_{(\mu+\sigma)})=P(3\le Y\le7) s o Y ∼ N ( 5 , 2 2 ) → P ( 5 − 2 ( μ − σ ) ≤ Y ≤ 5 + 2 ( μ + σ ) ) = P ( 3 ≤ Y ≤ 7 )
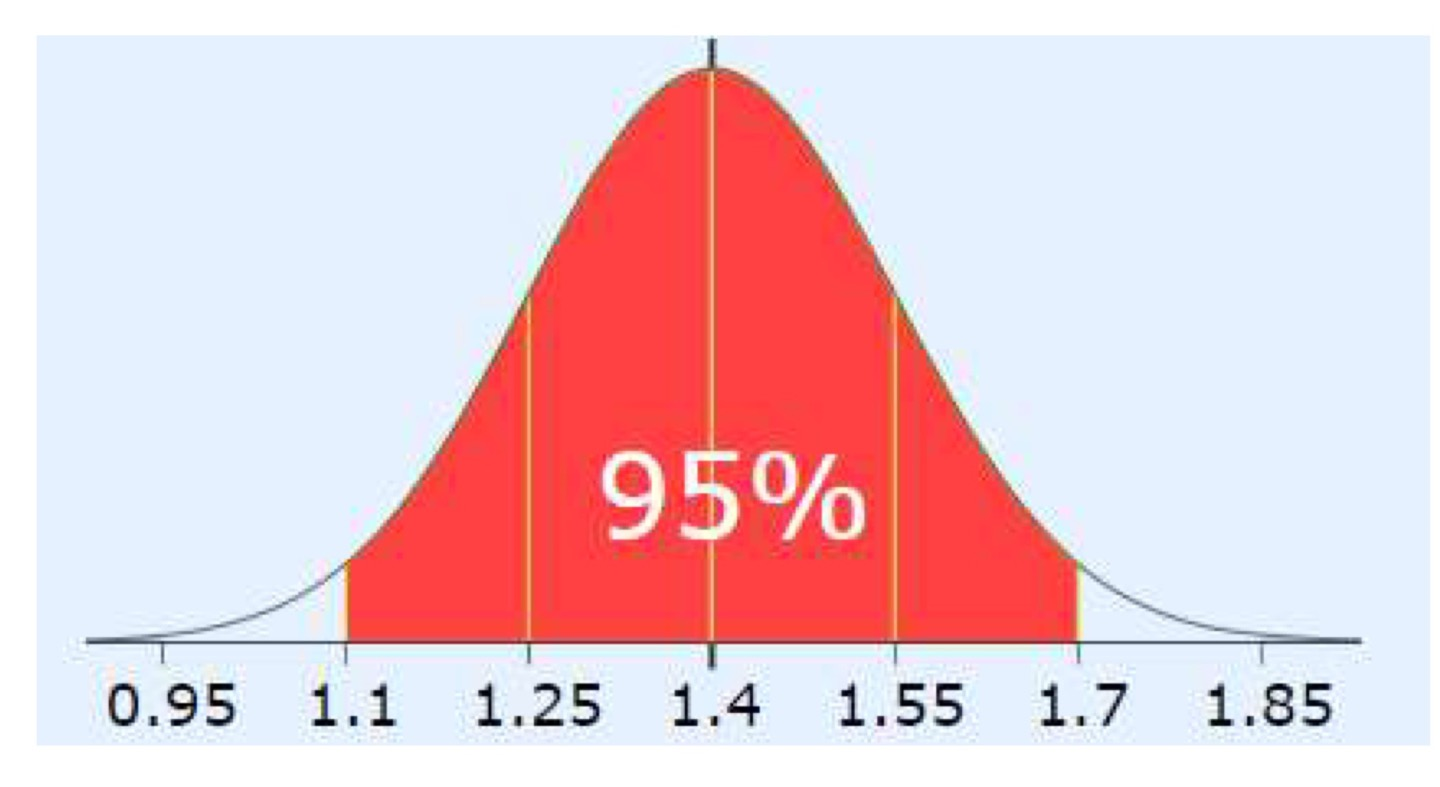
Mean = 1.4
SD(표준편차)=(1.7 - 1.1) / 4 = 0.15 (since 95% is 2 SD either side, total 4 SD)
Property
V a r ( X ) = σ 2 Var(X)=\sigma^2 V a r ( X ) = σ 2
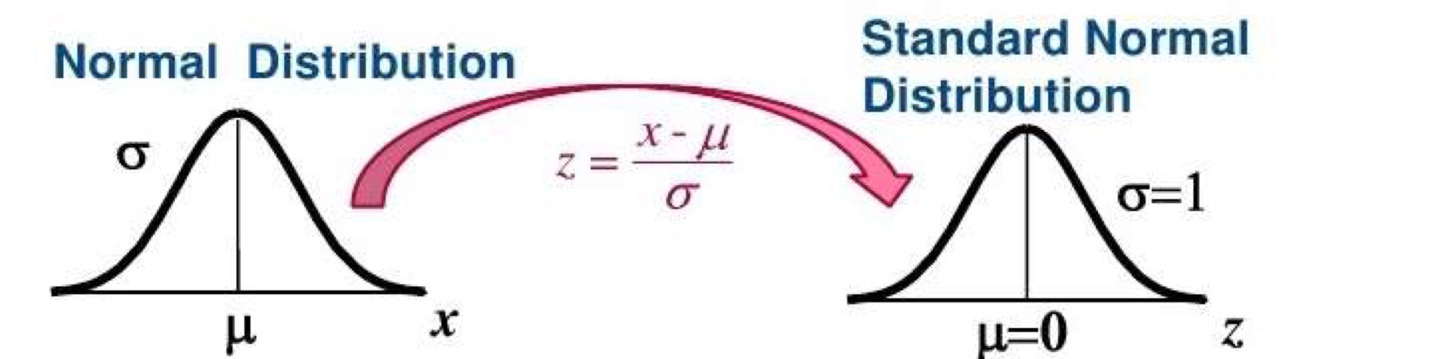
Standard normal distribution
표준정규분포
Z ∼ N ( μ , σ 2 ) Z\sim N(\mu,\sigma^2) Z ∼ N ( μ , σ 2 )
Z = X − μ σ Z=\frac{X-\mu} {\sigma} Z = σ X − μ
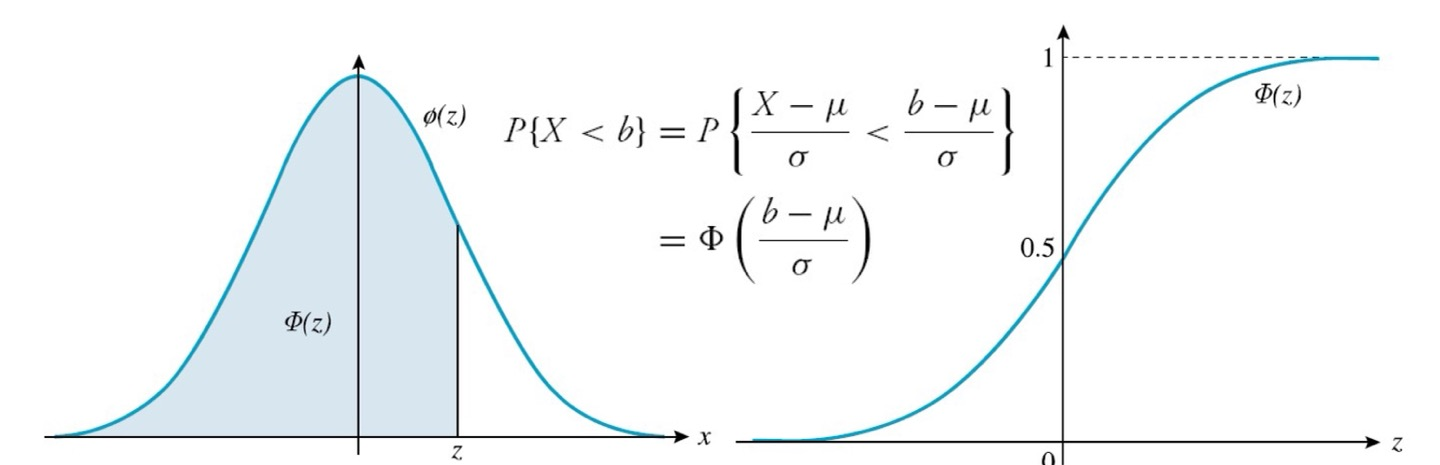
CDFΦ ( x ) = 1 2 π ∫ − ∞ x e − y 2 / 2 d y , − ∞ < x < ∞ \Phi(x)=\frac{1} {\sqrt {2\pi}}\int_{-\infin}^{x} e^{-y^2/2}\, dy,\qquad-\infin<x<\infin Φ ( x ) = 2 π 1 ∫ − ∞ x e − y 2 / 2 d y , − ∞ < x < ∞
For x>0Φ ( − x ) = P { Z < − x } = P { Z > x } = 1 − Φ ( x ) \begin {matrix} \Phi(-x) &=&P\{Z<-x\} \\ &=& P\{Z>x\} \\ &=&1-\Phi(x) \end {matrix} Φ ( − x ) = = = P { Z < − x } P { Z > x } 1 − Φ ( x )
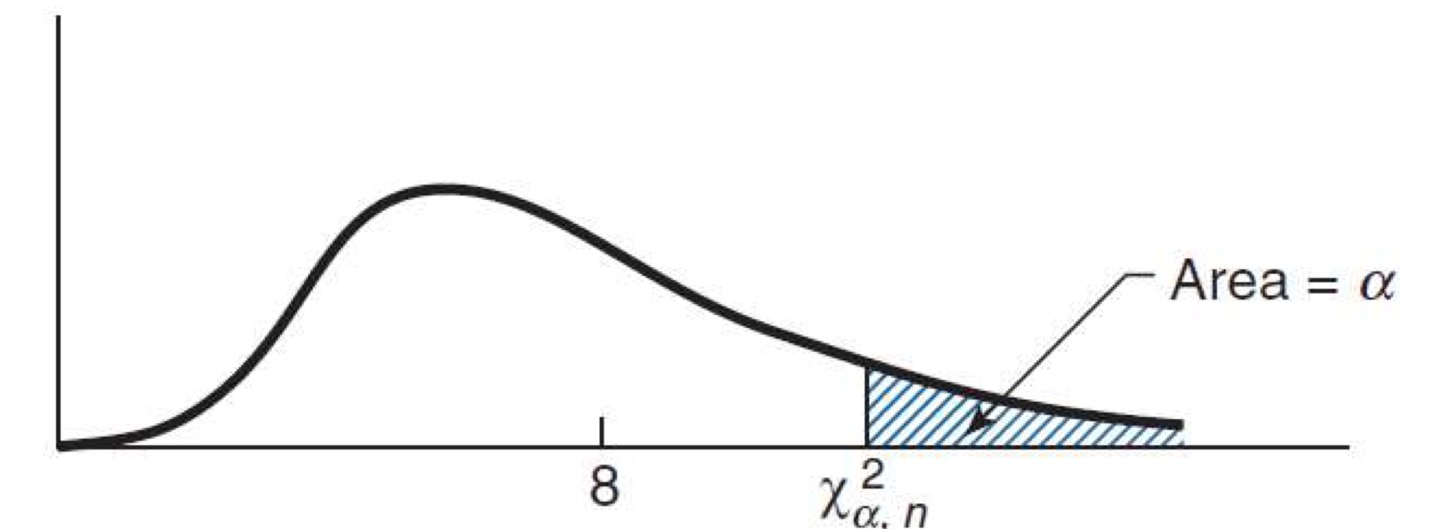
Chi-Square Distribution
카이제곱 분포
X ∼ χ n 2 X\sim \chi^2_n X ∼ χ n 2
표준정규분포에서 얻는 랜덤 변수들의 제곱합
χ 2 ( v = n − 1 ) → \chi^2(v=n-1) \rightarrow χ 2 ( v = n − 1 ) → v v v
S u p p o s e Z 1 , Z 2 , . . . , Z n a r e i n d e p e n d e n t s t a n d a r d n o r m a l r a n d o m v a r i a b l e s \mathrm{Suppose}\ Z_1,Z_2,...,Z_n\ \mathrm{are\ independent \ standard\ normal\ random\ variables} S u p p o s e Z 1 , Z 2 , . . . , Z n a r e i n d e p e n d e n t s t a n d a r d n o r m a l r a n d o m v a r i a b l e s X = Z 1 2 + Z 2 2 + . . . + Z n 2 X=Z^2_1+Z^2_2+...+Z^2_n X = Z 1 2 + Z 2 2 + . . . + Z n 2
Pdf
-Variance = 2n
For any a ∈ ( 0 , 1 ) , χ a , n 2 a \in(0,1),\chi^2_{a,n} a ∈ ( 0 , 1 ) , χ a , n 2 P { X ≥ χ a , n 2 } = a P\{X\ge \chi^2_{a,n}\}=a P { X ≥ χ a , n 2 } = a
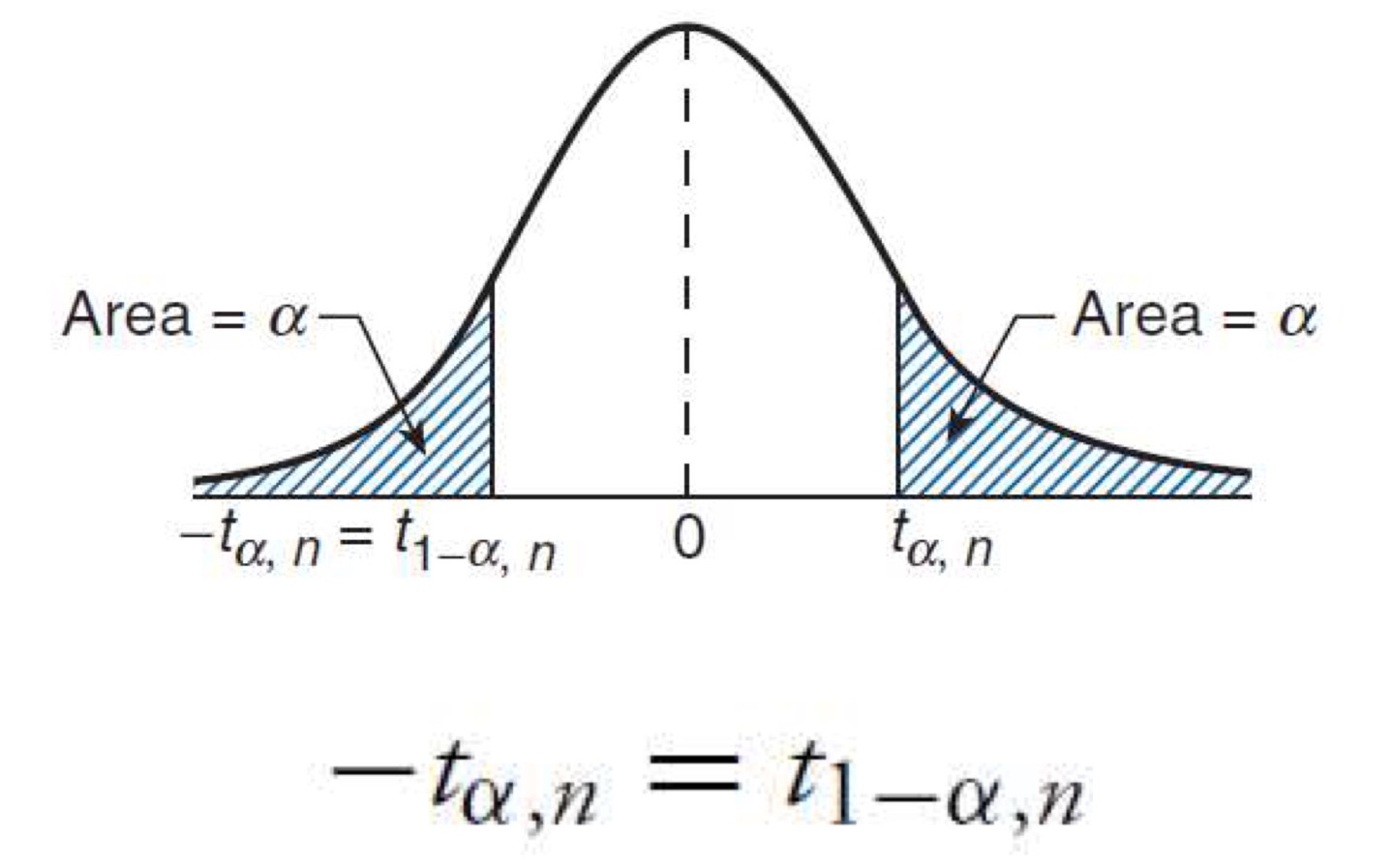
t-Distribution
t분포
T n = Z χ n 2 / n T_n=\frac{Z} {\sqrt{\chi^2_n/n}} T n = χ n 2 / n Z 이때 Z = S t a n d a r a d N o r m a l N ( 0 , 1 ) Z=\mathrm{Standarad Normal}\ \ N(0,1) Z = S t a n d a r a d N o r m a l N ( 0 , 1 ) n n n
PropertyE [ T n ] = 0 , n > 1 E[T_n]=0,\qquad n>1 E [ T n ] = 0 , n > 1 V a r ( T n ) = n n − 2 , n > 2 Var(T_n)=\frac{n} {n-2},\qquad n>2 V a r ( T n ) = n − 2 n , n > 2 a ∈ ( 0 , 1 ) , t a , n a\in (0,1),t_{a,n} a ∈ ( 0 , 1 ) , t a , n P { T n ≥ t a , n } = a P\{T_n\ge t_{a,n}\}=a P { T n ≥ t a , n } = a P { T n ≥ − t a , n } = 1 − a P\{T_n\ge-t_{a,n}\}=1-a P { T n ≥ − t a , n } = 1 − a
Sum of normal distribution Point Estimation
점추정
sample mean X ˉ \bar X X ˉ
X ˉ = X 1 + . . . + X n n \bar X=\frac {X_1+...+X_n} {n} X ˉ = n X 1 + . . . + X n
Unbiased estimator for expectation
E [ X ] ˉ = E [ X 1 + . . . + X n n ] = 1 n ( E [ X 1 ] + . . . + E [ X n ] ) = μ \begin{matrix} E\bar{[X]}&=&E[\frac{X_1+...+X_n}{n}]\\ &=&\frac{1}{n}(E[X_1]+...+E[X_n])\\ &=&\mu \end{matrix} E [ X ] ˉ = = = E [ n X 1 + . . . + X n ] n 1 ( E [ X 1 ] + . . . + E [ X n ] ) μ sample mean(E [ X ˉ ] E[\bar X] E [ X ˉ ] ≒ \fallingdotseq ≒ μ \mu μ
Variance of sample mean
sample variance S 2 S^2 S 2
S 2 = ∑ i = 1 n ( X i − X ˉ ) 2 n − 1 S^2=\frac {\sum_{i=1}^n (X_i-\bar X)^2} {n-1} S 2 = n − 1 ∑ i = 1 n ( X i − X ˉ ) 2
Unbiased estimator for expectation
Maximum Likelihood Estimator (MLE)
데이터 분포에 대한 파라미터를 찾을 때 자주 쓰임
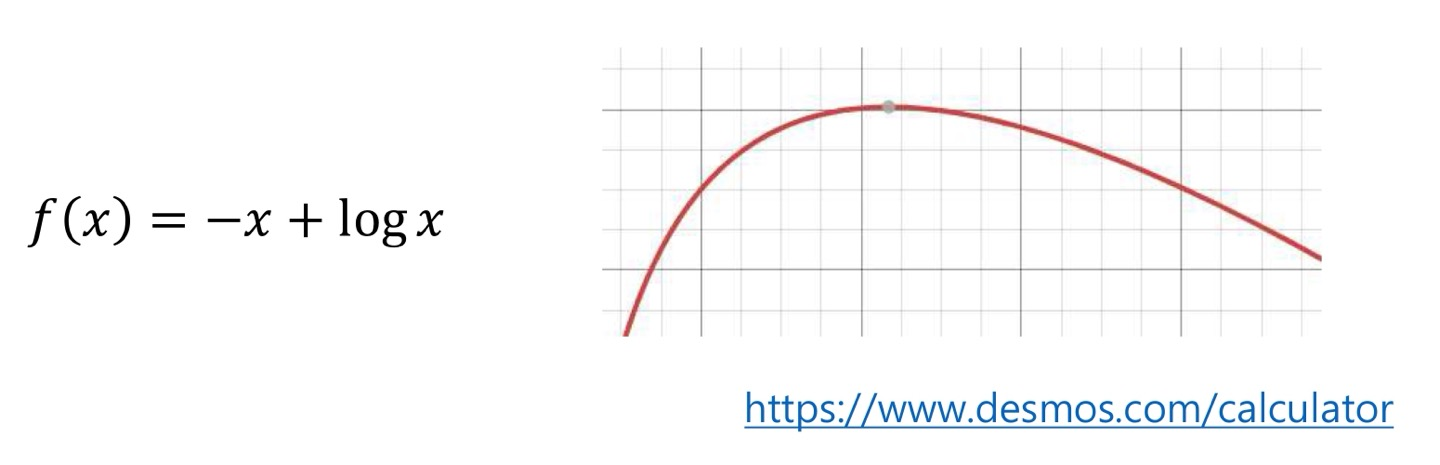
관측이 가능하다는 것은 그 만큼 자주 일어난다는 뜻 -> 자주 일어나는 그 event를 가장 잘 설명할 수 있는 파라미터 찾기 (값을 max하게 만들어주는)
MLE for Bernoulli RV
Bernoulli
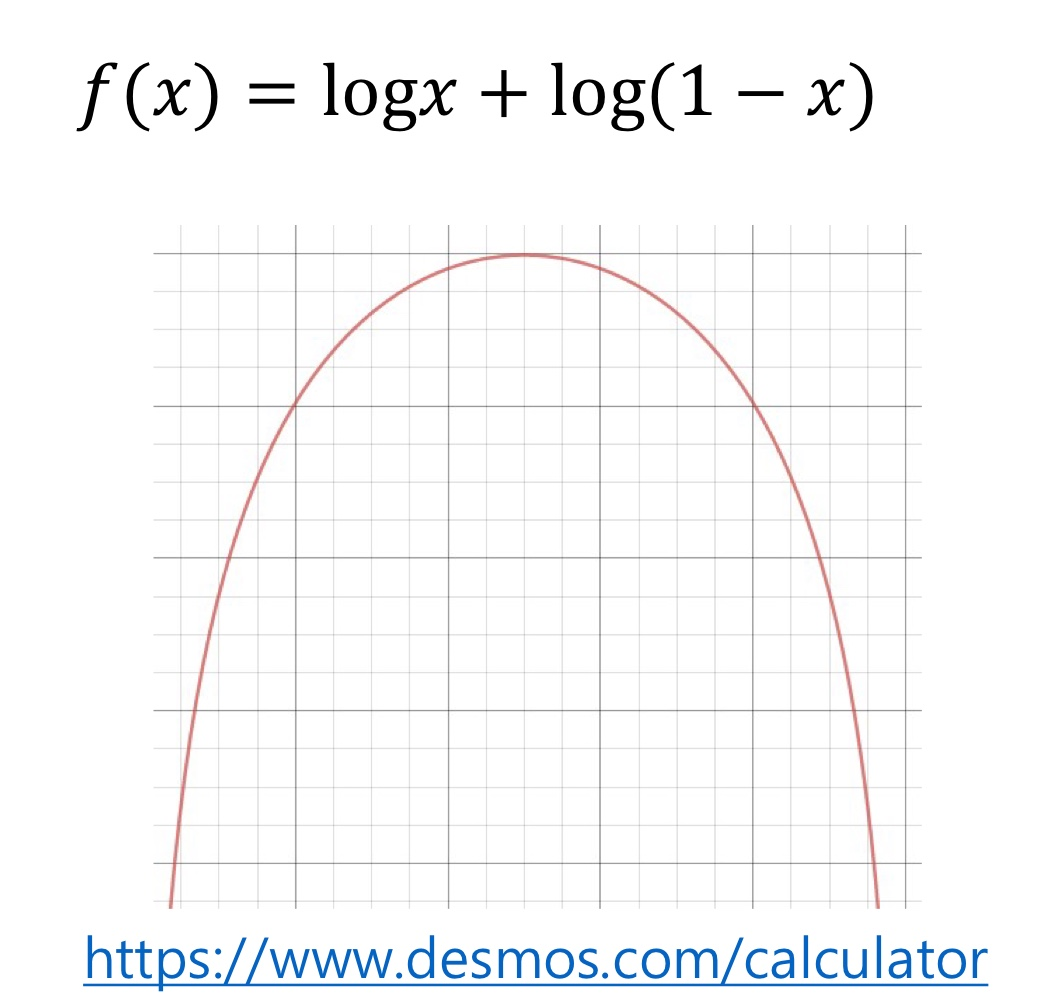
Log likelihood
MLE for Poisson RV
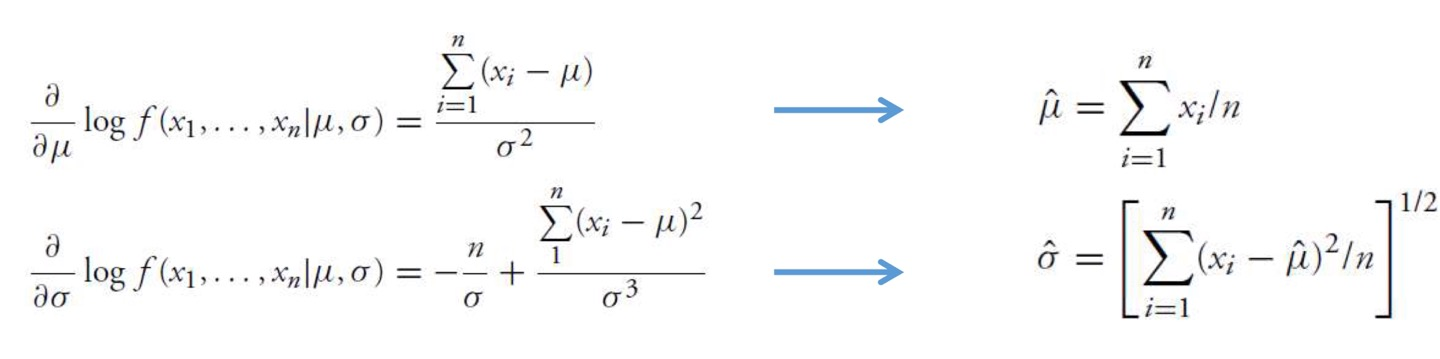
MLE for Normal RV
μ \mu μ σ \sigma σ
Law of large number (LLN)
큰수법칙
큰 모집단에서 무작위로 뽑은 표본의 평균이 전체 모집단의 평균과 가까울 가능성이 높다.
X 1 , X 2 . . . X_1,X_2... X 1 , X 2 . . . E [ X 1 ] = E [ X 2 ] = . . . = μ E[X_1]=E[X_2]=...=\mu E [ X 1 ] = E [ X 2 ] = . . . = μ
LNN states that
X ˉ = X 1 + . . . + X n n → n → ∞ μ \bar X=\frac{X_1+...+X_n}{n}\rightarrow^{n\rightarrow \infin} \mu X ˉ = n X 1 + . . . + X n → n → ∞ μ
Central Limit Theorem (CLT)
중심극한정리
모집단에서 표본 데이터를 뽑을 때, 모집단의 분포에 상관없이 (모집단이 정규분포를 따르지 않아도) 표본의 크기 n이 커질수록 표본평균 X ˉ \bar X X ˉ
StatementX 1 + . . . + X n − n μ σ n \frac{X_1+...+X_n-n\mu}{\sigma\sqrt{n}} σ n X 1 + . . . + X n − n μ
Binomial RV
E [ X i ] = p E[X_i]=p E [ X i ] = p V a r ( X i ) = p ( 1 − p ) Var(X_i)=p(1-p) V a r ( X i ) = p ( 1 − p ) CLT implies for large n,B ( n . p ) → X − n p n p ( 1 − p ) B(n.p)\rightarrow\frac{X-np}{\sqrt{np(1-p)}} B ( n . p ) → n p ( 1 − p ) X − n p
How large n is needed? n ≥ 30 n\ge30 n ≥ 3 0