Adaptive Normalization for Non-stationary Time Series Forecasting: A Temporal Slice Perspective

Abstract

딥러닝 모델은 시퀀스 의존성을 포착하는 능력 덕분에 시계열 예측 분야에서 발전되어왔다. 하지만 데이터의 비정상성은 여전히 도전 과제이다. 이를 위해서 정규화 작업을 통해서 비정상성을 줄이려는 여러 노력들이 이루어졌었다. 그러나 이러한 방법들은 일반적으로 입력 시계열과 예측 구간 시계열 간의 분포 차이를 간과하였고, 동일 인스턴스 내 모든 시간 점이 동일한 통계적 특성을 공유한다고 가정한다. 이를 해결하기 위해 우리는 독창적인 slice레벨의 적응적인 정규화 SAN을 제안한다. 이는 시계열 예측에서 더 유연한 정규와하 역정규화를 수행할 수 있다. SAN은 2개의 디자인을 포함하는데, 첫 번쨰는 SAN이 글로벌 인스턴스의 말고, 로컬한 인스턴스의 비정상성을 제거하고, 두번째로 SAN이 독립적으로 통계 특성의 트랜드를 모델링한다. 결과적으로 SAN은 일반화된 model-agnostic한 플러그인으로 시계열 데이터의 비정상성의 영향을 줄이게 된다. SAN은 다양한 데이터에 대해서 효과를 입증하였다.

Introduction

최근 많은 연구들이 비정상성을 제거하기 위해서 정규화 방법론을 통해 예측 퍼포먼스를 높였다. 하지만 이런 접근 방법론은 2가지의 한계점을 가지는데, 대부분의 모델들은 인풋 시계열과 예측 시계열의 분포 차이를 무시한다. 그리고 간단하게 인풋의 통계 특성을 활용하여 denormalize 할 뿐이다. 게다가, 이전의 연구들은 모든 포인트를 같은 instance라고 가정하였고 모든 통계적 틍성을 통합해서 보았다. 이러한 상세하지 않은 세팅의 경우에는 시간에 따라 많이 변하는 데이터에는 적합하지 않다.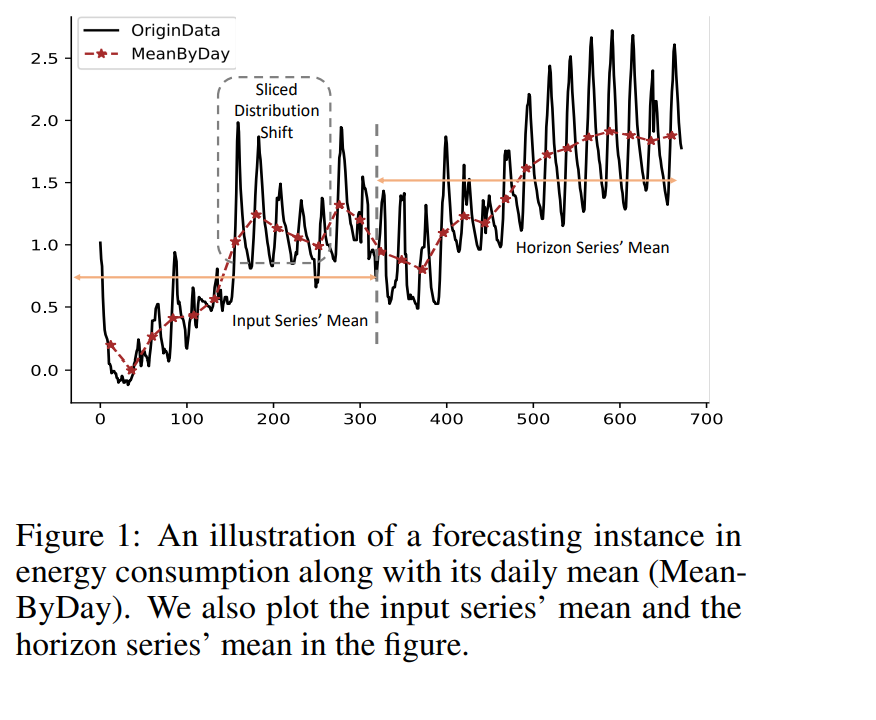
이와 같이 시계열의 평균은 많이 달라지게 된다. 이는 분포 변이로 나타나고, fine-grained slice level에서는 많은 차이가 난다. 따라서 글로벌하게 normalization 을 수행하는 것은 이러한 시계열에 적합하지 않다. 즉, 예측 shift로 인해 예측 정확도가 부정확하게 되는 것이다.
이러한 한계점을 극복하기 위해 general normalization 프레임워크를 SAN(Slicing Adaptive Normalization) 방법론을 제안한다.
구체적으로, 인풋 시퀀스가 겹치지 않게 동일한 사이즈로 split 되고 그들의 통계를 통해 normalized 된다. 그리고 예측 모델에 들어간다. 또한 통계 예측 모듈을 사용하여 future slice에 대한 분포를 예측한다. 마지막으로, 예측모델에서 나온 아웃풋에 통계 비정상성 정보가 재복원된다. 슬라이스 레벨 특성을 모델링함으로써 SAN은 비정상성을 local region 에서 제거할 수 있게 된다. 게다가, 통계 예측 모듈이 독립적으로 통계 특성을 모델링하기 때문에 SAN은 더 정확한 통계를 adaptive한 denormalization을 통해 예측하게 된다.
결과적으로, 비정상성의 예측 태스크는 통계 예측과 비정상성 예측으로 이루어진다. 게다가, SAN은 모델 어그노스틱하며, 임의의 예측 모델에 사용 가능하다. SAN은 기존의 정규화 방법론을 능가한다. 본 연구의 contribution은 다음과 같다.
1. 시계열에 비정상성을 고려한 SAN을 제안하여 일반화된 정규화 프레임워크를 제안한다. 이는 slice 관점에서 비정상성을 모델링하며, 비정상 팩터를 더 효과적으로 제거한다.
2. SAN을 위한 유연한 통계 예측 모델을 제안한다. 이를 명시적으로 미래의 분포를 예측함으로써, SAN은 비정상 예측 태스크를 divide and conquer 형식으로 간단화한다.
3. 충분한 실험을 9개의 실제 데이터셋을 통해 실험하였고, 결과는 SAN이; 다양한 메인스트림 예측 모델에 비해서 퍼포먼스를 높임을 보였다. 게다가, SAN과 SOTA 정규화 방법론을 비교하여 제안 방법론의 우수함을 입증하였다.

2 Related Works

2.1 Time Series Forecasting

ARIMA로 시작하여서 최근에는 딥러닝을 활용한 RNN등이 활용되고 있다. 이러한 아키텍처는 error accumulation 이슈가 있다. 이는 recursive한 inference 떄문이다. final 예측의 정확도를 높이기 위해서 많은 아키텍처가 long-range 의존성을 캡처하고자 하였고 있는 self-attention 매커니즘과 convoulution 네크워크등이 있다. 게다가, 시계열 데이터의 특성을 활용하기 위해서 최근 연구들은 trend-seasonal decomposition/time-frequency 변환과 같은 전통적인 방법들을 활용하기도 한다. 게다가, 최근 연구들은 간단한 선형 네트워크가 분해에 경쟁력있는 성능을 보이며, 이를 통해 slice-기반의 방법론들이 long time 시계열 예측 태스크에서 퍼포먼스를 입증하였다.

2.2 Non-stationary Time Series Forecasting

대부분의 시계열 예측 방법론은 temporal dependency를 포착하기 위해서 효과적인 아키텍처를 디자인하는데 우선되었다. 하지만 비정상성에 대한 점을 간과하였다. 딥러닝 기반의 모델은 학습과 테스트 데이터가 같은 분포를 가진다는 가정을 하기 때문에 이러한 불인치는 모델의 정확도를 낮춘다. 게다가, 학습셋 분포의 차이가 노이즈를 만들어내기 때문에 학습 태스크가 커버하기가 어렵다. 다양한 stationarization 방법론들이 연구되어왔다.
DDF-DA 방법로은 도메인 어탭테이션을 통해서 데이터 분포의 변화를 예측했다. DAIN은 비선형 네트워크를 통해 각 인스턴스에 대해서 적응적으로 정규화를 수행하였다. ST-norm은 2개의 정규화 모듈을 통해서 temproal과 spatial 관점에서 정규화를 수행하였다. 이후에 연구들은 비정상성은 정확한 예측을 위해서 필수이며, 간단히 이것들을 제거한다고 하였을 때에는 예측이 맞지 않았다. 그러므로, RevIN 에서는 대칭 정규화 방법론을 통해서 인풋 시퀀스에 대한 정규ㅘ를 수행하고, 모델 아웃풋에 대해서 역정규화를 수행하였다. Non-stationary 트랜스포머는 de-stationary attention을 통해서 non-stationary 팩터를 self-attention을 통해 수행하였고, 트랜스포머 기반 모델의 발전을 이루었다. 최근 연구들은 intra, inter 공간 분포 차이를 정의하고 분포 상관계수를 학습하여서 이 이슈에 대응하고 있다.
이러한 기존의 정규화 방법론들에 비해 비슷한 instance에 대해서 같은 통계 특성을 공유한다는 가정을 가지고 있다. 이것들과는 다르게 본 연구에서는 분포가 일정하지 않고, time slice에 대해서 이러한 inconsistency를 고려한다.

3 Proposed Method

general model-agnostic 한 정규화 프레임워크를 SAN9Slicing Adaptive Normalization)을 제안한다. notation은 다음과 같다.

3.1 Normalization

SAN은 슬라이스별로 통계량을 계산한다.

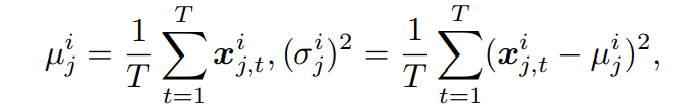
SAN은 각 슬라이스의 개별 통계량을 통해서 데이터를 정규화한다.

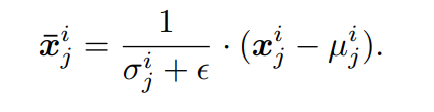
3.2 Statistics Prediction

SAN은 통계 예측 모델을 도입한다. 이는 다음과 같이 나타난다.

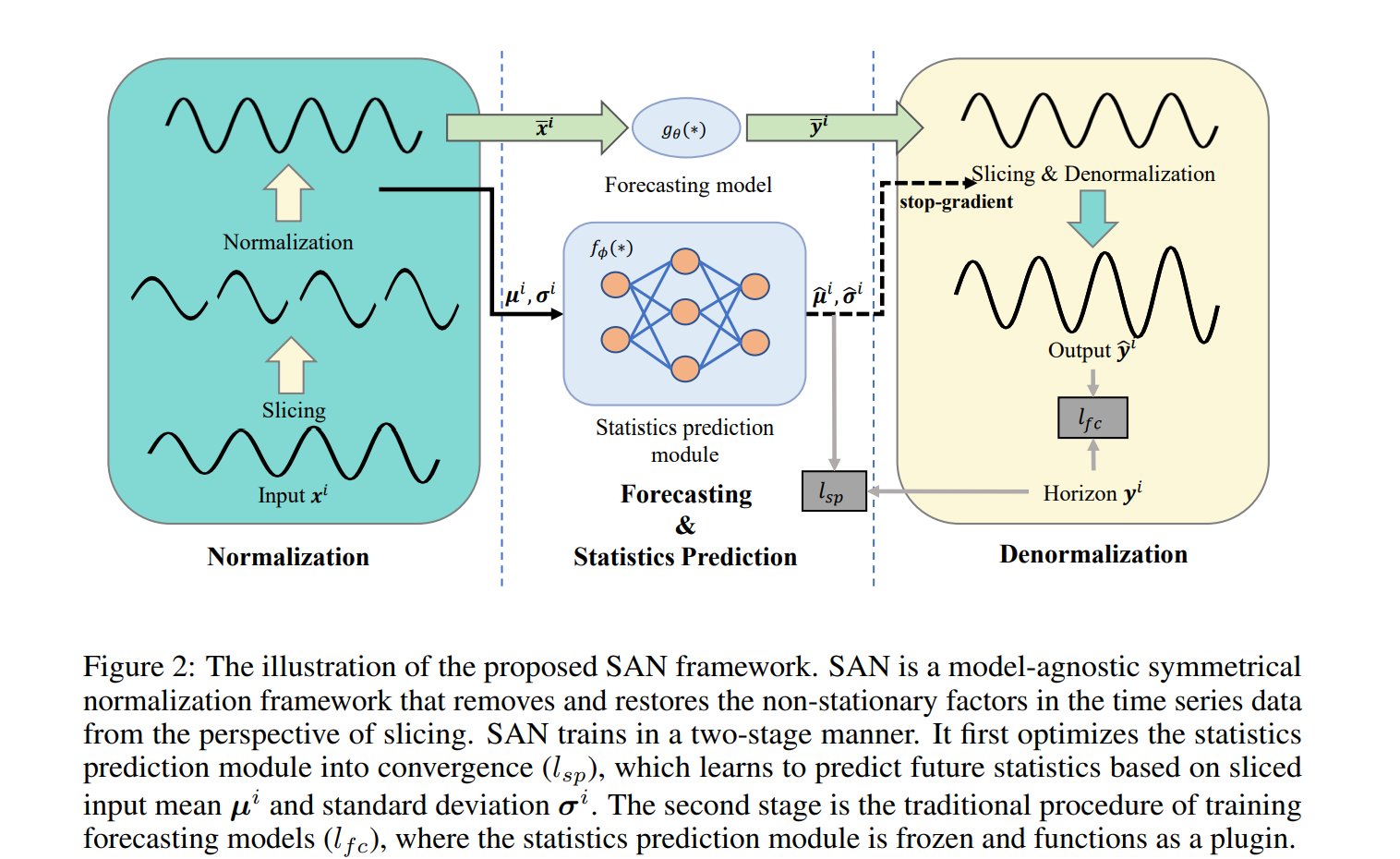
분포의 변이 학습을 통해서 미래 future slice의 분포를 예측하는것이다. 이는 2개의 레이어의 MLP를 통해서 간단하지만 효율적으로 학습한다. 이 통계량 예측은 SAN slice의 전체적인 퍼포먼스를 결정하고, 미래 분포의 비정상성을 복원하는데 핵심 역할을 한다.
구체적으로, 인풋 시퀀스의 평균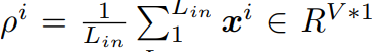
은 타겟 시퀀스의 평균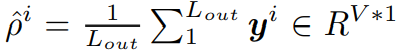
의 최대우도 예측값이라고 믿는다. 이러한 특성을 통해 현재의 방법론들은 전체 인풋 시퀀스의 통계량을 활용해서 아웃풋 시퀀스를 de stationarization을 한다. 하지만, 본 연구에서는 residual learning을 통해서 모듈이 미래 slice 평균과 전체적인 인풋 평균의 차이를 학습한다. 이는 특정 평균 값을 학습하는것이 아니라 residual만 학습하는 것이다. 이는 복잡도를 줄인다. 추가적으로, 스케일 변화에 대응하기 위해서, W1, W2 학습가능한 벡터를 활용하여 individual preference 을 제공하고 예측이 weighted sum으로 계산한다. 이런 통계 예측 과정은 다음과 같은 수식으로 나타난다.

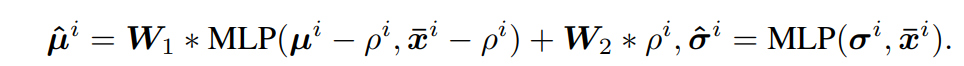
이를 통해서, 시계열의 비정상성을 모델링한다.

3.3 Denormalization

SAN은 정규화된 시퀀스를 예측모델에 넣고, 역정규화를 수행하여 예측 시퀀스의 비정상성을 복구한다. 이는 다음과 같이 수행된다.

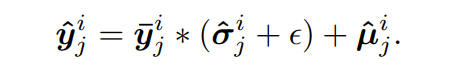
재복원 과정을 이와 같이 수행하면서, 시계열 순서대로 j를 나열하여 최종 예측을 만들어내고, 마지막에 퍼포먼스 평가를 위해 loss computation을 계산한다.

3.4 Two-stage Training Schema

전체적인 프레임워크가 간단한데, SAN의 정규화는 전체적인 학습 과정이 bi-level 최적화 문제이다. upper level의 목표는 시계열 예측의 정확도를 높이는 것이고, lower level의 목표는 실제값과 denormalized output의 분포 유사도를 높이는 것이다. 이는 다음과 같이 나타난다.
이러한 솔루션은 단순하기 때문에 모델 아키텍처와 훈련 과정을 쉽게 이해할 수 있다. 또한 효과가 좋은데, 통계 예측 모듈은 전체 훈련 셋에 대해 최적화되어 수렴하기 떄문에 미래 분포에 대한 신뢰할 수 있는 예측을 생성한다. 예측 모델은 정규화된 데이터에서 스케일에 영향을 받지 않는 패턴을 학습하는 더 간단한 작업을 처리할 수 있다. 이런 과정을 통해 비정상적인 시계열 예측을 위한 간결하면서도 효과적인 프레임워크를 설계할 수 있게 한다.

4 Experiments

4.1 Experimental Setup

Datasets
ETT/Electricity/Exchange/Traffic/Weather/ILI를 사용함

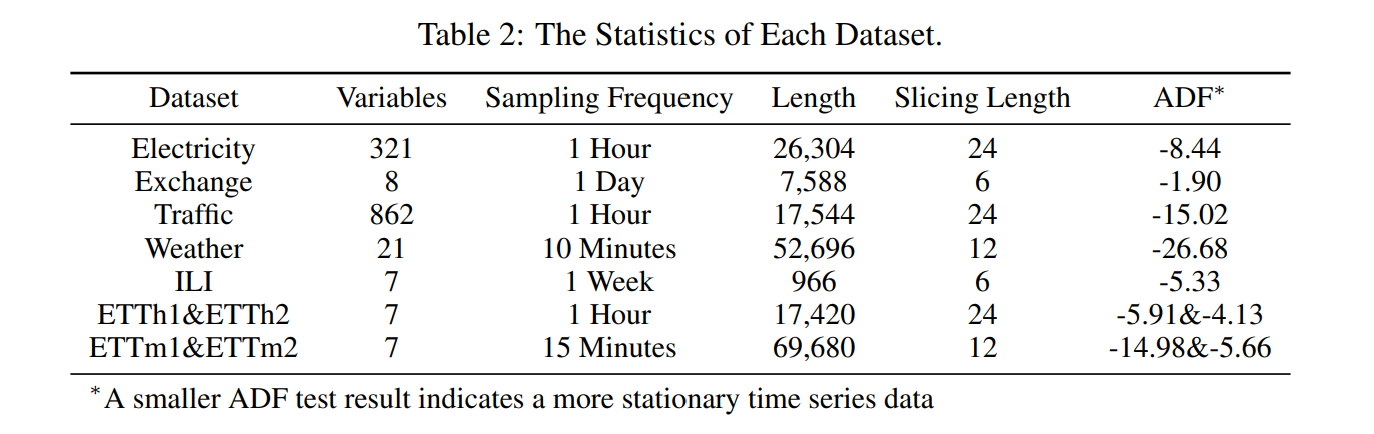
Backbone models
SAN이 모델에 상관없이 사용가능한 프레임워크이기 때문에 아무 예측 모델에 사용 가능하다. 따라서, DLinear, Autoformer, FEDformer, SCINet 에 사용되었다.
Experiments details
파이토치 및 RTX3090으로 수행하였다.
Slicing length
시계열 데이터는 실제 기간내에서 유사한 변화 패턴을 나타낸다는 휴리스틱 아이디어를 통해서 대부분의 설정이 의미 있는 시간 범위를 포함하도록 {6,12,24,48} 의 범위로 슬라이싱 범위를 설정했다.

4.2 Main Results

다변량 예측 결과는 다음과 같다.

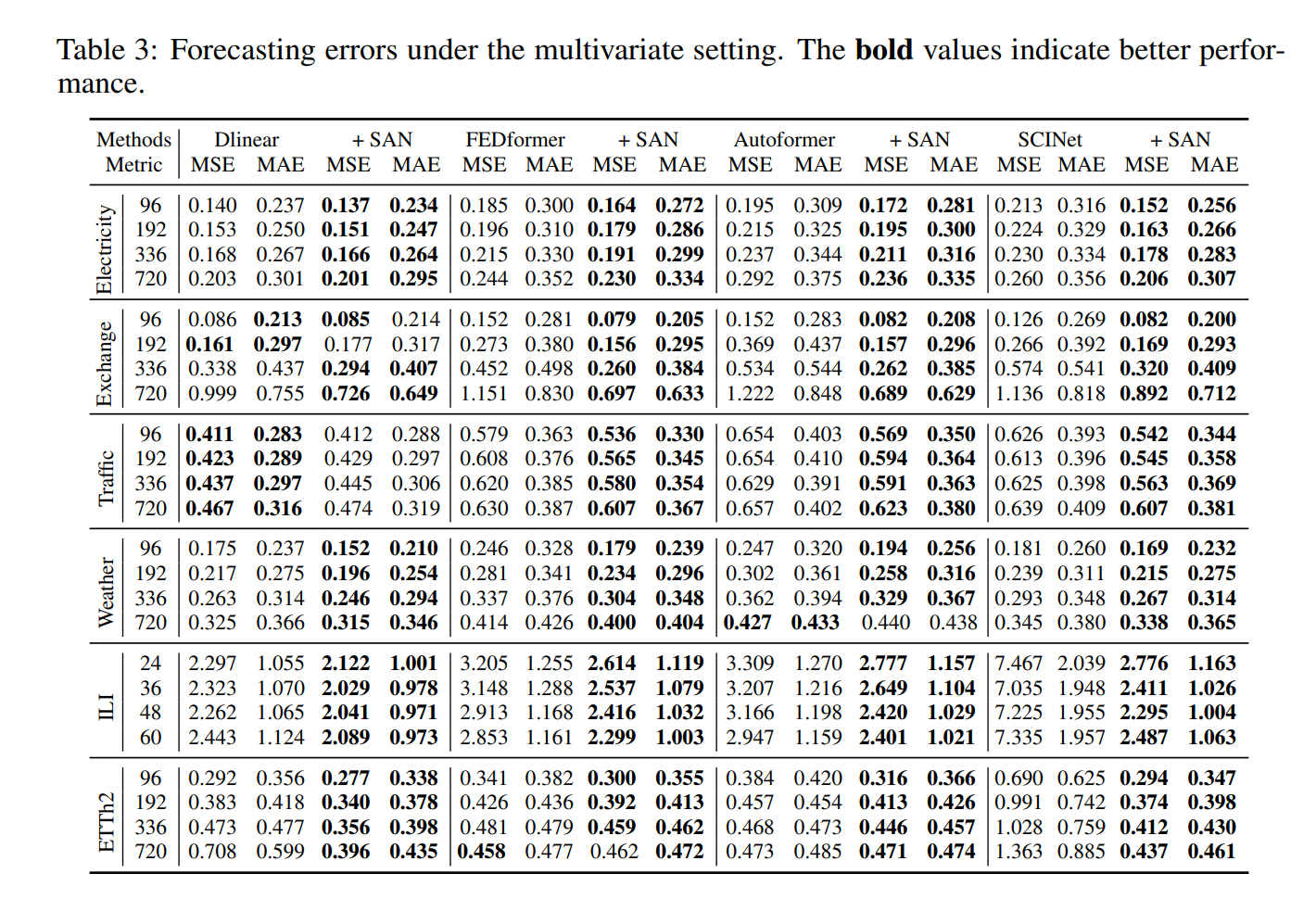
SAN 프레임워크가 명확하게 기존의 모델 대비해서 long-term 예측에서 성능이 좋음을 알 수 있다.

4.3 Comparison With Normalization Methods

RevIn, NST, Dish-TS 를 비교하였다. 이는 다음과 같다.

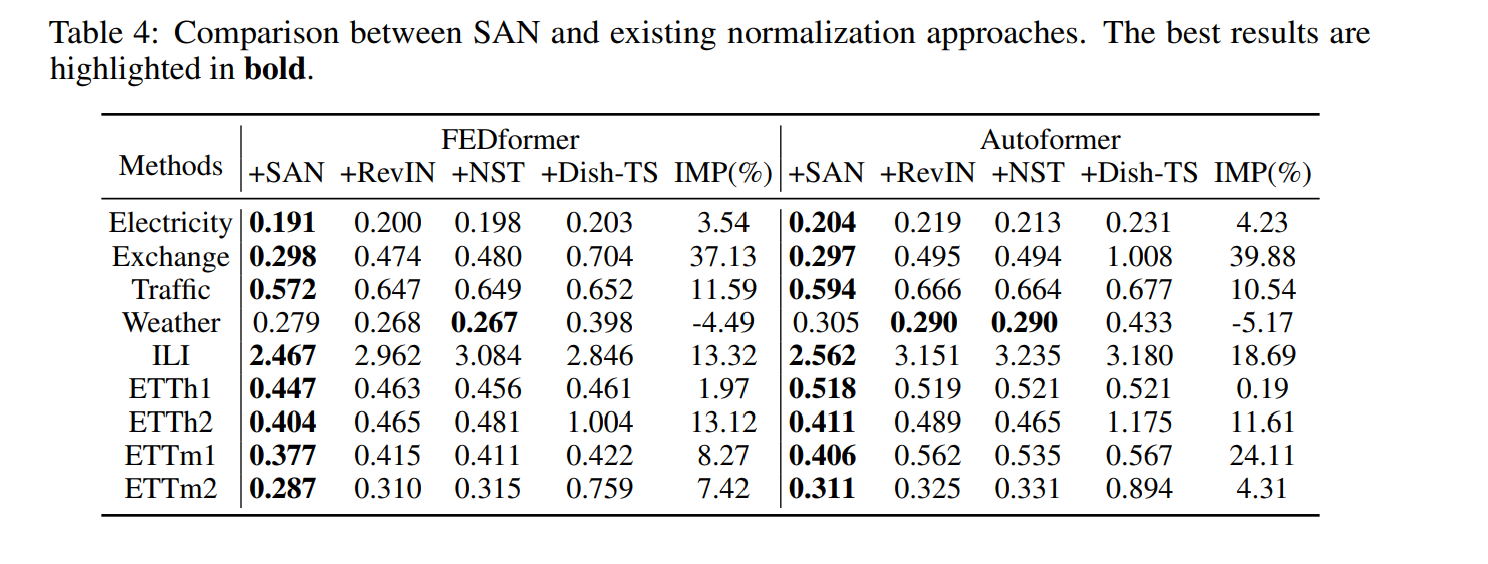
SAN이 존재하는 normalization 방법론 중에서 가장 성능이 좋음을 확인할 수 있다.

4.4 Qualitative Evaluation

시계열 예측에서 예측 결과의 품질은 지표 외에도 질적으로 평가될 수 있다.

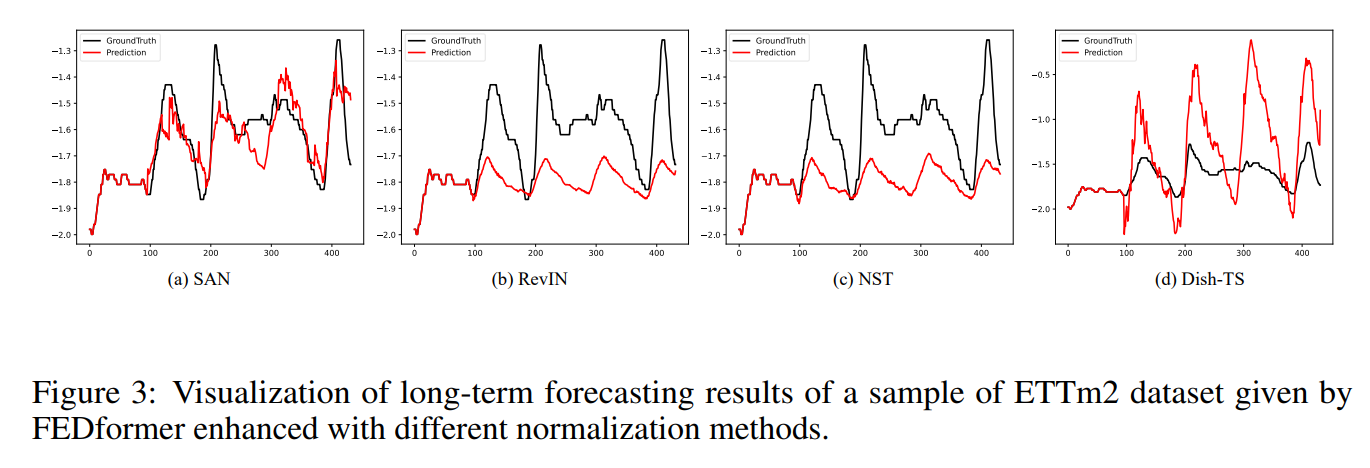
입력 길이는 96, 예측 길이는 336으로 설정 되어 있다. SAN이 현실적인 예측을 설정하는 반면에, 다른 모델들은 그렇지 못한다. RevIN 과 NST의 품질이 낮은 것은 이들의 역정규화 방식이 coarse 하기 떄문이다. 입력 시퀀스의 평균 값을 미래 데이터의 최대 우도 추정치로 간주하였지만, 비정상적인 데이터셋의 분포는 입력에 비해 크게 별하기 때문이다. 따라서 백본 모델의 출력을 단순히 역정규화를 한다면, RevIN과 NST 예측과 같이 스케일이 비슷해진다. SAN은 슬라이싱 관점에서 시계열의 동적 특성을 모델링하고, 독립적인 통계 예측 모듈을 도입하여서 미래 분포를 예측하였기 때문에 예측 결과의 스케일과 바이어스를 적응적으로 조절할 수 있다. 따라서 SAN은 실제 데이터와 일치하는 값을 생성한다.

5 Conclusion

본 연구에서는 slicing을 통해서 시계열 데이터의 비정상성을 완화하였다. SAN 프레임워크를 제안하였으며, 입력에서 비정상성을 제거하고 정규화하여 슬라이스 단위로 비정규화를 통해 출력으로 재복하는 model-agnostic 한 프레임워크이다. 새로운 통계 예측 모듈을 통해 SNA은 비정상성 예측을 통해 모델의 성능을 높였다. SAN은 주요 예측 모델의 성능을 크게 개선하였으며, 슬라이스 관점에서 시계열을 모델링하는 추가 연구를 촉진시키고자 한다.