Peri-midFormer: Periodic Pyramid Transformer for Time Series Analysis

Abstract
시계열 분석은 날씨 예측이든지, 이상치 탐지, 행동 인식과 같은 태스크에서 많이 활용되고 있다. 이전 방법론들은 temporal variations을 1D 시계열로 바로 모델링하였다. 그러나 시계열의 데이터 포인트의 이산적 형태와 주기적 variation 의 복잡성 때문에 문제가 되었다. 주기성은 여러가지로 이루어져, 년도, 월, 주, 일 등 다양하다. 이전 방법론의 한계를 풀기 위해서 복잡한 주기적 variations들을 decouple하고, 다른 레벨의 주기적 컴퍼넌트들간의 관계를 multi-periodicity를 모델링하여 내제된 관계를 표현한다. 이는 시계열에서 피라미드와 같이 나타나며, 탑 레벨이 오리진 시계열이고, 로워 레벨이 periodic 컴퍼넌트로 지속적으로 올라갈수록 주기가 짧아진다. temporal variation을 좀 더 상세히 모델링 하기 위해서 주기적 컴포넌트들의 self-attention layer를 활용하였다. 우리가 제안하는 Peri-midFormer는 시계열 분석 태스크에서 SOTA 성능을 보였다.

1. Introduction

기존의 Timesnet 과 같은 방법론은 1D 시계열을 2D tensor로 변환하여 intra와 inter 주기성을 2D 상에서 융합하였다. 하지만, 이 방법론은 주기성간의 내제된 관계를 간과하여 CNN 특질 추출방법을 잘 활용하지 못했다.
우리는 시계열의 주기적 컴포넌트의 포함, 중첩 관계를 측정하고 복잡한 temproal variations에 대해서 다룬다. 실제 시계열은 다양한 periodicities를 포함하고 이들은 명백한 관계를 가진다. 서로다른 주기 레벨뿐 아니라, 같은 주기 레벨에서도 이러한 관계가 존재한다. 또한 long period는 다양한 short ones로 분해가 가능하여 피라미드 형태를 만든다.
이러한 분석에 따라, 시계열을 멀티플 주기적 컴포넌트로 분해하고, 피라미드 구조를 형성하여 긴 컴포넌트가 짧은 컴포넌트를 포함하게 만든다.

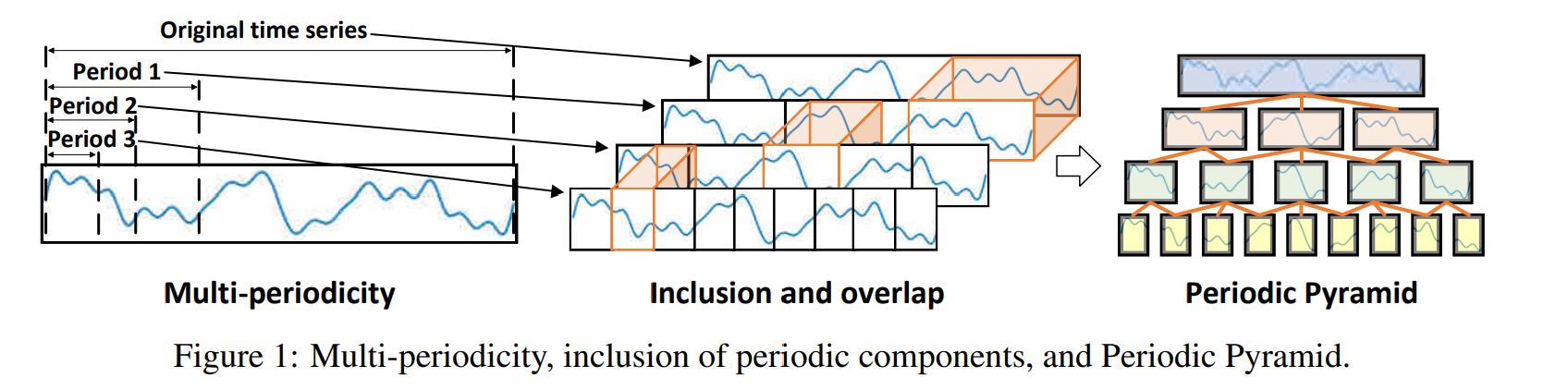
Fig.1은 periodic inclusion 관계에 대해서 표현하는데, 각 레벨은 같은 주기의 컴퍼넌트로 구성되어 있으며, 다른 레벨은 포함 관계를 의미한다. 이러한 변환은 original 1D 시계열을 2D representation으로 나타냄으로써, 다양한 주기의 관계를 표현하게 된다. 이 피라미드에서, 하나의 주기 컴포넌트는 2개의 상위 주기 컴포넌트에 포함될 수 있다. Peri-midFormer는 self-attention으로 이루어져 있다. 또한, peridoic pyramid의 각 가지는 periodic feature flow로 고려하고 특질을 모아 다운스트림 태스크에 더 양질의 정보를 제공한다. 실험을 통해 SOTA 퍼포먼스를 보였다.
1. 시계열의 다양한 주기적 포함 관계에 기반하여 본 연구는 탑-다운으로 구성된 주기의 피라미드 구조를 채택하였고, 1D 시계열을 2D 로 변환하여서 내재된 멀티 주기 관계를 시계열을 표현하였다.
2. Peri-midFormer를 제안하여서, 같은 레벨의 주기적 컴포넌트에 대해서 자동으로 의존성을 캡처하고, 다양한 temproal variations를 추출한다. 추가적으로 Peri-midFormer의 약잠재력을 활용하고자, Periodic Feature Flows를 도입하여 다운스트림 태스크에 다양한 정보를 제공한다.
3. 가지의 메인스트림 시계열 분석 태스크에 활용하여서 SOTA를 달성하였고 시계열 분석에서 우월한 주기적 정보를 제공하게 된다.

2 Related Work

시계열 분석에서 트랜스포머 기반 연구들이 좋은 퍼포먼스를 보였다. 이들은 어탠션 매커니즘을 활용하여 시계열 포인트들에 대해서 temporal 의존성을 드러내었다. AUtoforemr는 Auto-correlation 매커니즘을 통해서 시계열의 temproal 의존성을 캡처하였다. tempral 패턴의 복잡성을 다루기 위해서 deep decomposition 아키텍처를 통해서 시즈널과 트랜드를 인풋 시계열에서 분해하였다. FEDformer는 시즈널과 트랜드 분해를 MOE 디자인을 통해 소개하였고, sparse attention을 주파수 도메인에서 수행하였다. pyraformer는 다운-탑 피라미드 구조를 시계열의 멀티 conv 연산을 통해 트랜스포머에서 긴 정보의 propation path 이슈를 해결하였다. 이를 통해 타임과 공간 복잡성을 줄일 수 있었다. PatchTST는 개별 데이터 포인트를 패치로 파티션화 하여 토큰으로 활용하여 트랜스포머에 넣어 지역적 정보를 이해하는데 도움을 주었다. 또한 PatchTST는 각 채널을 독립적으로 프로세싱하여서 예측 태스크에서 좋은 성능을 보였다.
또 최근 연구에서는 Timesnet은 복잡한 temporal 패턴들에 대해서 멀티 주기성을을 탐색하여 temproal 2D variations 에 대해 캡처하고 CV CNN 백본에 활용하여 특질을 추출하였다. GPT4TS 는 LLM 모델을 GPT2를 pretrained 모델로 활용하였고, 시계열을 통해 파인튜닝하고, SOTA 결과를 보였다. FITS는 시계열 분석을 모델 기반의 주파수 도메인 동작에서 수행하여 아주 낮은 파라미터만을 활용하였다.
최근 연구들은 시계열의 멀티 스케일 정보를 활용한다. PDF는 숏텀과 롱텀 variation을 멀티 주기 디커플링 블럭을 통해 1D 를 2D로 변환한다. 이를 통해 정확한 예측을 수행하였다. SCNN은 다변향 시계열을 롱텀, 시즈널, 숏텀, co-evoling, residual components로 분해하여서 해석력을 높이고 distribution shift에 대응하였다. TimeMixer는 멀티스케일 믹싱 방법을 통해서 시계열을 coarse 스케일로 분해하여서 디테일 그리고 대형 variation 으로 나눈다. Past Decomposable Mixing을 통해 과거의 정보를 추출하고, Future-Multipredictor_mixing 을 통해서 멀티스케일의 예측 정확도를 높이고, 예측 태스크에서 좋은 성능을 보였다.

3 Methodology

3.1 Model Structure

Fig2. 에 상세한 구조가 나타난다. 탑에서 원본 시계열을 임베딩하는것으로 시작한다. FFT를 통해서 멀티플 주기 컴포넌트를 다른 레벨의 다른 길이로 분해한다. 이들은 포함 관계를 나타낸다. 더 내려가면, 패딩과 프로젝션을 통해서 하나의 차원이 되게끔 한다. 각 컴포넌트들은 독립된 토큰으로 처리되며 positional embedding이 수행된다. 이들은 Peri-midForemr에 들어가 어탠션이 이루어지고 마지막으로 태스크에 따라 classification시 컴포넌트들이 컨캣되어 카테고리 공간에 직접 프로젝션된다. 다른 재구성 태스크에 대해서는(예측, 임퓨테이션, AD의 경우에는 인풋 길이혹은 채널 차원을 재구성해야 하기 때문에 재구성태스크라고 지칭함), 다른 피라미드에서의 특질들은 Periodic Feature Flows aggregation을 통해서 마지막 아웃풋을 만들어낸다. de-normalization과 deocomposition을 통해서 방법론의 효과를 최대화한다.

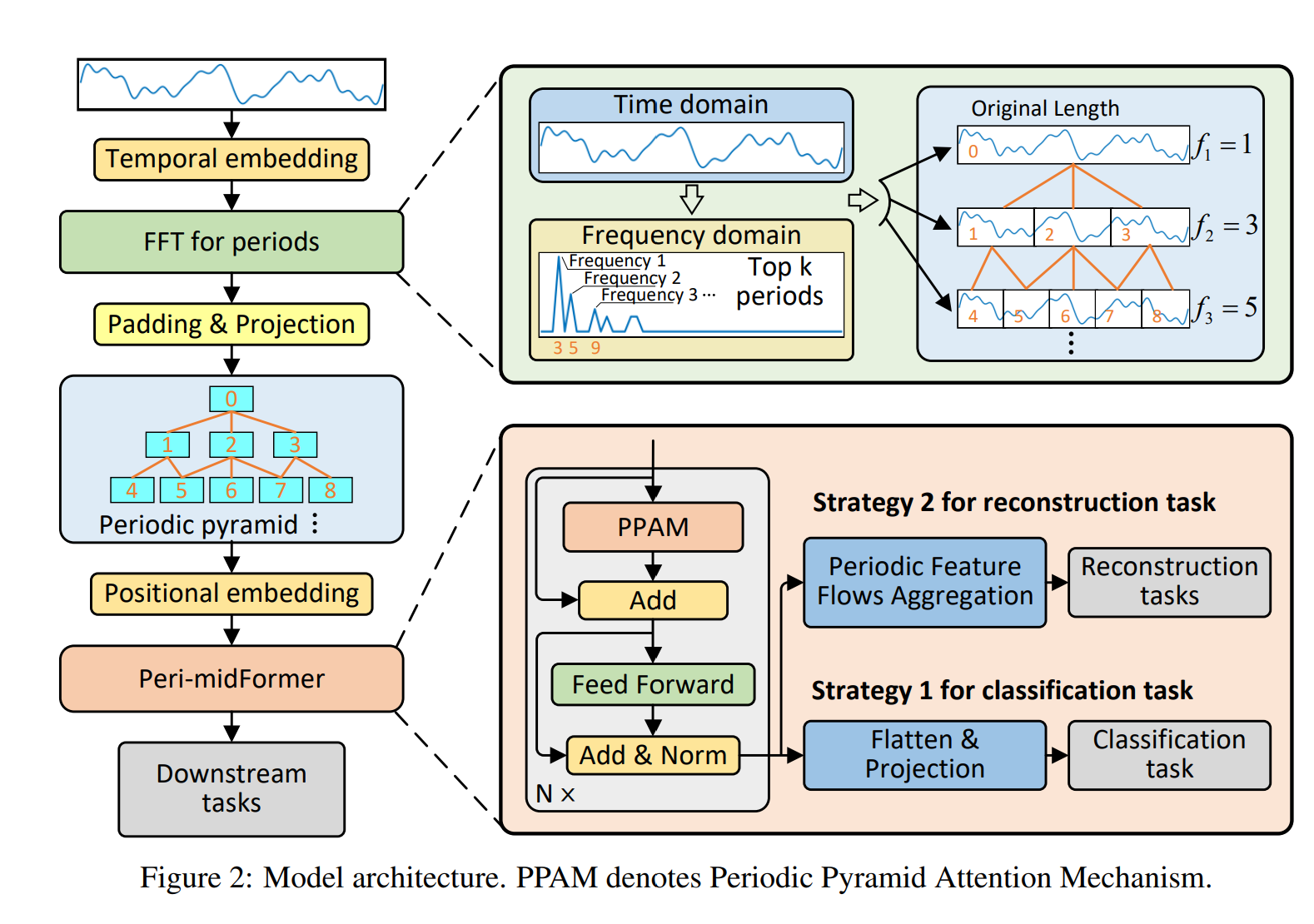
3.2 Periodic Pyramid Construction

원본 시계열 L 길이의 C 채널이 있다

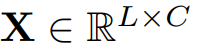
이때 seasonal part로 분해하고, trend 는 제거한다.

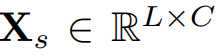
시즈널 파트를 파티션화하여 주기컴포넌트를 만든다. 이때 채널 C 는 유지하는데, 각 채널을 독립적으로 연산을 수행한다. FFT를 통해서 다음과 같이 주기 컴포넌트가 계산된다.

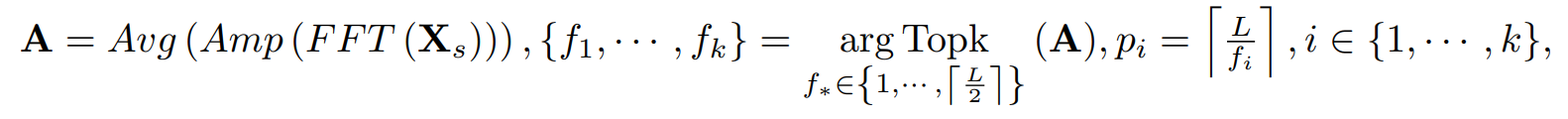
A는 각 채널의 주파수 성분을 평균했기 때문에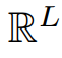
차원을 가진다.
Aj 는 j 주파수 주기 basis function의 intensity로, periodic length 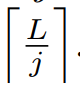에 대응되는 값이다.
그러니까, Aj는 전체 길이를 j로 나눈 길이만큼의 주기의 basis function intensity이다. 고주파의 노이즈를 제거하고, 주파수 도메인의 sparsity를 없애기 위해서, top-K amplitude 값 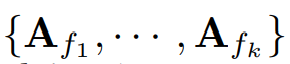이 선택되는데,
각 주파수 성분에서 가장 중요한 주파수의 Aj가 선택되는 것이다. k는 하이퍼 파라미터이며, 2에서 시작된다. 추가적으로, 피라미드 구조의 탑 레벨이 원본 시계열을 나타낼 수 있게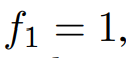
로 두고, 다른 주파수를 오름차순으로 둔다. 이 k 주기 길이에 따라 선택된 주파수들은 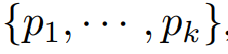내림차순으로 정리된다.
주파수 도메인의 conjugacny에 의해서,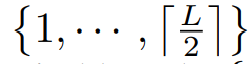
만 고려한다. 이러한 선택된 주파수들 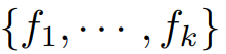은 perdiod 길이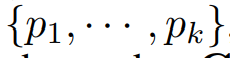
에 의해 선택되었으며, 원본 시계열을 주기 컴포넌트를 각 피라미드 레벨로 파티션화 되는데, 이는 다음과 같이 나타난다.

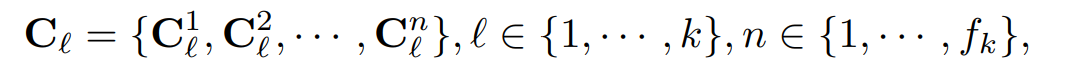
Cl 은 각 피라미드 레벨의 컴포넌트를 의미하며, Cln 은 l의 피라미드 레벨의 n번째 주기성 컴포넌트를 의미한다. l은 피라미드 레벨 인덱스로 탑에서부터 시작하여 증가하고, k까지 증가하게 된다. n은 컴퍼넌트 인덱스로, 왼쪽에서 오른쪽으로 증가하며, fk의 값만큼 증가하게 된다. 따라서 주기 피라미드는 다음과 같이 나타난다.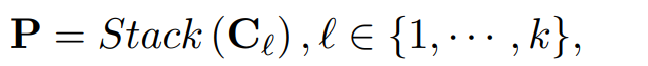

정리하자면, 원본 시계열 FFT변환 복소수를 제외한 AMP의 채널을 평균낸 값이 A
A에서 큰 순서대로 k개만큼(하이퍼파라미터)를 찾아 주파수값을 내림차순으로 {f1, f2, ... fk}.
이때의 amp 값은 {Af1, Af2 .... Afk} 이렇게. 단지, f1 = 1 로 두어서 원본 시계열 길이를 j=L을 반영한값이 제일 앞에 오게 함. 따라서 이렇게 선택된 주파수들은 다시 내림차순으로 period length는

가 된다.
원래는 샘플링 rate과 시간이 존재해야 주파수 값들을 명시적으로 표현할 수 있는데, 다양한 시계열 데이터셋에서 활용하기에는 불가능하기 떄문에 perioidic length 라는 상대적인 주기 길이로 표현하는것이다.
즉, 다변량 시계열에서 FFT 변환을 하고 amp만 추출한 뒤, 각 freq 값에 따라 평균을 한뒤 amp가 top K 만큼 큰 freq 찾는다. freq별로 다시 오름차순으로 재정렬하는것이다. 이때 p는 periodic length로 내림차순이 될 것이다. 왜냐면 freq는 오름차순인데, L/j 이므로 내림차순이 됨. 이것을 각 피라미드 레벨에 따라 파티션화 한 것이 Cl이고 이걸 레벨에 따라 모은게 최종 피라미드 P이다.

R은 주기 컴포넌트들간의 위에서 아래 관계로 정의하자면, 오버랩이 존재하냐 안하냐에 따라 다음과 같이 나뉜다.

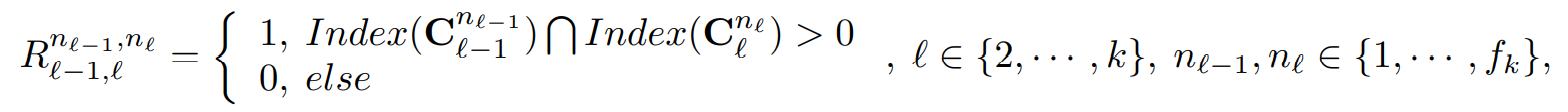
R = 1 이라면, 포함 관계가 있다는 것이고, R = 0 이라면 오버랩이 없다는 것이다. 이는 다음과 같이 그림으로 나타낼 수 있다.

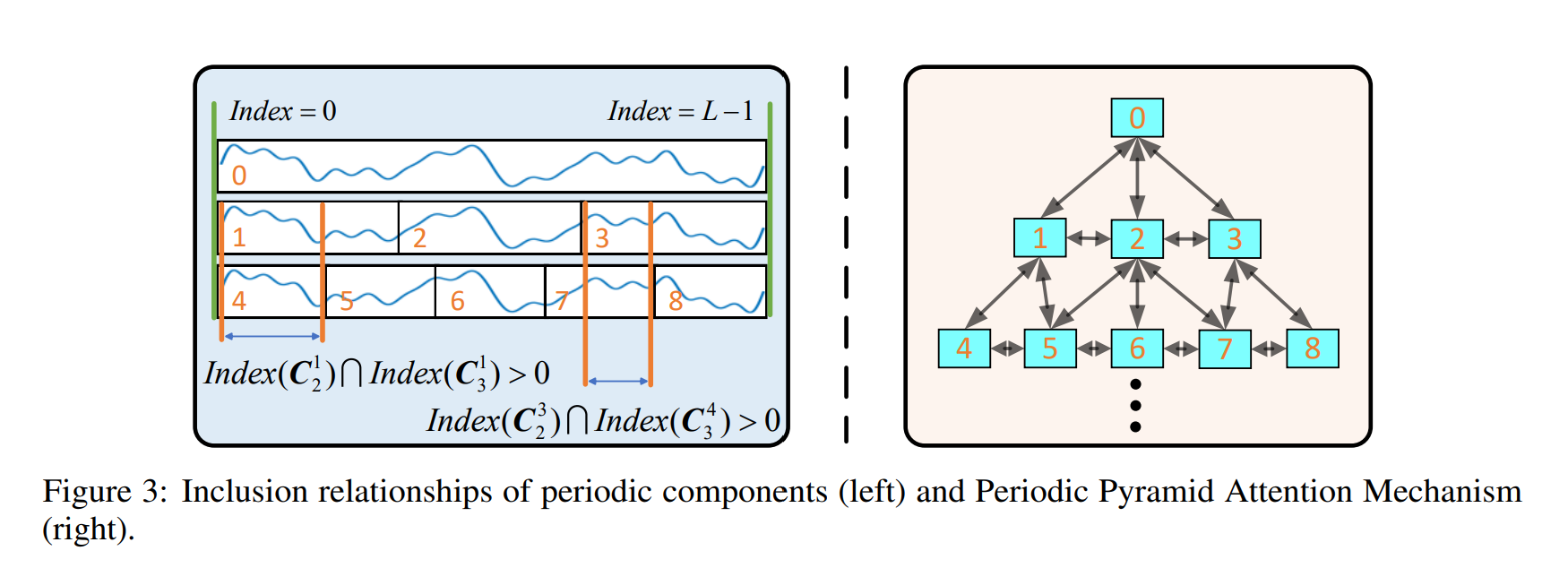
이러한 관계를 하위 어탠션 매트릭스에서 마스킹하는데 사용된다. 다른 레벨에 따른 이러한 주기 컴포넌트간의 관계는 복잡한 1D 시계열 정보를 명시적으로 표현한다. 또한 컴포넌트들간의 길이를 맞추기 위해 다음과 같은 식으로 나타낸다.

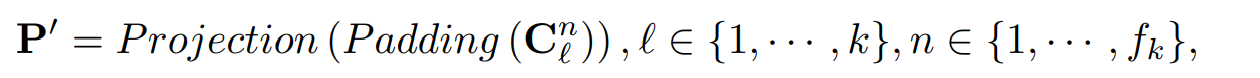
3.3 Periodic Pyramid Transformer (Peri-midFormer)

Periodic 피라미드가 만들어지면, Peri-midFormer의 인풋으로 넣는다. Periodic Pyramid Attention Mechanism (PPAM) 우리가 불리는 매커니즘은 Fig3. 의 오른쪽에 나타나있다. 원래의 conntection은 양방향으로 바뀐다. PPAM의 Inter level은 레벨 간의 period 의존성에 집중하고, Intra level의 attention은 같은 레벨의 의존성을 고려한다. Intra에서 바로 인접한 패치만이 고려되는 것이 아니라, 모든 패치쌍간의 관계가 고려딘다. 하지만 명확성을 위해 모든 어탠션 커넥션이 사는것아니다.
Cln은 3가지 타입의 커넥션이 존재한다. 위 레벨 parent 노드의 커넥션 P, 같은 레벨 모든 컴퍼넌트 노드의 커넥션 A, child 노드의 커넥션 C 이다.

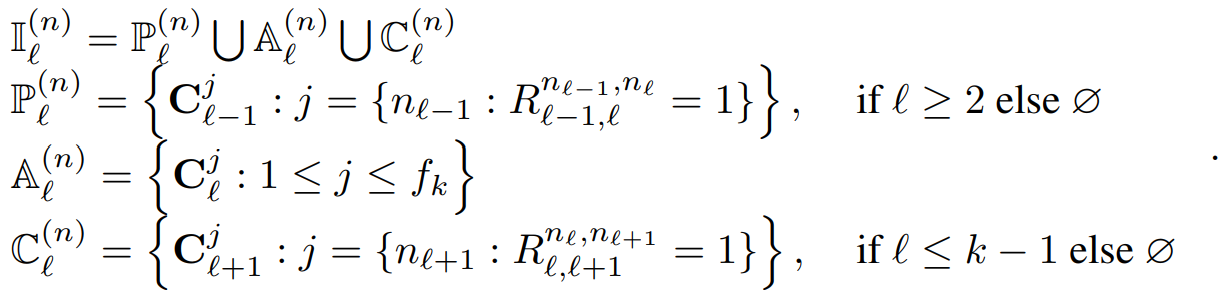
Cln 컴포넌트의 어텐션은 다음과 같이 나타난다.

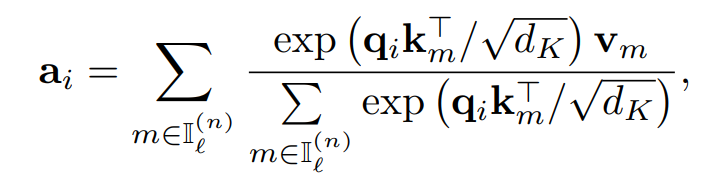
이를 모든 컴포넌트간의 어탠션을 통해서 통해 자동적으로 의존성을 고려하게 된다.

3.4 Periodic Feature Flows Aggregation

e Periodic Feature Flows Aggregation은 재구성 태스크에서 사용된다고 언급하였었다. Peri-midFormer의 아웃풋은 피라미드 구조를 유지한다. 이러한 다양한 주기 컴포넌트간 정보를 활용하기 위해서, 하나의 가지를 탑에서 바텀으로 periodic feature flow로 이름짓는다. 이는 Fig 4. 에서 나타난다.

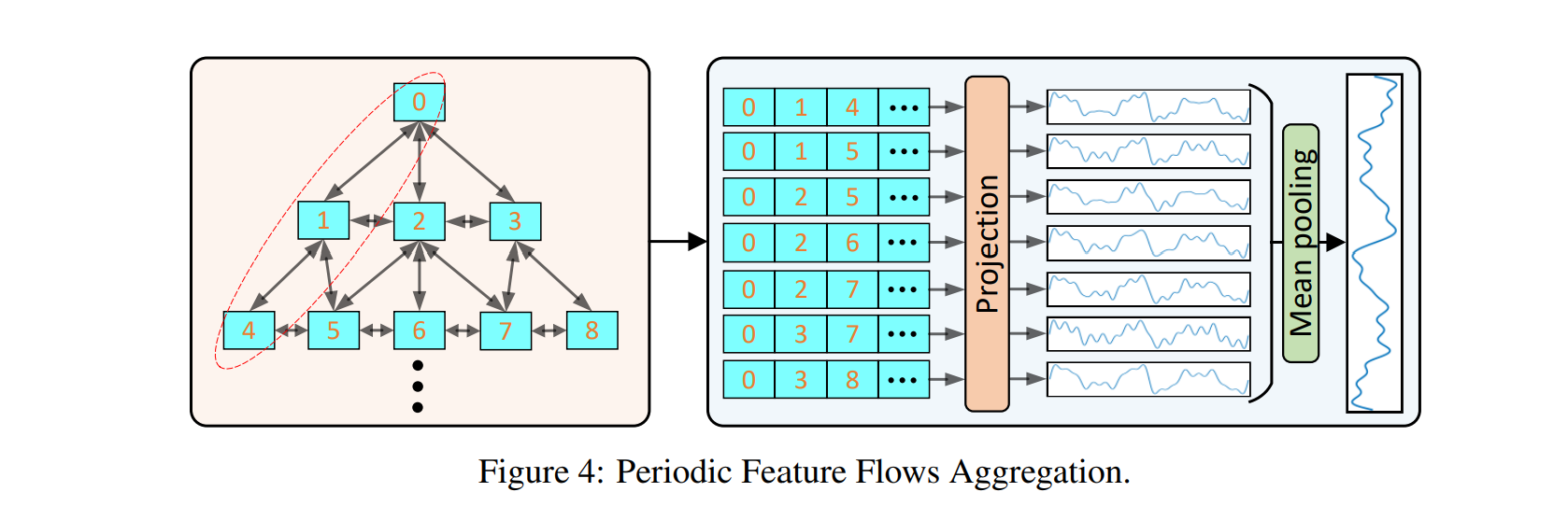
이는 시계열에서 서로다른 스케일의 특질을 나타낸다. 게다가, 각 레벨의 variations에 따라서, 각 특질 flow는 독립적인 정보를 제공한다. 그러므로, multiple feature flows를 통합하여서 Periodic Feature Flow Aggregation이라고 이름짓는다. 이것은 선형 프로젝션을 통해서 타겟 시계열 길이로 맞춰주고, 멀티 피처에 대한 플로우를 평균하여 Ys를 만든다.

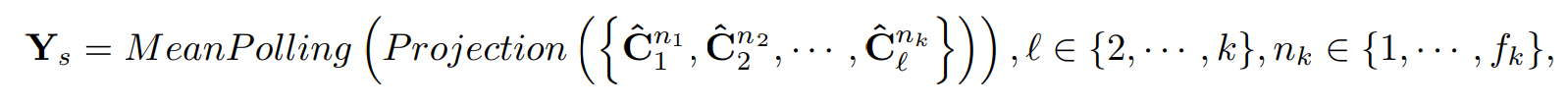
Trend part를 추가하고, de-normalization 을 통해 최종 아웃풋을 내게된다.

4 Experiment

4.1 Main Results

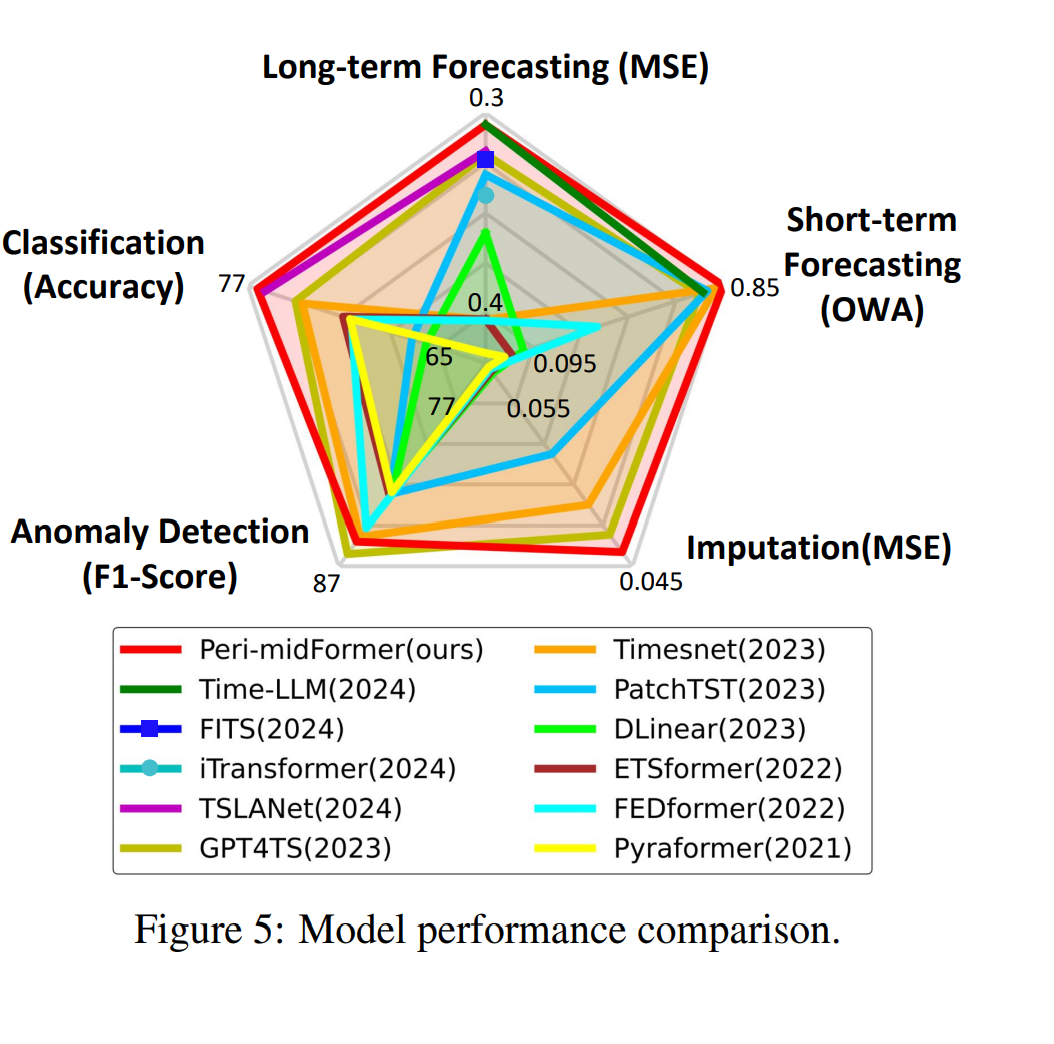
본 모델의 가지 시계열 태스크에 대한 퍼포먼스는 다음과 같다.

4.2 Long-term Forecasting

Setups

Weather, Traffic, Electricity, Exchange, ETT datasets (ETTh1, ETTh2,
ETTm1, ETTm2) 을 사용하여, 96, 192, 336, 720 스텝을 예측하였다.
비교의 공정성을 위해서 look-back 윈도우를 512로 (Exchange에서는 64)로 두었다.

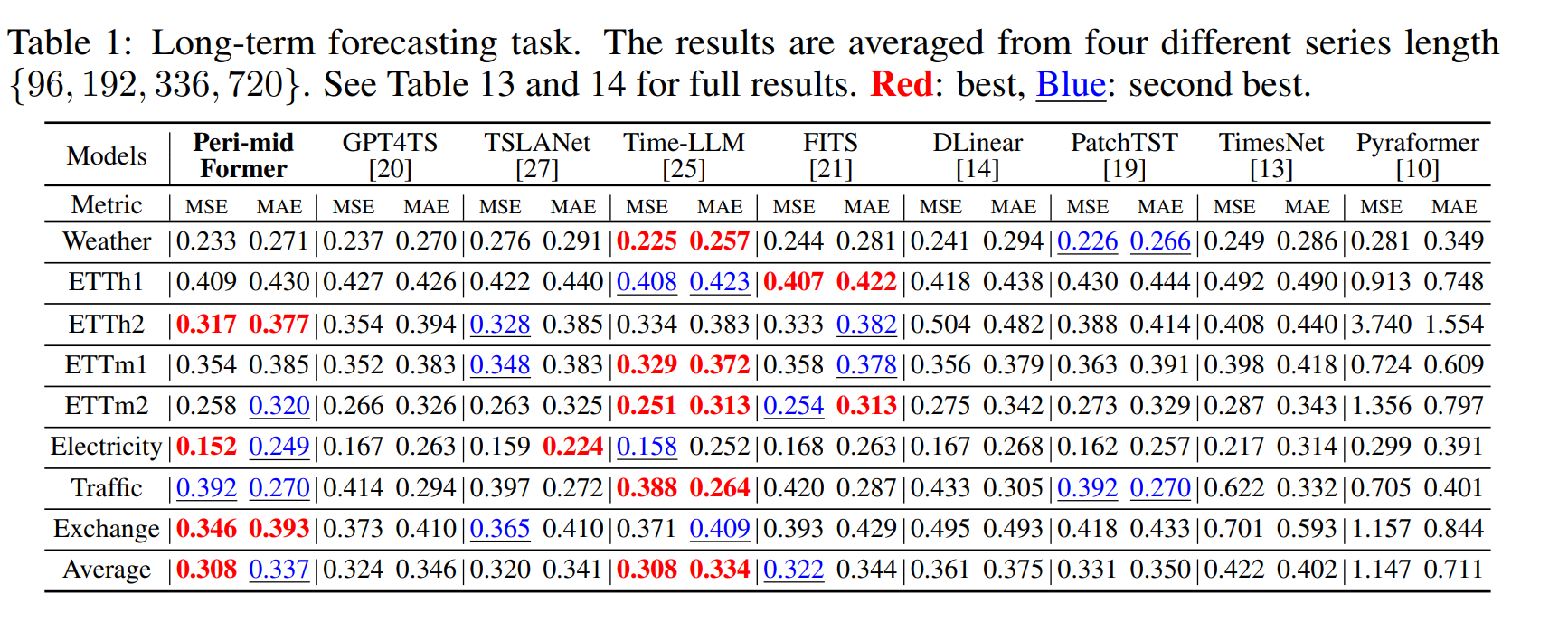
Results

Peri-midFormer 가 GPT4TS 대비 좋은 성능을 보였고, Time-LLM과 같은 SOTA 방법론과 비슷한 수치를 보였다. Time-LLM이 제일 좋은 성능을 보였더라도, 아주 헤비한 모델에 의존하였고, 너무 높은 코스트를 요구하는데 ㅂ받아, 우리의 방법론은 이러한 문제 없이 실제 어플리케이션에서 유용하다.

4.3 Short-term Forecasting

Setups

M4 데이터를 사용하였다. SMAPE, MASE, OWA 매트릭을 활용하였다.

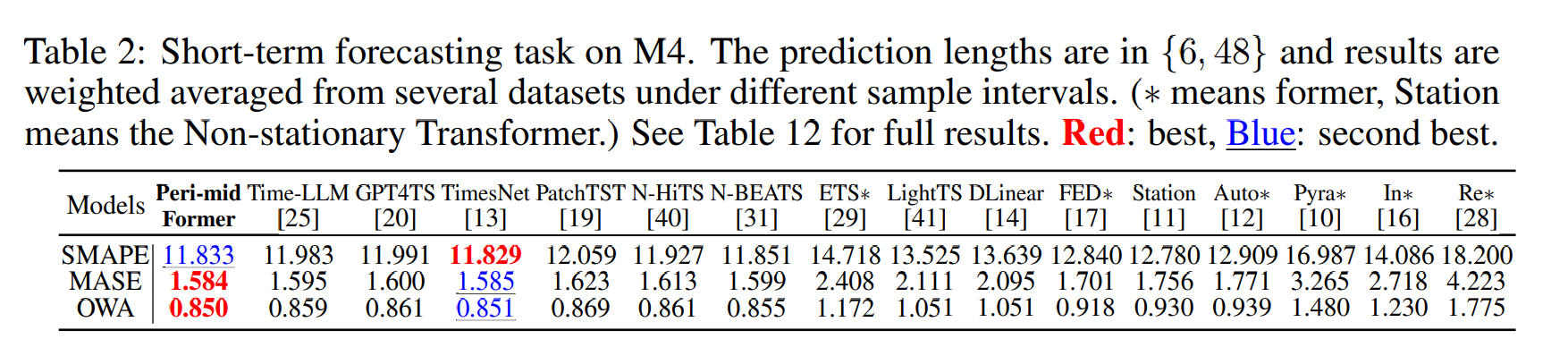
결과를 보면 Time-LLM, GPT4TS, TimesNet, N-BEATS에 비교하여 SOTA 성능을 달성하였다.

4.4 Time Series Classification

Setups

10개의 다변량 UEA classification 태스크를 통해 테스트하였다.

Results

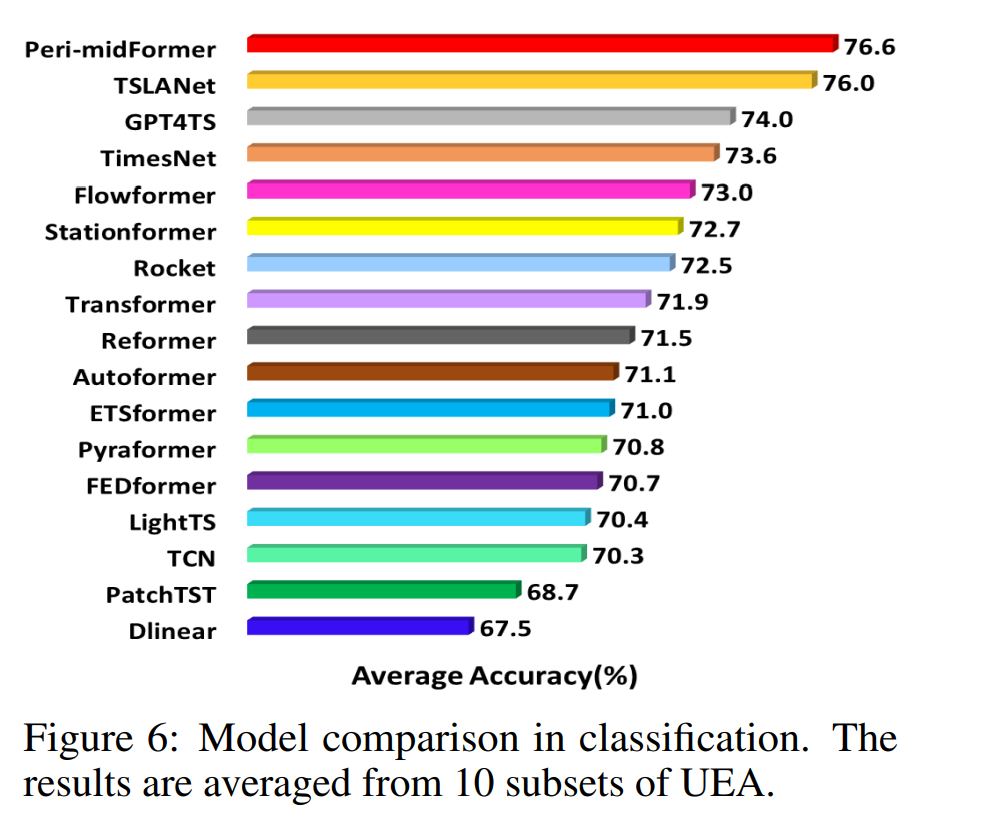
Peri-midFormer가 시계열 representation에서 효과적임을 보였다.

4.5 Imputation

Setups

ETT datasets (ETTh1, ETTh2, ETTm1, ETTm2),Electricity, Weather을 사용하였다.
마스킹 비율을 12.5%, 25%, 37.5%, 50% 로 각 두고 재ㅗㄱ원에 대한 정확도를 평가하였다.

Results

정확도가 SOTA 방법론에 근접함을 확인할 수 있다.

4.6 Time Series Anomaly Detection

Setups

SMD, MSL,SMAP, SWaT, PSM 데이터를 통해 모델을 평가하였다. 정상으로 학습한 뒤, 비정상 데이터가 들어왔을 때 재복원오차를 통해 확인하였다. PA를 적용하여서 정확도를 비교하였다.

Results

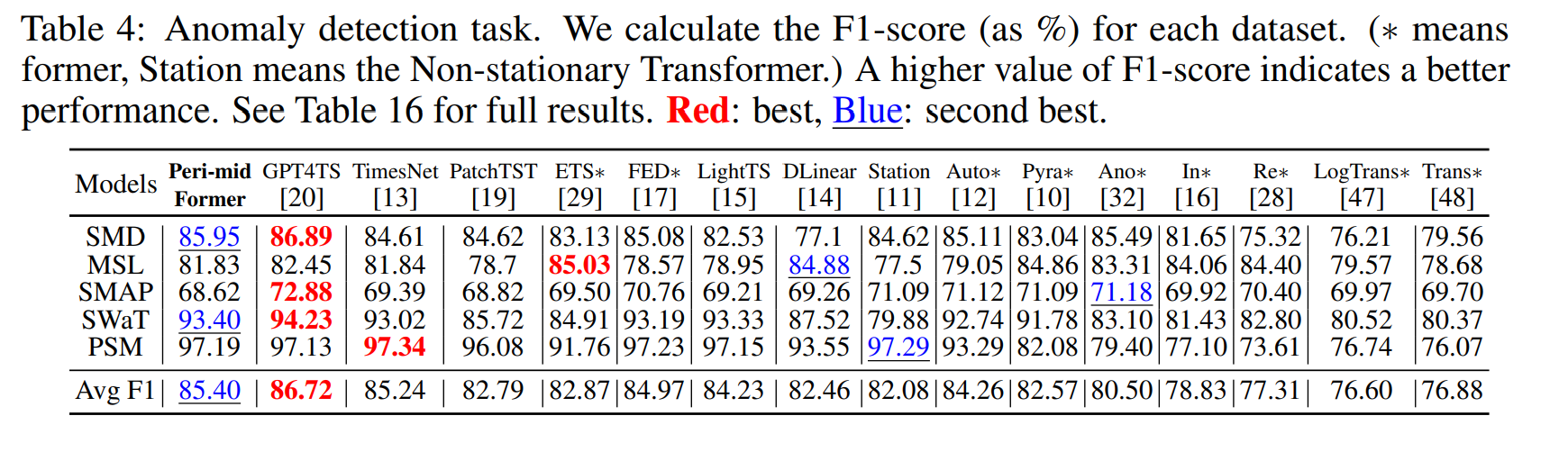
GPT4TS에 비해 2번째 성능을 달성하였다. 하지만 큰 갭이 있지는 않으며, 이는 AD dataset이 0또는 1을 가지는 데이터기때문에 유용한 주기 특성을 찾기 어렵게 만들었을 가능성이 높다.

5 Ablations

Setups

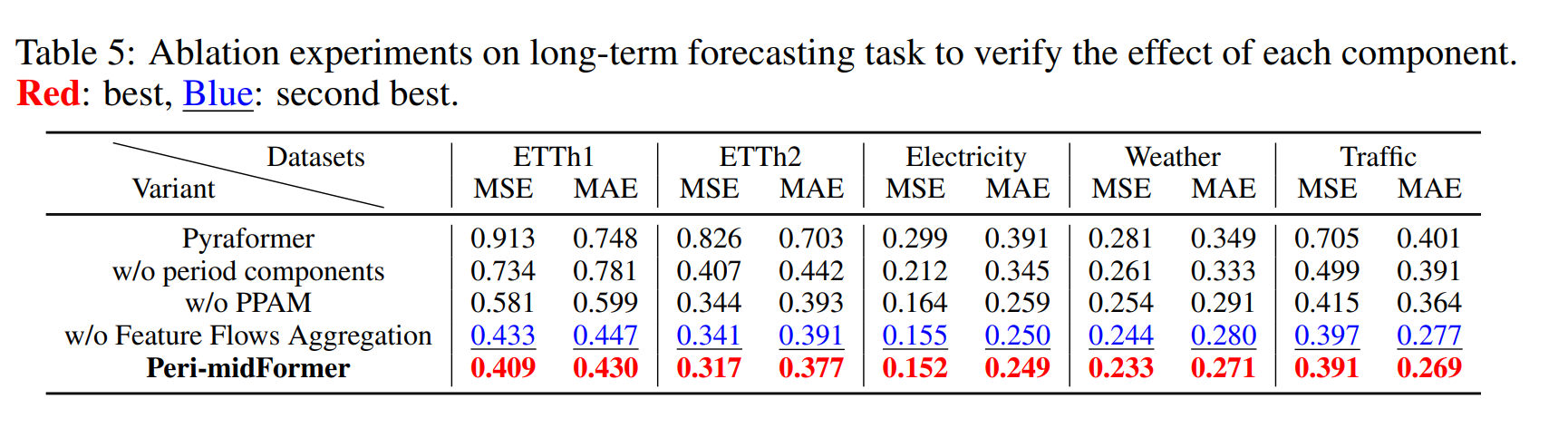
long-term 예측 태스크에서 다음과 같이 키 모듈에 대한 ablation 실험을 수행하였다.

Results

각 추가 모듈에 대한 실험을 통해 Peri-midFormer가 좋은 성능을 보임을 알 수 있다. 심지어 PPAM 없이도 좋은 결과를 보임을 알 수 있다. 이는 시계열에 내제된 주기적 성질을 추출하는 기본 적 특성 때문이다. 그러나 PPAM 으로 포함 관계를 강조하지 않은 경우에, 주기적 full 어탠션의 능력이 제한되어 성능이 떨어지게 된다.

6 Complexity Analysis

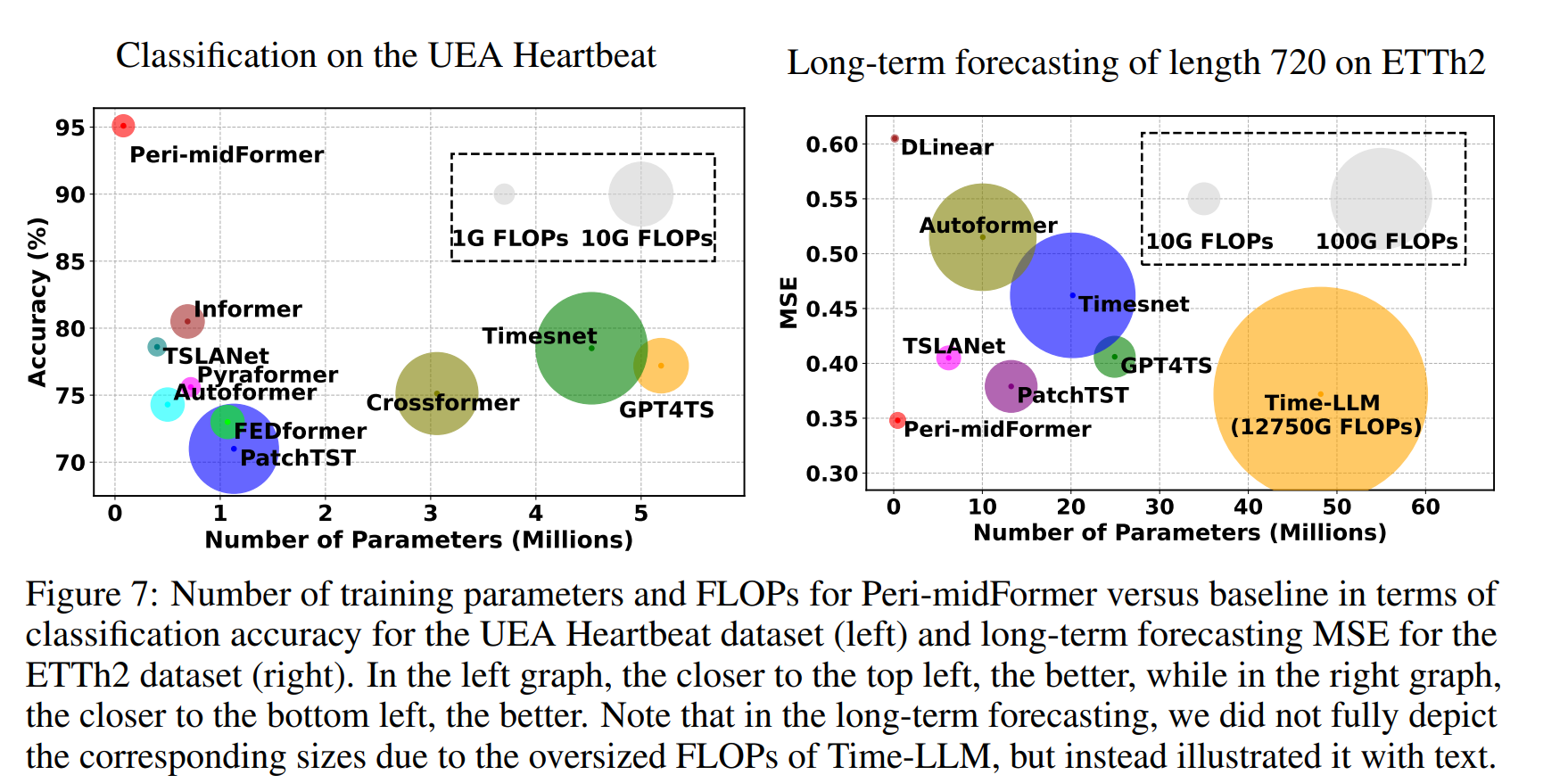
Peri-midForemr는 정확도 뿐만이 아니라 FLOPs에서 이점을 보였다.

Conclusions

본 연구에서는 시계열 분석 태스크에서 Peri-midFormer를 제안하였다. 이는 시계얼의 다양한 주기성과 포함 관계를 활용하였다. 원본 시계열을 다양한 레벨의 주기 컴포넌트로 segment하여 주기 피라미드를 attention 매커니즘을 통해 구축하여싿. 이는 예측, 분류, 임퓨테이션, 이상탐지 태스크에서 SOTA 성능을 달성하였고, 제안방법론의 효과를 입증하였다. 그러나,주기 특성이 분명하지 않은 시나리오에서는 한계점을 보였다. 이러한 한계점을 추후 연구에서 다룰 것이다.