[Network] HTTPS 암호화에 대하여(대칭키, 공개키)

yourjin·2022년 5월 26일

dev.log

목록 보기

5/14

➕ Topic

이 글은 HTTPS의 동작 원리를 이해하기 위해 알아두어야 할 암호화 지식들을 다룬다.

처음 HTTPS에 대해 공부하면서 어렵지 않게 이해했다고 생각했고, 누가 물어보면 잘 답변할 수 있을 것이라고 생각했는데 막상 닥쳐보니 그렇지 않았다.

HTTPS의 동작 과정은 나에게 일종의 암기처럼 느껴져서, 공부한 직후에는 이해가 되지만 시간이 지나면 까먹는 존재였다. 그리고 그 원인은 “암호화에 대해서 제대로 이해하지 못해서” 라는 생각이 들었다. 그래서 HTTPS를 다루기 전, 먼저 암호화에 대해 궁금했던 점들을 정리해보려고 한다.

이 포스팅을 통해 해결하고자 하는 궁금증은 다음과 같다.

대칭키 방식
- 대칭키는 어떻게 단점을 극복하고 많은 곳에서 사용되는가
공개키 방식
- 암호화 키와 복호화 키가 달라도 해독이 가능한 이유
- 공개키 암호화와 전자 서명의 차이
- 공개키는 왜 공개해도 되는가?
- 공개키 방식은 왜 대칭키 방식보다 느린가?

➕ Contents

암호화란?

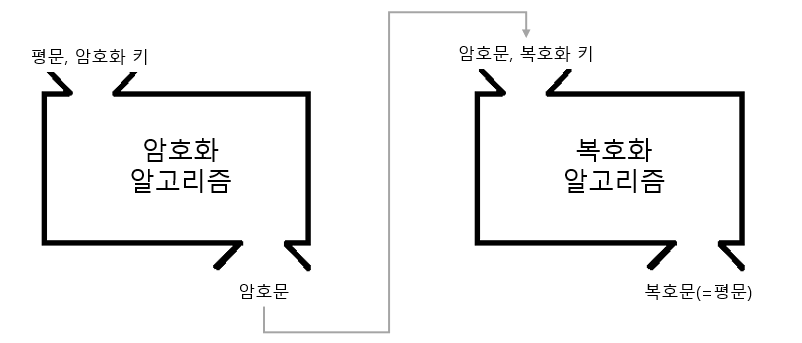
암호화는 암호화 알고리즘과 암호화 키를 이용해서 데이터를 남들이 해석할 수 없도록 만드는 것이다. 암호화 알고리즘은 공개되어 있다. 따라서 암호화에서는 사용되는 키를 어떻게 생성하고 관리하느냐가 핵심이라고 볼 수 있다.

암호화 기법에는 크게 대칭키 방식과 공개키(비대칭키) 방식이 있다.

🔑 대칭키(Symmetric Key) 방식

대칭키 방식은 암호화 키와 복호화 키가 같은 방식을 말한다.

암호화와 복호화 키가 같기 때문에, 복호화 하는 쪽에 비밀리에 키를 전달해줘야 한다.

이때 키를 보내지 않으면 복호화를 할 수 없고, 키를 보내면 도중에 탈취될 가능성이 있는데 이를 키 배송 문제(key distribution problem)라고 한다.

키 배송 문제는 다음과 같은 방법으로 해결할 수 있다.

키의 사전 공유에 의한 해결

사전에 키를 안전한 방법으로 서로 공유하는 방식이다.
송신자 A의 비밀 키를 수신자 B에게 전달하여, B에서 복호화가 가능하게 한다.
문제점
- 공격자가 중간에 가로챌 위험이 있다.
- 사용자가 많아지면, 그만큼 많은 키를 관리해야 한다.
  (이때 키 관리는 송신자, 수신자가 별도로 해야 한다.)

키 배포 센터에 의한 해결

키 관리를 송신자, 수신자가 별도로 하는 것이 아닌, 키 배포 센터(KDC, Key Distribution Center)라는 신뢰 받는 제 3의 기관에서 하는 것이다.
송신자 A의 비밀키를 수신자 B에게 전달하는 방식이 아니라, 키 배포 센터에서 한번의 통신만을 위해 생성한 세션키를 이용해 데이터를 암호화한다.
키 배포 센터에서 난수 생성기로 세션키를 생성하고, A, B의 각각의 비밀키로 이를 암호화해서 전달한다. A, B는 각각의 비밀키로 세션키를 알아내고, 이를 통해 데이터를 암호화하여 전송한다.
통신이 완료되면 송신자, 수신자 모두 세션키를 삭제한다.
문제점
- 사용자가 많아지면, 키 배포 센터가 그만큼 많은 키를 관리해야 해서 부하가 크다.
- 키 배포 센터에 문제가 생기면, 전체 암호화 통신에 문제가 생긴다.

Diffie-Hellman 키 교환에 의한 해결

자세한 동작 방식은 이 글에서 확인할 수 있다.

암호화에 사용할 비밀 키를 공개키 방식의 개념을 참고하여, 수학적 연산을 통해 생성해서 사용하는 방식이다.
송신자와 수신자 사이의 비밀 키가 이미 정해져서 이를 전달하는 방식이 아니라, 공개된 변수와 각자가 가지고 있는 비밀 변수들의 연산으로 만들어진 값을 비밀 키로 사용하는 방식이다. Diffie-Hellman key agreement(키 합의)라고도 한다.
이산 로그 문제(DLP, Discrete Logarithm Problem)가 해결하기 어렵다는 사실을 기반으로 한다.
- 컴퓨터 연산에서 지수 계산은 짧은 시간에 답이 나오지만, 로그 계산은 시간이 길게 걸린다.
간단하게 동작하는 방식을 그려보면 다음과 같다.
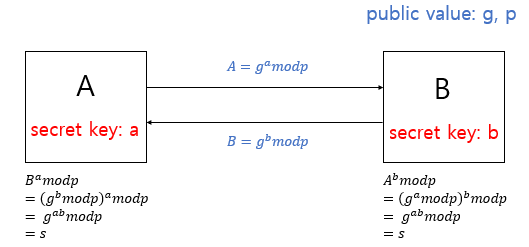
- A와 B는 각자 비밀 키 a, b를 가진다.
- 공개된 값 g, p를 이용해 연산한 값을 서로에게 전달한다.
- 전달 받은 값을 각각의 비밀 키와 연산하면 공통의 키 s를 구할 수 있다. (이를 이용해 데이터를 암호화한다.)
Diffie-Hellman 키 교환에서는 p가 충분히 크다면, 비밀 키인 a, b 값을 모르는 이상 A $(=g^b)$ 와 B $(=g^b)$ 값을 가지고 s $(=(g^a)^bmodp)$ 를 구할 수 없다.
- 만약 p가 최소 100자리 이상의 소수이고, a, b가 100자리 이상의 정수일 경우, 현재 인류가 보유한 모든 컴퓨터를 동원해도 공개된 정보로부터 비밀키를 알아낼 수 없다.
문제점
- 공개된 숫자가 너무 작은 경우, 비밀 키를 계산해낼 수 있다.
- 중간에 인증 과정이 없기 때문에 중간자 공격(man-in-the-middle attack)에 취약하다.

공개키 암호에 의한 해결

암호화 키와 복호화 키가 다른 공개키(비대칭 키) 암호화 방식을 사용한다.

🔑 공개키(Public Key) 방식

공개키 방식은 (공개키, 개인키)가 하나의 묶음으로 동작한다. 즉, 공개키로 암호화를 하면 개인키로만 복호화할 수 있고, 개인키로 암호화하면 공개키로만 복호화할 수 있다.

어떤 키로 암호화 하느냐에 따라 크게 공개키 암호화와 전자 서명(인증)으로 구분한다.

공개키 암호화와 전자 서명

공개키 암호화는 말 그대로 공개키로 암호화하고, 복호화는 개인키로만 가능한 방법이다. 복호화가 개인키로만 가능하기 때문에, 데이터가 보호되어야 할 때 사용된다.

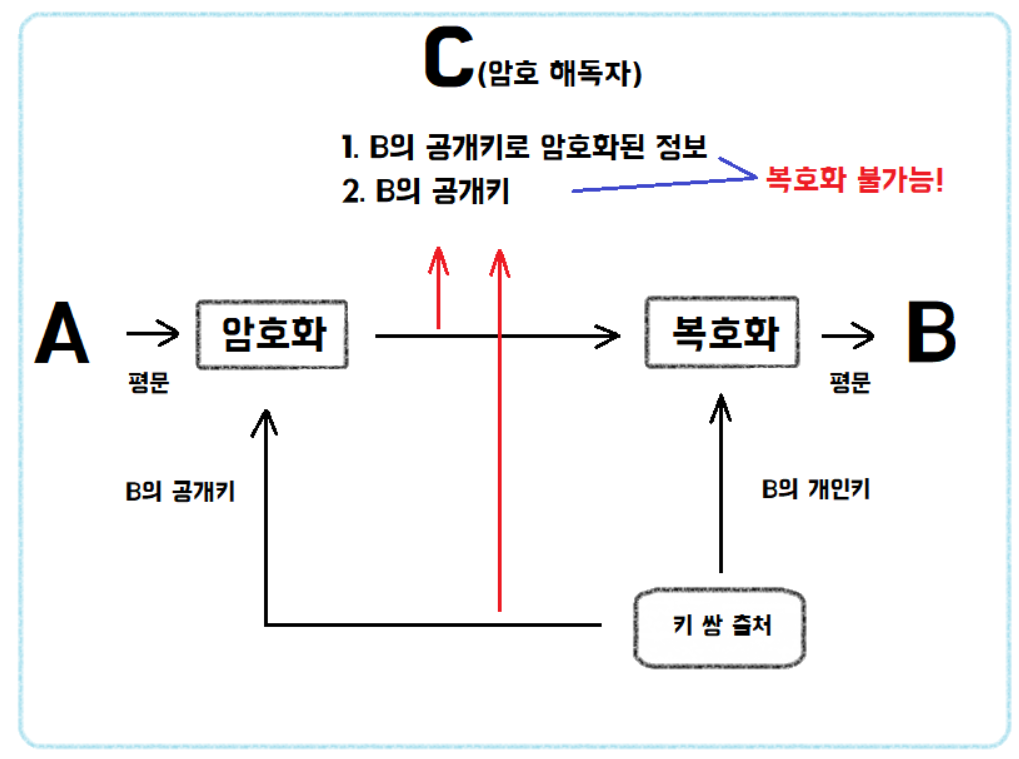
전자 서명은 반대로 개인키로 암호화하는 방식이다. 따라서 공개키로 복호화가 가능하다. 즉, 나의 개인키에 대한 공개키를 알고 있는 사람이라면 누구나 복호화할 수 있다. 당연히 보안이 중요한 데이터는 이 방법으로 암호화하면 안된다. 대신 이 데이터를 보낸 사람이 나라는 것을 증명(인증)할 수 있다. 공개키와 개인키는 쌍으로 동작하기 때문에, 특정 공개키로 복호화 가능하다는 것은 해당 공개키의 쌍인 개인키로 암호화되었다는 것을 의미한다. 이 특성을 이용해 사용자를 인증하는 데 사용할 수 있다.

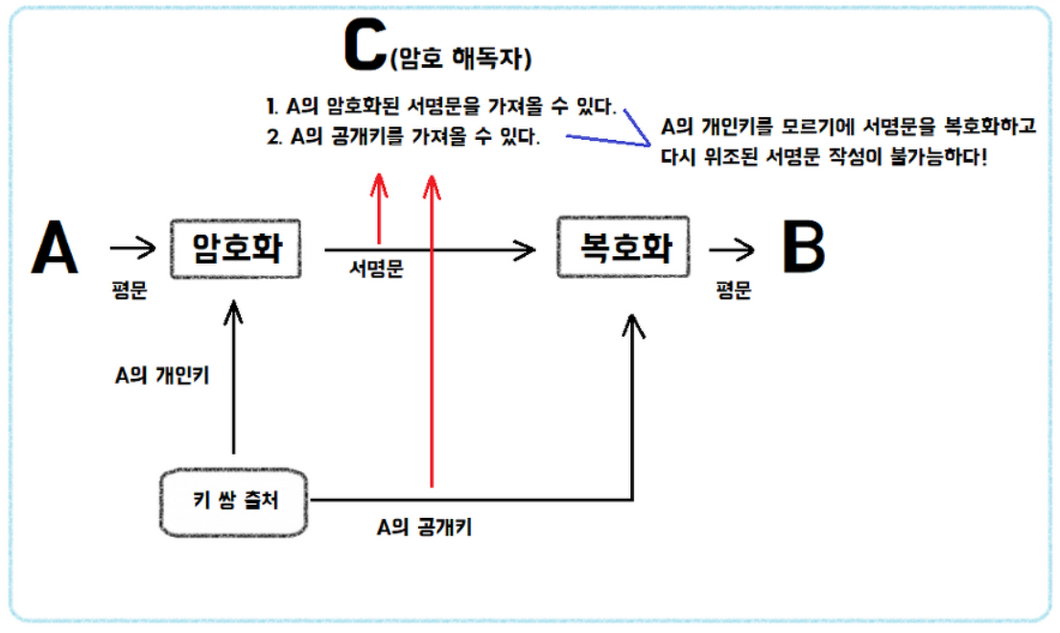
간단하게 살펴 보는 RSA 알고리즘

RSA 알고리즘에 대한 자세한 설명은 이 글에서 확인할 수 있다.

RSA는 공개키 방식에서 대표적으로 사용되는 알고리즘 중 하나이다. RSA는 복잡한 수학적 연산을 통해 사용 가능한 (공개키, 개인키) 묶음을 만들어주는 알고리즘이라고 생각하면 편하다. RSA 암호는 2개의 큰 소수를 곱하는 것은 쉽지만, 곱해진 결과가 어떤 두 소수의 곱 인지 알아내는 것은 어렵다는 성질을 이용한다.

RSA에서 키를 만드는 방법은 다음과 같다.

큰 소수 p, q를 준비한다.
p-1, q-1 모두와 서로소인 e를 준비한다.
- 오일러 공식에 따라 $N = p * q$ 일 때, $\varphi(N) =(p-1) *(q-1)$ 이다.
- $\varphi(N)$ 은 오일러-phi 함수로, 1부터 N까지의 수들 중에서 N과 서로소인 수들의 개수이다.
ed가 (p-1) (q-1)로 나눈 나머지가 1인 d를 찾는다.
이제 N과 e는 공개되고, e는 공개키 d는 개인키로 사용한다.

이런 식으로 만든 공개키 e로 암호화하면, 개인키 d를 사용해 복호화하여 원래 문장을 찾을 수 있다. 암호화 키와 복호화 키가 달라도 되는 이유는 e*d(modN)이 1인 성질을 가지기 때문이다.

송신자 A는 평문 a를 공개키 e로 암호화한 x값을 수신자 B에게 보낸다.
- $x = a^emod(N)$
수신자 B는 암호문 x를 개인키 d를 통해서 복호화한다.
- $x^dmod(N) = (a^emod(N))^dmod(N) = (a^e)^dmod(N) = a$

N과 e를 공개해도 되는 이유에 대해 생각해보자. 복호화 키 d를 구하기 위해서는 N을 구성하는 소수 p, q를 알아야 한다. 그래야 p-1, q-1과 서로소인 e를 통해 d를 구할 수 있기 때문이다. N이 작을 경우 p, q를 구하는 소인수분해 과정은 어렵지 않다. 가장 쉬운 방식으로 루트 n보다 작은 값들을 일일이 나눠서 구하는 방식이 있다. 하지만 우리가 암호화에 사용하는 소수 p, q는 굉장히 큰 수이다. 이를 소인수분해하여 p, q를 구하는 것은 물리적, 시간적으로 어렵다. 따라서 현실적으로 개인키인 e를 구할 수 없다고 판단한다.

예를 들어 30자리 수를 소인수분해하기 위해 10^15보다 작은 수로 나누어보면 되는데, 1초에 100만 번 연산을 수행하는 슈퍼컴퓨터라 할지라도 계산하는 데 10^9초가 소요되므로 약 30년이 걸린다.

마지막으로 우리가 암호화, 복호화에서 사용한 $x = a^emod(N)$ 연산의 시간 복잡도에 대해서 생각해보자. 지수 연산에서는 밑의 수를 n번 만큼 곱해주면 되기 때문에, 시간 복잡도는 $O(n)$ 으로 볼 수 있다. 이전에 구한 값을 저장해두고 어느 수의 제곱을 구할 때 이를 사용한다면, 시간 복잡도를 $O(logn)$ 까지 줄일 수 있다. 하지만 RSA에서 사용되는 키 값은 매우 크기 때문에, 지수 연산을 하는데도 상당한 시간이 소요된다고 한다. 그래서 RSA 만으로 모든 암호화를 하지는 못하고, 다른 암호화 방식이랑 연동하여 쓰는 것이 보통이라고 한다.

공개키는 왜 공개해도 되는가?

결론부터 말하자면, 암호화한 공개키를 공개해도 복호화를 위한 개인키를 구하는 데 시간이 너무 오래 걸려 현실적으로 찾을 수 없다고 판단하기 때문이다. RSA 알고리즘에서 간단하게 살펴봤듯이, 매우 큰 숫자를 소인수분해해서 그 중에 키 값을 도출하는데 사용하는 값을 알아내는 것은 어렵다.

공개된 정보로 개인키를 찾기 위해서는 대체로 NP(Non-deterministic Polynomia)와 같이 여러가지 가능성을 동시에 고려해야 해서 연산이 어려운 문제를 해결해야 한다.

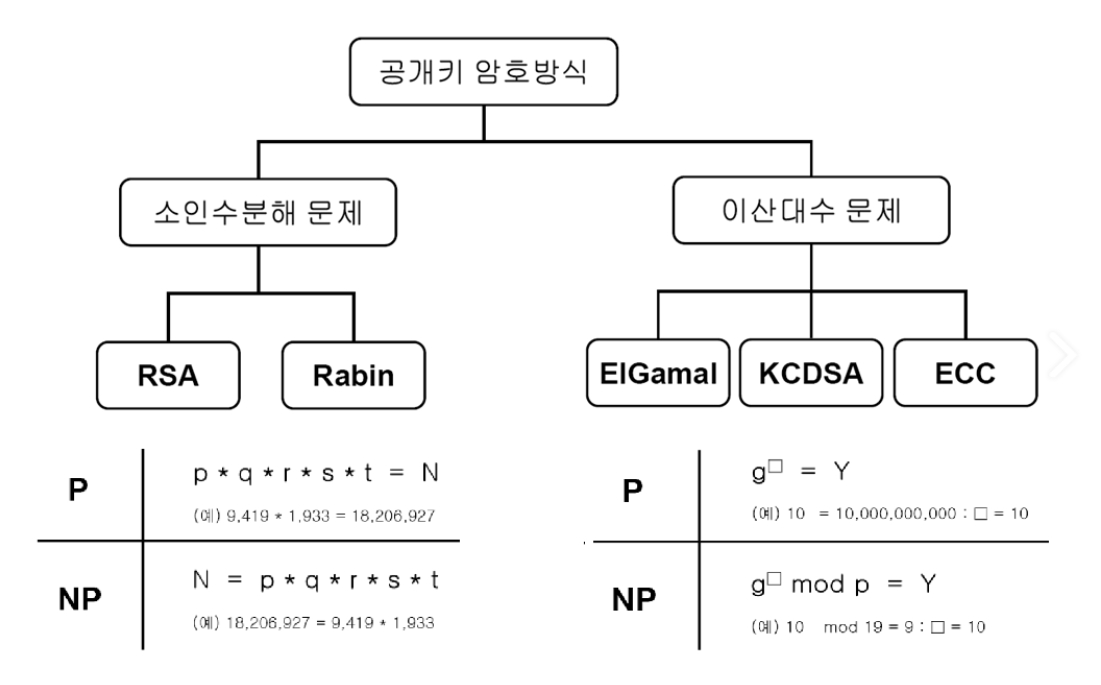
공개키는 왜 대칭키보다 느린가?

이것도 RSA 알고리즘에서 살펴본 내용을 참고하면 이해하기 수월해진다. 공개키 방식은 개인키를 제3자가 구할 수 없게 하기 위해 키 값을 매우 크게 사용하는 것이 보통이다. 그리고 암호화, 복호화 알고리즘에서 이 키를 가지고 연산하기 때문에 그만큼 연산량이 많다. 즉, 공개키는 키로 사용되는 값이 매우 커서 이를 가지고 암호화, 복호화 연산을 하는데 시간이 많이 소요된다.

그에 비해 대칭키는 키를 비밀로 관리하기 때문에, 키 배송 문제만 없다면 공개키 방식만큼 키 값이 클 필요가 없다.

결론

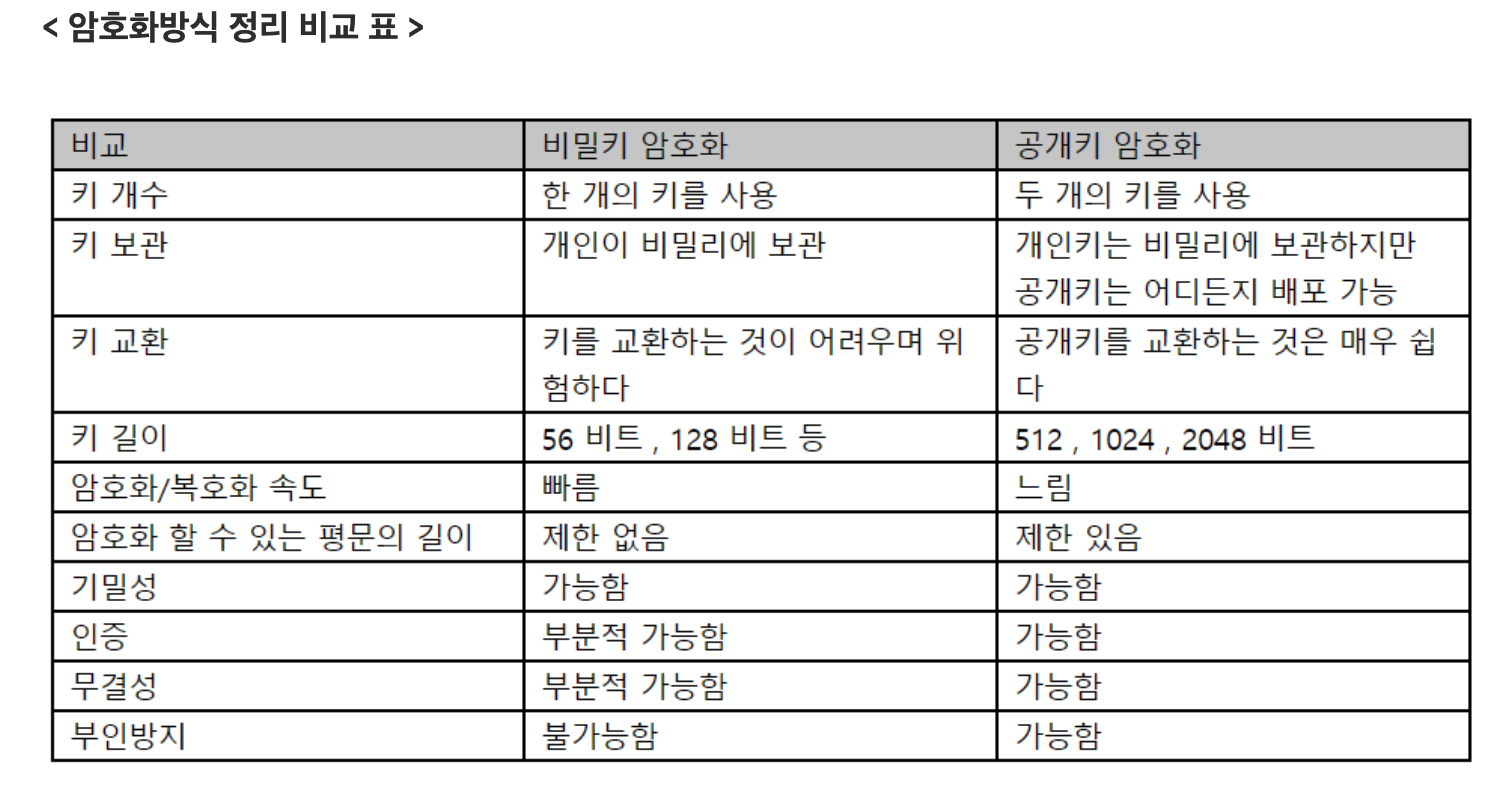
흔히 암호화를 공부하다보면 위와 같은 표를 볼 수 있다. 앞선 내용들을 다루고 보니, 이런 특징들이 더 잘 이해가 되는 것 같다. 마지막으로 궁금증에 대한 요약 정리로 포스팅을 마치도록 하겠다.

대칭키는 어떻게 단점을 극복하고 많은 곳에서 사용되는가
- 대칭키 방식은 공개키 방식에 비해 암호화, 복호화 속도가 빠르다. 이런 장점을 살려 실제로는 대칭키 방식과 공개키 방식을 혼합하여 사용하는 경우가 많다고 한다.
암호화 키와 복호화 키가 달라도 해독이 가능한 이유
- 암호화 키로 연산하고, 복호화 키로 연산하면 결과적으로 원래 데이터가 나오도록 수학적으로 설계가 되어있기 때문이다.
공개키 암호화와 전자 서명의 차이
- 공개키 암호화는 복호화를 개인키로만 할 수 있기 때문에 데이터의 기밀성이 보장된다.
- 전자서명은 복호화를 공개키로 할 수 있기 때문에 데이터의 기밀성은 보장되지 않지만, 해당 공개키와 쌍을 이루는 개인키로 암호화된 내용이라는 것을 확인할 수 있다는 점에서 보낸 사람을 증명할 수 있다.
공개키는 왜 공개해도 되는가?
- 공개된 정보를 가지고 복호화에 필요한 개인키를 (현실적으로) 찾을 수 없다고 판단하기 때문이다. 개인키를 알기 위해서는 수많은 경우의 수에 대입해봐야 하기 때문이다.
공개키 방식은 왜 대칭키 방식보다 느린가?
- 공개키 방식은 키에 사용되는 값이 매우 크다. 따라서 이 키를 사용해 암호화, 복호화 연산에 드는 시간이 그만큼 많이 든다.