인덱스

더 빠른 검색을 위해 특정 컬럼에 대하여 정렬하여 색인을 만들어 데이터의 저장위치를 빠르게 찾을 수 있도록 하는 것

아래 그림처럼 이름에 대해 인덱스를 생성하여 SMITH가 위치하는 레코드를 빠르게 찾을 수 있게 한다.

이러한 인덱스는 보통 B-Tree로 구성하게 된다.

B-Tree

B-Tree의 개념

• 좌우균형을 유지하는 트리로, 이진트리의 단점을 극복 가능
• 이진트리와 다르게 한 노드에 여러 key 저장 가능
• 최대자식노드 개수가 M개일 때, M차 b-tree라고 한다.

---

B-Tree의 특징

• 부모노드의 key의 개수+1 만큼 자식노드를 가져야함
• leaf노드는 모두 같은 레벨에 있다.
• 노드에 여러 key는 정렬되어 있다.
• 입력자료에 중복은 없다.

B-Tree는 다음의 3가지 키워드를 가진다.
균형잡힌, 다진트리, 외장검색트리

• 균형잡힌
  이진 탐색트리의 경우 균형이 한쪽으로 쏠리는 경우 최악의 탐색복잡도인 O(logN)을 가지게 된다. B-Tree는 왼쪽 서브트리와 오른쪽 서브트리의 균형을 유지하도록 하여 적정 깊이를 유지한다.
  

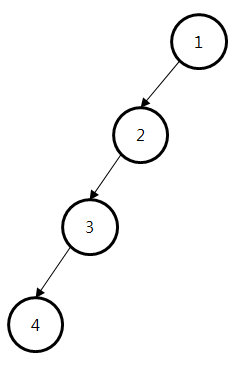
• 다진트리
  이진트리와 다르게 B-Tree는 하나의 노드에 여러 key를 담을 수 있다. 이러한 구조는 적은 depth를 가질 수 있도록 하며, 참조포인터를 거치는 횟수를 줄여준다. 최종적으로 디스크 접근 횟수를 줄이게 된다.
  
  

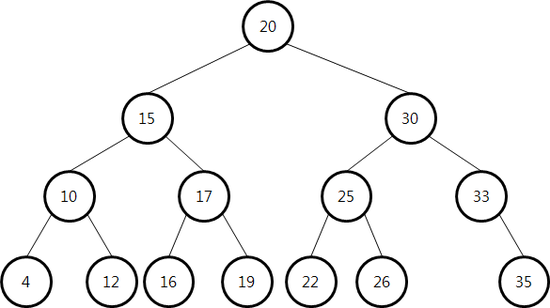
• 외장검색트리
  외장검색트리란 메모리가 아니라 디스크 상에 검색색인을 올려놓고 사용한다는 것이다. 메모리에 비해 디스크 접근은 매우 많은 비용을 소모한다. 따라서, 디스크 접근횟수를 줄일 수 있는 B-Tree의 특성은 외장검색트리에 적합하다.

그런데 실제론 이러한 B-Tree를 더욱 발전시킨 B+Tree를 사용한다.

B+Tree

B+Tree는 아래와 같은 특징을 가진다.

• 데이터의 저장을 leaf node에만 한다.
• leaf node끼리는 linked list로 연결되어 있다.
• leaf node에 모든 키와 데이터를 저장하고 leaf node의 키를 찾는데 윗단의 노드가 사용되기에 key의 중복이 있을 수 있다.

B+Tree의 장점

• leaf node에만 데이터를 저장하기에 내부 노드(leaf node가 아닌 모든 노드)에 더 많은 key를 저장하여 트리의 depth를 줄일 수 있다. 이는 검색 속도를 증가할 수 있다.

  B-Tree는 부모노드의 key개수+1 만큼의 자식 노드를 가진다는 특성이 있는데 depth를 줄일 수 있는가? 의문이 있었다.
  실제로 같은 차수의 b- b+ tree는 같은 depth를 갖는다. 위의 워딩은 더욱 높은 차수의 B+Tree를 만들 수 있다는 것이다.

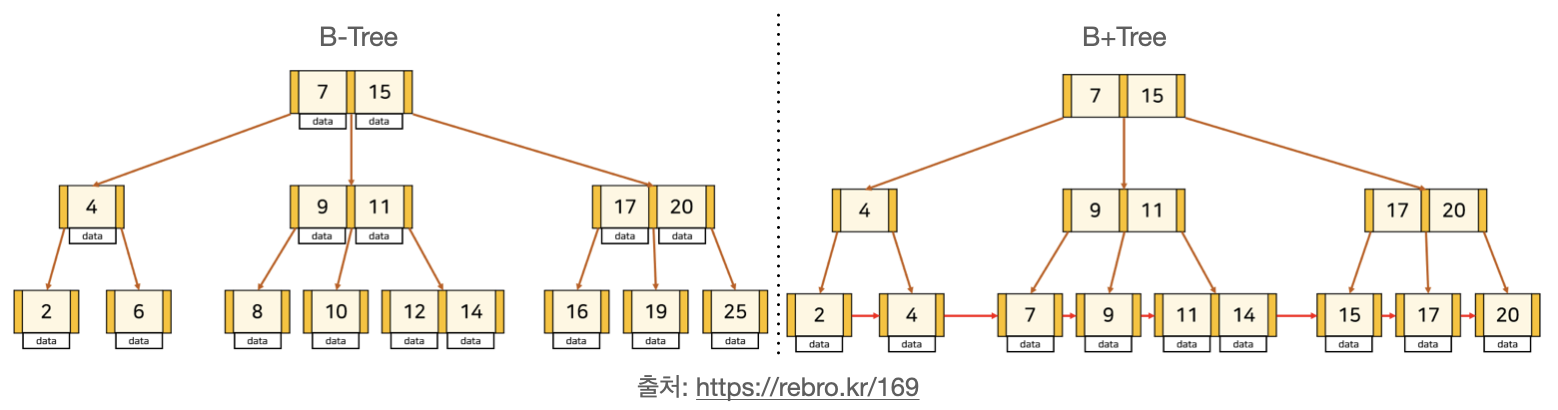
1~12가 들어있는 Max Degree 3인 B-Tree

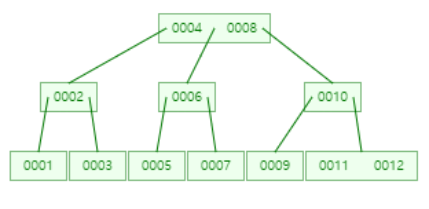
1~12가 들어있는 Max Degree 3인 B+Tree

같은 차수일 경우 오히려 B+Tree가 더욱 깊은 depth를 갖는다.

• Full scan을 하는 경우 B+Tree는 모든 데이터가 leaf node에 linked list로 되어 있어 leaf node만 순차 탐색하면 된다.
  반면 B-Tree는 모든 노드를 각각 검색 해야한다.

B+Tree의 단점

• 데이터를 찾기 위해 무조건 leaf node까지 내려가야 한다.

즉 하나의 데이터만 찾을 경우엔 B-Tree가 빠르지만 여러 순차데이터를 찾는 경우
linked list를 통해 순차적 검색을 할 수 있어 B+Tree가 인덱스에 사용된다.

인덱스 검색 과정

위의 개념을 이해할 때 혼동됐던 부분은 key와 데이터가 무엇을 나타내는 것이고, 실제 인덱스상에서 컬럼의 값과 레코드의 위치가 어떻게 저장되는 것인지였다.

B+Tree에서
key는 컬럼의 값을 의미한다.
데이터는 레코드의 위치를 의미한다.

특정 컬럼에 대한 질의가 들어왔을 때,
1. 우선 조건에 맞는 컬럼은 b+tree의 루트 노드부터 시작하여 하위노드로 내려가며 leaf node 어디에 해당 컬럼값(key)가 위치하는지 찾는다.

2, 리프 노드에 저장되어 있는 키 값과 해당하는 데이터의 포인터* 를 통해 실제 데이터가 저장된 블록 또는 디스크 주소 등을 찾는다.

포인터*
키 값과 연관된 데이터(레코드)의 물리적인 저장 위치를 가리키는 역할을 한다.

아래 그림에서도 내부 노드는 자식 노드의 주소를 가리키고 있고, 리프노드에서 레코드의 위치(primary key)를 가리키고 있다.

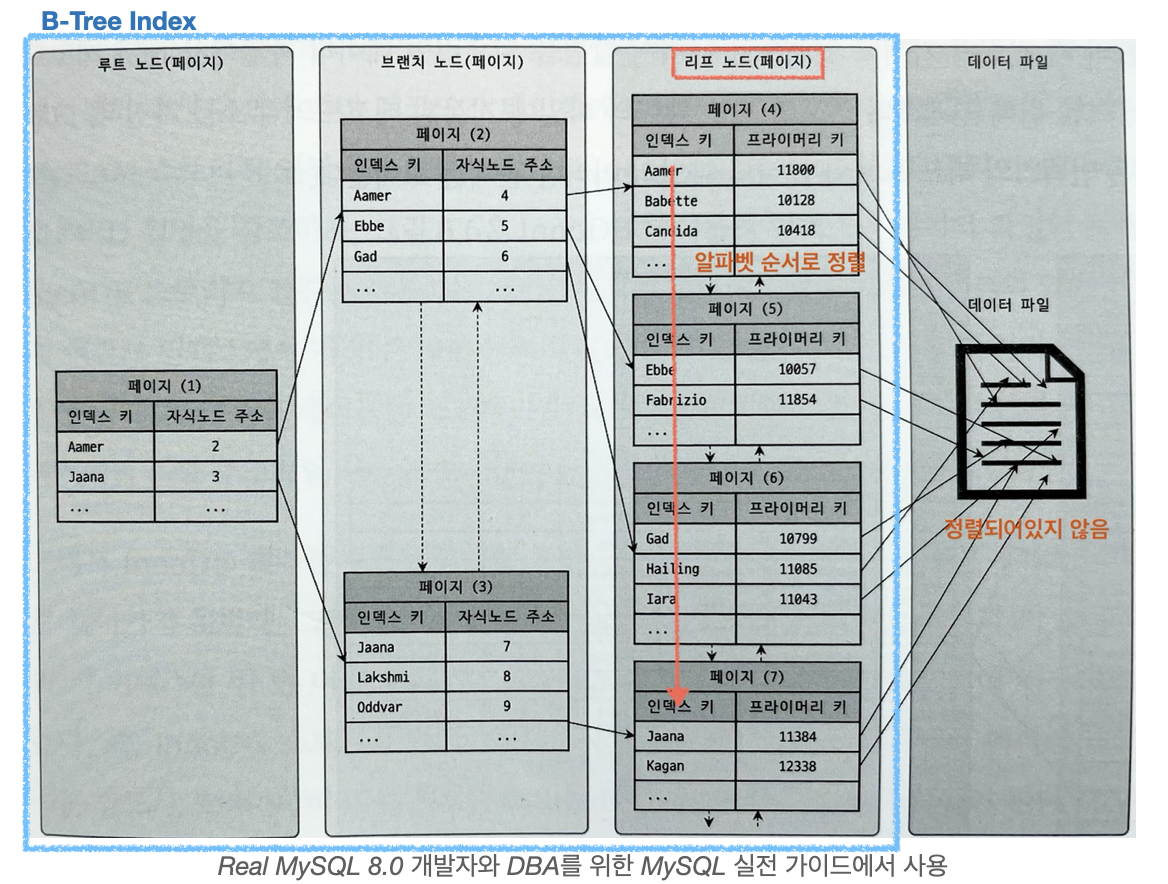
B-Tree vs B+Tree

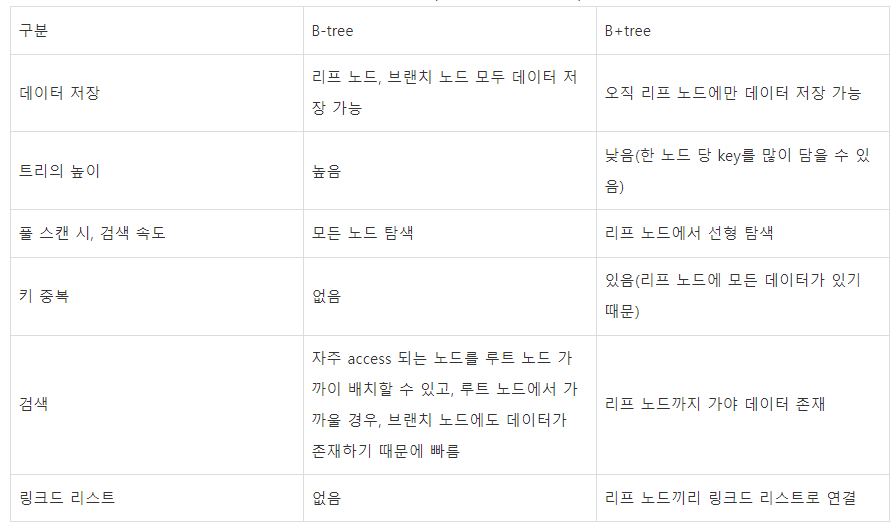
출처 : https://zorba91.tistory.com/293

다른 자료구조를 사용하지 않는 이유

그런데 b+tree의 liked list구조가 순차 검색을 더욱 빠르게 해준다면 그냥 array나 linked list를 사용하면 되는 것 아닌가? 하는 의문이 들 수 있다.

Array

array는 데이터의 물리적 논리적 위치가 같기에 접근이 매우 빠르다.

그렇기에 인덱스에 사용하면 key를 찾는 과정은 빠를 수 있다. 하지만 삽입 삭제시 매우 많은 cost가 든다. 데이터의 삽입/삭제가 일어날 시 순서를 유지하기 위해 주변 모든 데이터를 한꺼번에 shift해야하고, 이는 O(N)의 복잡도가 발생한다.

Linked List

그렇다면 삽입 삭제가 용이한 liked list는 어떨까?

liked list는 탐색시 반드시 head node부터 시작해야하고, 이는 탐색이 중요한 인덱스에 사용되기 어렵다.

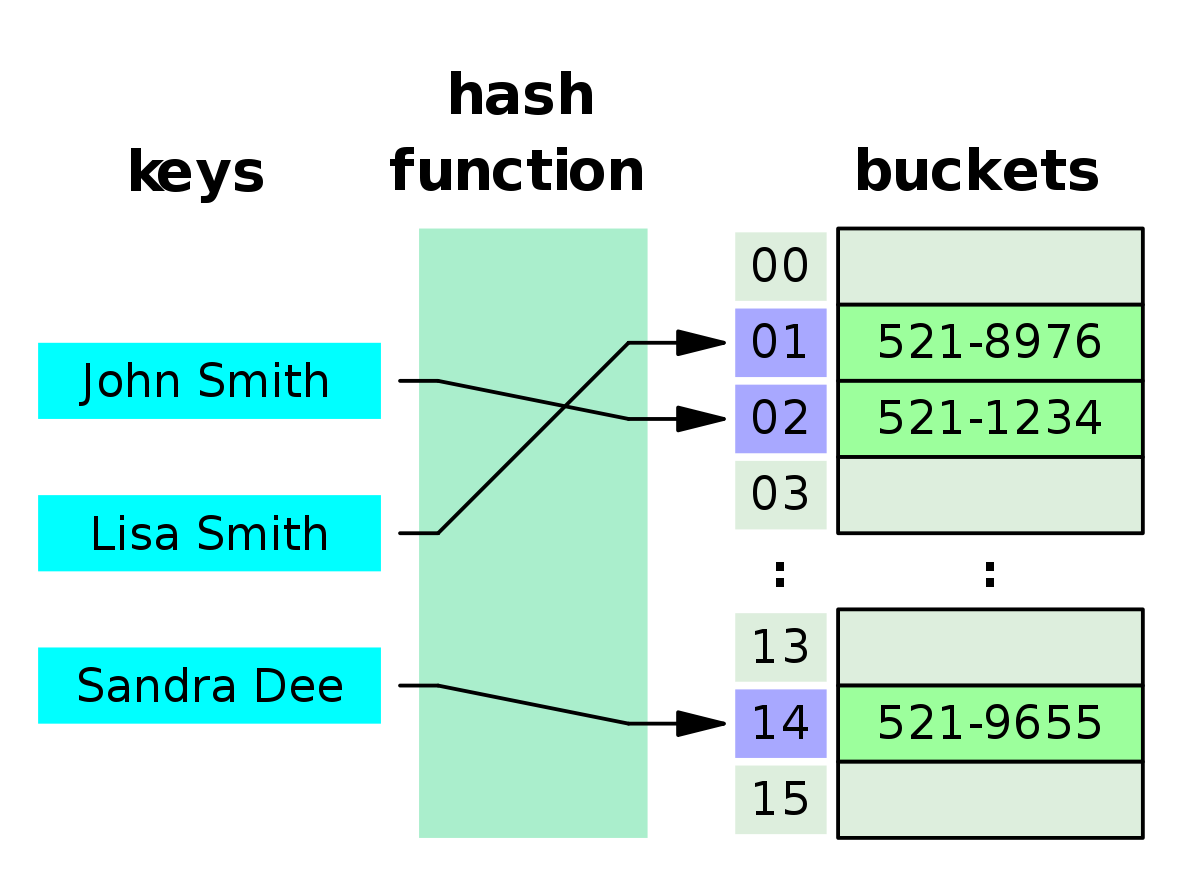
Hash

key:value형태의 hash는 탐색시간이 매우 빠르다. O(1)이다. 그러나 이는 '='쿼리에 대해서만이다. 부등호(<,>) 쿼리의 경우 탐색이 어렵다.

결론

B+Tree는 균형적인 다진 트리로서 필요 key를 탐색하기 좋고,
leaf node에 linked list로 모든 데이터가 연결되어 있어 여러 개의 순차적인 데이터를 탐색하는 데 적합하기에 부등호 연산이 많이 요구되는 인덱스의 자료구조로서 사용된다.

참고자료
https://rebro.kr/167
https://velog.io/@ann9902/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-b-tree

https://velog.io/@ann9902/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-b-tree%EB%A5%BC-%EC%99%9C-DB%EC%97%90-%EC%82%AC%EC%9A%A9%ED%95%A0%EA%B9%8C

https://helloinyong.tistory.com/296