activation function

Why?

1. 선형의 affine함수를 여러겹 쌓는다고 비선형의 데이터 분포를 근사할 수는 없다. 이때 중간마다 비선형의 활성화함수를 추가하여 비선형성을 추가해줄 수 있다.

2. affine 결과를 일정한 범위의 값으로 정제할 수 있다.

Q. 비선형의 affine layer를 사용한다면?
선형 affine layer + 다항식이 아닌 활성화함수 조합으로 임의의 함수 근사가 가능하다는 것이 증명됌

How?

sigmoid, tanh, relu, leaky relu등의 활성화 함수가 존재한다.

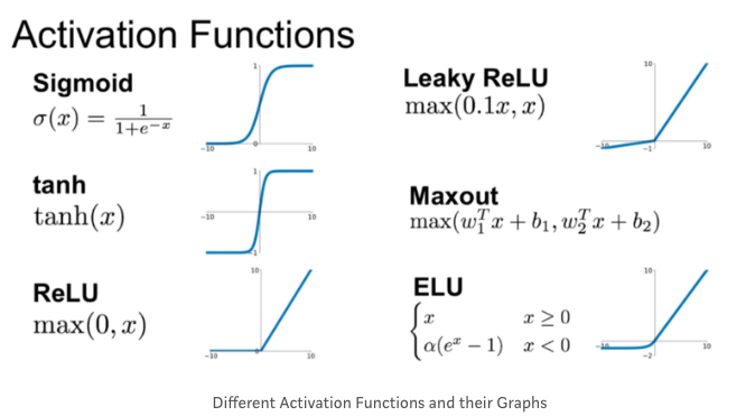
Gradient Vanishing

gradient vanishing은 대부분 활성화함수의 미분값으로 인해 야기되는데, sigmoid함수의 경우 미분값 그래프를 보면 최대값이 0.25로 역전파를 하며 0보다 작은 값을 곱하다보면 0에 가까워지는 문제가 발생하게 된다.

이를 막기위한 방법으로는

activation function 변경

relu를 사용할 경우 미분값이 1로 유지되기 때문에 완화될 수 있다. 그러나 음수의 경우 0이 되기 때문에 leaky relu를 사용하기도 한다.

가중치 초기화

활성화함수 결과값이 고르게 분포해야 학습이 원활하게 이뤄질 수 있다.

이를 위해선 가중치를 잘 설정하는 것이 중요하다.

Xavier 초기화

이전 레어의 노드 개수의 루트값의 역수를 표준편차로 하는 분포로 초기화

sigmoid, tanh 에 적합하다.

He 초기화

이전 레어의 노드 개수의 루트값의 역수의 두배를 표준편차로 하는 분포로 초기화

ReLU에 적합하다.

Q. 가중치를 모두 0으로 초기화한다면?
모든 가중치가 0이라면 순전파시 모든 노드의 값이 같아질 것이고 역전파 결과도 같아, 모두 같은 값으로 업데이트 될 것이다. 이는 서로 다른 가중치로 데이터의 특징을 파악해내야 하는데, 이것이 불가능해진다.

Batch Normalization

활성화함수결과값이 고르게 분포하는 것이 좋다면 이를 강제하는 방법은 어떨까?

이것이 바로 batch normalization이다.

Why?

internal covariate shift 문제를 완화할 수 있다.
이는 매 레이어를 거치면서 입력의 분포가 달라지는 문제를 말한다.

What?

활성화 함수 입력전에 배치의 평균과 분산으로 정규화하는 것이다.
scale과 shift를 담당하는 파라미터가 존재하고 backprop시 학습된다.

구조적 변경

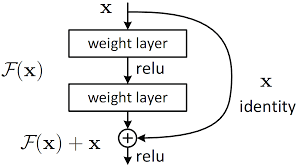
Residual network

x를 더해서 F(x)+x 형태로 다음 레이어에 넘겨서 F(x)에서 그래디언트가 작아져도 x를 통해 보존되게 된다.

RNN -> LSTM

LSTM에서는 Cell state를 도입해서 그래디언트가 흐를 수 있는 독자적인 루트를 마련해서 그래디언트를 보존할 수 있게 한다.