MIPS Format (R/I/J)
MIPS 5 stage pipeline (IF-ID-EX-MEM-WB)
Hazards
1. Structural Hazard : add more HW resources
2. Data Hazard : forwarding & compiler scheduling
3. Control Hazard : delay slot & prediction
[MIPS란?]
-
MIPS는 전형적인 RISC ISA이다.
-
MIPS는 고정된 길이(32bits)와 형식(R/I/J)을 갖는다.
32bits 기준으로 0~31까지 32개의 register가 존재한다. -
MIPS는 모든 명령어들에 대해 3개의 operands를 가진다.
-
MIPS instructions는 register-register arithmetic instruction이다. 즉, 메모리에 액세스하기 위해서는 무조건 register로 데이터를 가져온다. 연산 후에는 결과를 메모리에 저장하는 구조로 동작한다. (메모리에 대고 직접 연산하는 경우는 존재하지 않는다.)
-
load/store machine이라고 불리기도 한다.
(이는 모든 작업을 메모리로부터 load → 연산 → 메모리에 store하는 구조로 동작하기 때문이다.)
[MIPS Format]
: MIPS instruction은 오직 3가지 format만을 갖는다.
R format
-
Register-Register 연산에 해당한다. (일반적으로 산술 연산)
-
3개의 register를 사용한다.
- rd: destination register
- rs: first source register
- rt: second source register
-
add, sub와 같은 명령어들이 있다.

I format
-
Register-Immediate과 conditional Branch 연산에 해당한다.
-
2개의 register와 1개의 immediate(16bit address or constant)를 사용한다.
- rs: source register
- rt: destination/source register
- constant: (-2^15) ~ (2^15 - 1)
- address: rs의 base address에 더해지는 offset -
load, store, beq, bnq와 같은 명령어들이 있다.

J format
-
Jump / Call (unconditional Branch)연산에 해당한다.
-
j와 같은 명령어들이 있다.

[MIPS Pipeline]
파이프라인을 사용하는 이유
아래 그림과 같이 빨래를 예시로 들어본다.
빨래를 순차적으로 수행하게 하면 한 사람이 "세탁기 돌리기 - 건조기 돌리기 - 옷 개기 - 서랍에 정리하기"를 다 마칠 때까지 다른 사람은 빨래를 하지 못한다.
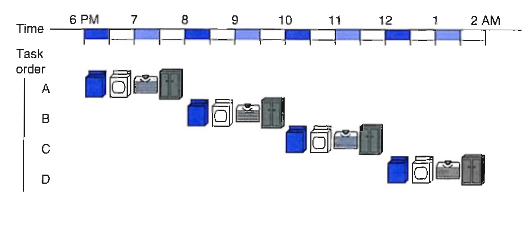
즉, 첫 번째 사람이 6시~6시반에 세탁기 사용을 끝냈기 때문에 세탁기가 비어있음에도 불구하고 두 번째 사람은 8시까지 세탁기를 사용하지 못하게 되는 것이다. 이런 sequential한 방식으로 빨래를 하게 한다면 D는 빨래를 하기 위해 새벽 2시에 잠을 자야한다..ㅠ
첫 번째 사람이 6시 반에 세탁기 사용을 끝내면, 두 번째 사람이 바로 세탁기를 사용하게 하고싶다. D가 좀 더 빨리 잠들 수 있게 해주자. 아래 그림과 같이 빨래를 할 수 있게 한다면 D는 빨래를 끝내기 위해 새벽 2시까지 기다리지 않아도 된다.

이렇게 빨래를 수행하는 방식을 Pipelined 방식이라고 한다. Pipelined 방식을 채택하면 전체 Task가 끝나는 시간을 단축할 수 있어 훨씬 효율적으로 동작할 수 있다는 장점이 있다.
MIPS Pipeline
MIPS instructions는 5 stage로 구성되어있다.
- IF (Instruction Fetch)
- ID (Instruction Decode)
- EX (Execution)
- MEM (Memory Access)
- WB (Write Back)
위에서 말한 Pipelined 방식으로 MIPS instructions를 실행시키면 아래와 같이 돌아간다고 할 수 있다.
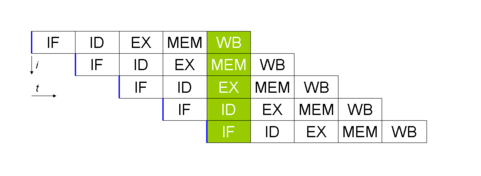
하나의 stage 당 1cycle이 소모된다고 하자. 그렇게 되면 하나의 명령어를 수행하기 위해 총 5cycle이 소모된다.(한 명령어는 5 stage로 구성되기 때문이다.) 이러한 상황에서 5개의 명령어를 실행시킨다고 해보자.
만약 Unpipelined 방식을 채택했다면 한 명령어의 수행이 완전히 끝난 후 다음 명령어가 수행되기 때문에 총 25 cycle이 소모될 것이다.
하지만 Pipelined 방식을 채택한다면 stage 중첩이 가능하기 때문에 위의 그림과 같이 9 cycle이 소모될 것이다. Pipelined 방식이 훨씬 효율적이다.
이와 같이 Pipelined 방식을 사용하면 clock cycle speed를 단축시킬 수 있다. 하지만 이러한 방식에도 한계가 존재한다.
[Hazards]
Pipeline의 한계는 바로 Hazard 가 존재한다는 것이다.
Hazard의 종류로는 Structural Hazard, Data Hazard, Control Hazard가 존재한다.
Structural Hazard
{원인} 하드웨어 리소스 부족 (리소스 충돌)
{예시} Single memory : 메모리는 1개인데 한 cycle에 2개의 instructions가 메모리를 사용(접근)하려고 하는 경우
이러한 경우, 만약 load 명령어가 MEM stage에서 메모리에 접근 중이라면, 다른 명령어들은 메모리에 접근하는 작업을 할 수 없다. 즉, Instruction Fetch 작업이 불가능해진다.
{해결책} 하드웨어 리소스를 늘린다.
Data Hazard
{원인} 명령어를 실행시키기 위해 필요한 데이터가 준비되지 않은 경우
(1) RAW dependency
- Read After Write dependency
- true dependency 라고도 함
(2) WAR dependency
- Write After Read dependency
- anti dependency 라고도 함
- 보통 레지스터가 부족해서, 레지스터를 재사용하는 과정에서 발생할 수 있는 문제점임. 하지만 MIPS 5 stage pipeline에서는 발생하지 않음.
(모든 instructions가 5 stage로 이루어져있으며, read 단계는 항상 stage2에서, write 단계는 항상 stage5에서 수행되기 때문)
(3) WAW dependency
- Write After Write dependency
- output dependency 라고도 함
- WAR과 마찬가지로, MIPS 5 stage pipeline에서는 발생하지 않음.
(모든 instructions가 5 stage로 이루어져있으며, write 단계는 항상 stage5에서 수행되기 때문)
사실상 WAR과 WAW는 register 개수가 모자라기 때문에 reuse하는 과정에서 문제가 발생할 수 있다. 따라서 register의 개수만 늘려준다면 예방이 가능하다.
하지만 RAW는 register의 개수를 늘려준다고 해서 해결할 수 있는 문제가 아니다. RAW dependency 문제를 해결하기 위해서는 Forwarding 이라는 방법을 사용해야 한다.
{Avoid data hazard: Forwarding}
RAW dependency 문제를 피하기 위해 사용되는 방법이다.
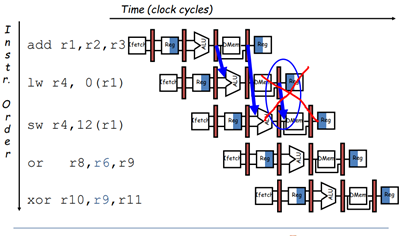
예를 들어, 위 그림에서는 add 연산에서의 r1과 lw 연산에서의 r1 사이에서 RAW dependency 문제가 발생한다.
add 연산에서는 r2 레지스터의 값과 r3 레지스터의 값을 더해서 r1 레지스터에 결과를 저장하는 연산을 수행하고 있다. 이 때 실질적으로 r1에 값이 저장 완료되는 순간은 EX stage 직후이다.
lw 연산에서는 r1 레지스터를 read하고 있다. 이 때 r1 레지스터가 실질적으로 read되는 순간은 ID stage에서 EX stage로 넘어가는 단계이다.
따라서 add 연산의 stage3 이후의 시점에서 lw 연산의 stage2~stage3 사이의 시점으로 r1을 포워딩 해줄 수 있다. 이를 통해 r1의 RAW dependency 문제 해결이 가능하다.
{Forwarding의 한계: Load-Use hazard}
하지만 Forwarding이 항상 RAW dependency 문제를 해결해주는 것은 아니다.
Load 연산의 경우 실질적으로 MEM stage에서 load 작업을 완료하기 때문에, lw 명령어 이후에 add/sub와 같은 명령어가 실행된다면, 여전히 dependency 문제가 남아있을 수 있다.
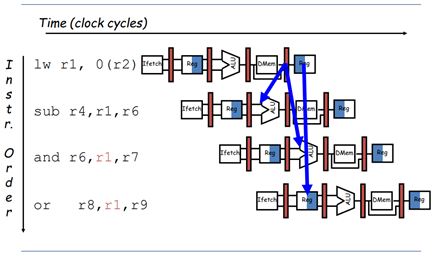
위와 같은 경우가 발생할 수 있다. lw 명령어는 메모리에 접근하여 데이터를 불러오고, 이를 r1 레지스터에 저장하는 작업을 수행한다. lw가 r1 레지스터에 데이터를 저장 완료하는 시점이 바로 MEM stage 직후이다.
그 밑에 sub명령어 역시 r1을 operand로 사용하고 있다. sub는 r1 레지스터의 값에서 r6 레지스터의 값을 뺀 후, 그 결과를 r4 레지스터에 저장하려고 한다. add/sub와 같은 산술 연산은 EX stage에서 이루어지기 때문에, sub가 연산을 하기 위해 r1 레지스터를 사용하려면 적어도 EX stage 전에 r1 레지스터의 값을 가져와야 한다.
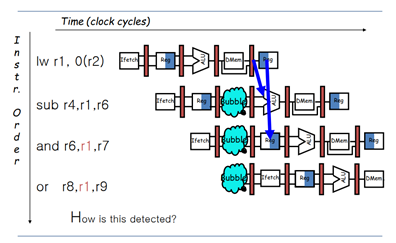
하지만 위 그림에 따르면 lw의 MEM stage보다 sub의 ID-EX stage가 더 앞쪽에 있다. Forwarding은 뒤에서 앞으로 이루어질 수 없기 때문에, 이러한 경우에는 Forwarding으로 dependency를 해결할 수 없다.
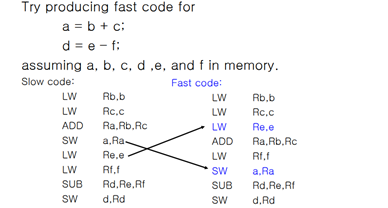
{Avoid Load-Use hazard: Software Scheduling}
다행히도, load hazard 역시 피할 수 있는 방법이 존재한다. 바로 명령어의 실행 순서를 바꾸어주는 것이다. 이러한 스케줄링 방법을 통해 load hazard 역시 어느정도 극복이 가능하다.
Control Hazard
{원인}
Branch/Jump/Call/Return과 같은 명령어들 때문에 실행 순서가 바뀌어서 다음에 수행해야 할 명령어를 판단하기 어려운 경우

{해결}
(1) Stall
branch direction이 명확해질 때까지 stall 한다.
(2) Predict Branch Not Taken
branch가 수행되지 않을 것이라고 미리 예측하는 방식이다.
branch가 수행되지 않을 것이기 때문에, branch 명령어 바로 다음에 등장하는 명령어를 수행하면 된다. 즉, 다음에 수행할 명령어의 위치가 이미 계산되어 있다. (PC+4)
참고로 MIPS에서는 평균적으로 47%의 branches가 not taken된다.
not taken이라고 예측했는데, 실제로는 branch가 taken되는 경우 여전히 control hazard가 발생한다.
(3) Predict Branch Taken
branch가 수행될 것이라고 미리 예측하는 방식이다.
하지만 다음에 수행될 명령어의 target address를 알지 못하기 때문에 여전히 1 cycle 만큼의 페널티가 존재한다.
참고로 MIPS에서는 평균적으로 53%의 branches가 taken된다.
taken이라고 예측했는데, 실재로는 branch가 not taken되는 경우 여전히 control hazard가 발생한다.
(4) Delayed Branch
NOP을 삽입하여 처음부터 Branch hazard가 발생하지 않도록 하는 방법이다.
즉, branch 여부와는 관계 없이 다음 명령어가 실행되는 문제점을 방지하기 위해, branch와 다음 명령어 사이에 NOP을 넣어 문제를 해결하는 것이다.
따라서 1 clock 만큼의 지연이 발생하고, 이후 branch가 정상적으로 수행된다. (넘어가야 할 위치로 넘어간다.)
참고로, 5 stage pipeline에서는 1 slot delay(1 NOP)가 적절하다. MIPS에서는 1 slot delay 방식을 사용한다.
NOP을 사용하면 어쨌든 1 clock 만큼의 딜레이가 발생하기 때문에 낭비가 생긴다. 이러한 낭비를 줄이기 위해 NOP 자리에 다른 useful한 명령어를 채워넣자는 취지에서 나온 것이 delay slot scheduling이다. 즉, branch와 어떤 dependency도 없으면서, branch 여부와 관계없이 반드시 실행되는 명령어들을 NOP자리에 채우는 것이다.
{delay slot scheduling}
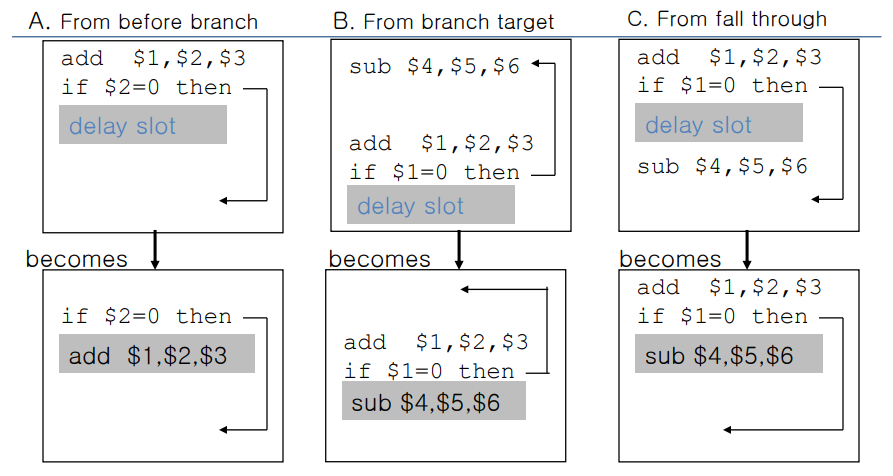
위와 같이 3가지 후보가 있다.
A. branch 전에 independent한 instruction이 있다면, 해당 instruction을 slot에 채워넣는다. (CPI 손실이 없는 제일 이상적인 경우이다.)
B. branch를 통해 점프할 위치에 있는 instruction을 미리 가져다가 채워넣자.
- A에 비해서는 효율성이 좀 떨어진다.
- 점프할 위치에 있는 애를 미리 가져왔으므로, 원래 branch의 target이었던 address의 다음 줄로 다시 타겟팅해주어야 한다.
- 이는 무조건 branch가 taken된다는 가정 하에 이루어지므로, not taken되면 문제가 생길 수 있다.
C. branch의 delay slot 바로 다음 줄에 나오는 instruction을 미리 가져다가 채워넣자.
- 얘도 A에 비해 효율성이 좀 떨어진다.
- 이는 branch가 not taken된다는 가정 하에 이루어진다면 문제가 발생하지 않겠지만, taken되면 문제가 생길 수 있다.
- 따라서 taken된다는 가정까지 고려하여 "실행시켜도 문제 없는 instruction"을 채워주도록 한다.
위와 같이 delay slot을 채워서 control hazard를 해결하려고 했을 때, 결과적으로 delay slot을 60%정도 채울 수 있었다고 한다. 즉, 40%의 경우에서는 delay slot을 채우지 못해서 그냥 NOP으로 채웠다는 것이다.
또한 delay slot이 경우에서도 80% 정도의 instructions만이 useful했다고 한다. (즉, 별로 useful하지 못한 instructions가 채워진 경우가 20%라는 의미이다.)
이를 종합해봤을 때, 대략 50%(60% * 80%)정도 경우에서 delay slot이 useful한 instructions로 채워졌다고 할 수 있다.
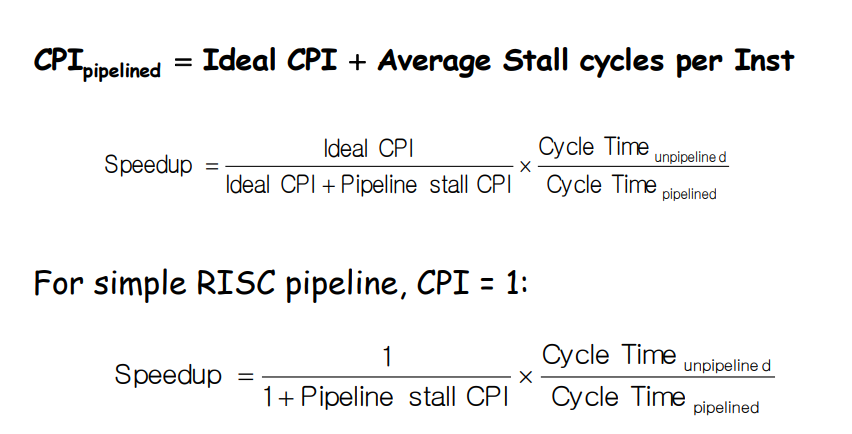
+) Evaluating Branch Alternatives
Pipeline speedup = Pipeline depth / (1 + Branch frequency * Branch penalty)
→ Branch hazard만 고려했을 경우의 speed up (data와 structure hazard는 일단 빼고 계산)
→ MIPS에서는 Pipeline depth가 5
→ 1은 ideal CPI
→ Branch frequency * Branch penalty는 branch 때문에 발생하는 latency (pipeline stall CPI)
→ 결국 분모는 average CPI = ideal CPI + Pipeline Stall CPI
통계적으로 전체 instruction들 중 약 20%정도가 jump나 branch가 포함된 instruction이다. 여기서 4%의 unconditional branch(jump)이고, 6%가 untaken conditional branch(branch)이고, 나머지 10%가 taken conditional branch(branch)이다.
이러한 조건에서 위에서 설명한 Control Hazard 해결방법 4가지를 비교해본다.

(1) Stall pipeline
- 전체적으로 20%의 branch instruction이 발생하므로 branch frequency는 0.2로 계산할 수 있다.
- 따라서 CPI는 1(ideal cpi) + 0.2(branch frequency) * 3(branch penalty) = 1.6이다.
- unpipelined랑 비교했을 때 5 / 1.6 = 약 3.1
- stall pipeline과 비교했을 때 (자기 자신이므로) 1.6 / 1.6 = 1
(2) Predict taken
- predict taken이라고 가정했을 경우: 어쨌든 항상 branch 바로 다음줄에 있는 명령어가 실행되므로 1 stall이 발생한다.
- CPI = 1 + 0.2 * 1 = 1.2
- unpipelined랑 비교했을 때 5 / 1.2 = 약 4.2
- stall pipeline과 비교했을 때 1.6 / 1.2 - 약 1.33
(3) Predict not taken
- predict not taken이라고 가정했을 경우: branch가 실제로 not taken되는 경우에는 stall이 안생긴다. 따라서 branch taken되는 경우에 대해서만 고려하면 된다. (14%)
- CPI = 1+ 0.14 * 1 = 1.14
- unpipelined랑 비교했을 때 5 / 1.14 = 약 4.4
- stall pipeline과 비교했을 때 1.6 / 1.14 - 약 1.4
(4) Delayed branch
- branch가 taken되든 안되든 컴파일러가 delay slot을 채워넣는 방법이다. 위에서 언급된 바로는 delay slot의 50%정도만이 useful하게 채워졌다고 했으므로, 나머지 50%에 대해서는 branch hazard가 남아있다. 따라서 branch penalty를 0.5정도로 고려한다.
- CPI = 1 + 0.2 * 0.5 = 약 1.10
- unpipelined랑 비교했을 때 5 / 1.10 = 약 4.5
- stall pipeline과 비교했을 때 1.6 / 1.10 = 약 1.45
