[AI] Game Search

게임 정의

• 참가자 2명
• 제로섬 게임: 한 명이 승리하면 다른 한 명은 패배 (윈윈하는 결과는 없음)
• 순차적인 게임

여기서는 Tic-Tac-Toe 게임을 예시로 하여 게임 알고리즘에 대해 정리한다.

• 한 참가자를 Max, 다른 참가자를 Min이라고 두고, 게임은 항상 Max가 먼저 시작한다.
• 항상 상대방이 최선의 수를 둔다고 가정한다.
  
  

MiniMax Algorithm

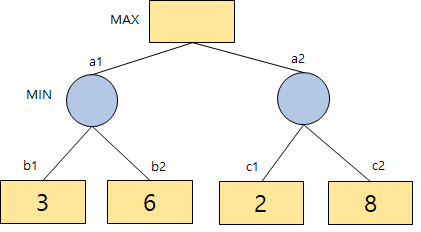
b1, b2, c1, c2는 단말노드이다. 위 그림과 같이 게임 트리가 완성되었다고 하자. 각 노드의 평가 값(휴리스틱 값)이 크면 MAX에게 유리하고, 평가 값이 낮으면 MIN에게 유리해진다.

단말 노드에 대한 평가가 끝나면 밑에서부터 거슬러 올라간다. 이 때 MIN 입장에서는 평가 값이 낮은 노드를 선택하는 것이 좋고, MAX 입장에서는 평가 값이 높은 노드를 선택하는 것이 좋다. 따라서 아래와 같이 선택이 된다.

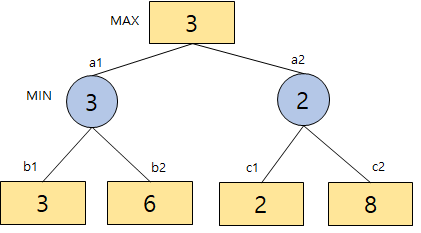
MIN 입장에서는 b1과 b2중 b1의 평가 값이 더 작으므로 3을 선택하고, c1과 c2 중 c1의 평가 값이 더 작으므로 2를 선택한다. 반대로, MAX 입장에서는 a1과 a2 중 a1의 평가 값이 더 크므로 3을 선택한다.

이러한 알고리즘을 MiniMax 알고리즘이라고 한다.

Pseudo Code

function minimax(node, depth, player)
    if depth == 0 or leaf node:
        return 해당 node의 heuristic 값
    if player == 'max':
        value = -(무한대)
        for each child of node:
            value = max(value, minimax(child, depth-1, 'min')
        return value
    else:
        value = +(무한대)
        for each child of node:
            value = min(value, minimax(child, depth-1, 'max')
        return value

현재 노드로부터 가능한 자식 노드들을 생성하고, 각각에 대해 minimax 함수를 재귀적으로 호출하여 자기 자신에 대해 최선의 이동을 선택한다. (max 참가자는 더 큰 값을 선택, min 참가자는 더 작은 값을 선택)

MiniMax 알고리즘은 완벽한 깊이 우선 탐색이 가능하다. 따라서 트리의 최대 depth를 m, 각 노드에서 만들 수 있는 자식 노드 수가 b라고 할 때 시간복잡도는 O(b^m)이다.

Tic-Tac-Toe에 MiniMax Algorithm 적용

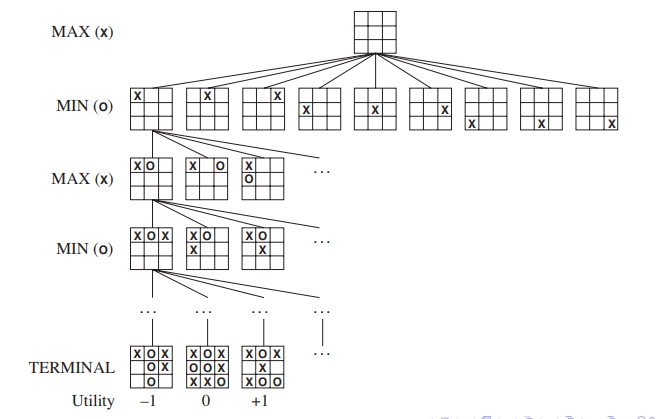
각 노드가 하나의 보드 상태를 나타낸다고 하자.

• 보드의 상태가 MAX 참가자에게 유리할 경우, 해당 노드의 평가 값은 +1이 된다.
• 반대로 MIN 참가자에게 유리할 경우, 해당 노드의 평가 값은 -1이 된다.
• 비길 경우 평가 값은 0이다.

Alpha-Beta Pruning

위에서 살펴본 바와 같이 MiniMax 알고리즘의 시간복잡도는 exponentially increase한다는 점에서 문제가 있다. 이를 보완하기 위해 나온 것이 alpha-beta pruning이다.

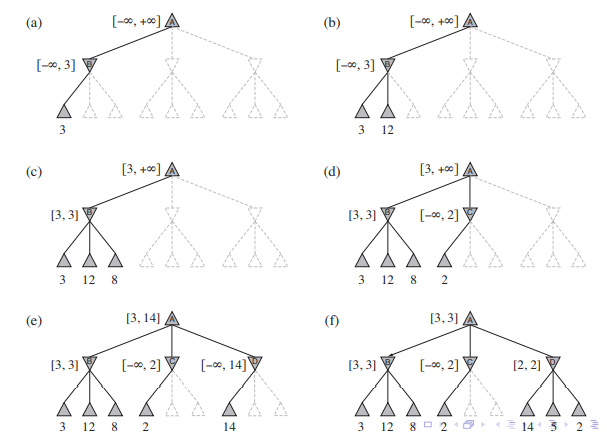
위 그림과 같이 alpha-beta pruning은 minimax algorithm에서 최종 결과에 영향을 미치지 않는 branch를 쳐내는 방식으로 작동한다.

(d) C 노드에서 첫 번째 자식노드만 검사하고 멈추는 이유는, 루트노드인 A는 MAX 값을 얻어야 하므로 현재 max 값으로 들어가있는 3보다 큰 값이 있다면 갱신해주고, 3보다 작은 값이 나온다면 무시해도 된다. C 노드는 MIN 값을 얻어야 하므로 자식노드들 중 가장 작은 값을 얻어야 하므로, 만약 평가 값이 2보다 큰 자식노드가 있더라도 C는 2를 평가 값으로 갖게 된다. A 입장에서는 C가 항상 2 이하의 값을 갖게 되므로 C의 나머지 자식노드는 고려하지 않는 것이다.

Rule

• Alpha 값은 MAX 노드에서만 갱신한다.
• Beta 값은 MIN 노드에서만 갱신한다.
• 만약 Alpha >= Beta이면 가지치기를 한다. (더이상 자식노드를 탐색하지 않는다.)

또 다른 예제는 아래 그림과 같다. (밑에서부터 따라가면서 연습해보기)

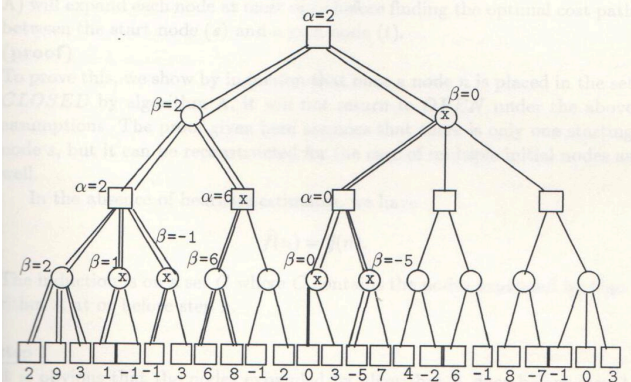
Properties

• Pruning은 최종 결과에 영향을 미치지 않는다.
• Pruning의 효과는 자식 노드 탐색 순서에 영향을 받는다. 예를 들어, 가장 마지막에 탐색하는 자식노드가 Alpha>=Beta 조건을 만족하는 경우에는 결국 모든 자식노드를 탐색하는 것이 된다. 따라서 최악의 경우, MiniMax 알고리즘과 같은 시간복잡도가 나올 수 있다.
• Pruning을 완벽하게 수행하는 경우 시간복잡도는 O(b^(m/2))이다. (모든 노드에 대하여 첫 번째 자식노드에서 Alpha>=Beta가 만족되는 경우이다.)

Pseudo Code

function alphabeta(node, depth, alpha, beta, player)
    if depth == 0 or leaf node:
        return 해당 node의 heuristic 값
    if player == 'max':
        value = -(무한대)
        for each child of node:
            value = max(value, minimax(child, depth-1, 'min')
            alpha = max(alpha, value)
            if alpha >= beta:
                break
        return value
    else:
        value = +(무한대)
        for each child of node:
            value = min(value, minimax(child, depth-1, 'max')
            beta = min(beta, value)
            if alpha >= beta:
                break
        return value