목차
- Cache architecture
- Main memory
- Virtual memory
1. Locality
CPU speed는 굉장히 빠르게 발전하는 반면, memory speed는 더디게 발전하고 있다.이 둘은 현재 차이가 매우 벌어져 있다. 그럼에도 불구하고 컴퓨터가 제대로 돌아가는 이유는 locality 때문이다.
ex) 2차원 배열 index 접근 - row major: source[i][j]가 더 효율적(locality 때문)
1-1. The Principle of Locality
-
Temporal Locality(Locality in Time)
: 이전에 참조된 적이 있는 데이터는 미래에도 계속 쓸 가능성이 높다. -
Spatial Locality(Locality in Space)
: 이전에 참조된 적이 있는 데이터에 대해, 그 주변에 있는 데이터들은 미래에 참조될 가능성이 높다.
1-2. Memory Hierarchy
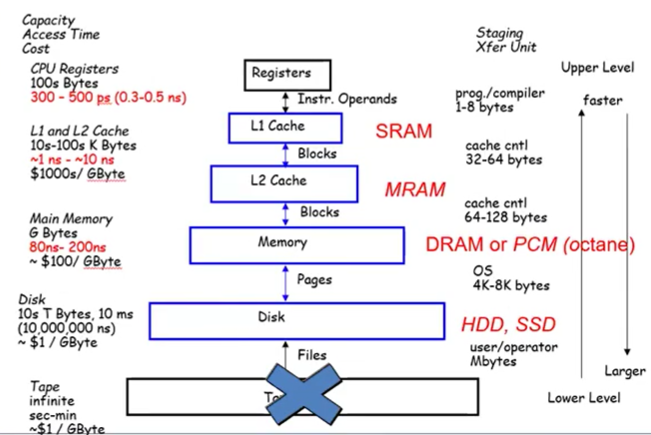
1-3. Locality의 이점
- Memory Hierarchy
- Store everything on disk (모든 data를 disk에 저장하고 가져다 쓸 수 있는 구조)
- 최근에 접근했던 items를 disk에서 DRAM(메인메모리)로 copy할 수 있다
- 더 최근에 접근했던 items를 DRAM에서 SRAM으로 copy할 수 있다
2. Cache
2-1. Direct Mapped Cache
- address에 의해 캐시로 매핑
- only one choice: (Block address) mod (# Blocks in cache)
- Cache의 Field: Tags, Valid Bit, Data
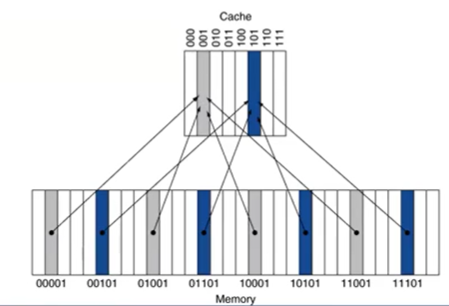
위 그림에서 메모리의 00001주소에 있던 내용이 Cache의 001에 매핑되었다. 즉, 위의 경우 메모리의 마지막 3bit을 이용해 cache의 각 블록에 매핑되어있다. 이 때 cache에 매핑된 각 값들이 memory의 어느 주소에서 온 것인지를 파악하기 위해 tag 속성을 이용한다. 위의 경우 Tag는 메모리 주소에서 앞의 2bit에 해당한다. 따라서 메모리 00001에 저장된 정보는 cache의 001에 저장되고, tag는 00이다.
+) cache의 access단위 = cache block = cache line
(1) Cache 예시
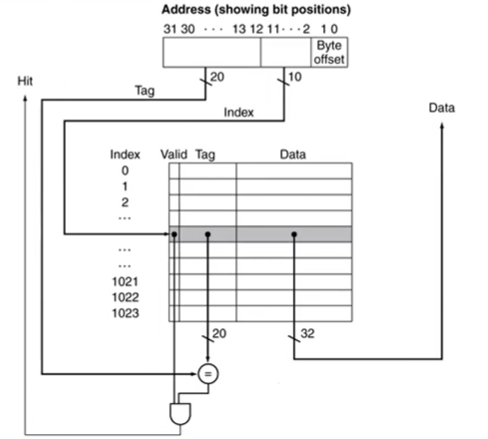
- address: tag bits + index bits + page offset
- cache: valid bit + tag bits + data bits
(2) Block Size
- block size는 클 수도 작을 수도 있다.
- block size가 클수록 cache miss rate이 감소한다. (spatial locality 때문)
- cache의 총 사이즈가 고정되어있는 경우, block size가 크면 그만큼 block의 개수는 감소한다. 이 경우 miss rate이 증가한다.
(3) Cache miss의 종류
-
capacity miss: cache size가 너무 작아서 working set을 감당할 수 없을 때 발생하는 miss
--> 해결책: cache size를 크게 만들어준다. -
conflict miss: bad indexing으로 인한 conflict (hashing conflict)
--> 해결책: set associativity를 늘린다. -
compulsory miss: 맨 처음에(컴퓨터를 막 부팅했을 때) cache에 아무것도 없는데, 이렇게 필연적으로 발생하는 miss (cold miss)
--> 해결책: pre-fetching (앞으로 많이 사용할 것 같은 데이터들을 미리 캐시메모리에 적재한다.)
[Cache miss가 발생한 경우]
- pipeline이 stall 된다.
- hierarchy에 있는 다음 level로부터 block을 fetch해온다. (캐시에 없으면 메인메모리에 접근하여 데이터를 가져온다.)
- 이 때, 다음 level에 있는 데이터 정보를 cache로 가져오고(Data Cache miss), 해당 data를 필요로했던 instruction을 다시 fetch하여 restart해준다(Instruction cache miss).
(4) Write Policy에 따른 cache의 분류
I. Write-Through
- Cache에 write할 때, 그 밑에 있는 hierarchy(메인 메모리)에도 write을 하는 경우
- 하지만 시간이 오래 걸린다는 단점이 있다.
- 이에 대한 해결책 : write buffer
--> cache에서 main memory로 block을 write할 때, 아래 level memory는 매우 바빠진다.
그 다음에 main memory를 read할 상황이 생기면, main memory는 write하느라 현재 바쁜 상태이기 때문에, read를 못하게 된다. 이를 방지하기 위해 cache에서 메모리로 내용을 write할 때, 그 내용을 임시로 저장하는데, 이 버퍼 공간을 write buffer라고 한다.
II. Wrtie-Back
- Cache에 write할 때, 그 밑에 있는 hierarchy에는 write하지 않는 경우
- write-back cache가 memory에 write하는 경우 : 캐시가 꽉 찬 상태인데, 새로운 block이 들어와야 하는 경우. 기존에 있던 block중 하나를 빼서 replace해주어야 한다. 이 때, 앞으로 잘 사용되지 않을 것 같은 dirty block들을 replace하게 되는데, 이 dirty block들에 있는 내용들은 앞으로 사용될 가능성이 적으므로, 메인 메모리에 빨리 써줄 필요가 없다. 그래서 일단은 write buffer에 임시로 저장해놓고 천천히 메모리로 옮겨주는 방식으로 작업하기도 한다.
즉, 원래 순서는, 캐시 메모리에 있는 dirty block을 새로이 필요한 내용으로 replace해주는 경우, dirty block 내용을 메모리에 쓰고 -> 메모리에서 필요한 내용 읽어서 -> 캐시메모리로 적재시키는게 원래 순서임. 근데 이 때 dirty block 내용을 메모리에 쓰는 작업을 함으로써 시간이 오래 걸릴 수 있으므로, dirty block 내용은 write buffer에 넣어두고(이건 시간이 1cycle밖에 안걸림), 메모리에서 필요한 내용 읽기 -> 캐시메모리로 적재 -> 나중에 시간 남으면 write buffer의 내용을 메모리에 쓰기 순서로 진행한다.
2-2. Associative Cache
(1) Fully associative
- 주어진 block이 아무 cache entry에 매핑될 수 있다.
- 모든 entry들이 한꺼번에 search되어야 한다.
- comparator per entry가 expensive하다.
(2) n-way set associative
- 각 set에는 n개의 entry들이 존재한다.
- block number를 통해 어떤 set으로 매핑될지 결정된다.
-> (Block number) % (# of sets in cache) - 한꺼번에 모든 entry들을 search
- n comparators (less expensive)
2-3. Cache 비교

(1) Direct mapped
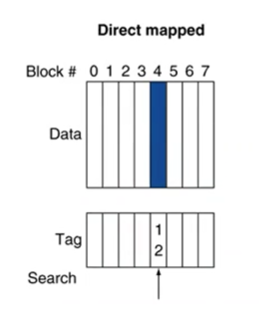
: block address가 12이고, block size가 8일 때, 12 mod 8 = 4이므로, cache의 4번 인덱스에 데이터가 저장되고, tag에는 원래 주소인 12가 저장된다.
(2) Set associative (2-way)
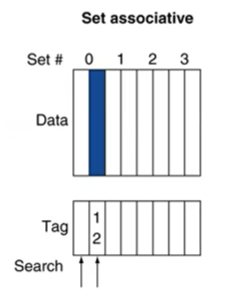
: block address가 12이고, set size가 4일 때, 12 mod 4 = 0이므로, cache의 0번 인덱스 set 중 하나에 데이터가 저장된다.
(3) Fully associative
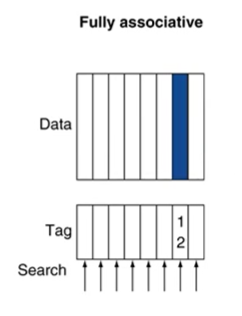
: cache의 어느 인덱스에든 데이터가 매핑될 수 있다. (conflict miss가 거의 발생하지 않음)
3. Main memory
메인메모리에서 캐시로 데이터 가져올 때
- 접근해야할 메모리의 address transfer 하는데 1bus cycle 소모
- DRAM으로 실제 접근&필요한 데이터 찾아내는데 15 bus cycle이 소모
- 찾아낸 데이터를 캐시로 transfer하는데 1 bus cycle이 소모
3-1. 1-word-wide memory인 경우
만약 캐시의 4-word block으로 가져올 때. DRAM은 1-word-wide DRAM (1word 단위로 access가능한 상황)
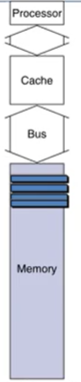
- address transfer: 1bus
- DRAM access: 4 * 15 bus = 60
- data transfer: 4 * 1bus = 4bus
- 총 miss penalty = 1 + 60 + 4 = 65 bus cycles
- bandwidth = 16bytes(=4word) / 65 cycles = 0.25B/cycle (1word = 4bytes)
3-2. 4-word-wide memory인 경우
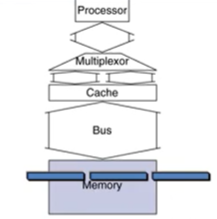
- address transfer: 1bus
- DRAM access = 15bus
- data transfer = 1 bus
총 miss penalty: 17bus cycles
bandwidth = 16bytes/17 cycles = 0.94B/cycle
3-3. 4-bank interleaved memory
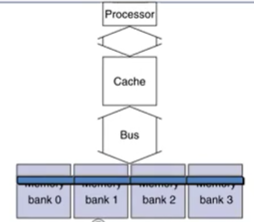
전달된 address를 기반으로 parallel하게 DRAM access가능
하지만 data transfer는 순차적으로 수행. (bus는 1개..)
- address transfer: 1 bus
- DRAM access: 15 bus
- data transfer = 1 * 4 bus
총 miss penalty: 20 bus cycles
bandwidth = 16 / 20 = 0.8B/cycle
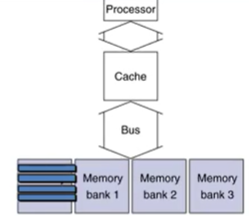
worst case: bottleneck 발생한 경우.
위 그림과 같이 찾으려는 모든 word block이 하나의 bank에 몰려있는 경우, 1-word-wide memory와 다를게 없어진다.
이러한 경우를 최대한으로 줄이는 방법: bank의 수를 늘린다.
4. Cache Performance 계산

4-1. CPI 예제
문제)
- I-cache miss rate = 2%
- D-cache miss rate = 4%
- Miss penalty = 100 cycles
- Base CPI(ideal cache) = 2
- Load & Stores are 36% of instructions
해결)
- Miss cycles per instruction
-> I-cache: 0.02 x 100 = 2
-> D-cache: 0.04 x 100 x 0.36 = 1.44 - Actural CPI = I-cache + D-cache + Base CPI = 2 + 1.44 + 2 = 5.44
따라서 Ideal CPU는 5.44/2 = 2.72배만큼 더 빠르다.
4-2. AMAT 예제
AMAT
= Average Memory Access Time
= Hit time + Miss rate * Miss penalty
문제)
- CPU with 1ns clock
- hit time = 1 cycle
- miss penalty = 20 cycles
- I-cache miss rate = 5%
해결)
- AMAT = 1cycle + 20cycles * 0.05 = 2ns
따라서 2 cycles per instruction
5. Replacement Policy
-
Direct mapped
: no choice (그냥 정해진 entry에 무조건 넣어야 함) -
associative (n-way set associative / fully-associative)
: non-valid entry에 우선 넣는다. 만약 non-valid entry가 없다면, valid한 애들 중에 하나 고른다.
5-1. LRU (Least-Recently Used)
: 가장 오랫동안 unused된 애를 고른다. (Temporal Locality를 사용)
LRU 예제
| way0 | way1 | way2 | way3 |
|---|---|---|---|
| 0(latest) | 3(oldest) | 1 | 2 |
숫자가 작을수록 가장 최근에 access된 entry이다.
첫 번째 row의 경우, way0이 가장 최근, way1이 가장 오래 전에 access되었다. (least recently used)
따라서 LRU에 따르면, 첫 번째 row에서 replace할 때 way1이 선택되어야 한다.
참고로, 위 예제에서는 4 way이므로 access에 대한 값을 2bit으로 나타낼 수 있다.
| 00 -> 01 | 11 -> (1)00 | 01 -> 10 | 10 -> 11 |
|---|
따라서 다음 clock에서는 way1의 값이 0이 된다. 결국 값이 0인 곳이 least recently used인 셈이다. (replace는 update된 것을 갖고 해야함)
5-2. Random
6. Multilevel-Caches
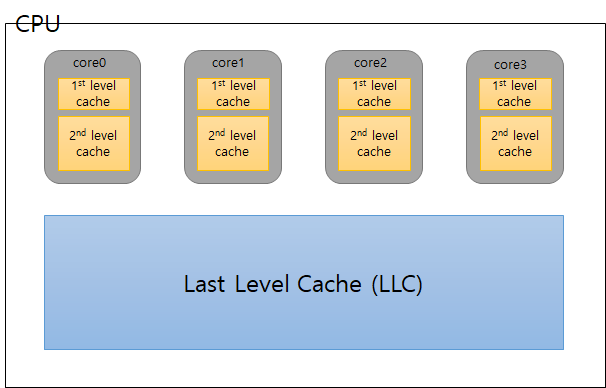
1st level cache(Primary Cache)
: 이 경우, 캐시의 사이즈를 너무 크게 할 수 없다. - 코어가 매 사이클마다 액세스 해야하고, 속도가 매우 빨라야하기 때문에 너무 사이즈가 크면 안된다. 그러다보니 miss rate이 늘어나는 현상이 발생한다. 이 때, 만약 2nd cache나 last cache(3rd cache)가 없다면, 1st cache에서 miss가 발생했을 때, 바로 메인 메모리로 액세스 해야하는데, 이는 penalty가 매우 크다. 이를 방지하기 위해 2nd level cache를 만든다.
-> focus on minimal hit time
2nd level cache(L2 cache)
-> focus on low miss rate to avoid main memory access
-> hit time has less overall impact
1st level cache : fast & small 하게 만들어야 함
2nd level cache : 1st보다는 slower & larger but 여전히 faster thatn main memory
+) 2 level cache일 때의 L1 캐시 사이즈 < single level cache 사이즈
+) L1 캐시의 block size < L2 캐시의 block size
6-1. Multi level cache의 장점 - 예제
조건
- CPU base CPI = 1
- clock rate = 4GHz
- miss rate/instruction = 2%
- main memory access time = 100ns
+) miss penalty: 몇 cycle이 지나야 miss된 block을 갖고올 수 있는가
+) miss penalty = main memory access time / clock cycle
+) Effective CPI = base CPI + miss rate * miss penalty
single level cache(Primary cache)인 경우
- miss penalty = 100ns/0.25ns = 400cycles
- Effective CPI = 1 + 0.02 * 400 = 9
2 level cache(L2 cache)를 붙인 경우
- access time = 5ns (L1캐시에서 L2캐시로의 access time)
- global miss rate to main memory = 0.5% (L1도 miss, L2도 miss일 경우)
2가지 케이스를 고려한다.
1) Primary miss & L2 hit (L1에서의 miss)
- miss penalty = 5ns / 0.25ns = 20cycles
2) Primary miss & L2 miss (L1도 L2도 miss)
- miss penalty = 400cycles
따라서 CPI = 1 + 0.02 x 20 + 0.005 x 400 = 3.4
single level VS. 2 level
2 level의 CPI가 3.4이고, single level의 CPI가 9이므로
L2 cache를 붙였을 때가 9/3.4 = 2.6만큼 더 성능이 좋다.
7. Virtual Memory
7-1. Virtual Address VS. Physical Address
physical address: 물리적으로 존재하는 메모리 공간에 주소 체계를 부여한 것
예를 들어, PC의 내장 메모리로 16기가 DRAM이 있고, 외부에서 연결한 I/O device의 메모리 용량이 1GB라고 할 때, 이 공간들에 접근하기 위해서는 주소가 필요하다. 이를 위해 DRAM에는 0~16기가에 해당하는 주소들을 부여할 수 있고, I/O device에는 16~17기가에 해당하는 주소들을 부여할 수 있다. 이 때 부여된 주소들을 physical address라고 한다.
virtual address: 사용자/응용 프로그램이 사용하는 메모리 주소
프로그램마다 독자적으로 갖고 있다.
프로그램을 구동하면 process가 동작하고, 이 때 각 process에는 별도의 메모리 공간이 부여된다. 이 때 부여되는 공간을 virtual address space라고 한다.
virtual memory: 결국 실제 메모리 공간을 사용하기 위해서는 virtual address를 physical address로 매핑해주어야 한다. 이러한 scheme 자체를 virtual memory라고 한다. (virtual address를 physical address로 매핑해주는 행위)

프로그램을 실행할 때, 코드의 모든 부분이 항상 필요한 것은 아니다. (If문과 같이 예외처리를 수행하는 코드는 아예 실행되지 않을 수도 있다.) 따라서 전체 코드를 항상 물리적 메모리 공간에 적재하는 것은 비효율적이다. (실제로는 필요없는 코드 때문에 메모리 용량을 많이 차지할 수도 있다.) 따라서 각 프로그램은 우선 본인에게 주어진 가상의 메모리 공간에 코드를 올려둔 뒤, 각 메모리 공간에 가상 주소를 할당한다. 이후 실제로 프로그램이 run하는데 필요한 코드들을 물리적인 메모리 주소로 매핑하여 사용하게 된다.
7-2. Virtual Memory
- 메인 메모리를 캐시처럼 사용
- 여러 프로그램들이 메인 메모리를 공유
- CPU와 OS는 virtual address를 physical address로 변환해줌 (virtual memory의 block(page-한 번에 이동하는 데이터 단위)들을 physical memory의 block으로 매핑)
캐시 | virtual memory
block = page
miss = page fault
7-3. Address Translation
virtual address와 physical address의 매핑을 알아야 하는 이유
: virtual memory에서 miss나면 -> 캐시에서 가져옴 -> 캐시에서도 miss나면 -> main memory(physical address)로 접근 (필요한 데이터가 물리 메모리의 어디에 있는지 알아야 갖고 올 수 있기 때문)
이 때, translation을 위해 virtual memory와 physical memory 사이에 존재하는 매핑 테이블을 page table이라고 한다.
virtual address의 구성: virtual page number & page offset
physical address의 구성: physical page number & page offset
page table: virtual page number를 input으로 받아서 physical page number를 뱉어냄(output) -> virtual page number가 page table의 index임
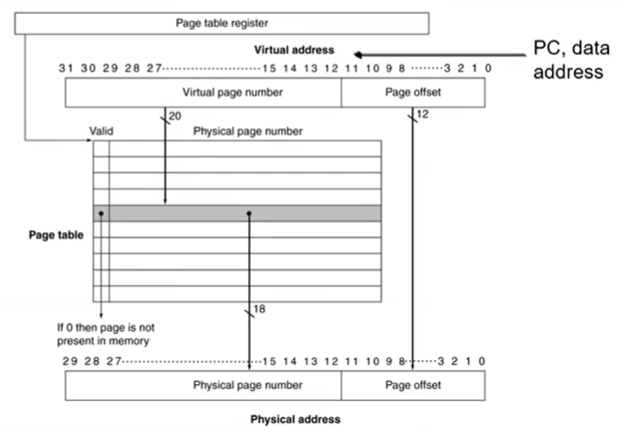
- virtual address space = 2^32 = 4GB
- page offset size = 2^12 = 4KB
- physical address space = 2^30 = 1GB
PTE = page table entry
7-4. Page Fault
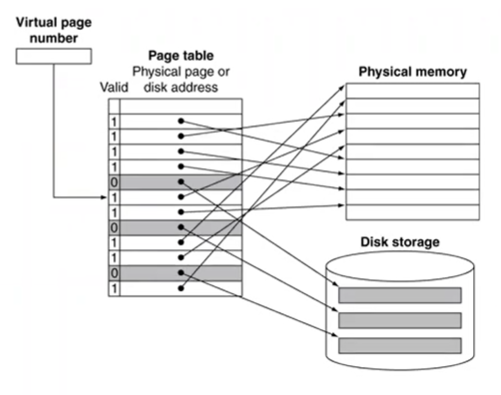
찾으려는 page가 main memory에 없는 경우, disk에서 해당 데이터가 담긴 page를 갖고 들어와야 한다.
page fault rate을 줄이기 위한 알고리즘으로 LRU replacement가 있는데,
- PTE set에 reference bit을 두고, 해당 page로 access한 경우 1로 세팅해준다.
- 일정 시간이 지나면 OS에 의해 reference bit이 0으로 초기화된다.
- reference bit이 0인 경우, 최근에 접근한 page가 아니라고 판단할 수 있다.
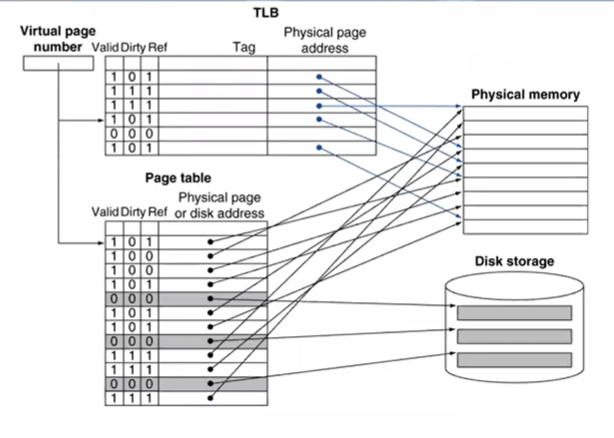
- reference bit: 해당 page로 access(read / write)한 경우 1로 set
- dirty bit: 해당 page가 update(write)된 경우 1로 set
dirty bit이 1로 세팅된 page의 경우, 나중에 해당 entry가 다른 page로 replaced될 때, 기존 page의 update된 내용을 원래 저장 위치(매핑된 physical address)에 다시 써주어야 한다. (업데이트 여부를 체크해주는 flag bit임)
+) 참고로 TLB, Physical memory, disk storage는 hw이고, page table은 자료구조
page table의 문제점
만약 page table에 원하는 데이터가 없는 경우, main memory로 2번 접근하는 overhead 발생
1. 원하는 데이터가 위치한 주소를 main memory에서 가져와서 PTE에 저장 (virtual address와 매핑)
2. 원하는 데이터 자체를 가져오기 위해 main memory로 접근
이러한 speed 문제를 해결하기 위해 PTE에 대한 cache를 둠 : TLB
7-5. TLB
TLB: Translation Look-aside Buffer
page table에서 많이 사용하는 entry를 캐싱을 해서 갖고 있는 fully associative한 structure이다.
TLB miss
: TLB에 원하는 데이터가 없는 경우
- page가 in memory인 경우 (메인 메모리에 존재하는 경우)
- TLB에 없고, page table에만 있는 경우
: page table에 있는 page를 TLB로 가져와서 업데이트한 후 retry - TLB에 없고, page table에도 없는데, 메인 메모리에는 있는 경우
: memory로부터 원하는 데이터를 PTE로 load, TLB를 업데이트한 후 retry한다.
- page가 not in memory인 경우 (page fault)
- TLB에 없고, page table에도 없고, main memory에도 없는데 secondary storage에 있는 경우
: disk에서 해당 페이지를 physical memory로 적재(이 때 만약 memory에 공간이 없을 경우, victim page를 찾아내서 밀어내고 그 자리에 해당 page를 넣어야 함) -> 그 정보를 다시 page table에 저장 -> 이걸 다시 TLB로 갖고 올라가서 저장
7-6. TLB & Cache Interaction
Memory Access 순서
1. TLB 접근
2. TLB에 저장되어 있는 physical address를 가지고 cache로 access
Access 속도를 빠르게 하는 방법
1) Set-associativity를 늘린다.
2) Page-size를 늘린다.
