Chapter 5. Logistic Regression

2J_Hun·2024년 8월 29일

LogisticRegrssion ML 데이터분석 로지스틱 회귀 머신러닝 사이킷런 파이썬

머신러닝

목록 보기

7/8

Logistic Regression

앞서 우리는 Linear Regression(선형회귀)에 대한 논의를 마쳤습니다.

만일 우리가 분류 문제를 해결해야한다면, GLM의 링크 함수에서 힌트를 얻을 수 있습니다.

우선 이진 분류 문제에 대해 생각한다면, 링크 함수로써 계단 함수를 생각할 것입니다.

1. Unit-Step Function

Unit-Step Function(단위계단함수)는 아래와 같습니다.

f(x) = \begin{cases} 0, & \text{if } x < 0; \\ 0.5, & \text{if } x = 0; \\ 1, & \text{if } x > 0, \end{cases}

1. 예시

from scipy import stats as st
import numpy as np
from matplotlib import pyplot as plt

X_range=list(np.linspace(-4,4,50))
X_range.append(0)
X_range.sort()

def func(x):
  if x<0:
      return 0
  elif x==0:
      return 0.5
  else:
      return 1
  
y_range=np.array([func(x) for x in X_range])

plt.scatter(X_range,y_range)
plt.grid()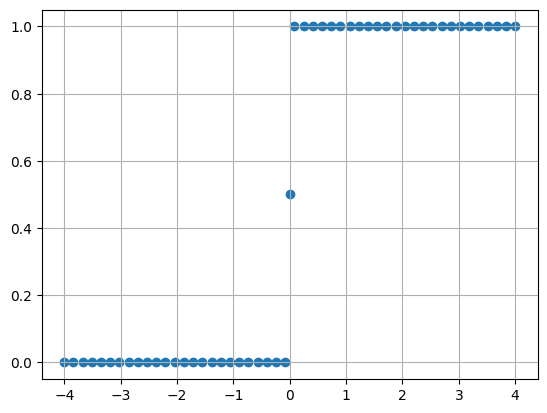

문제는 이전에 언급했듯, 링크함수는 단조 미분가능 함수여야합니다.
위의 계단함수는 미분가능함수가 아닙니다. 따라서 대체 함수를 사용해야합니다.

2. Sigmoid Function

위의 계단함수의 대체 함수입니다.

f(x)=\frac{1}{1+e^{-x}}

이 함수는 Sigmoid(시그모이드) 함수이며 단조 미분가능하므로 링크함수로써 적절합니다.

링크함수로 시그모이드 함수를 사용하다고 가정한다면, 우리의 선형모델은 다음과 같습니다.

y=\frac{1}{1+e^{-(w^Tx+b)}}

이 식을 계속 정리하겠습니다.

e^{-(w^Tx+b)}=\frac{1}{y}-1

w^Tx+b=-ln(\frac{1-y}{y})=ln(\frac{y}{1-y})

여기서 $y$ 를 샘플 $x$ 가 양성(의 라벨)일 가능성으로 본다면, $1-y$ 는 음성의 가능성입니다.

여기서 $\frac{y}{1-y}$ 를 Odds(오즈), $ln(\frac{y}{1-y})$ 를 Log Odds(로그 오즈)라고 합니다.

특히, $ln(\frac{y}{1-y})$ 를 logit(로짓이라고도 부릅니다.

이를 미루어보면 로지스틱 회귀 이름의 의미를 유추해볼 수 있습니다.

2. 예시

from scipy import stats as st
import numpy as np
from matplotlib import pyplot as plt

X_range=list(np.linspace(-8,8,500))
X_range.append(0)
X_range.sort()

def sigmoid(x):
  return 1/(1+np.exp(-x))
  
y_range=np.array([sigmoid(x) for x in X_range])

plt.plot(X_range,y_range)
plt.grid()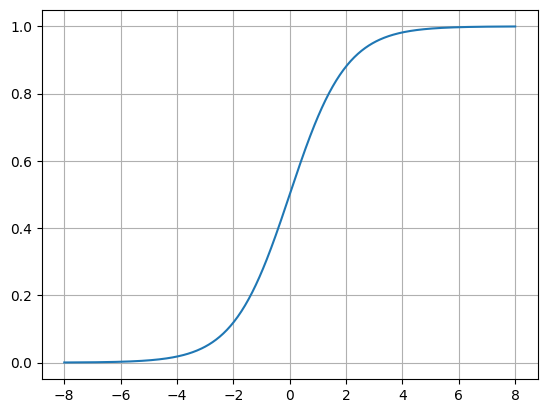

3. Optimization

위의 설명을 통해 우리는 아래와 같은 식을 만들 수 있습니다.

p(y=0 | x)=\frac{1}{1+e^{w^Tx+b}}

p(y=1|x)=\frac{e^{w^Tx+b}}{1+e^{w^Tx+b}}

이를 기반으로 우리는 $w^*,b^*$ 을 찾아야합니다.
이때 maximum likehood method(최대우도법)을 이용합니다.
(데이터 세트 $\{(x_i,y_i)\}_{i=1}^{m}$ 을 가정하겠습니다.)

\ell(w,b)=\sum_{i=1}^{m} \ln p(y_i|x_i;w,b)

각 샘플이 실제 레이블에 속할 확률이 높으면 높은 성능을 기대한다는 의미로도 해석됩니다.

식을 간단화하기 위해 아래와 같은 치환을 해보겠습니다.

w'=(w,b) \\ x_i'=(x_i,1)

이를 통해 우리는 다음과 같은 식을 얻습니다.

w^Tx_i+b=(w')^Tx_i'\\ \ln p(y_i)=y_ip_1(x_i';w')+(1-y_i)(1-p_1(x_i';w'))

3.1 위의 확률식에 대한 추가설명

각 샘플은 독립적이고, 이진 라벨값(1 혹은 0, 양성 혹은 음성 등)을 가지므로 베르누이 확률분포를 따릅니다.
따라서 아래의 베르누이 확률분포에 의해

p(y|x)=p(y=1|x)^yp(y=0)^{1-y}

로 나타낼 수 있습니다.
이해를 돕기 위해 $y_1=1$ 이라고 가정해보죠.

p(y_1)=p(y=1|x';w')^{1}p(y=0|x';w')^{1-1}=p(y=1|x';w')

만약 $y_2=0$ 이라면 아래와 같습니다.

p(y_2)=p(y=1|x';w')^{1-1}p(y=0|x';w')^{1-0}=p(y=0|x';w')

따라서 로그 우도는 아래와 같습니다.

\ln p(y|x)=y\ln p_1(x)+(1-y)\ln p_0(x)

(여기서 $p_i(x)=p(y=i|x)$ 입니다)

따라서 아래와 같이 정리가 가능합니다.

\ell(w') = \sum_{i=1}^{n} \left[ y_i ({w'}^T x_i') - \ln (1 + e^{{w'}^T x_i'}) \right]

이 값을 최대화 한다는 것은 $-\ell(w')$ 을 최소화하는 것과 같습니다.

최적값을 구하는 방법은 경사하강법, 뉴턴법 등 다양합니다.
기본적으로 $\ell(w')$ 은 아래와 같이 고차 미분가능 컨벡스(convex) 함수입니다.

\frac{\partial}{\partial w'}\ell=-\sum_{i=1}^{m}[x_i'(y'-\frac{e^{w'^Tx_i'}}{1+e^{w'^Tx_i'}})]=-\sum_{i=1}^{m}[x_i'(y'-p_1(x_i';w'))]

3.2 예시(직접구현)

유명한 데이터셋인 아이리스 데이터 셋으로 설명하겠습니다.

from sklearn import datasets as skdata
from pandas import DataFrame
import numpy as np

data=skdata.load_iris(as_frame=True,return_X_y=True)
X=DataFrame(data[0])
y=DataFrame(data[1])
name_map=dict(zip([0,1,2],['setosa', 'versicolor', 'virginica']))

y.target=y.target.map(lambda x:name_map[x])

이처럼 데이터 세트를 준비합니다.

우선 이진분류 모델을 만들기 위해, 그리고 샘플의 개수가 동일하면 좋은 성능을 기대할 수 있으므로, 다음과 같이 라벨값을 채택하겠습니다.

y=y[(y=="setosa")|(y=="versicolor")]
named_y=y.copy()

y.dropna(inplace=True)
X=X.loc[y.index]

y=y.map(lambda x: 1 if x=="setosa" else 0)

"setosa" 와 "versicolor" 두 개의 라벨을 채택한 데이터세트입니다.(각각 50개의 데이터를 가지고 있습니다.)

설명에서 등장했던 시그모이드 함수와 손실함수, 그래디언트(손실함수의 편미분)을 만들겠습니다.

#시그모이드 함수
def sigmoid(x:int):
  return 1/(1+np.exp(-x))

sigmoid_=np.vectorize(sigmoid)

#손실함수의 편미분
def partial_loss(w:np.array,X:np.array,y:np.array):
  p_1=sigmoid_(X@w)
  return -X.T@(y-p_1),p_1

#손실함수(음수를 취하기 전 형태)
def log_loss(p_1:np.array,y:np.array):
  return (y.T@p_1)+(1-y).T@(1-p_1)

#x'만들기
constant=np.ones(shape=(X.shape[0],1))
X_addconstant=np.append(X.values,constant,axis=1)

#초기 w' 세팅(랜덤값)
np.random.seed(1)
w_0=np.random.randn(X_addconstant.shape[1])
w_0=w_0.reshape(5,-1)

이로써 경사하강법을 사용하기 위한 준비는 모두 끝났습니다.
경사하강법을 이용해 최적해를 구해보죠.

mu=0.01 #학습률
epochs=1000 #에포크(학습 횟수)

w_history=[w_0]
loss_history=[]
for i in range(epochs):
  w=w_history[-1]

  p_l,p_1=partial_loss(w,X_addconstant,y.values)
  loss=log_loss(p_1,y.values)

  new_w=w-mu*p_l

  w_history.append(new_w)
  loss_history.append(loss)

마지막 w가 가장 낮은 손실을 가진 해입니다.
물론 위에서는 손실함수에 음수를 채택하지 않아서 높을수록 좋은 성능을 나타냅니다(최대우도법)

우리가 구현한 LogisticRegression모델은 다음과 같습니다.

#최종 모델을 이용한 학습데이터의 p1 값  
final_proba=sigmoid_(X_addconstant@w_history[-1])

여기서 실제 라벨로 예측하기 위해서 hold값을 정해야합니다.
일반적인 값인 0.5로 채택하겠습니다.

hold_func=np.vectorize(lambda x: 1 if x>=0.5 else 0)

훈련이 잘 이루어졌는지 혼동행렬로 확인해봅시다.

pred_y=hold_func(final_proba)
from sklearn import metrics as met

met.confusion_matrix(y_pred=pred_y,y_true=y.values)

손실(성능)값의 변화를 살펴보면 다음과 같습니다.

3.3 예시(사이킷런)

사이킷런은 기본적으로 라벨을 그대로 전달해야합니다.
named_y로 미리 준비해놨으니 그대로 사용하죠.

from sklearn import linear_model as lin

logit_rg=lin.LogisticRegression(penalty=None,max_iter=1000)
logit_rg.fit(X=X.values,y=named_y.values.ravel())

사이킷런은 기본적으로 $l2$ 규제를 사용합니다.(과적합 방지)

우리가 원하는 $w'$ 은 다음과 같이 확인할 수 있습니다.

print("w :",logit_rg.coef_)
print("b :",logit_rg.intercept_,"\n\n")

print("w` :",np.append(logit_rg.coef_,logit_rg.intercept_))

2J_Hun

Good Day! Nice Day!

이전 포스트

Chapter 4. Linear Model

다음 포스트