Chapter 6. Linear Discriminant Analysis

Linear Discriminant Analysis

Linear Discirminant Analysis(선형판별분석) 은 줄여서 LDA로 불리며 전통적인 선형 학습법입니다.

아이디어는 굉장히 단순한데, 샘플을 하나의 직선 위로 투영시키는 것입니다.

같은 클래스에 포함된 샘플들은 가깝게, 서로 다른 클래스에 포함된 샘픓들은 멀게 투영시키는 목적으로 직선을 탐색합니다.

---

1. 시각화를 이용해 이해하기

이전에 사용했던 아이리스 데이터세트를 그대로 활용해봅시다.

from sklearn import datasets as skdata
from pandas import DataFrame
import numpy as np

data=skdata.load_iris(as_frame=True,return_X_y=True)
X=DataFrame(data[0])
y=DataFrame(data[1])
name_map=dict(zip([0,1,2],['setosa', 'versicolor', 'virginica']))

y.target=y.target.map(lambda x:name_map[x])

#이진분류를 위해 라벨값 제한
y=y[(y=="setosa")|(y=="versicolor")]
named_y=y.copy()

y.dropna(inplace=True)
X=X.loc[y.index]

y=y.map(lambda x: 1 if x=="setosa" else 0)

여기서 특성 'sepal length (cm)', 'sepal width (cm) 두가지만 사용해서 시각화를 해보겠습니다.

from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from seaborn import scatterplot

example_X=X.loc[:,X.columns[:2]]
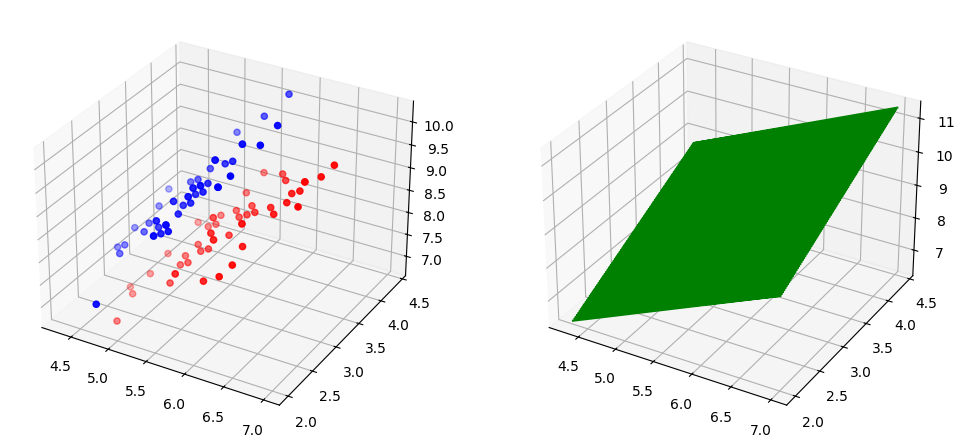
example_y=example_X.values@np.array([1,1]).T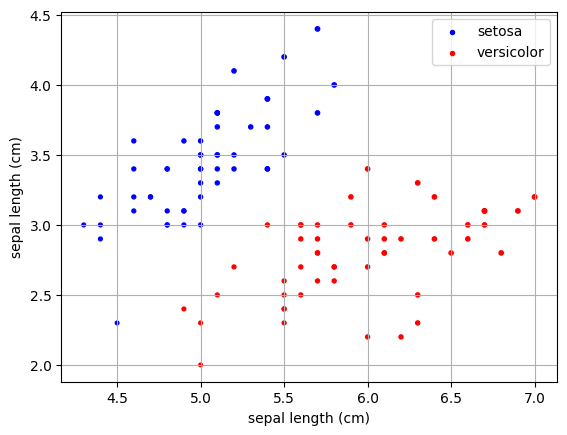

위와 같이 데이터 분포를 띄고 있습니다.
이를 임의의 평면 $y=x_1+x_2=(1,1) \cdot x$ 을 이용헤 시각화한다면 다음과 같은 형태를 보여줍니다.(코드가 복잡하므로 참고만 하시면 됩니다.)

setosa_idx=y[y.values==1].index
versicolor_idx=y[y.values!=1].index

f=plt.figure(figsize=(12,6))
ax1=f.add_subplot(121,projection="3d")
ax1.scatter(example_X.loc[setosa_idx,"sepal length (cm)"]
           ,example_X.loc[setosa_idx,"sepal width (cm)"]
           ,example_y[setosa_idx],label="setosa",color="blue")
ax1.scatter(example_X.loc[versicolor_idx,"sepal length (cm)"]
           ,example_X.loc[versicolor_idx,"sepal width (cm)"]
           ,example_y[versicolor_idx],label="versicolor",color="red")

ax2=f.add_subplot(122,projection="3d")

x_range=np.linspace(example_X.values[:,0].min(),example_X.values[:,0].max(),100)
y_range=np.linspace(example_X.values[:,1].min(),example_X.values[:,1].max(),100)
x_range, y_range = np.meshgrid(x_range, y_range)
z_range=x_range+y_range

ax2.plot(x_range,y_range,z_range,color="green")
plt.show()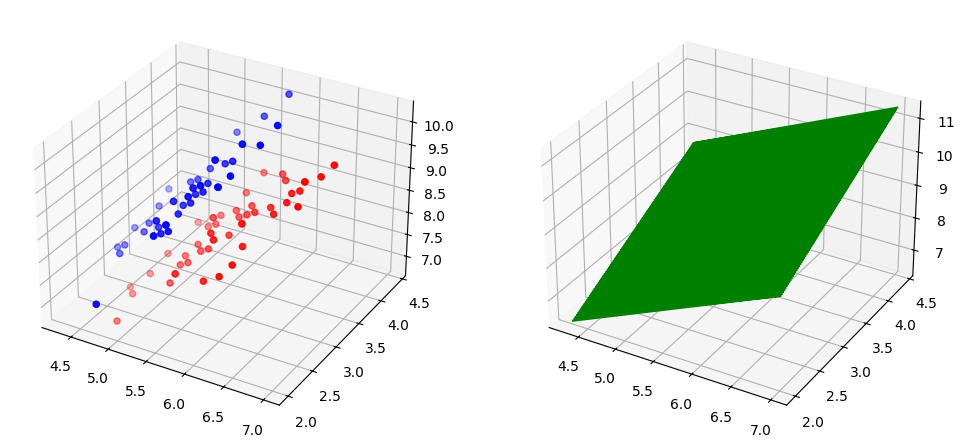

직선으로 투영시킨다면서 왜 평면을 그려지는 벡터 $w=(1,1)$을 통해 각 클래스의 데이터 세트가 어떤 값인지 보여지기 위해서 표현했기 때문입니다.

즉, LDA는 위에서 $z$축의 값에 초점이 맞춰져있습니다.

---

LDA 과정

위의 데이터 세트를 임의의 직선으로 투영시키는 과정을 보면서 우리가 생각해야하는 문제는 다음과 같습니다.

"어떤 직선이 이진분류를 위해 가장 적절할까?"

이 질문의 답을 위해서 다음과 같이 가정하겠습니다.

1. 데이터 세트 $D=\{(x_i,y_i)\}_{i=1}^{m}| y_i\in \{0,1\}$ 를 가정하겠습니다.

2. $X_j, \mu_j, \sum_{j}$는 각각 $y_i=j \in \{0,1\}$ 인 클래스의 집합, 해당 집합의 평균벡터, 공분산행렬 입니다.

위의 가정을 통해 다음과 같이 계산할 수 있습니다.

1. $\mu_j$ 는 직선 $w$위에 투영시키면(위에서의 $z$축에 해당) $w^Tu_j$ 입니다.

2. $\sum_j$는 $w^T \sum_jw$ 로 투영됩니다.

3. 위의 각각의 값은 모두 실수입니다.($z$축으로 이해하면 편합니다.)
   
   

2. 공분산 투영 유도

위의 $\sum_j$의 투영값을 유도하기 위해선 공분산에 대한 이해가 필요합니다.

공분산은 다음과 같이 정의됩니다.

이를 기반으로 공분산행렬은 다음과 같이 정의됩니다.

데이터 세트 $D=(x_i)_{i=1}^{m}$ 에 대해 $x_i=(d_{i1},d_{i2},...,d_{it})$라고 가정하겠습니다.

따라 다음과 같이 치환하겠습니다.

$D=(d_1,d_2,...,d_t)$

공분산행렬은 다음과 같이 나타낼 수 있습니다.

임의의 직선 $w=(w_1,w_2,...,w_t)$ 에 대해 투영된 집합 $X_j$의 분산 $var(X_j)$는 다음과 같습니다.

여기서 위의 공분산 행렬의 정의에 따라 다음과 같습니다.

(단순 행렬곱이니 직접 해보시길 추천드립니다.)

이제 LDA에서 요구하는 최적의 직선은 다음과 같음을 이해할 수 있습니다.

1. 집단내 투영점들의 밀집도가 높아야합니다.따라서 다음 값을 최소로 만들어야 합니다.

   $w^T\sum_0w+w^T\sum_1w$

2. 집단간 중심점 사이의 거리가 멀어져야합니다. 따라서 아래의 값을 최대로 해야합니다.

   $||w^T\mu_0-w^T\mu_1||^2$

   ($2-norm$ 값을 사용합니다.)

따라서 아래의 값을 최대로 하면 됩니다.

---

LDA 해찾기

우리는 $J$의 값을 최대로 하면 됨을 위의 과정을 통해 알았습니다.
이제 이를 만족하는 직선$w$를 찾아보죠.

$J$의 값을 보면 당연하게도 $||w||^2$ 는 중요하지않습니다.
따라서 다음과 같은 가정을 할 수 있습니다.

우리가 찾던 직선 $\hat w$ 에 대해서 다음과 같습니다.

결국, 우리는 아래를 만족하는 $w=\alpha \hat w$ 를 찾습니다.

,such that $w^T\sum_0w+w^T\sum_1w=1$

위의 $w$는 라그랑주 승수법과 특이값 분해를 이용해 구할 수 있는데,

1. 라그랑주 승수법에 의해 다음을 만족합니다.

   $\exist \lambda \in \real , ||\mu_0-\mu_1||^2w=\lambda(\sum_0+\sum_1)w$

2. 따라서 다음과 같이 정리할 수 있습니다.

   $||\mu_0-\mu_1||^2w=(\mu_0-\mu_1)(\mu_0-\mu_1)^Tw=\alpha(\mu_0-\mu_1)$

3. 위의 식을 기존의 식에 대입하면 다음과 같습니다.

   $w=\lambda'(\sum_0+\sum_1)^{-1}(\mu_0-\mu_1)$

4. 일반적으로 $(\sum_0+\sum_1)^{-1}$은 특이값 분해를 이용해 계산합니다.

---

3. 코드로 알아보기

위의 과정과는 다르게 sklearn 모듈을 이용하면 간단하게 구현할 수 있습니다.

from sklearn import discriminant_analysis as dis
LDA=dis.LinearDiscriminantAnalysis(solver="svd",n_components=1)
LDA.fit(example_X,named_y.values.ravel())

이렇게 학습시킨 LDA에서 찾은 해, 즉 직선은 다음과 같이 확인할 수 있습니다.

w=LDA.coef_
b=LDA.intercept_
print("w :",w)
print("b :",b)

또한 파라미터 solver를 lsqr로 바꾸면 위의 해를 특이값분해(svd) 방법이 아닌 최소자승법(least-square method)로 찾습니다.

결과를 확인해보겠습니다.

# 결정된 직선
def calculate(X):
    return X@LDA.coef_.T+LDA.intercept_
    
idx1=named_y[named_y=="setosa"].dropna().index
idx2=named_y[named_y=="versicolor"].dropna().index
col_name=example_X.columns

#클래스별 평균벡터와 데이터의 직선으로의 투영값
point1=calculate(example_X.loc[idx1,col_name].mean())
point2=calculate(example_X.loc[idx2,col_name].mean())

class1=calculate(example_X.loc[idx1,col_name])
class2=calculate(example_X.loc[idx2,col_name])

#시각화
x_range=np.linspace(-20,20,500)

plt.plot(x_range,x_range,linestyle="--",color="C7")
plt.scatter(class1,class1,color="C9",label="setosa")
plt.scatter(class2,class2,color="C1",label="versicolor")
plt.scatter(point1,point1,color="C3",marker="o",label="setosa 중심점")
plt.scatter(point2,point2,color="C2",marker="o",label="versicolor 중심점")
plt.legend()
plt.grid()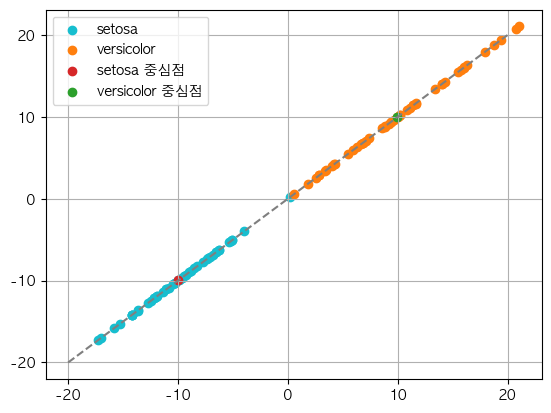

위와 같이 $y=(1,1)x$ 직선을 이용해 각 투영된 클래스별 데이터 샘플의 분포를 표현했습니다.