contents
- 분류분석 - 로지스틱회귀
- 분류 평가 지표
- (실습) 로지스틱회귀
- 로지스틱회귀 정리
summary
- 분류분석 - 로지스틱회귀
🛳️타이타닉 생존 분류 문제
https://www.kaggle.com/c/titanic
-
여성은 모두 생존, 남성은 모두 사망으로 판별한다면?
- 정확도: 78.6% (여성 생존 233 + 남성 사망 468) / 전체 인원 891
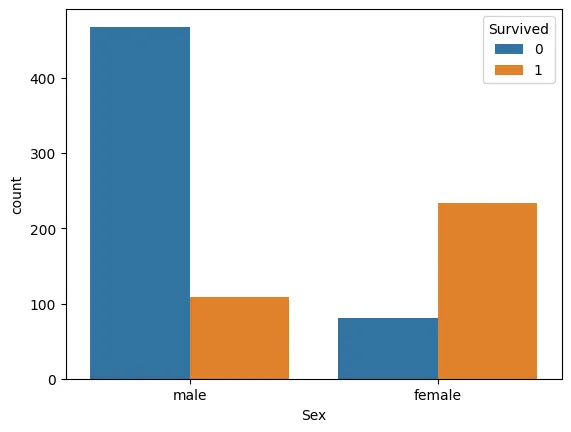
->모델을 만들지 않고도 무려 80%에 가까운 정확도를 만들다니 엄청난 인사이트! 그러나 추가적 도구를 활용해 정확도의 수치를 높힐 수 있다! -
로지스틱회귀 이론
☑️ 범주형 Y에서 선형함수의 한계
X가 연속형 변수이고, Y가 특정 값이 될 확률이라고 설정한다면, 선형으로 설명하긴 쉽지 않다. 확률은 0과 1사이 인데, 예측 값이 확률 범위를 넘어갈 수 있는 문제가 발생!
그래서 S자 형태의 함수를 적용하면 잘 설명한다고 할 수 있을 것이다.
-Y가 0,1 범주형인 경우 함수 적합
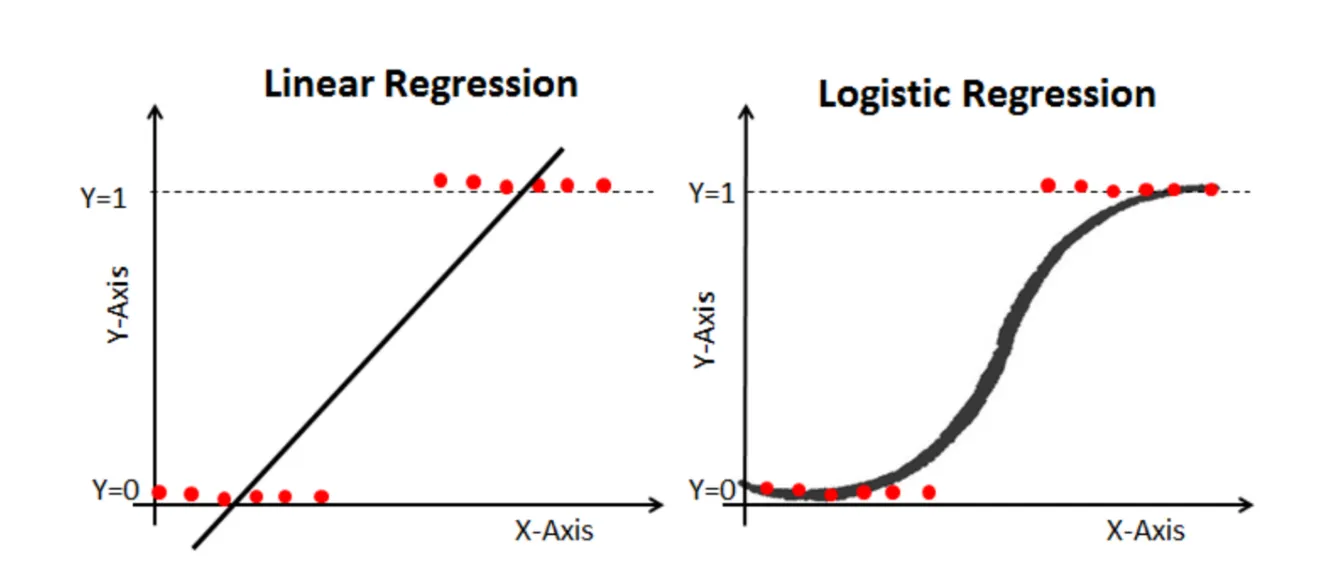
☑️ 로짓의 개념의 등장
📌위 S형태의 함수를 만들기 위해서 오즈비(Odds ratio)의 개념을 적용.
승산비라 불리는 오즈비는 실패확률 대비 성공확률로, 도박사들이 자주 쓰는 개념.
예를 들어 도박이 성공할 확률이 80% 라면, 오즈비는 80%/20% = 4 예요. 다시 해석해보면 1번 실패하면 4번은 딴다는 말.
하지만 오즈비는 바로 쓸 수 없다. P는 확률 값으로 0,1사이 값인데, P가 증가할수록 오즈비가 급격하게 증가하기 때문에 너무 확률이 급격하게 증가하고 선형성을 따르지 않게 된다. 따라서 로그를 씌워 이 부분을 좀 완화하기로 한다.
- 오즈비와 확률의 관계 / 로짓과 확률의 관계
- 로짓의 그래프가 더 선형적인 그림을 나타내어 선형회귀의 기본식을 활용할 수 있게 됨
- 로지스틱”회귀”라고 불리는 이유가 이것
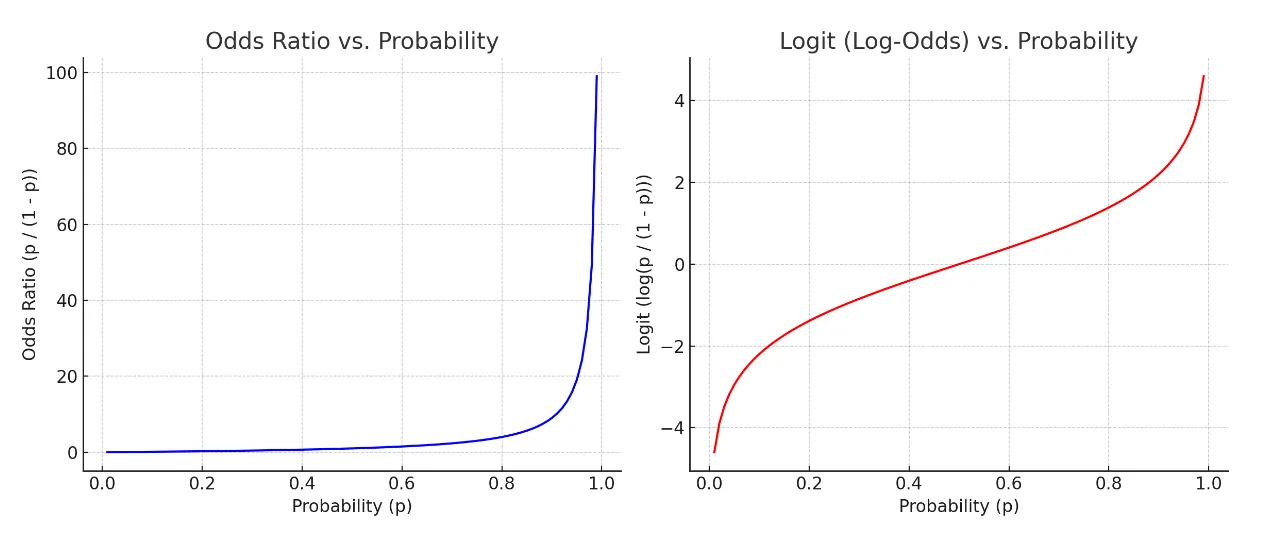 확률이 증가할수록 (좌)오즈비는 급격히 발산, (우) 로짓은 완만하게 증가
확률이 증가할수록 (좌)오즈비는 급격히 발산, (우) 로짓은 완만하게 증가
- 위 그래프의 확률 - 로짓 그래프 X-Y축을 교체
- 로지스틱 함수
📌로지스틱 함수는 시그모이드 함수 중 하나로 딥러닝에서 다시 활용된다. 값을 계산하면 확률 도출 된다는 것만 기억
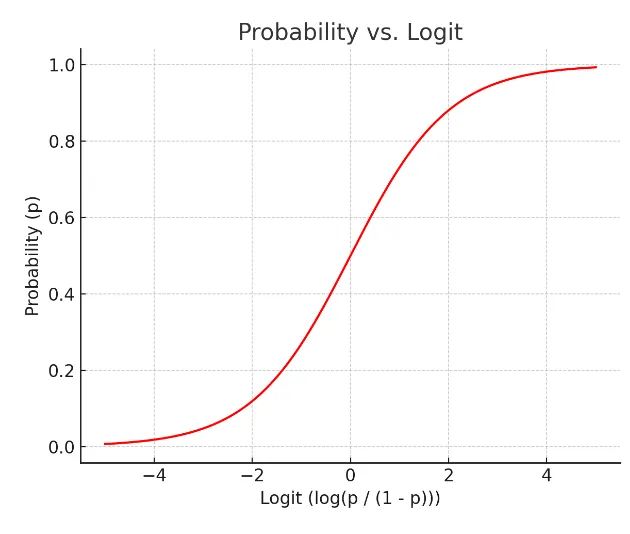
📌로짓의 장점은 어떤 값을 가져오더라도 반드시 특정 사건이 일어날 확률(Y값이 특정 값일 확률)이 0과 1안으로 들어오게 하는 특징을 가지게 된다.
- 로지스틱 함수
- 로짓과 기존 선형회귀의 우변을 합쳐 다음과 같은 식을 도출양변에 자연지수 를 취하면
- 해석: X값이 만큼 증가하면 오즈비는 만큼 증가한다.
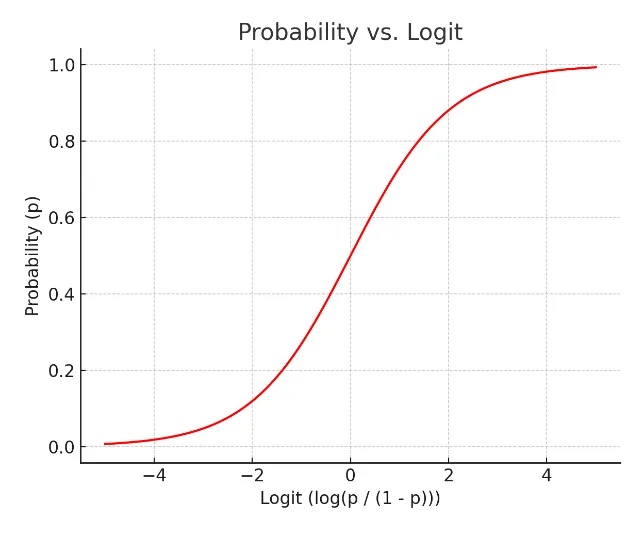
📌로지스틱함수는 가중치 값을 안다면 X값이 주어졌을 때 해당 사건이 일어날 수 있는 P의 확률을 계산할 수 있다.
이때, 확률 0.5를 기준으로 그보다 높으면 사건이 일어남(P(Y) = 1), 그렇지 않으면 사건이 일어나지 않음(P(Y) = 0)으로 판단하여 분류 예측에 사용.
- 분류 평가 지표
- 정확도와 F1 - Score
☑️ 정확도의 한계
예시)모든 환자를 정상이라고 판정하는 “암 예측 모델” - 암 예측 모델: 무조건 환자가 음성(정상인)이라고 판정
- 100명의 환자 입실, 95명은 음성(정상), 5명은 양성(암 환자)
- 위에 따르면 암 예측 모델의 정확도는 95%
->정확도는 매우 높은 것 같지만 실제로 양성(암 환자)는 하나도 못 맞춤. 이런 사기를 잘 걸러내기 위한 지표를 만들어보자.
☑️ 혼동 행렬(confusion Matrix)
:실제 값과 예측 값에 대한 모든 경우의 수를 표현하기 위한 2x2 행렬
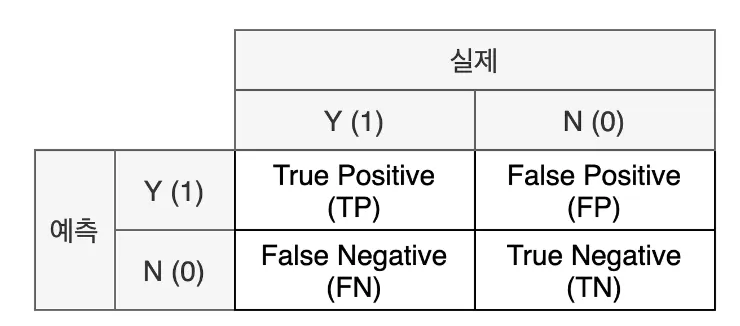
- 표기법
- 실제와 예측이 같으면 True / 다르면 False
- 예측을 양성으로 했으면 Positive / 음성으로 했으면 Negative
- 해석
- TP: 실제로 양성(암 환자)이면서 양성(암 환자) 올바르게 분류된 수
- FP: 실제로 음성(정상인)이지만 양성(암 환자)로 잘못 분류된 수
- FN: 실제로 양성(암 환자)이지만 음성(정상인)로 잘못 분류된 수
- TN: 실제로 음성(정상인)이면서 음성(정상인)로 올바르게 분류된 수
- 지표
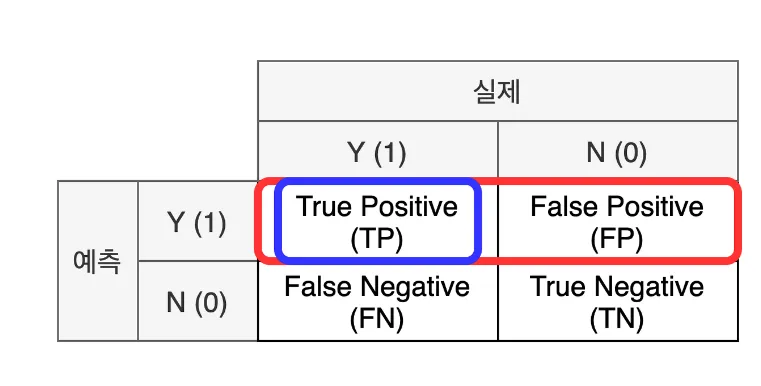
1) 정밀도(Precision): 모델이 양성 1로 예측한 결과 중 실제 양성의 비율(모델의 관점)
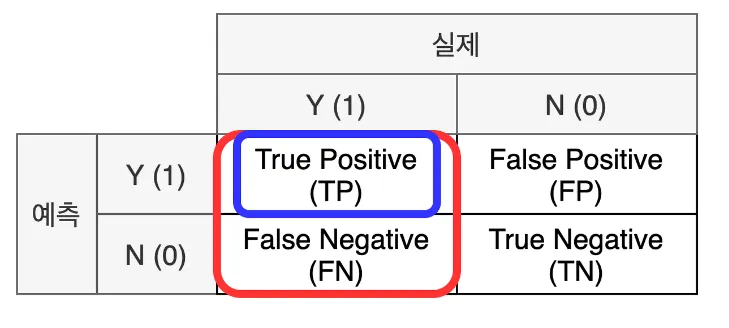
 2)재현율(Recall): 실제 값이 양성인 데이터 중 모델이 양성으로 예측한 비율(데이터의 관점)
2)재현율(Recall): 실제 값이 양성인 데이터 중 모델이 양성으로 예측한 비율(데이터의 관점)
 3) f1-Score: 정밀도와 재현율의 조화 평균4)정확도(Accuracy)
3) f1-Score: 정밀도와 재현율의 조화 평균4)정확도(Accuracy) - 실제 적용
- TP: 실제로 양성(암 환자)이면서 양성(암 환자) 올바르게 분류된 수 → 0명
- FP: 실제로 음성(정상인)이지만 양성(암 환자)로 잘못 분류된 수 → 0명
- FN: 실제로 양성(암 환자)이지만 음성(정상인)이라고 분류된 수 → 5명
- TN: 실제로 음성(정상인)이면서 음성(정상인)이라고 분류된 수 → 95명
- 정밀도는 정의되지 않음(divsion by zero), 재현율은 0
- 결과적으로 f1-score는 0
📌위처럼 정확도가 제 기능을 못하는 때는 분류에서 특히 Y값이 unbalance하지 못할 때 일어난다. 따라서 이를 위해서 Y 범주의 비율을 맞춰주거나 평가 지표를 f1 score을 사용함으로써 이를 보완한다.
- (실습) 로지스틱회귀
☑️ 자주 쓰는 함수
sklearn.linear_model.LogisticRegression: 로지스틱회귀 모델 클래스- 속성
classes_: 클래스(Y)의 종류n_features_in_: 들어간 독립변수(X) 개수feature_names_in_: 들어간 독립변수(X)의 이름coef_: 가중치intercept_: 바이어스
- 메소드
fit: 데이터 학습predict: 데이터 예측predict_proba: 데이터가 Y = 1일 확률을 예측
- 속성
sklearn.metrics.accuracy: 정확도sklearn.metrics.f1_socre: f1_score
☑️ 타이타닉 실습
1) 로지스틱회귀 모델 불러오고 훈련하기
titaninc_df.head(3)
- 필요한 데이터만 뽑기
# info(): 데이터에 대한 결측치, 데이터전체 갯수 등을
titaninc_df.info()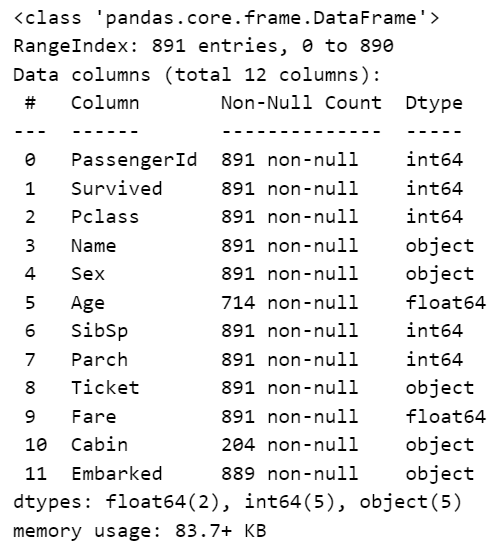
-
숫자
- Age, SibSp,Parch, Fare
-
범주형
- Pclass, Sex, Cabin, Embarked
-
X변수 1개, Y변수(Survived)
# X변수: Fare, Y변수: Survived
X_1 = titaninc_df[['Fare']]
y_true = titaninc_df[['Survived']]
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LogisticRegression
model_lor = LogisticRegression()
model_lor.fit(X_1, y_true)
2) 변수
- 1차 모델: Fare
sns.scatterplot(titaninc_df, x = 'Fare', y = 'Survived')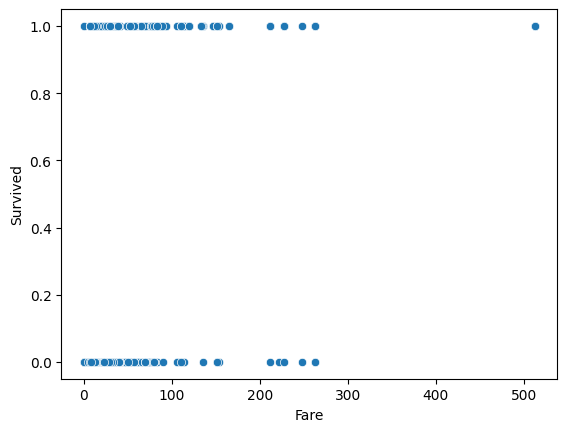
산점도보다 히스토 그램으로 분산을 확인하는 것이 더 좋을 듯 싶다
sns.histplot(titaninc_df, x = 'Fare')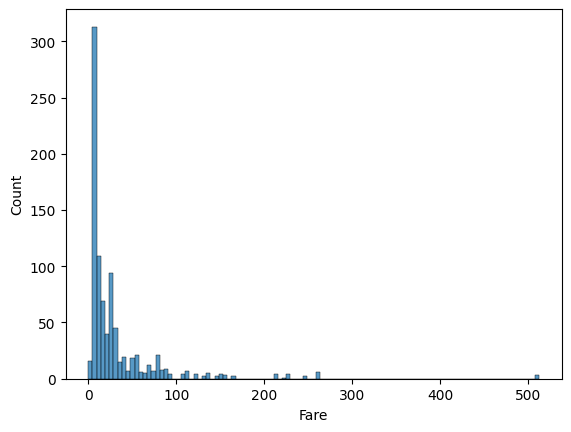
# 데이터 기술통계를 보는법(수치형) describe()
titaninc_df.describe()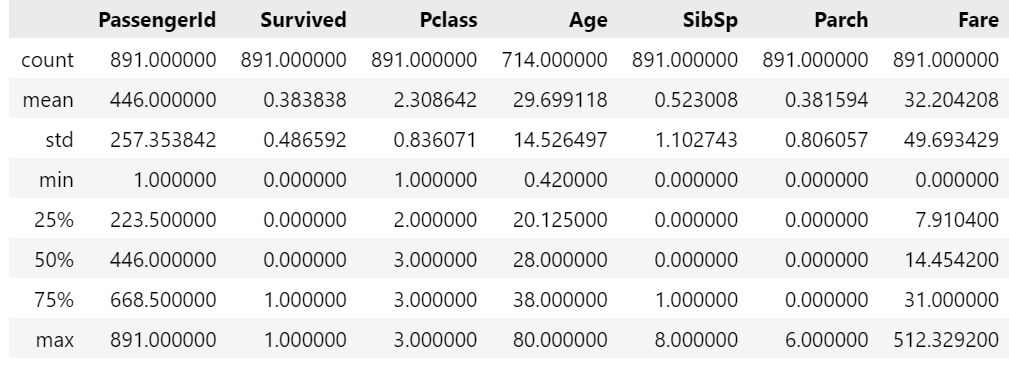
def get_att(x):
#x모델을 넣기
print('클래스 종류', x.classes_)
print('독립변수 갯수', x.n_features_in_)
print('들어간 독립변수(x)의 이름',x.feature_names_in_)
print('가중치',x.coef_)
print('바이어스', x.intercept_)
get_att(model_lor)클래스 종류 [0 1]
독립변수 갯수 1
들어간 독립변수(x)의 이름 ['Fare']
가중치 [[0.01519666]]
바이어스 [-0.94131796]
from sklearn.metrics import accuracy_score, f1_score
def get_metrics(true, pred):
print('정확도', accuracy_score(true, pred))
print('f1-score', f1_score(true, pred))
y_pred_1 = model_lor.predict(X_1)
y_pred_1[:10]
len(y_pred_1)891
get_metrics(y_true, y_pred_1)정확도 0.6655443322109988
f1-score 0.35497835497835495
- 2차 모델: Pclass, Sex, Fare
다중로스틱회귀
-
숫자
- Age, SibSp,Parch, Fare
-
범주형
- Pclass, Sex, Cabin, Embarked
-
X변수 개, Y변수(Survived)
#Y(Surivved): 사망
#X(수치형): Fare
#X(범주형): Plcass(좌석등급), Sex
def get_sex(x):
if x == 'female':
return 0
else:
return 1
titaninc_df['Sex_en'] = titaninc_df['Sex'].apply(get_sex)
titaninc_df.head(3)
X_2 = titaninc_df[['Pclass','Sex_en','Fare']]
y_true = titaninc_df[['Survived']]
model_lor_2 = LogisticRegression()
model_lor_2.fit(X_2,y_true)
get_att(model_lor_2)클래스 종류 [0 1]
독립변수 갯수 3
들어간 독립변수(x)의 이름 ['Pclass' 'Sex_en' 'Fare']
가중치 [[-8.88331324e-01 -2.53993425e+00 1.64019087e-03]]
바이어스 [3.02004403]
y_pred_2 = model_lor_2.predict(X_2)
y_pred_2[:10]y_pred_2 = model_lor_2.predict(X_2)
y_pred_2[:10]
y_pred_1[:10]array([0, 1, 0, 0, 0, 0, 0, 0, 0, 0], dtype=int64)
3) 평가하기
1. accuracy
2. f1_score
# X변수가 Fare
get_metrics(y_true, y_pred_1)
# X변수가 Fare, Pclass, Sex
get_metrics(y_true, y_pred_2)정확도 0.6655443322109988
f1-score 0.35497835497835495
정확도 0.7867564534231201
f1-score 0.7121212121212122
# 각 데이터별 Y=1인 확률 뽑아내기(생존할 확률)
model_lor_2.predict_proba(X_2)array([[0.8977979 , 0.1022021 ],
[0.09546762, 0.90453238],
[0.40901264, 0.59098736],
...,
[0.40287202, 0.59712798],
[0.58880217, 0.41119783],
[0.89772263, 0.10227737]])
y_pred_2[:10]array([0, 1, 1, 1, 0, 0, 0, 0, 1, 1], dtype=int64)
- 로지스틱회귀 정리
-
로지스틱회귀
- 장점: 역시 직관적이며 이해하기 쉽다.
- 단점: 복잡한 비선형 관계를 모델링 하기 어려울 수 있음
- Python 패키지
-sklearn.linear_model.LogisticRegressoninsight
-
F1 스코어와 변수 중요도
F1 스코어는 모델의 예측 성능(정밀도와 재현율의 조화)을 나타낸다.
특정 변수가 F1 스코어에 얼마나 기여하는지는 변수 간의 상관관계, 데이터 분포, 모델의 학습 방법에 따라 다르다.
따라서, 단순히 회귀 계수의 크기로 F1 스코어에 어떤 변수가 가장 큰 영향을 미치는지 직접적으로 판단할 수는 없다.
그리고 추가적으로 f1score를 높이고 싶다면 GridSearchCV를 사용해 로지스틱 회귀의 하이퍼파라미터(C 값)를 최적화하면 F1 스코어를 높일 수 있다!
from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import f1_score
# 하이퍼파라미터 튜닝
param_grid = {'C': [0.01, 0.1, 1, 10, 100]}
grid = GridSearchCV(LogisticRegression(max_iter=1000), param_grid, scoring='f1', cv=5)
grid.fit(X_train, y_train)
# 최적의 모델로 예측
best_model = grid.best_estimator_
y_pred = best_model.predict(X_test)
# F1 스코어 출력
f1 = f1_score(y_test, y_pred)
print(f"Best F1 Score: {f1:.4f}")+교차 검증과 특성 선택
:변수 선택을 자동화하려면 RFE (Recursive Feature Elimination) 같은 기법을 사용할 수 있다.
from sklearn.feature_selection import RFE
# 로지스틱 회귀 모델과 RFE
model = LogisticRegression(max_iter=1000)
rfe = RFE(model, n_features_to_select=5) # 중요 변수 5개 선택
rfe.fit(X_train, y_train)
# 선택된 변수
print("Selected Features:", X_train.columns[rfe.support_])