[머신러닝]머신러닝의 이해와 라이브러리 활용 심화_데이터분석 프로세스

Arin lee·2024년 11월 19일
TIL머신러닝
0

contents

  • 예측모델링 프로세스
    • 데이터 수집
    • 탐색적 데이터 분석(EDA)
    • 데이터 전처리
    • (실습) 탐색적 데이터분석과 데이터전처리
    • 데이터 분리
    • (실습) 데이터 전체 프로세스적용
    • 교차 검증과 GridSearch

summary

  • 예측모델링 프로세스
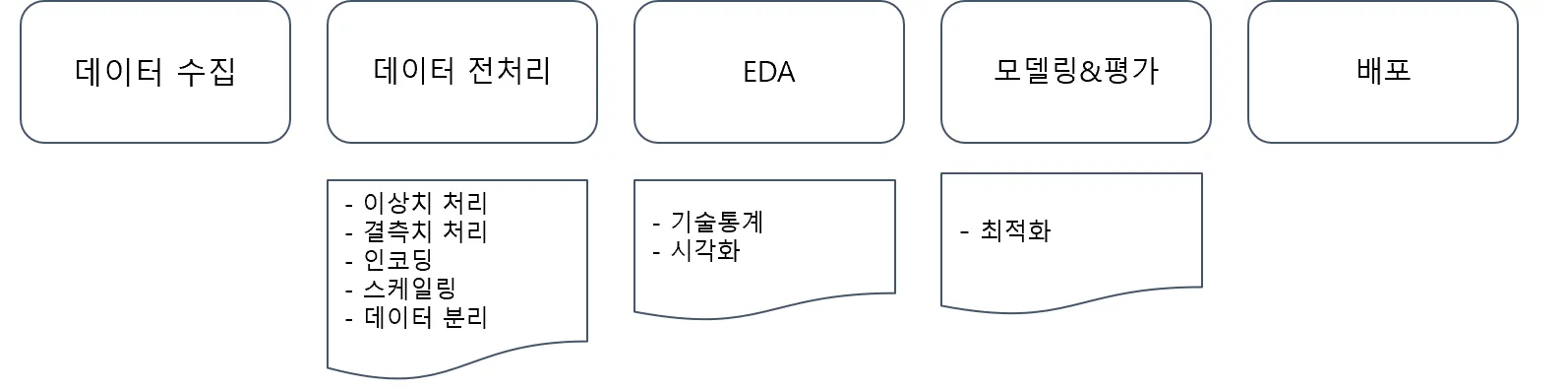
  1. 데이터 수집
    ☑️ 데이터 수집에 따른 프로세스
    📌실제로 데이터를 수집하려면 개발을 통해 데이터를 적재하고 수집하는 데이터 엔지니어링 역량이 필요한데, 이 부분은 개발자가 직접 설계하고 저장하게 된다. 데이터 분석가는 이미 존재하는 데이터를 SQL 혹은 Python 로 통해 추출하고 리포팅 혹은 머신러닝을 통한 예측을 담당.

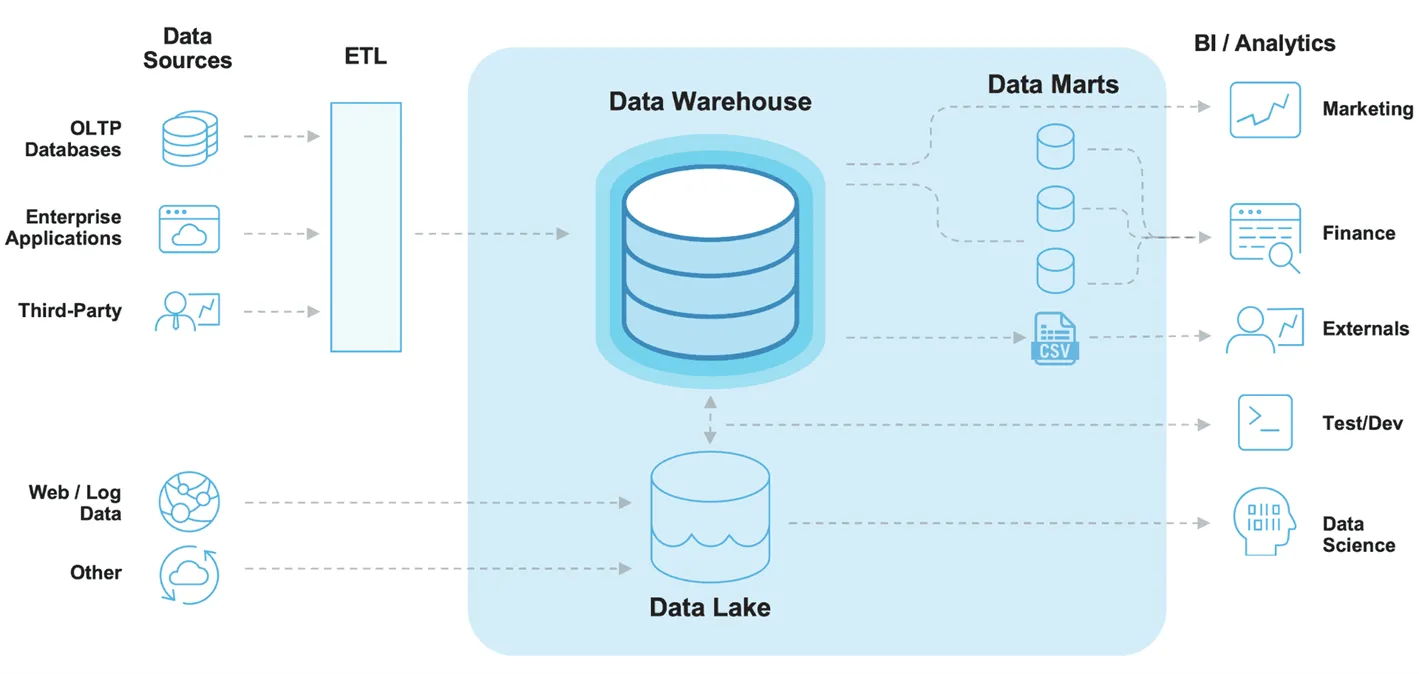
    1) Data Source
    - OLTP Database: OnLine Transaction Processing 은 온라인 뱅킹,쇼핑, 주문 입력 등 동시에 발생하는 다수의 트랜잭션(데이터베이스 작업의 단위) 처리 유형
    - Enterprise Applications: 회사 내 데이터 (ex 고객 관계 데이터, 제품 마케팅 세일즈)
    - Third - Party: Google Analytics와 같은 외부소스에서 수집되는 데이터
    - Web/Log: 사용자의 로그데이터
    2) Data Lake: 원시 형태의 다양한 유형의 데이터를 저장
    3) Data Warehouse: 보다 구조화된 형태로 정제된 데이터를 저장
    4) Data Marts: 회사의 금융, 마케팅, 영업 부서와 같이 특정 조직의 목적을 위해 가공된 데이터
    5) BI/Analytics: business Intelligence(BI)는 의사결정에 사용될 데이터를 수집하고 분석하는 프로세스

☑️ 실제 데이터 수집

  • 회사 내 데이터가 존재한다면
    • SQL 혹은 Python 을 통해 데이터 마트를 생성
  • 회사 내 Data가 없다면 → 데이터 수집 필요
    • 방법1: CSV, EXCEL 파일 다운로드
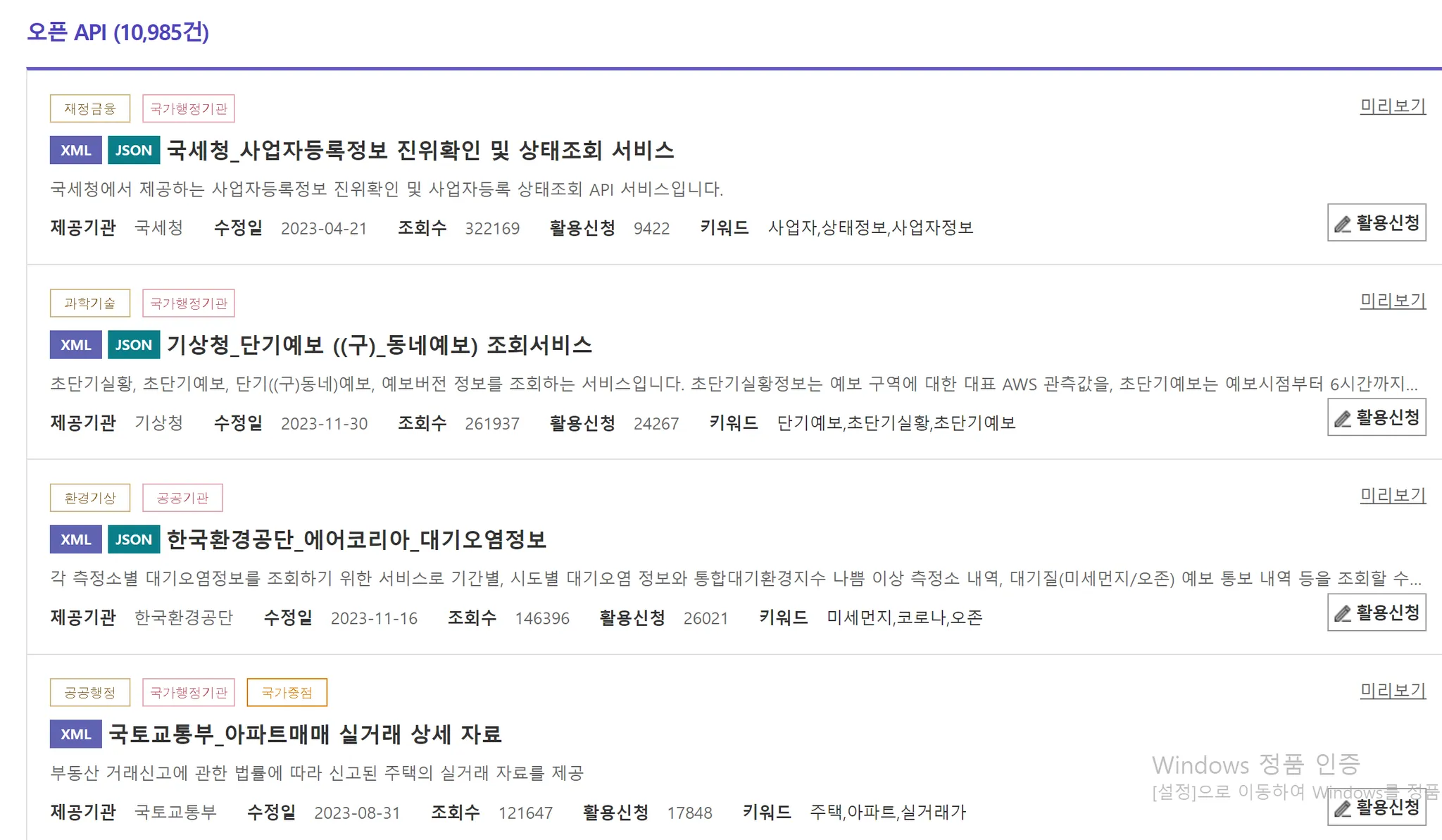
    • 방법2: API를 이용한 데이터 수집
    • 방법3: Data Crawling
  1. 탐색적 데이터 분석(EDA)
    :탐색적 데이터 분석(Exploratory Data Analysis, EDA)는 데이터의 시각화, 기술통계 등의 방법을 통해 데이터를 이해하고 탐구하는 과정
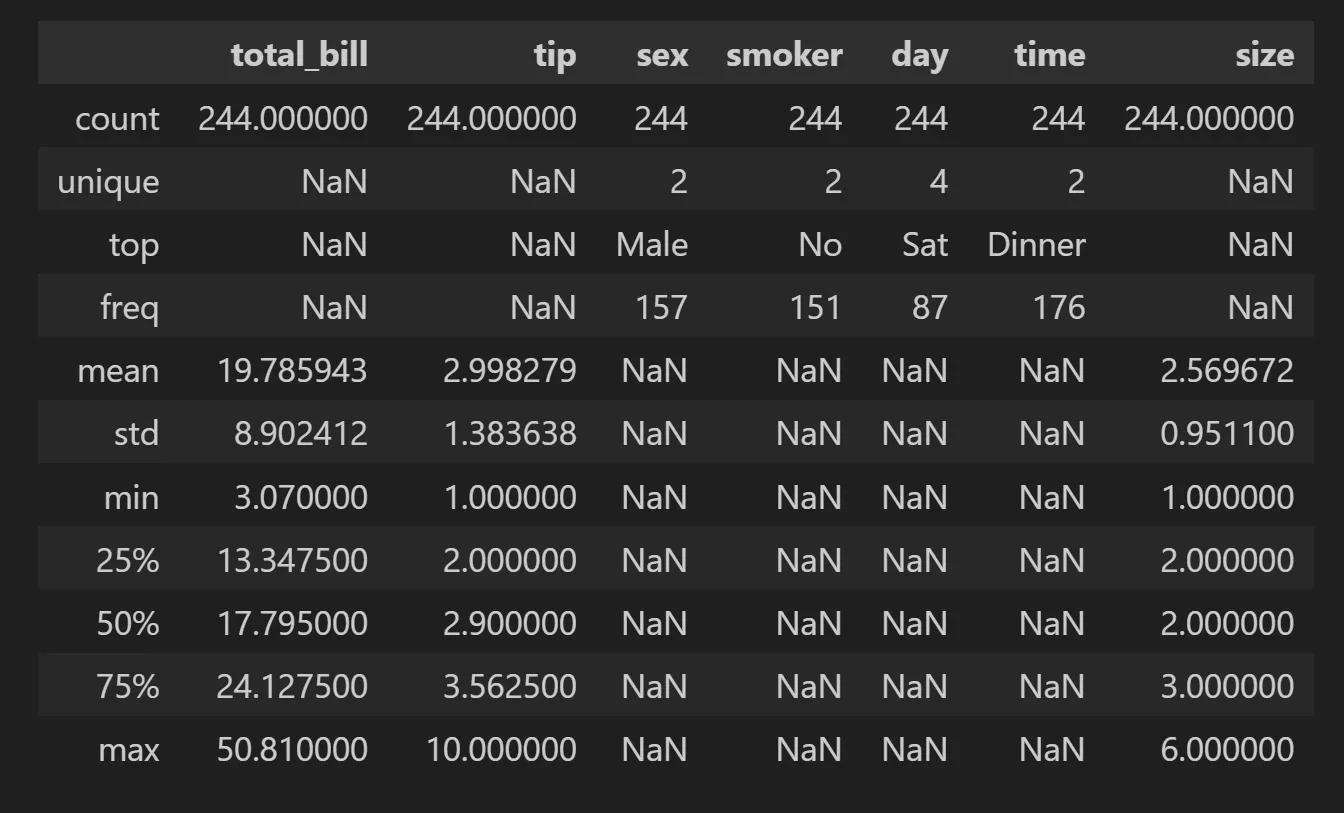
    ☑️ 기술통계를 통한 EDA 예시
  • tips.describe()
    - include='all' 옵션을 통해 범주형 데이터도 확인 가능

    ☑️ 시각화를 이용한 EDA 예시
    tips 데이터

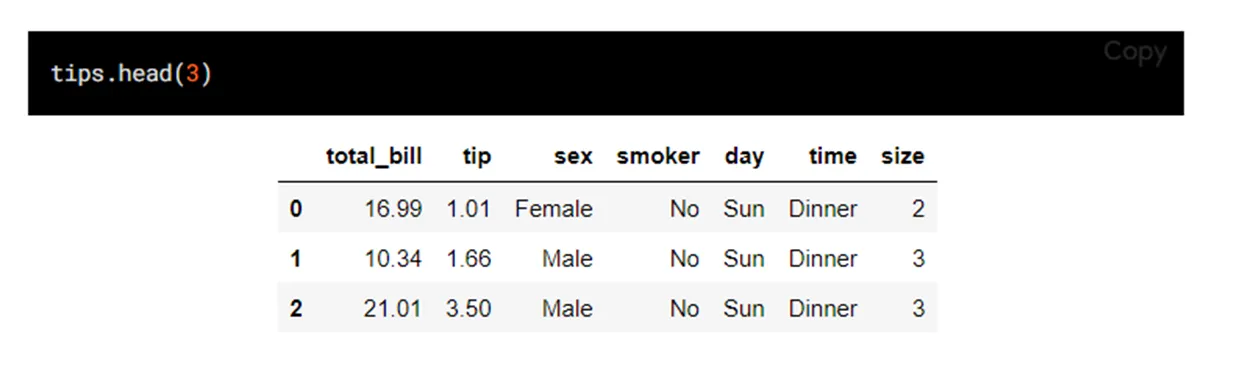
    1) countplot: 범주형 자료의 빈도 수 시각화
    - 방법: 범주형의 데이터의 각 카테고리별 빈도수를 나타낼 때
    - Ex) 상점에서 판매되는 제품의 카테고리별 판매수 파악
    - x축: 범주형 자료
    - y축: 자료의 빈도수

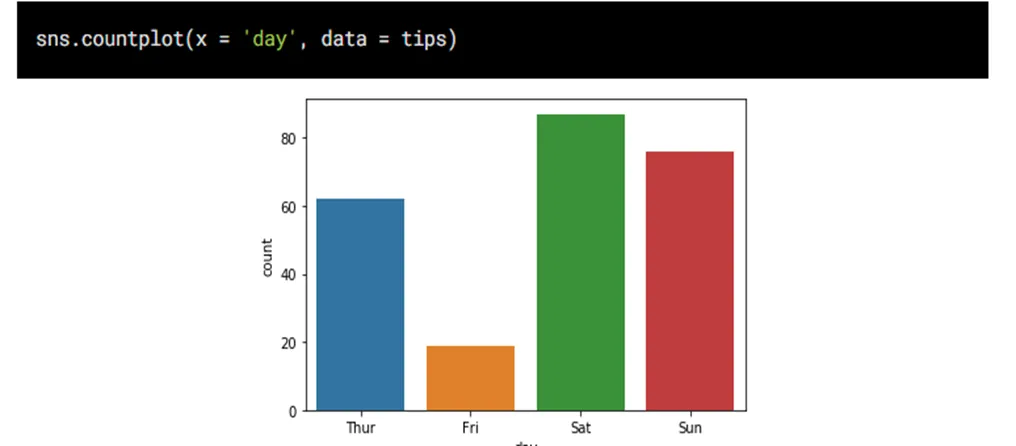
    2) barplot: 범주형 자료의 시각화
    - 방법: 범주형 데이터의 각 카테고리에 따른 수치 데이터의 평균을 비교
    - Ex) 다양한 연령대별 평균소득을 비교할 때
    - x축: 범주형 자료
    - y축: 연속형 자료

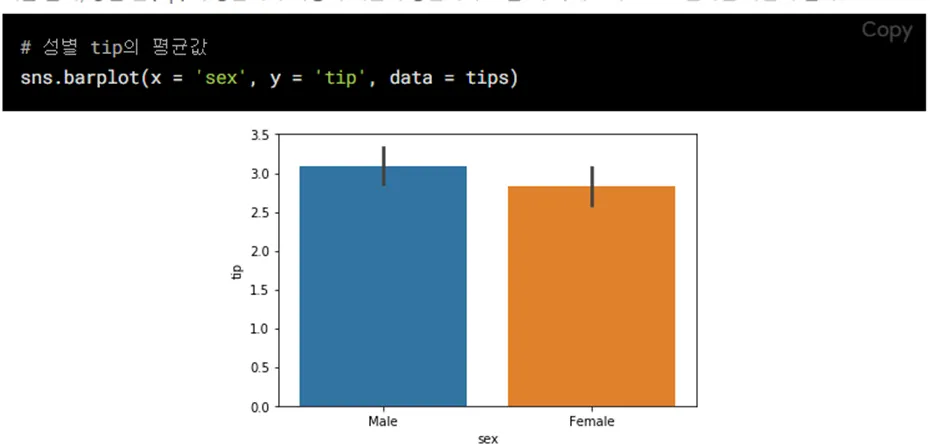
    3) boxplot: 수치형 & 범주형 자료의 시각화
    - 방법: 데이터의 분포, 중앙값, 사분위 수, 이상치 등을 한눈에 표현하고 싶을 때
    - Ex) 여러 그룹간 시험 점수 분포를 비교할 때
    - x: 수치형 or 범주형
    - y: 수치형 자료

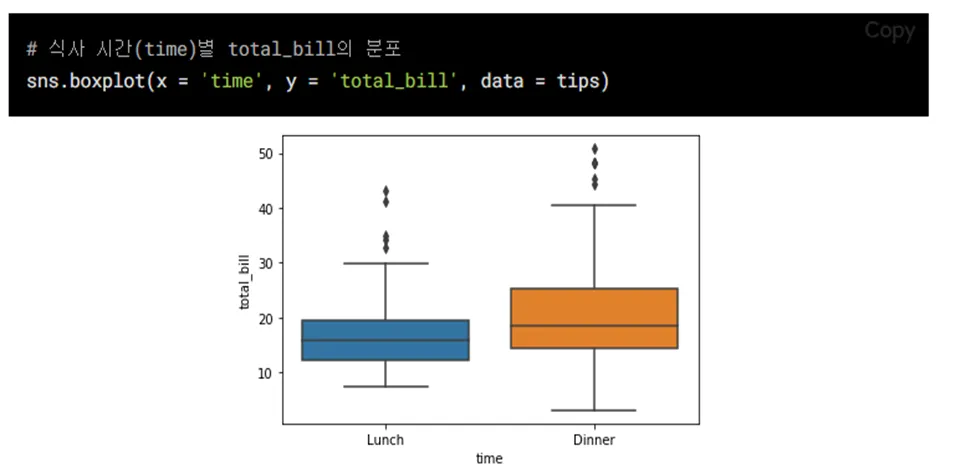
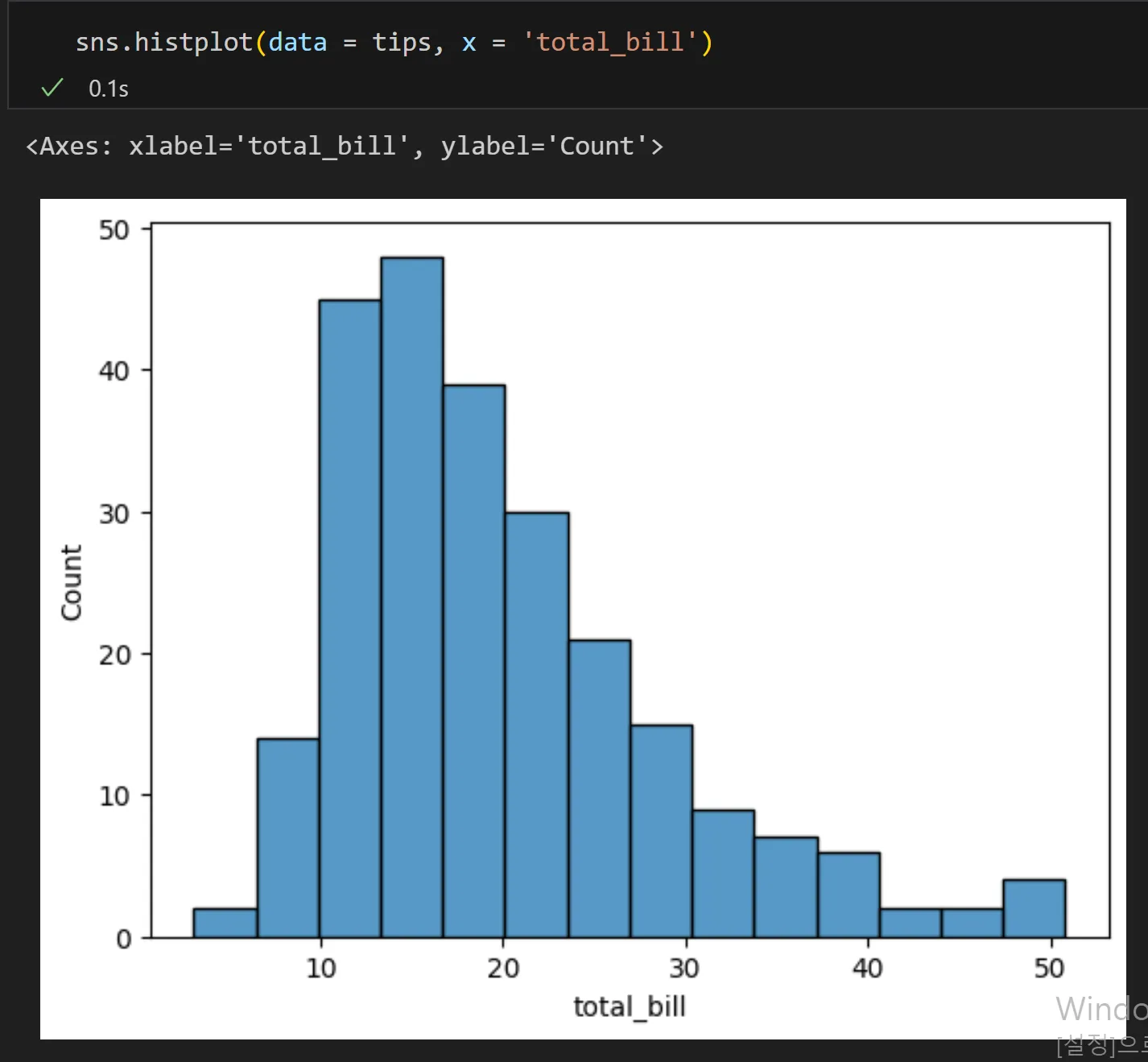
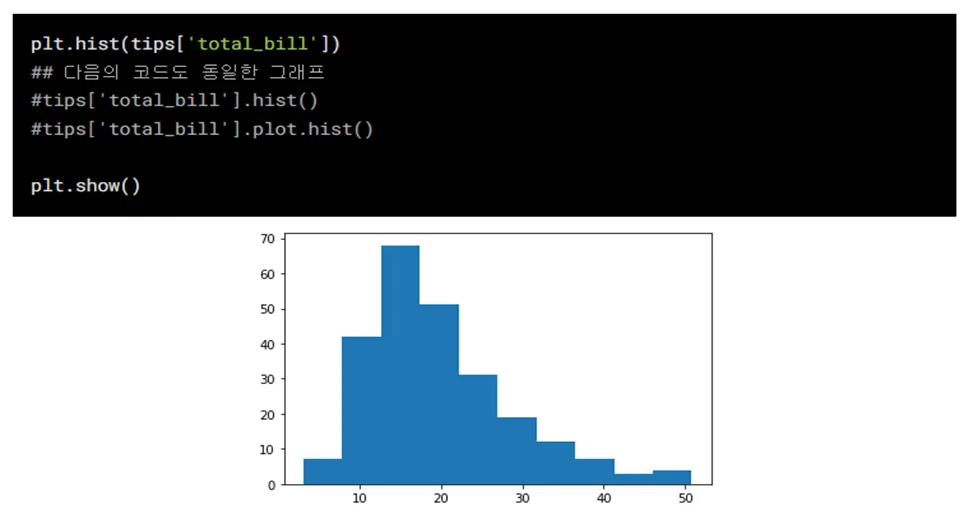
    4) histogram: 수치형 자료 빈도 시각화
    - 방법: 연속형 분포를 나타내고 싶을 때, 데이터가 몰려있는 구간을 파악하기 쉬움
    - Ex)고객들의 연령 분포를 파악 할 때
    - x축: 수치형 자료
    - y축: 자료의 빈도수

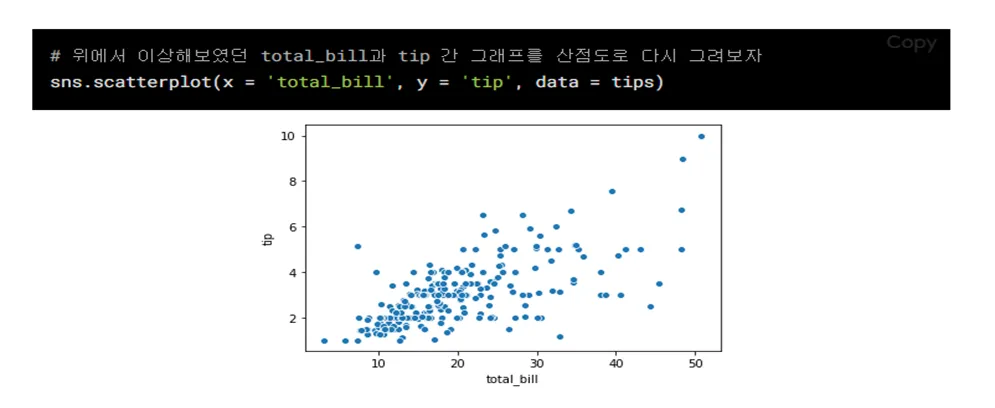
    5)scatterplot: 수치형끼리 자료의 시각화
    - 방법: 두 연속형 변수간의 관계를 시각적으로 파악하고 싶을 때
    - Ex) 키와 몸무게 간의 관계를 나타낼 때
    - x축: 수치형 자료
    - y축: 수치형 자료

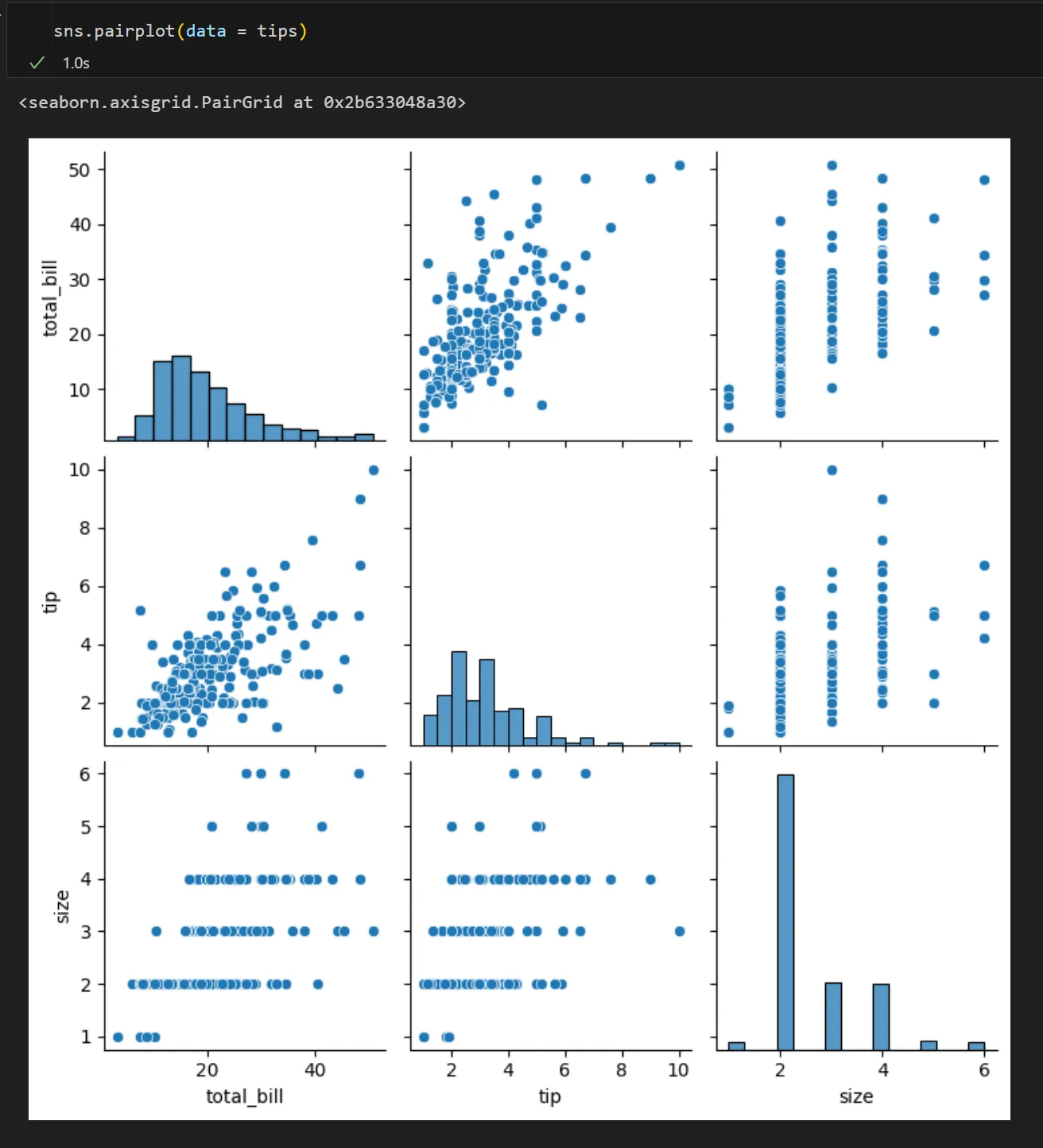
    6)pairplot: 전체 변수에 대한 시각화
    - 방법: 한 번에 여러 개의 변수를 동시에 시각화 하고 싶을 때
    - x축: 범주형 or 수치형 자료
    - y축: 범주형 or 수치형 자료
    - 대각선: 히스토그램(분포)
  1. 데이터 전처리
    전체 분석 프로세스에서 90%를 차지 할 정도로 노동, 시간 집약적인 단계
    ☑️ 이상치(Outlier)
    📌이상치(Outlier)란 보통 관측된 데이터 범위에서 많이 벗어난 아주 작은 값 혹은 큰 값
    1) Extreme Studentized Deviation(ESD) 이용한 이상치 발견
  • 데이터가 정규분포를 따른다고 가정할 때, 평균에서 표준편차의 3배 이상 떨어진 값
  • 모든 데이터가 정규 분포를 따르지 않을 수 있기 때문에 다음 상황에서는 제한됨
    - 데이터가 크게 비대칭일 때( → Log변환 등을 노려볼 수 있음)
    - 샘플 크기가 작을 경우

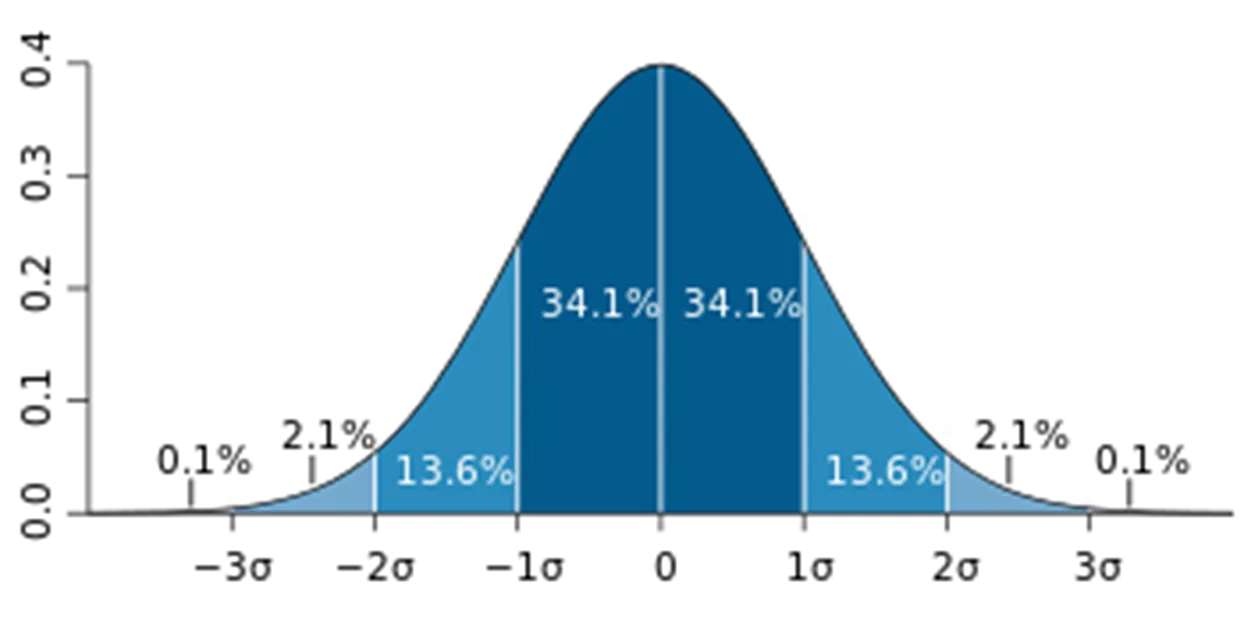
    2) IQR(Inter Quantile Range)를 이용한 이상치 발견
  • ESD와 동일하게 데이터가 비대칭적이거나 샘플사이즈가 작은 경우 제한됨
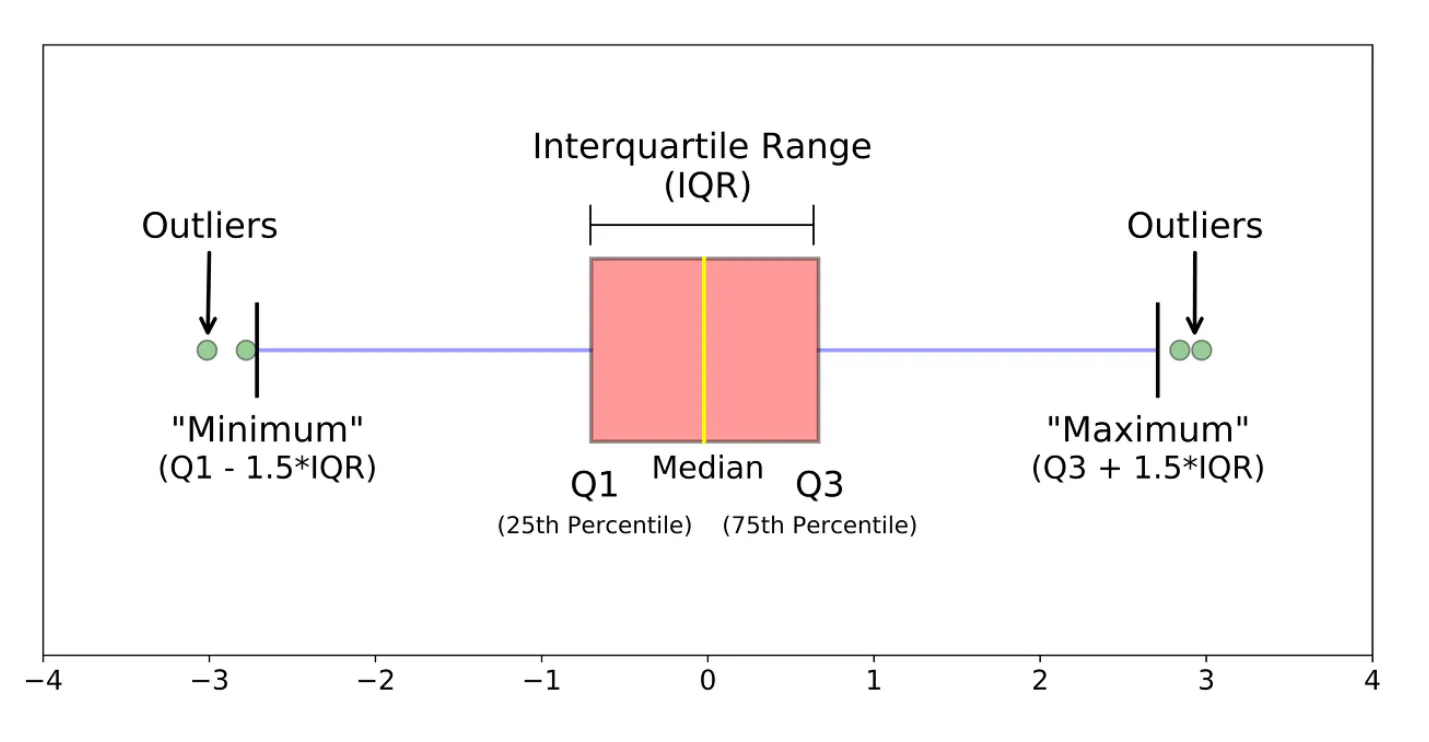
  • Box plot: 데이터의 사분위 수를 포함하여 분포를 보여주는 시각화 그래프, 상자-수염 그림이라고도 함
    - 사분위 수: 데이터를 순서에 따라 4등분 한 것
    Q1(25%),Q2(50%,중위수),Q3(75%)Q1(25\%), Q2(50\%,중위수), Q3(75\%)
    IQR(Inter quantile range)=Q3−Q1IQR(Inter \ quantile \ range) = Q3 - Q1
    상한 이상치=Q3+1.5∗IQR하한 이상치=Q1−1.5∗IQR상한 \ 이상치 = Q3 + 1.5*IQR \\ 하한 \ 이상치 = Q1 - 1.5*IQR
  • 이상치 발견 방법
    • ESD를 이용한 처리
import numpy as np
mean = np.mean(data)
std = np.std(data)
upper_limit = mean + 3*std
lower_limit = mean - 3*std

IQR을 이용한 처리(box plot)

Q1 = df['column'].quantile(0.25)
Q3 = df['column'].qunatile(0.75)
IQR = Q3 - Q1
uppper_limit = Q3 + 1.5*IQR
lower_limit = Q1 - 1.5*IQR

조건필터링을 통한 삭제(a.k.a. boolean Indexing): df[ df['column'] > limit_value]
📌이상치는 사실 주관적인 값. 그 데이터를 삭제 할지 말지는 분석가가 결정할 몫. 다만, 이상치는 도메인과 비즈니스 맥락에 따라 그 기준이 달라지며, 데이터 삭제 시 품질은 좋아 질 수 있지만 정보 손실을 동반하기 때문에 이상치 처리에 주의해야 한다. 단지, 통계적 기준에 따라서 결정 할 수도 있다는 점을 알아두기!

또한, 이상 탐지(Anomaly Detection)이라는 이름으로 데이터에서 패턴을 다르게 보이는 개체 또는 자료를 찾는 방법으로도 발전 할 수 있다. 예를 들면 사기탐지, 사이버 보안 등.
☑️ 결측치(Missing Value)
:결측치(Missing Value)는 존재하지 않는 데이터

  • 결측치 처리 방법
    • 수치형 데이터
      • 평균 값 대치: 대표적인 대치 방법
      • 중앙값 대치: 데이터에 이상치가 많아 평균 값이 대표성이 없다면 중앙 값을 이용
        Ex) 이상치는 평균 값을 흔들리게 함
  • 범주형 데이터
    • 최빈값 대치
  • 사용 함수
    • 간단한 삭제 & 대치
      • df.dropna(axis = 0): 행 삭제
      • df.dropna(axis = 1): 열 삭제
      • Boolean Indexing
      • df.fillna(value): 특정 값으로 대치(평균, 중앙, 최빈값)
# fillna 이용한 대치
age_mean = titaninc_df['Age'].mean().round(2)
titaninc_df['Age_mean'] = titaninc_df['Age'].fillna(age_mean)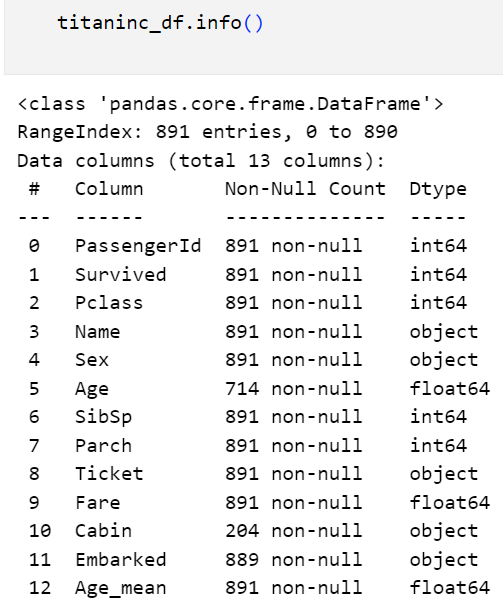

  • 알고리즘을 이용
    - sklearn.impute.SimpleImputer:평균, 중앙, 최빈값으로 대치
    - SimpleImputer.statistics_ : 대치한 값 확인 가능
    - sklearn.impute.IterativeImputer: 다변량대치(회귀 대치)
    - sklearn.impute.KNNImputer: KNN 알고리즘을 이용한 대치
    📌위와 같이 간단하게 결측치를 대치할 수도 있지만, 알고리즘을 이용해 대치할 수 도 있다. 이는 Imputation이라는 방법론으로 통계학에서도 많이 발전되었고, 석사 전공으로도 따로 있다.

예를 들면, 대표적인 알고리즘인 K- Nearest Neighbors(k 최근접 이웃)이라는 방법이 있다.

☑️ 범주형 데이터 전처리 - 인코딩(Encoding)
:인코딩의 사전적 뜻은 어떤 정보를 정해진 규칙에 따라 변환하는 것을 뜻. 반면, 우리가 만든 머신러닝 모델은 숫자를 기반으로 학습하기 때문에 반드시 인코딩 과정이 필요.
1) 레이블 인코딩(Label Encoding)
- 정의: 문자열 범주형 값을 고유한 숫자로 할당
- 1등급 → 0
- 2등급 → 1
- 3등급 → 2
- 특징
- 장점: 모델이 처리하기 쉬운 수치형으로 데이터 변환
- 단점: 실제로는 그렇지 않은데, 순서 간 크기에 의미가 부여되어 모델이 잘못 해석 할 수 있음
- 사용 함수
- sklearn.preprocessing.LabelEncoder
- 메소드
- fit: 데이터 학습
- transform: 정수형 데이터로 변환
- fit_transform: fit과 transform을 연결하여 한번에 실행
- inverse_transform : 인코딩된 데이터를 원래 문자열로 변환
- 속성
- classes_: 인코더가 학습한 클래스(범주)

- 성별(Sex)은 LabelEncoder
- 항구(Embarked) OneHotEncoder

from sklearn.preprocessing import LabelEncoder, OneHotEncoder
le = LabelEncoder()
oe = OneHotEncoder()

le.fit(titaninc_df[['Sex']])

le.classes_

array(['female', 'male'], dtype=object)

titaninc_df['Sex_le'] = le.transform(titaninc_df[['Sex']])

2) 원-핫 인코딩(One-Hot Encoding)
- 정의: 각 범주를 이진 형식으로 변환하는 기법
- 빨강 → [1,0,0]
- 파랑 → [0,1,0]
- 초록 → [0,0,1]
- 특징
- 장점: 각 범주가 독립적으로 표현되어, 순서가 중요도를 잘못 학습하는 것을 방지, 명목형 데이터에 권장
- 단점: 범주 개수가 많을 경우 차원이 크게 증가(차원의 저주) , 모델의 복잡도를 증가, 과적합 유발
- 사용 함수
- pd.get_dummies
- sklearn.preprocessing.OneHotEncoder
- 메소드(LabelEncoder와 동일)
- categories_: 인코더가 학습한 클래스(범주)
- get_feature_names_out(): 학습한 클래스 이름(리스트)

# CSR 데이터 데이터프레임으로 만들기
csr_df = pd.DataFrame(csr_data.toarray(), columns = oe.get_feature_names_out())
# 기존 데이터프레임에 붙이기(옆으로)
pd.DataFrame([titaninc_df,csr_df], axis = 1)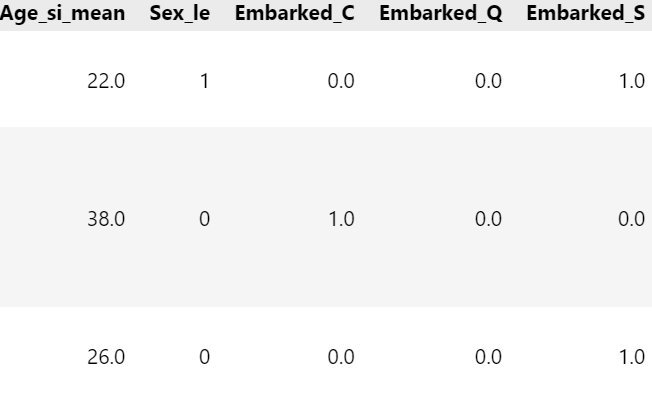

☑️ 수치형 데이터 전처리 - 스케일링(Scaling)
:인코딩이 범주형 자료에 대한 전처리라고 한다면, 스케일링은 수치형 자료에 대한 전처리
1) 표준화(Standardization)
- 각 데이터에 평균을 빼고 표준편차를 나누어 평균을 0 표준편차를 1로 조정하는 방법
- 수식

xnew=x−xmeanxstdx_{new} = \frac{x-x_{mean}}{x_{std}}
  • 함수: sklearn.preprocessing.StandardScaler
    - 메소드
    - fit : 데이터학습(평균과 표준편차를 계산)
    - transform: 데이터 스케일링 진행
    - 속성
    - mean_: 데이터의 평균 값
    - scale_, var_: 데이터의 표준 편차,분산 값
    - n_features_in_: fit 할 때 들어간 변수 개수
    - feature_names_in_: fit 할 때 들어간 변수 이름
    - n_samples_seen_ : fit 할 때 들어간 데이터의 개수
    - 특징
    - 장점
    - 이상치가 있거나 분포가 치우쳐져 있을 때 유용.
    - 모든 특성의 스케일을 동일하게 맞춤. 많은 알고리즘에서 좋은 성능
    - 단점
    - 데이터의 최소-최대 값이 정해지지 않음.
    2) 정규화(Normalization)
    - 정의: 데이터를 0과 1사이 값으로 조정(최소값 0, 최대값 1)
    - 수식
    xnorm=x−xminxmax−xminx_{norm} = \frac{x-x_{min}}{x_{max}-x_{min}}
  • 함수: sklearn.preprocessing.MinMaxScaler
    - (표준화와 공통인 것은 제외)
    - 속성
    - data_min_: 원 데이터의 최소 값
    - data_max_: 원 데이터의 최대 값
    - data_range_ : 원 데이터의 최대-최소 범위
    - 특징
    - 장점
    - 모든 특성의 스케일을 동일하게 맞춤
    - 최대-최소 범위가 명확
    - 단점:
    - 이상치에 영향을 많이 받을 수 있음(반대로 말하면 이상치가 없을 때 유용)
    3) 로버스트 스케일링(Robust Scaling)
    - 정의: 중앙값과 IQR을 사용하여 스케일링.
    - 수식
    xrobust=x−medianIQRx_{robust} = \frac{x-median}{IQR}
  • 특징
    - 장점: 이상치의 영향에 덜 민감
    - 단점: 표준화와 정규화에 비해 덜 사용됨
    • 함수: sklearn.preprocessing.RobustScaler
      • 속성
        • center_: 훈련 데이터의 중앙값
  1. 데이터 분리
    ☑️ 과적합은 머신러닝의 적
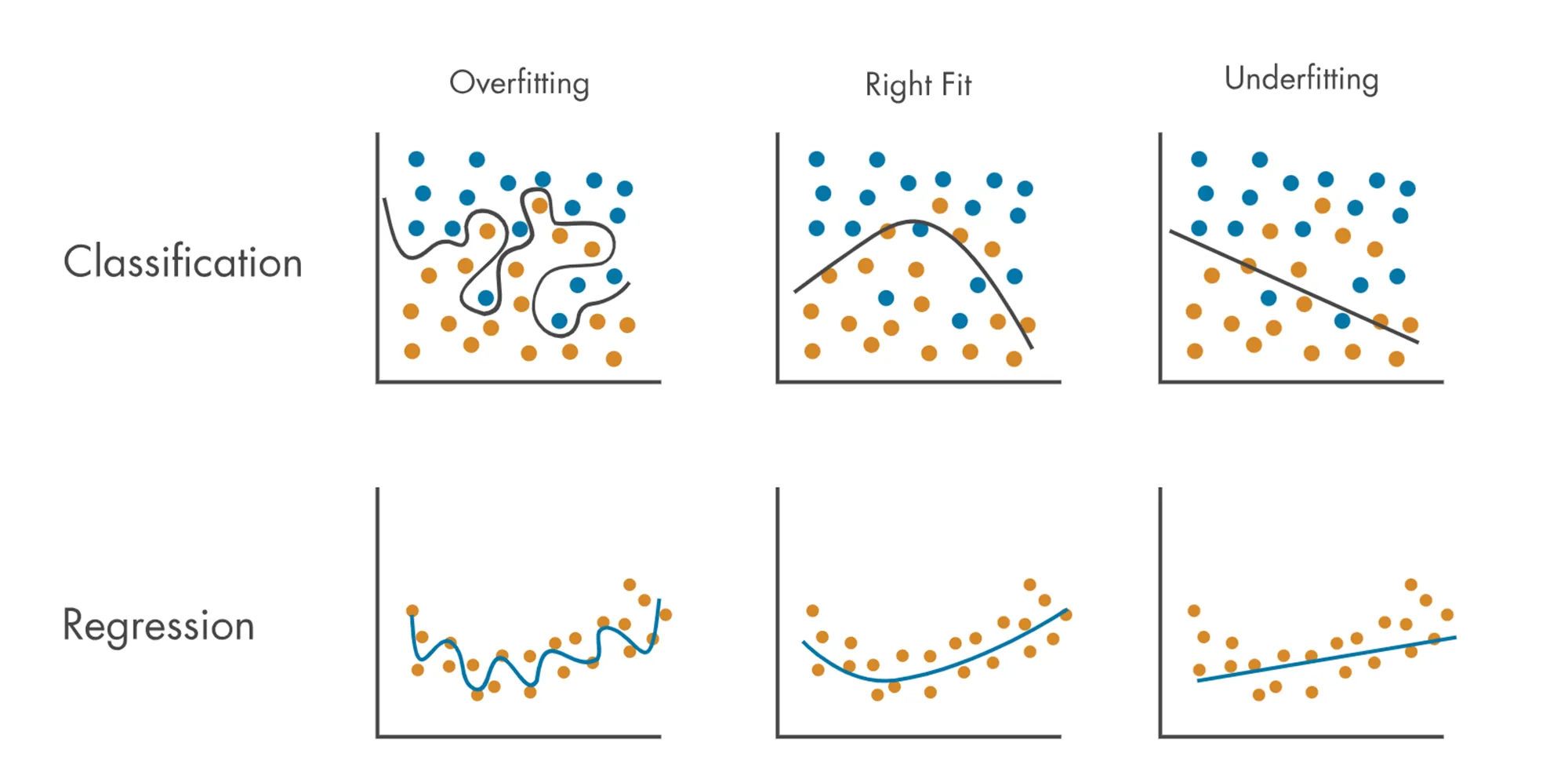
    :국소적인 문제를 해결하는 것에 집중한 나머지 일반적인 문제를 해결하지 못하는 현상을 과대적합 이슈라 한다. 즉, 과대적합(Overfitting)이란 데이터를 너무 과도하게 학습한 나머지 해당 문제만 잘 맞추고 새로운 데이터를 제대로 예측 혹은 분류하지 못하는 현상이다.

  • 예측 혹은 분류를 하기 위해서 모형을 복잡도를 설정

    • 모형이 지나치게 복잡할 때 : 과대 적합이 될 수 있음
    • 모형이 지나치게 단순할 때: 과소 적합이 될 수 있음

  • 과적합의 원인

    • 모델의 복잡도(상기의 예시)
    • 데이터 양이 충분하지 않음
    • 학습 반복이 많음(딥러닝의 경우)
    • 데이터 불균형(정상환자 - 암환자의 비율이 95: 5)
      ☑️ 과적합 해결 - 테스트 데이터의 분리
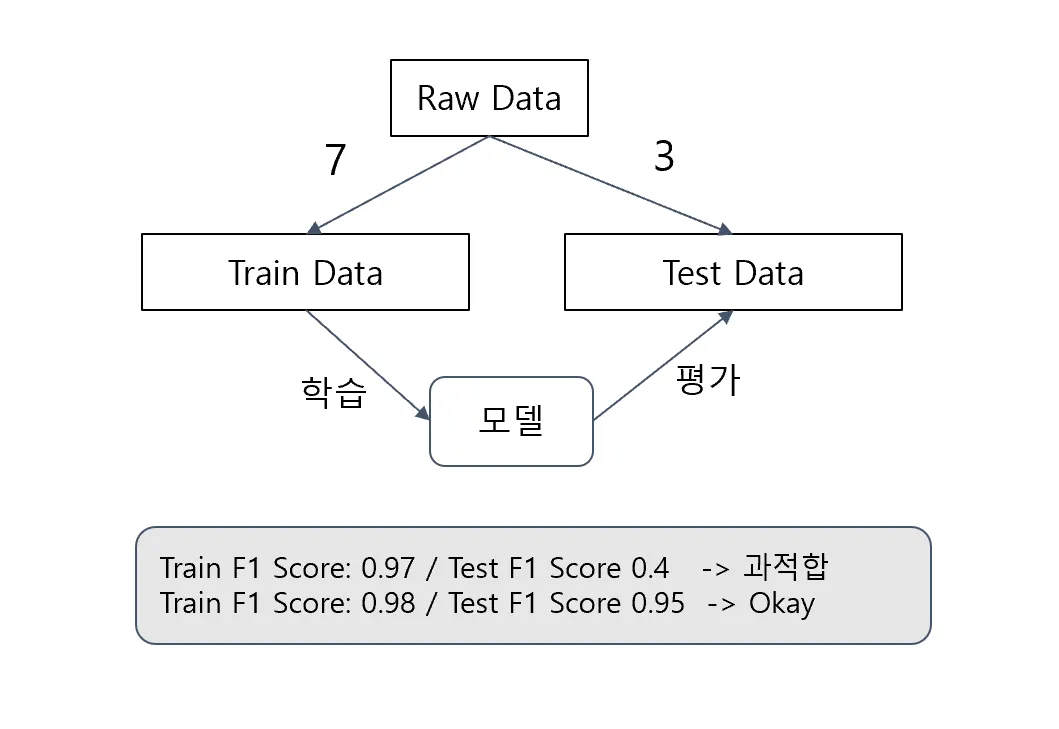      *train과 test의 수치가 크면안되고, 보통은 test가 조금 더 작게 나온다.

  • 학습 데이터(Train Data): 모델을 학습(fit)하기 위한 데이터

  • 테스트 데이터(Test Data): 모델을 평가 하기 위한 데이터

  • 함수 및 파라미터 설명

    • sklearn.model_selection.train_test_split
      • 파라미터
        • test_size: 테스트 데이터 세트 크기
        • train_size: 학습 데이터 세트 크기
        • shuffle: 데이터 분리 시 섞기
        • random_state: 호출할 때마다 동일한 학습/테스트 데이터를 생성하기 위한 난수 값. 수행할 때 마다 동일한 데이터 세트로 분리하기 위해 숫자를 고정 시켜야 함
      • 반환 값(순서 중요)
        • X_train, X_test, y_train, y_test

  • train_test_split

  • X변수: Fare, Sex

  • Y변수: Survived 

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(titaninc_df[['Fare','Sex']], titaninc_df[['Survived']],
                                                    test_size = 0.3, shuffle= True, random_state= 42,stratify=titaninc_df[['Survived']])
                                                    print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)

(623, 2) (268, 2) (623, 1) (268, 1)
y값의 분포가 일정하게 나오지 않을 경우를 대비하여 stratify= 이조건 붙여주기!

5.데이터 전체 프로세스적용 순서
1) 데이터 로드 & 분리
- train / test 데이터 분리

train_df = pd.read_csv("C:/Users/user/Documents/ML/titanic/train.csv")
test_df = pd.read_csv("C:/Users/user/Documents/ML/titanic/test.csv")

2) 탐색적 데이터 분석(EDA)
- 분포확인 & 이상치 확인

train_df.describe(include = 'all')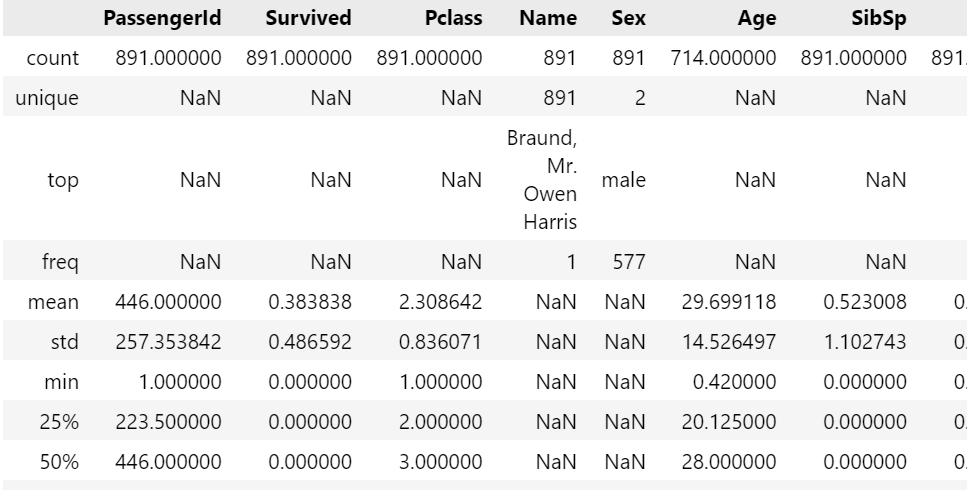

#기초가공: Family 변수생성
train_df_2 = train_df.copy()
def get_family(df):
    df['Family'] = df['SibSp'] + df['Parch'] + 1
    return df
get_family(train_df_2).head(3)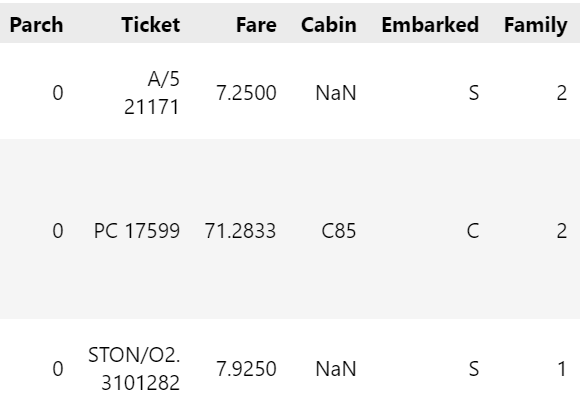

# 숫자형 변수들의 이상치를 확인하기 위하여 pairplot
sns.pairplot(train_df_2[['Age','Fare','Family']])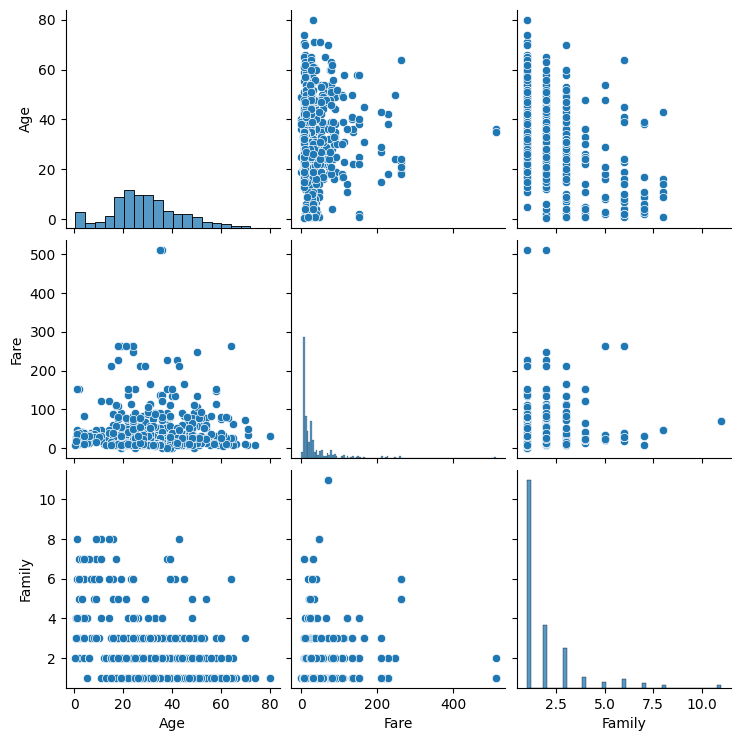

train_df_2 = train_df_2[train_df_2['Fare'] < 512]
train_df_2.shape

(888, 13)

train_df_2[['Fare']].describe()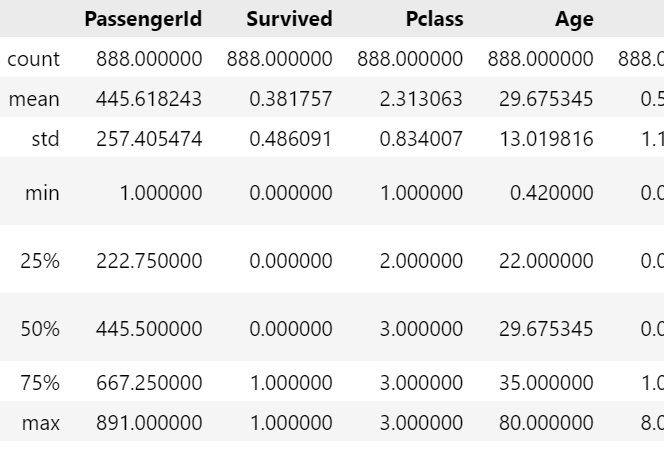

3) 데이터 전처리

  • 결측치 처리
    • 수치형: Age
    • 범주형: Embarked
    • 삭제 : Cabin, Name
  • 전처리
    • 수치형: Age, Fare, Sibsp+Parch
    • 범주형
      a> 레이블 인코딩: Pclass, Sex
      b> 원- 핫 인코딩: Embarked
# 결측치처리
def get_non_missing(df):
    Age_mean = train_df_2['Age'].mean()
    Fare_mean = train_df_2['Fare'].mean()
    df['Age'] = df['Age'].fillna(Age_mean)
    #train 데이터에는 필요하지않으나 test데이터에 결측치 존재해서 추가 
    df['Fare'] = df['Fare'].fillna(Fare_mean)
    df['Embarked'] = df['Embarked'].fillna('S')
    return df
get_non_missing(train_df_2).info()

def get_numeric_sc(df):
    # sd_sc: Fare , mm_sc : Age, Family
    from sklearn.preprocessing import StandardScaler, MinMaxScaler
    sd_sc = StandardScaler()
    mm_sc = MinMaxScaler()
    
    sd_sc.fit(train_df_2[['Fare']])
    df['Fare_sd_sc'] = sd_sc.transform(df[['Fare']])
    
    mm_sc.fit(train_df_2[['Age','Family']])
    df[['Age_mm_sc','Family_mm_sc']] = mm_sc.transform(df[['Age','Family']])
    
    return df
get_numeric_sc(train_df_2).describe()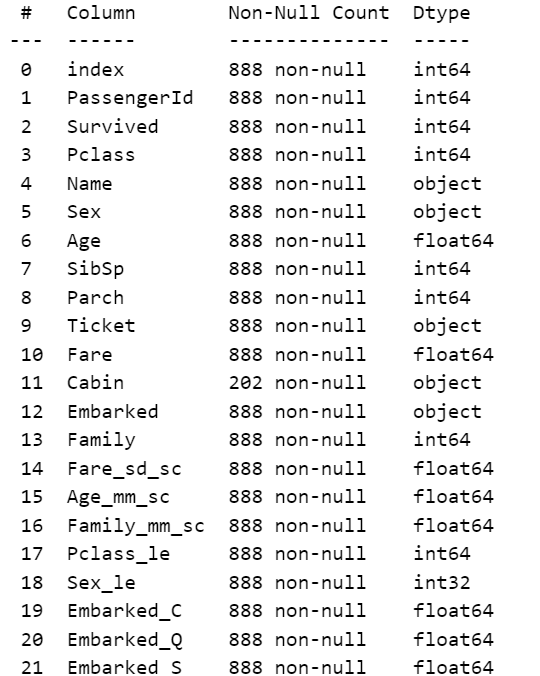

def get_category(df):
    
    from sklearn.preprocessing import LabelEncoder, OneHotEncoder
    le = LabelEncoder()
    le2 = LabelEncoder()
    oe = OneHotEncoder()
    
    le.fit(train_df_2[['Pclass']])
    df['Pclass_le'] = le.transform(df['Pclass'])
    
    le2.fit(train_df_2[['Sex']])
    df['Sex_le'] = le2.transform(df['Sex'])
    
    #index reset을 하기위한 구문
    df = df.reset_index()
    oe.fit(train_df_2[['Embarked']])
    embarked_csr = oe.transform(df[['Embarked']])
    embarked_csr_df = pd.DataFrame(embarked_csr.toarray(), columns = oe.get_feature_names_out())
    df = pd.concat([df, embarked_csr_df], axis = 1)
    return df

train_df_2 = get_category(train_df_2)
train_df_2.info()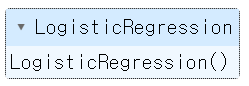

4) 모델 수립

def get_model(df):
    from sklearn.linear_model import LogisticRegression
    model_lor = LogisticRegression()
    X = df[['Age_mm_sc','Fare_sd_sc','Family_mm_sc','Pclass_le','Sex_le','Embarked_C','Embarked_C','Embarked_C']]
    y = df[['Survived']]
    return model_lor.fit(X,y)
    
model_output = get_model(train_df_2)
model_output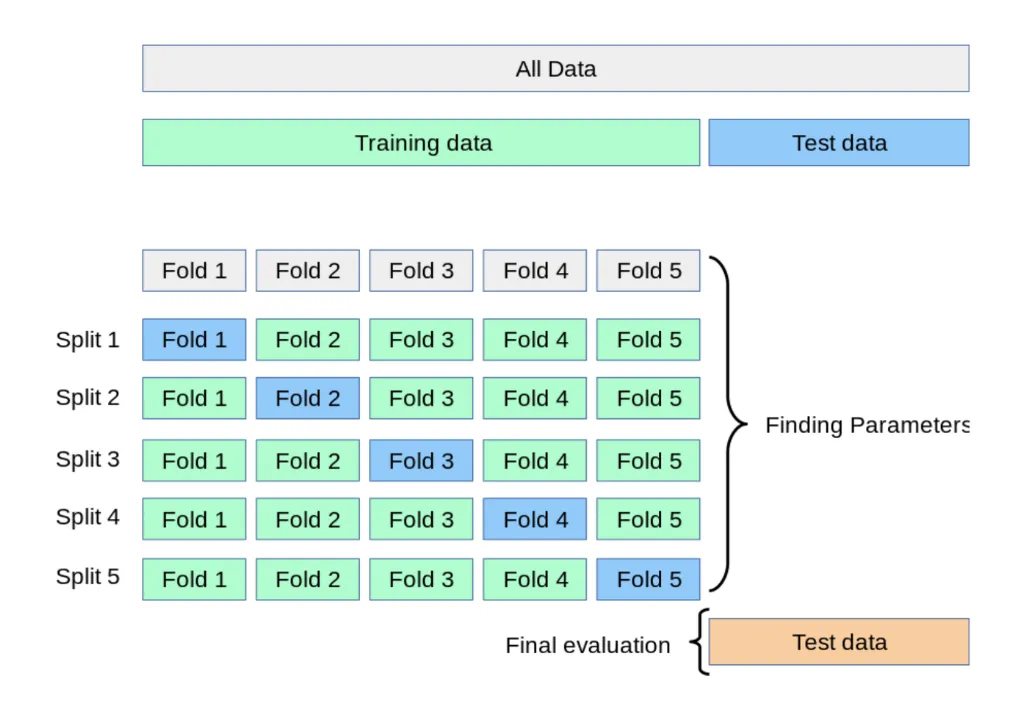

5) 평가

X = train_df_2[['Age_mm_sc','Fare_sd_sc','Family_mm_sc','Pclass_le','Sex_le','Embarked_C','Embarked_C','Embarked_C']]
y_pred = model_output.predict(X)

#평가
from sklearn.metrics import accuracy_score,f1_score
print(accuracy_score(train_df_2['Survived'],y_pred))
print(f1_score(train_df_2['Survived'],y_pred))

0.8029279279279279
0.7311827956989247

  1. 교차 검증과 GridSearch
    ☑️ 교차 검증(Cross Validation)
    ;모델을 평가하기 위한 별도의 테스트 데이터로 평가하는 과정을 알아보았다. 하지만 이때도, 고정된 테스트 데이터가 존재하기 때문에 과적합을 취약한 단점이 존재. 이를 피하기 위해서 교차검증방법 실시
    교차검증(Cross Validation)이란 데이터 셋을 여러 개의 하위 집합으로 나누어 돌아가면서 검증 데이터로 사용하는 방법.

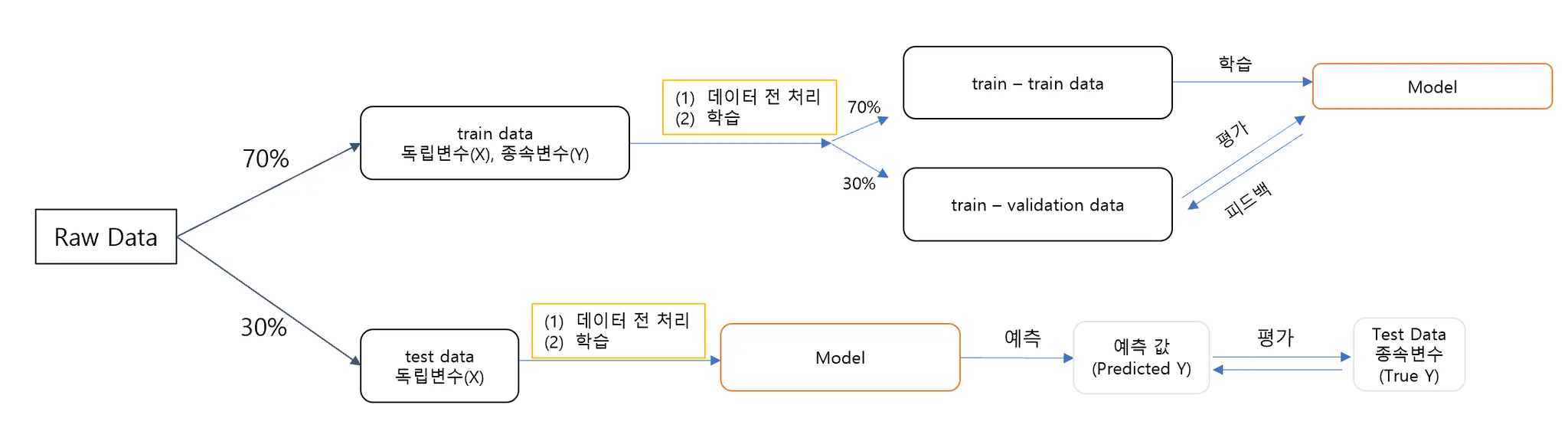
  • K-Fold Validation
    - 정의: Train Data를 K개의 하위 집합으로 나누어 모델을 학습시키고 모델을 최적화 하는 방법
    - 이때 K는 분할의 갯수
    - Split 1: 학습용(Fold 2~5), 검증용(Fold1)
    - Split 2: 학습용(Fold1, 3~5), 검증용(Fold2)
    - Split 5까지 반복 후 최종 평가

  • 특징

    • 데이터가 부족할 경우 유용합니다.(반복 학습)

  • 함수

    • skelarn.model_selection.KFold
    • sklearn.model_selection.StrifiedKFold: 불균형한 레이블(Y)를 가지고 있을 때 사용
from sklearn.model_selection import KFold
import numpy as np

kfold = KFold(n_splits = 5)
scores = []
X = train_df_2[['Age_mm_sc','Fare_sd_sc','Family_mm_sc','Pclass_le','Sex_le','Embarked_C','Embarked_C','Embarked_C']]
y = train_df_2['Survived']
for i, (train_index, test_index) in enumerate(kfold.split(X)):
    X_train, X_test = X.values[train_index], X.values[test_index]
    y_train, y_test = y.values[train_index], y.values[test_index]
    
    from sklearn.linear_model import LogisticRegression
    from sklearn.metrics import accuracy_score
    model_lor2 = LogisticRegression()
    model_lor2.fit(X_train,y_train)
    y_pred2 = model_lor2.predict(X_test)
    accuracy = accuracy_score(y_test, y_pred2).round(3)
    print(i,'번째 교차검증 정확도는', accuracy)
    scores.append(accuracy)

print('평균 정확도', np.mean(scores))

0 번째 교차검증 정확도는 0.787
1 번째 교차검증 정확도는 0.798
2 번째 교차검증 정확도는 0.775
3 번째 교차검증 정확도는 0.763
4 번째 교차검증 정확도는 0.831
평균 정확도 0.7908
☑️ 하이퍼 파라미터 자동적용하기 - GridSearchV
:모델을 구성하는 입력 값 중 사람이 임의적으로 바꿀 수 있는 입력 값이 있다. 이를 하이퍼 파라미터(Hyper Parameter)라고 한다. 다양한 값을 넣고 실험할 수 있기 때문에 이를 자동화해주는 Grid Search를 적용해볼 수 있다.

from sklearn.model_selection import GridSearchCV

params = {'solver' : ['newton-cg','lbfgs','liblinear','sag','saga'],
         'max_iter' : [100,200]}
grid_lor = GridSearchCV(model_lor2, param_grid = params, scoring='accuracy', cv = 5)
grid_lor.fit(X_train, y_train)

print('최고의 하이퍼 파라미터',grid_lor.best_params_)
print('최고의 정확도', grid_lor.best_score_.round(3))

from sklearn.model_selection import GridSearchCV

params = {'solver' : ['newton-cg','lbfgs','liblinear','sag','saga'],
'max_iter' : [100,200]}
grid_lor = GridSearchCV(model_lor2, param_grid = params, scoring='accuracy', cv = 5)
grid_lor.fit(X_train, y_train)

print('최고의 하이퍼 파라미터',gridlor.best_params)
print('최고의 정확도', gridlor.best_score.round(3))

key point

  • 데이터 분석 프로세스 정리

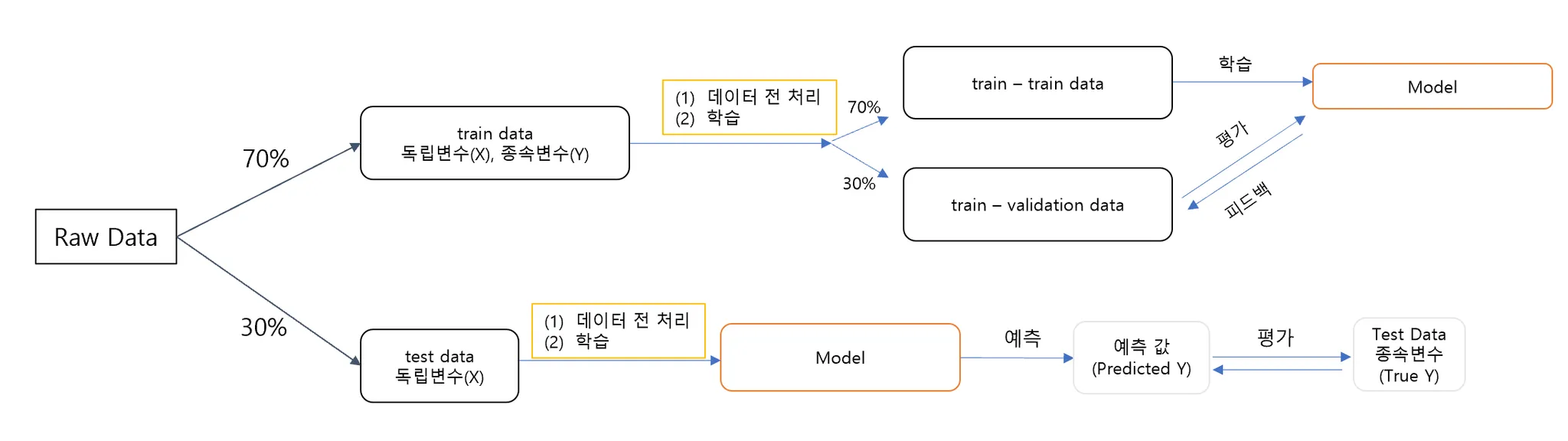
  1. Raw Data (원본 데이터)
    데이터가 처음 입력되면 전체 데이터를 두 부분으로 나눈다:
    Train Data (학습 데이터): 전체 데이터의 70%를 사용.
    Test Data (테스트 데이터): 나머지 30%를 사용.

  2. Train Data 처리 및 학습
    (1) 데이터 전처리: 학습 데이터의 독립변수(X)와 종속변수(Y)를 정리하고 필요한 전처리를 수행.
    (2) 학습: 전처리된 데이터를 기반으로 모델을 학습시킨다.
    학습 데이터(train data)는 다시 내부적으로 두 부분으로 나뉜다:
    Train-Train Data (70%): 모델 학습에 직접 사용.
    Train-Validation Data (30%): 모델의 성능을 검증(validation)하는 데 사용.
    이 단계에서 학습된 모델은 검증 데이터를 통해 성능 평가 및 피드백을 받는다.

  3. Test Data 처리 및 모델 예측
    Test Data 전처리 및 독립변수(X) 사용: 테스트 데이터도 학습 데이터처럼 전처리를 거침.
    학습된 모델을 사용하여 테스트 데이터의 X 값을 기반으로 종속변수 Y 값을 예측.

  4. 모델 평가
    모델이 생성한 예측값 (Predicted Y)와 테스트 데이터에 포함된 실제 True Y (테스트 데이터의 종속변수)를 비교하여 최종 성능을 평가.

📌모델의 일반화 능력을 확인하기 위해 데이터를 학습 데이터와 테스트 데이터로 분리하고, 모델 성능 평가 및 최적화를 위해 검증 데이터를 사용하는 것이 핵심!

profile
Arin lee
Be DBA
이전 포스트

[머신러닝]머신러닝의 이해와 라이브러리 활용 기초_분류분석 - 로지스틱회귀이론 및 실습

다음 포스트

[아티클 스터디]내 커리어도 피벗팅 할 수 있을까?

0개의 댓글