[통계학] 라이브 세션 4회차_01회귀분석

CONTENTS

• 회귀분석이란?
• 회귀분석의 특징, 종류
• 정합성 검증 & 결과 해석

SUMMARY

1. 회귀분석이란?
   👉 회귀분석 이해하기
   -게임시간과 전기세에 대한 데이터
   
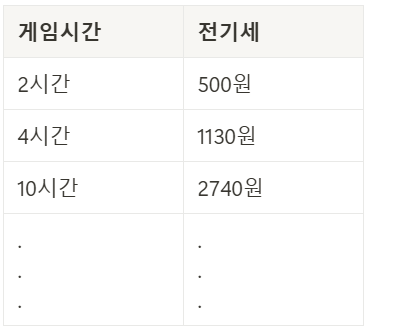
   -그래프의 x 축은 게임시간을, y 축은 전기세를 의미하고, 점들은 각 데이터를 의미
   → 독립변수는 원인이 되는 변수를 위미하며, 이는 곧 게임시간이 되게 됩니다.
   → 종속변수는 결과가 되는 변수를 위미하며, 이는 곧 전기세가 됩니다.
   
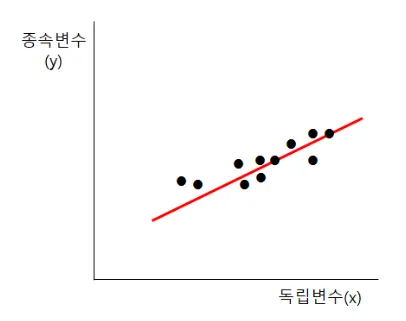
   -그렇다면 만약 게임시간이 1000시간이면, 전기세는 얼마일까요?
   *우리가 가진 데이터셋에 해당 값이 없을 때, 이를 예측하기 위해 ‘회귀분석’의 개념이 도입.
   이러한 예측을 위해 위 그래프에서 붉은색으로 보이는 ‘추세선’이 필요!
   회귀분석의 목적은 이 ‘추세선’을 찾는 것이 목적

추세선 = “우리가 이미 가지고 있는 데이터들을 가장 잘 설명해주는 선” 을 의미합니다.
추세선은  y = a+bx (방정식)으로 표현됩니다. 

x: 게임시간(독립변수)
y: 전기세(종속변수) 
a: 절편(x 가 0일때 y값)
b: 기울기 

이렇게 추세선을 파악함으로써, 게임시간이 1000시간과 추세선이 만나는 점을 통해 종속변수를
예측할 수 있게 되는 것. 이러한 특징을 통해, 데이터분석에서는 예측을 진행할 때 회귀분석을 주로 수행한다.

👉 회귀분석 요약

• 정의: 독립변수(x)로 종속변수(y)를 예측하는 분석기법
• 프로세스: 일반적으로 3단계를 통해 분석이 진행.
  1) 독립변수, 종속변수 설정
  독립변수와 종속변수를 정하고 가설을 설정.

→ 독립변수: 게임시간
→ 종속변수: 전기세
→ 귀무가설: 게임시간은 전기세와 관련이 없을 것이다.
→ 대립가설: 게임시간은 전기세와 관련이 있을 것이다.

2) 데이터 경향성 확인
독립변수와 종속변수 간 산점도 분석 및 상관관계 분석을 통해
데이터 분포를 확인.

3. 정합성 검증 & 결과 해석
   회귀분석 결과를 해석하기 위해 다음 3가지를 살펴본다.
   1️⃣ 회귀모델(회귀식)이 얼마나 설명력을 갖는지
   2️⃣ 회귀모델(회귀식)이 통계적으로 유의한지
   3️⃣ 독립변수와 종속변수 간 선형관계가 있는지

4. 회귀분석의 특징, 종류
   👉 특징

• 장점
  • 친밀성: 예측문제 해결에서 가장 많이 사용되고 있는 방법으로 분석 및 해석 방법이 다수 존재
  • 유용성: 결과에 대한 근어, 이유, 활용방안 등의 정보를 얻는 데 유용
  • 유연성: 종속변수를 설명하기 위한 다양한 독립변수를 선택하고 실험할 수 있음
• 단점
  • 복잡성: 기본 가정이 어긋나면 회귀분석을 사용할 수 없음
  • 한계성: 비선형성 확인을 위한 적절한 방식이 존재하지 않음

👉 종류
회귀분석은 회귀 계수의 선형여부, 독립변수의 개수, 종속변수의 개수에 따라 여러가지 유형으로 나눌 수 있다.

• 선형회귀분석
  
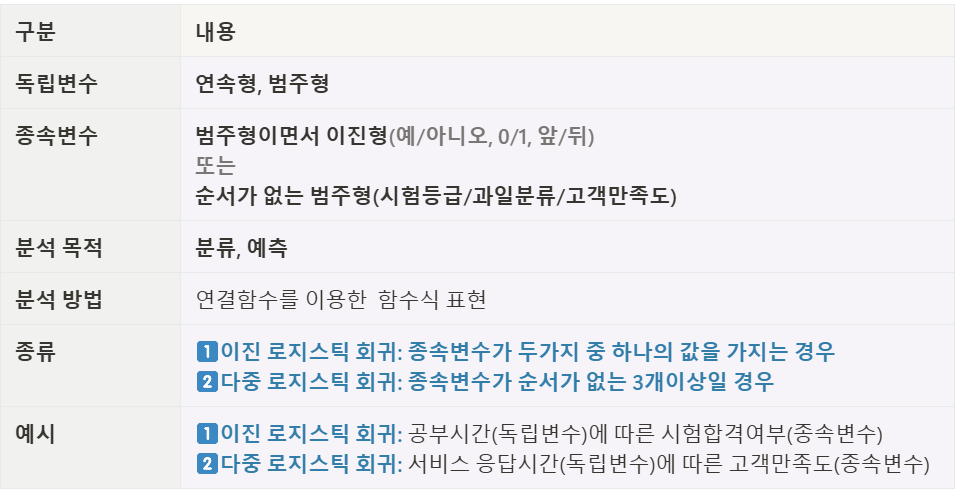
• 로지스틱 회귀분석
  

3. 정합성 검증 & 결과 해석
   1️⃣ 회귀모델(회귀식)이 얼마나 설명력을 갖는지? 
   → 결정계수 R_squared(R²) 를 확인.
   :결정계수는 종속변수와 독립변수의 관계를 나타내는 수치

• 회귀식 도출 과정
  
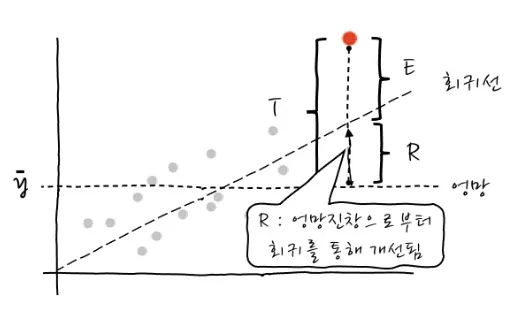
  -T,R,E 개념
  
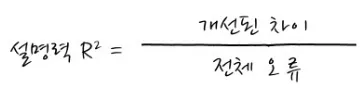
• 설명력(R²)은 전체오류중 회귀를 함으로써 얼마나 개선되었는가를 의미
• 설명력은 0과 1 사이의 값을 가지며, 1에 가까울수록 모델의 성능이 좋다는 것을 의미
  
  2️⃣ 회귀모델(회귀식)이 통계적으로 유의한지?
  → 회귀식에 대한 F검정 시행
  
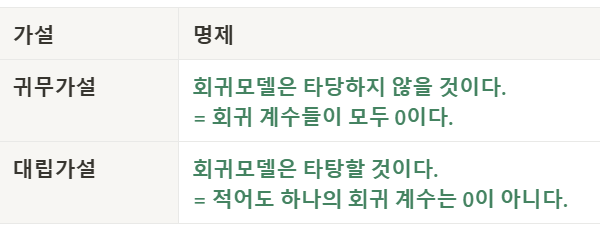
  → p-value로 유의성을 판단
  → F-검정을 통해 얻은 p-value 값이 0.05보다 작다면 대립가설을 채택. (신뢰도95%)
  3️⃣ 독립변수와 종속변수 간 선형관계가 있는지?
  → 회귀식의 $\beta_1$(기울기) 에 대한 t 검정 시행
  
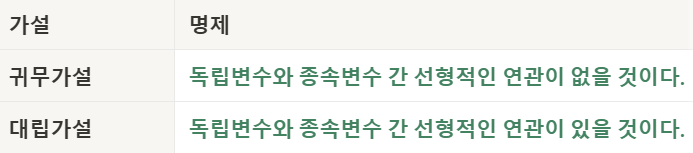
  → p-value로 유의성을 판단
  → t-검정을 통해 얻은 p-value 값이 0.05보다 작다면 대립가설을 채택
  4️⃣ OLS(Ordinary Least Squares) 해석하기
  OLS 는 선형 회귀 모델의 결과를 나타내는 회귀 결과 표. ols에서는 summary 라는 함수를 지원해주는데 summary를 통해 아래와 같은 결과표를 얻을 수 있다.
  
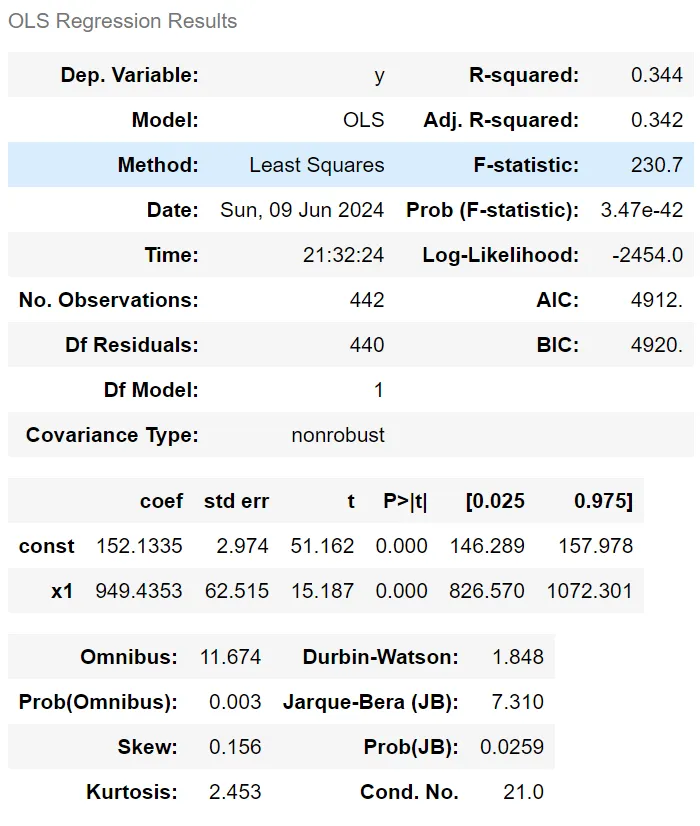
• 전체 해석
  📌Dep. Variable (y), R-squared (0.344), F-statistic (230.7),Prob (F-statistic) (3.47e-42), coef (coefficients), std err (Standard Error), t (t-statistic),P>|t| (P-value), [0.025 0.975] (Confidence Interval)
  1)Dep. Variable (y): 종속 변수, 즉 회귀분석에서 설명하고자 하는 변수.
  2)R-squared (0.344): 결정계수로, 회귀 모델이 종속 변수의 변동성을 얼마나 설명하는지를 나타낸다. 이 값은 0에서 1 사이에 위치하며, 0.344는 약 34.4%의 변동성이 설명된다는 것을 의미.
  3)Adj. R-squared (0.342): 수정된 결정계수로, 설명 변수의 개수를 고려하여 R-squared 값을 조정한 것. 변수의 수가 늘어날 때 발생하는 과적합을 방지하기 위해 사용. 0.342는 모델이 적절하게 조정되었음을 나타낸다.
  4)Method (Least Squares): 사용된 회귀 방법이 최소제곱법임을 나타낸다.
  a. 최소제곱법: 근사적으로 구하려는 해와 실제 해의 오차의 제곱의 합이 최소가 되는 해를 구하는 방법.
  5) F-statistic (230.7): 회귀 모형의 전체 유의성을 검정하는 F-통계량. 값이 클수록 모형이 유의미할 가능성이 높다.
  6) Prob (F-statistic) (3.47e-42): F-통계량의 p-값으로, 이 값이 매우 작으면 (예: 0.05 이하) 대립가설을 채택할 수 있다. 이 경우 p-값이 거의 0에 가까우므로, 회귀 모형이 통계적으로 유의미하다고 볼 수 있다.
  7) Log-Likelihood (-2454.0): 회귀 모형의 로그 우도(likelihood). 값이 클수록 모형이 데이터에 더 잘 맞는다는 것을 의미.
  8) No. Observations (442): 사용된 관측치(데이터 포인트)의 수.
  9) Df Residuals (440): 잔차의 자유도, 즉 전체 데이터 포인트 수에서 회귀 계수의 수를 뺀 값.
  10) Df Model (1): 모델에 포함된 설명 변수의 수.
  11) Covariance Type (nonrobust): 공분산 추정의 유형을 나타낸다. nonrobust는 기본 공분산 추정이 사용되었음을 의미.
  12) coef (coefficients):
  - const (152.1335): 상수항(절편)으로, 독립변수가 0일 때 종속 변수의 예측값.
  - x1 (949.4353): 설명 변수 x1의 회귀 계수로, 독립변수가 1 단위 증가할 때 종속 변수가 평균적으로 949.4353 단위 증가한다는 의미.
  13) **std err (Standard Error)**: 회귀 계수 추정치의 표준 오차. 상수항과 x1에 각각 2.974, 62.515가 있다.
  14) t (t-statistic): 회귀 계수가 0인지 검정하는 t-값. 절대값이 클수록 해당 계수가 유의미할 가능성이 높다. x1의 t-값은 15.187로 매우 크며 유의미함을 나타낸다.
  15) P>|t| (P-value): 각 계수에 대한 p-값. 일반적으로 0.05보다 작으면 해당 계수는 유의미하다고 판단. x1과 상수항의 p-값은 모두 0으로, 매우 유의미.
  16) [0.025 0.975] (Confidence Interval): 회귀 계수에 대한 95% 신뢰구간. 예를 들어, x1의 신뢰구간은 [826.570, 1072.301]로, 이 범위 내에서 실제 계수가 있을 가능성이 95%.
  17) Omnibus (11.674): 잔차의 정규성을 검정하는 Omnibus 검정 통계량. 값이 작을수록 잔차가 정규분포에 가깝다는 의미.
  18) Prob(Omnibus) (0.003): Omnibus 검정의 p-값. 0.05보다 작으므로 잔차가 정규분포에서 벗어날 가능성이 있다.
  19) Skew (0.156): 잔차의 왜도(skewness). 값이 0에 가까울수록 대칭적.
  20) Kurtosis (2.453): 잔차의 첨도(kurtosis). 3에 가까울수록 정규분포에 가깝다. 2.453은 정규분포보다 조금 더 평평함을 의미.
  21) Durbin-Watson (1.848): 잔차의 자기상관을 검정하는 통계량. 2에 가까우면 자기상관이 없음을 의미.
  22) Jarque-Bera (JB) (7.310): 잔차의 정규성을 검정하는 Jarque-Bera 검정 통계량.
  23) Prob(JB) (0.0259): Jarque-Bera 검정의 p-값. 0.05보다 작아 잔차가 정규성을 만족하지 않을 가능성이 있다.
  24) Cond. No. (21.0): 설명 변수의 다중공선성을 나타내는 조건수. 값이 높으면 다중공선성 문제가 있음을 시사.

KEY POINTS

• 회귀분석 진행 단계

1. 독립변수, 종속변수 설정
2. 데이터 경향성 확인
3. 정합성 검증 & 결과 해석

• 회귀분석의 결과 해석을 위해 필요한 검증.
  • 회귀식이 얼마나 설명력을 가지는지
  • 회귀식이 통계적으로 유의한지
  • 독립변수와 종속변수 간 상관관계가 유의미한지
• 각각의 검정통계량(t-value, F-value)이 가지는 숫자의 의미보다, 이를 신뢰할 수 있는지(p-value)에 포커스 맞추기!

insight

• 파이썬으로 로지스틱 회귀분석을 구현할 때와 머신러닝 관점에서 중요한 점!

1. 데이터 준비와 전처리
   결측치 처리: 결측치는 로지스틱 회귀의 성능을 저하시킬 수 있다. 이를 평균, 중간값으로 채우거나 제거해야 한다.
   특성 스케일링: 많은 머신러닝 알고리즘이 그렇듯, 로지스틱 회귀도 스케일이 큰 특성에 의해 영향을 받을 수 있으므로, 데이터를 표준화(Standardization)나 정규화(Normalization)해야 한다.
   카테고리 데이터 인코딩: 범주형 변수를 One-Hot Encoding 또는 Label Encoding으로 변환하여 모델이 처리할 수 있도록 한다.

---

2. 피처 선택
   다중공선성 검사: 다중공선성은 두 특성이 높은 상관관계를 가지는 경우를 의미하며, 모델 성능과 해석력을 저하시킬 수 있다. VIF(분산 팽창 인자) 분석으로 이를 감지하고 해결할 수 있다.
   유의미한 변수 선택: 데이터의 특성을 이해하고, 모델에 기여도가 낮거나 해를 끼칠 수 있는 변수는 제거.

---

3. 모델 학습
   훈련 및 검증 데이터 분리: 데이터를 훈련 세트와 검증 세트로 나눠야 과적합(Overfitting)을 방지하고 모델 성능을 정확히 평가할 수 있다.
   정규화(Regularization): L1(라쏘) 또는 L2(릿지) 정규화를 통해 모델의 과적합을 방지할 수 있습니다. 파이썬에서는 LogisticRegression 클래스에서 penalty 파라미터로 설정 가능합니다.

---

4. 성능 평가
   적절한 지표 선택: 로지스틱 회귀는 주로 이진 분류 문제에 사용되므로 정확도 외에 F1-score, Precision, Recall, AUC-ROC와 같은 지표를 사용해 모델을 평가.
   혼동 행렬(Confusion Matrix): 예측 결과의 분포를 확인하여 모델의 오분류 유형을 분석.

---

5. 머신러닝 관점에서 추가 고려사항
6. 선형성 가정: 로지스틱 회귀는 특성과 로그 오즈(log-odds) 사이에 선형 관계를 가정. 이를 확인하기 위해 특성 변환(예: 로그, 다항식)을 사용할 수 있다.
7. 특성 상호작용: 특성 간 상호작용을 고려하면 모델이 더 좋은 성능을 발휘할 수 있다.
8. 확률 출력: 로지스틱 회귀는 클래스 소속 가능성을 제공하므로, 이를 활용해 최적의 임계값(Threshold)을 조정할 수 있다.
9. 확장성: 데이터가 크거나 차원이 높아지면 계산 비용이 증가할 수 있으므로, 샘플링 기법이나 고차원 데이터를 위한 대안을 고려.

파이썬 구현 예시

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report, confusion_matrix
# 1. 데이터 준비
X, y = ...  # 특성과 라벨 데이터 준비
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 2. 데이터 스케일링
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# 3. 로지스틱 회귀 모델 생성
model = LogisticRegression(penalty='l2', solver='liblinear')  # L2 정규화
model.fit(X_train, y_train)
# 4. 예측 및 평가
y_pred = model.predict(X_test)
print(confusion_matrix(y_test, y_pred))
print(classification_report(y_test, y_pred))

• 결론
  로지스틱 회귀는 간단하고 해석 가능한 모델이지만, 데이터 전처리, 특성 선택, 정규화, 성능 평가 등 여러 요소에 따라 성능이 좌우된다. 머신러닝 관점에서는 선형 가정의 한계와 과적합 방지 방법, 대규모 데이터에서의 효율성을 항상 염두에 두어야 한다.