[머신러닝]머신러닝의 이해와 라이브러리 활용 기초_선형회귀심화

contents

• 선형회귀 심화
• 선형회귀 정리

summary

1. 선형회귀 심화

• 다중선형회귀
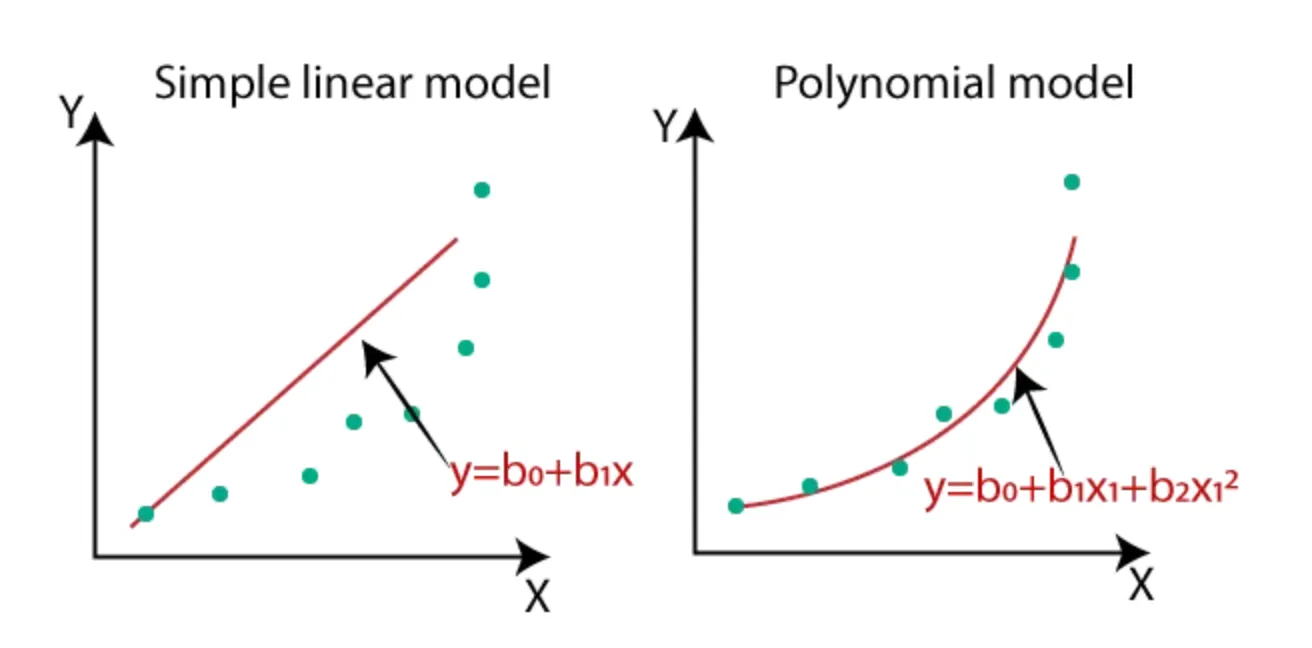
  -단순선형회귀 vs 다항회귀
  
• 범주형 데이터 사용하기
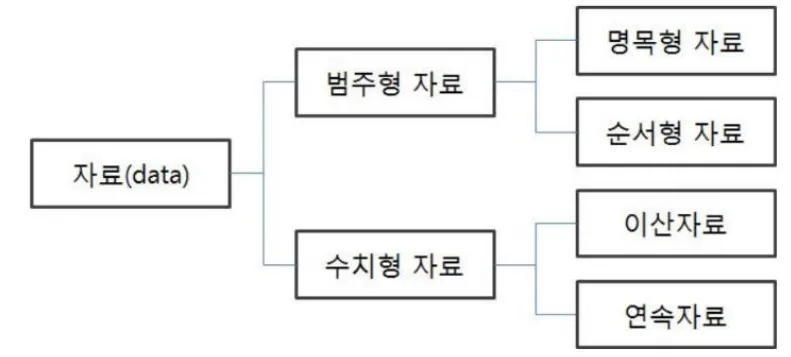
  ☑️ 수치형 데이터 vs 범주형 데이터
  
• 수치형 데이터

  1. 연속형 데이터: 두 개의 값이 무한한 개수로 나누어진 데이터

     ex) 키, 몸무게

  2. 이산형 데이터: 두 개의 값이 유한한 개수로 나누어진 데이터

     ex) 주사위 눈, 나이

• 범주형 데이터
  1. 순서형 자료: 자료의 순서 의미가 있음

      ex) 학점,등급
      
  2. 명목형 자료: 자료의 순서 의미가 없음
      
      ex) 혈액형, 성별

  ☑️ 범주형 데이터 실습
  앞서 팁에 대한 선형회귀 모델을 그려봤지만, 성능이 별로 좋지 않았고, 이제 이를 활용해 성별데이터를 사용하려고 한다.

-머신러닝 모델에 데이터를 훈련시킬려면 해당 데이터를 숫자로 바꿔야함
-성별, 날짜 와 같은 데이터를 범주형 데이터라고 부르며 이를 임의로 0,1 등에 숫자로 바꿀 수 있음. 이를 Encoding 과정이라 함

1) 범주형 데이터 인코딩
2) 훈련
3) 학습
4) 평가

tips_df.head(3)

# Female 0, Male 1
def get_sex(x):
    if x == 'Female':
        return 0
    else:
        return 1
        
#apply함수는 매 행을 특정한 함수 적용
tips_df['sex_en']=tips_df['sex'].apply(get_sex)
tips_df.head(3)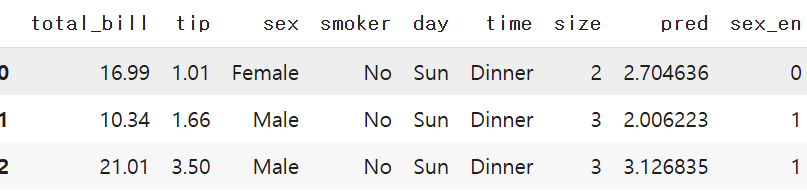

#모델 설계도 가져오기
model_lr3 = LinearRegression()
x = tips_df[['total_bill','sex_en']]
y = tips_df['tip']
x.head(3)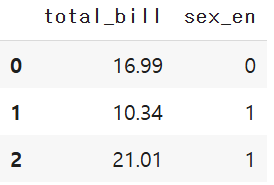

#학습
model_lr3.fit(x,y)

#예측
y_pred_tip2 = model_lr3.predict(x)
y_pred_tip2[:3]

array([2.72117624, 1.99477235, 3.1176016 ])

#단순선형회귀 mse: x변수가 전체 금액
#다중선형회귀 mes: x변수가 전체 금액, 성별
print('단순선형회귀', mean_squared_error(y_true_tip, y_pred_tip))
print('다중선형회귀', mean_squared_error(y_true_tip, y_pred_tip2))

단순선형회귀 1.036019442011377
다중선형회귀 1.0358604137213614

print('단순선형회귀', r2_score(y_true_tip, y_pred_tip))
print('다중선형회귀', r2_score(y_true_tip, y_pred_tip2))

단순선형회귀 0.45661658635167657
다중선형회귀 0.45669999534149974

• 설명
  위를 보면 아주 미세하게 성능이 좋아진것을 볼 수 있으나 거의 차이가 없으므로 성능이 나아졌다고 말할 수 없다. 이유는 데이터를 자세히 확인하지 않았고, 전처리가 없었으며, 데이터의 수가 적다

#원래는 밑에 그래프를 그려보면서 전체 데이터가 얼마나 차이가 있는지 확인하는 과정이 필요했다.
sns.barplot(x='sex', y='tip', data=tips_df)
plt.title('Sex & Tip')
plt.xlabel('Sex')
plt.ylabel('Tip')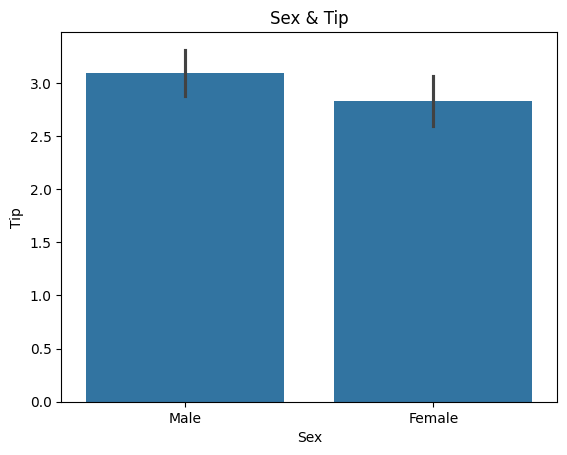

2. 선형회귀 정리
   ☑️ 선형 회귀의 가정
   📌머신러닝모델 중에 선형회귀는 이해하기 쉽고 방법도 쉬운 장점이 있지만 말 그대로 X-Y변수간의 선형적 관계가 좋아야만 좋은 성능을 낸다.
   1)선형성 (Linearity): 종속 변수(Y)와 독립 변수(X) 간에 선형 관계가 존재해야 함
   
   2)등분산성 (Homoscedasticity): 오차의 분산이 모든 수준의 독립 변수에 대해 일정해야 합니다. 즉, 오차가 특정 패턴을 보여서는 안 되며, 독립 변수의 값에 상관없이 일정해야 합니다.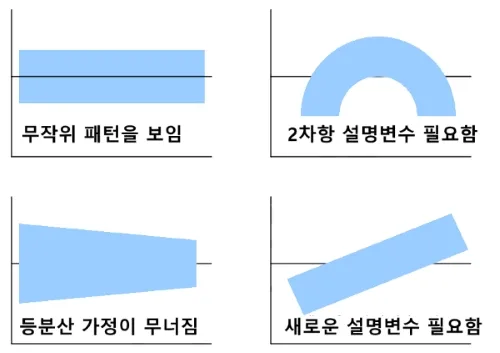
   3)정규성 (Normality): 오차 항은 정규 분포를 따라야 합니다.
   
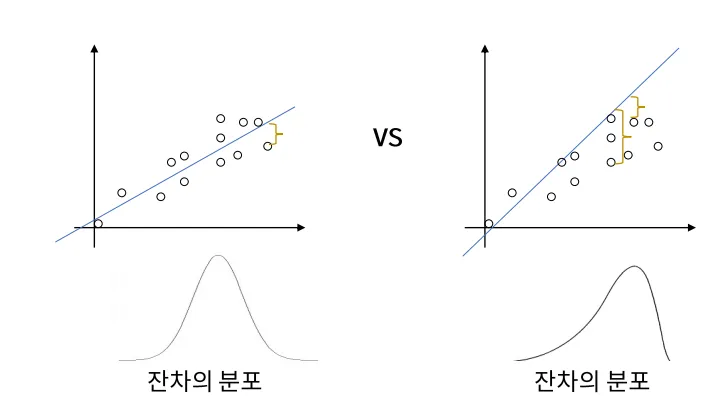
   4)독립성 (Independence): X변수는 서로 독립적이어야 합니다.

• 다중공선성 문제
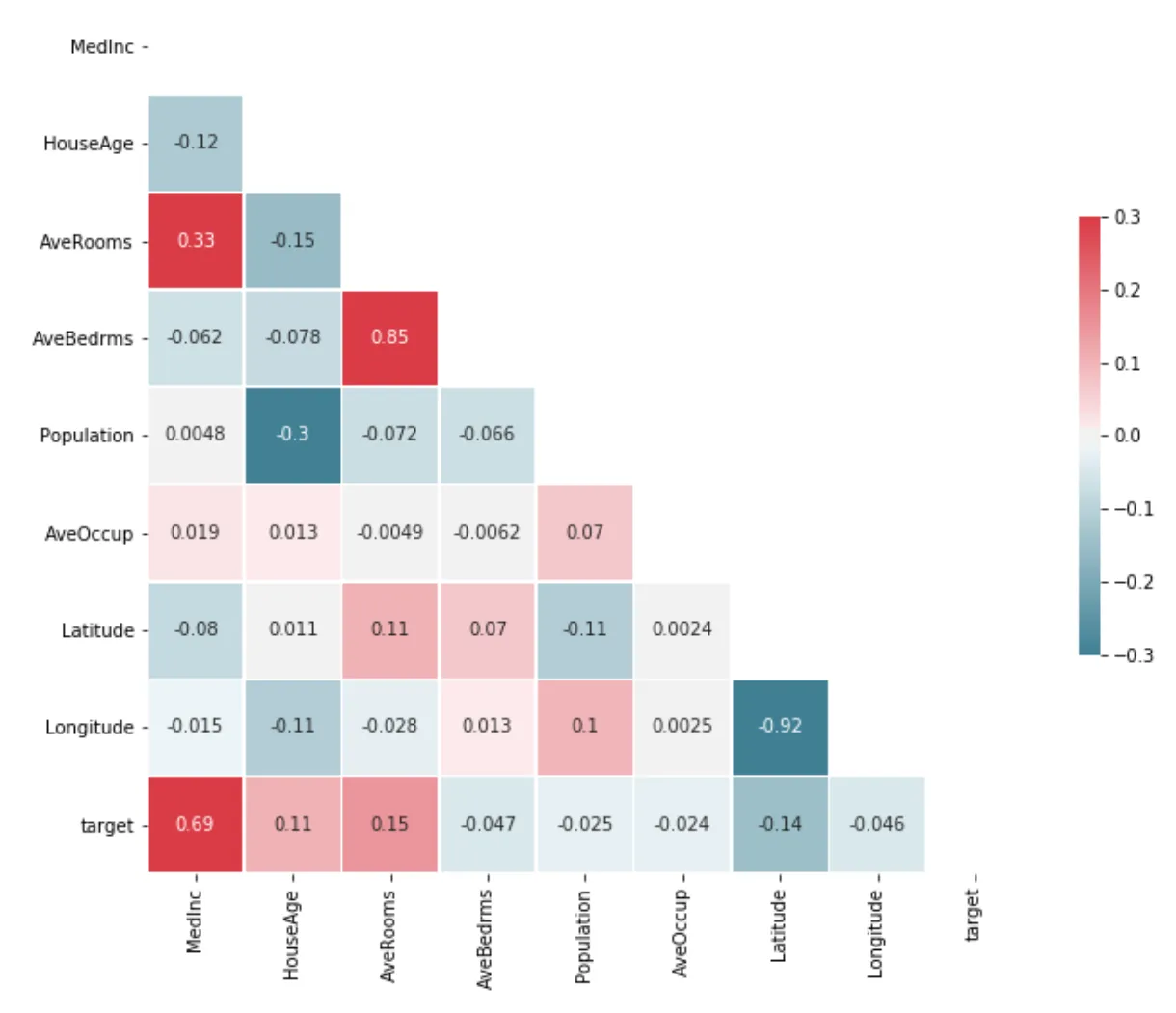
  📌변수가 많아지면 서로 연관이 있는 경우가 많다. 이처럼 회귀분석에서 독립변수(X)간의 강한 상관관계가 나타나는 것을 다중공선성(Multicolinearity)문제라고 함.

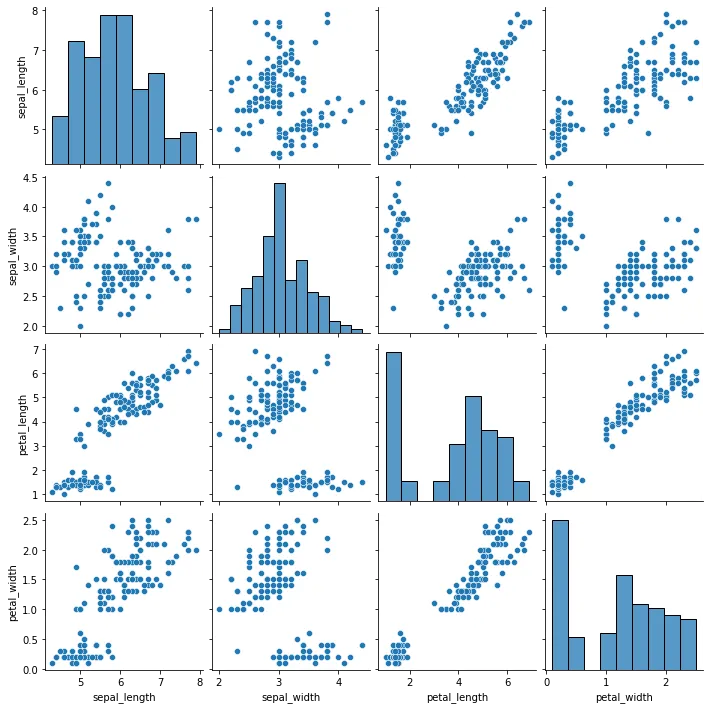
만약 위에서 예시를 들었던 Weight, Height 가지고 다른 Y(이를 테면 발사이즈)를 예측한다면 Weight, Height가 연관있는 변수이기 때문에 다중공선성 문제가 나타난다.
-Weight vs Height 산점도

• 다중공선성 해결방법
  - 서로 상관관계가 높은 변수 중 하나만 선택(산점도 혹은 상관관계 행렬)
  - 두 변수를 동시에 설명하는 차원축소(Principle Component Analysis, PCA) 실행하여 변수 1개로 축소
  
  
  
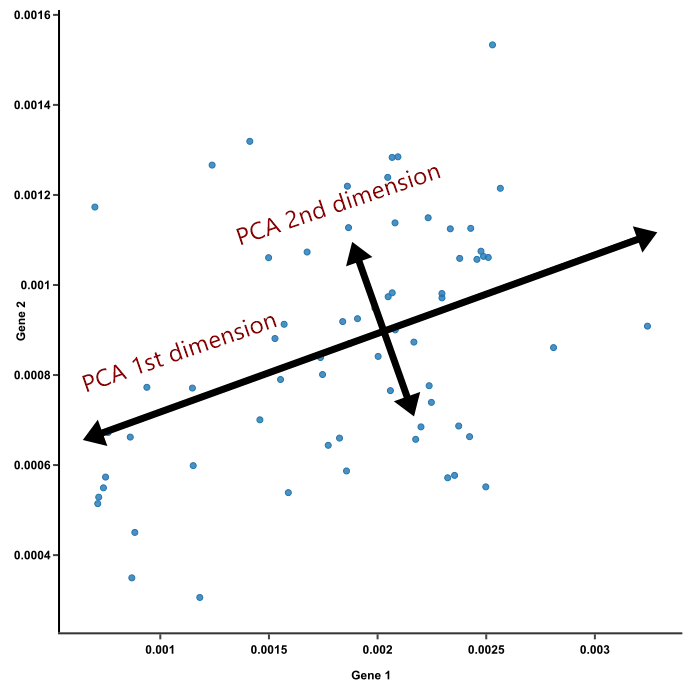
  ☑️ 선형 회귀정리
• 장점
  • 직관적이며 이해하기 쉽다. X-Y관계를 정량화 할 수 있다.
  • 모델이 빠르게 학습된다(가중치 계산이 빠르다)
• 단점
  • X-Y간의 선형성 가정이 필요하다.
  • 평가지표가 평균(mean)포함 하기에 이상치에 민감하다.
  • 범주형 변수를 인코딩시 정보 손실이 일어난다.
• Python 패키지
  • sklearn.linear_model.LinearRegression

insight

선형회귀의 경우 선형관계가 없다면 유의미한 결과를 얻기에 다소 무리가 있다. 사실 우리 주변의 데이터는 뚜렸한 직선의 형태를 보이지 않는 경우가 다수이기에 실제 데이터에 선형회귀 모델을 적용하는 것은 무리가 있지 않을까 하는 생각이든다.
하지만, 기본적인 지식이고, 이로인해 다른 모델을 이해하기에 훨씬 용이하기에 개념과 과정에 대해 잘 알아두는 것은 필수적으로 보인다.