[통계학] 라이브 세션 2회차(가설설정, 통계적 유의성, 가설검정 )

contents

• 데이터 분석가의 통계적 실험
• A/B TEST
• 유의수준 설정하기
• 검정통계량과 p-value

summary

1. 데이터 분석가의 통계적 실험
   
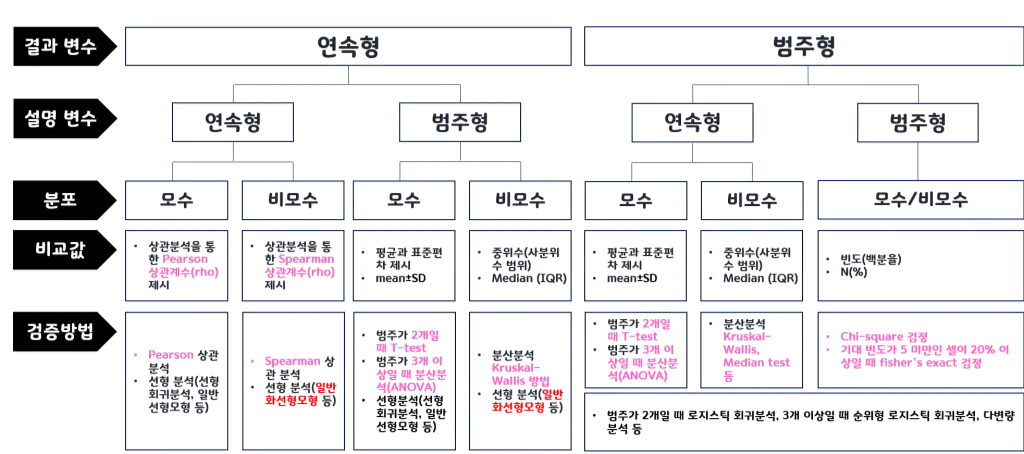
   *분홍색 표시의 분석을 중점으로!

• 모수통계: 모집단이 정규분포를 따른다는 가정하에 사용. 데이터분석가는 주로 모수통계를 진행. ****평균, 분산 등의 값을 알고 있다는 가정 하에 진행하는 통계분석.
• 비모수통계: 모집단이 정규분포가 아닐 때 사용. (이 말은 곧 표본의 크기가 충분히 크지 않음: 소규모 실험에 해당). 또는 평균, 분산 등의 값을 가정하지 않고 진행하는 통계분석.

2. A/B TEST (버킷테스트 또는 분할 테스트)
   : 마케팅 고객데이터 분석 중 가장 널리 사용되는 방법으로 A/B TEST 는 두 가지 처리 방법 중 어떠한 쪽이 더 좋다라는 것을 입증하기 위해 실험군을 두 그룹으로 나누어 진행하는 실험이다.
   종종 두 가지 처리 방법 중 하나는 기준이 되는 기존 방법이거나 아예 아무러 처리도 적용하지 않는 방법이 된다.

• 테스트의 목적은 1️⃣고객의 니즈파악 2️⃣최소 투자로 최대 이익을 창출하고자(ROI상승)
  ( UI/UX 개선,전환율 증가, 매출 증가)
  

• 🚩 주요 지표
  • 서비스 가입률
  • 재방문율
  • CTR(노출 대비 클릭률), CVR(클릭 대비 전환율, 구매전환율)
  • ROAS(캠페인 비용 대비 캠페인 수익)
  • eCPM(1,000회 광고 노출당 얻은 수익)

👉 프로세스
1)현행 데이터 탐색:주요 지표를 기준으로 현재 데이터 탐색
2)가설 설정:비즈니스 목표를 달성하는 데 필요한 KPI를 정의, KPI 전환율을 증가를 위한 귀무가설, 대립가설을 설정.
3)유의수준 설정: 귀무가설이 맞을 때 오류를 얼마나 허용할 것인지 기준을 정하는 단계
4)테스트 설계 및 실행: 사용자를 대조군과 실험군의 두 그룹으로 분리, 대조군 그룹에게는 제품이나 서비스의 현재 버전을 보여주고, 실험군 그룹에게는 새 버전을 노출 처리
5)테스트 결과 분석: 측정 항목(가설)에 대해 두 그룹의 결과를 분석합니다. (검정통계량 분석), 통계적 방법으로 결과를 분석하여 대조군과 실험군 사이의 통계적으로 유의미한 차이가 있는지 확인.

👉 A/B 테스트 주의사항

• 적절한 표본 크기
• 하나의 변수만 변경: 두 가지 이상의 변수를 동시에 변경하면 어떤 변수가 영향을 미쳤는지 파악할 수 없다.
• 무작위성
• 적절한 분석 방법
• 테스트 결과의 의미
• 정해진 기간 동안 진행
  

3. 유의수준 설정하기(α); 신뢰수준의 반대 개념
   : 표본을 추출하는 순간 모집단과 100% 일치할 수 없기 때문에, 오류의 가능성이 존재-> 가설 검정에서 결론을 해석하기 위해서는 기준을 세우고, 그 기준을 만족하는지 확인필요.
   여기서 기준이 되는 것이 유의수준이다.
   즉, 귀무가설(차이가 없을 것이라고 생각하는 가설)이 맞을 때 기각할 확률

• 신뢰도와의 관계
  :95%의 신뢰도를 기준으로 한다면 (1−0.95)인 0.05값이 유의수준이다.
  즉, 반대의 개념이라고 할 수 있다.
  
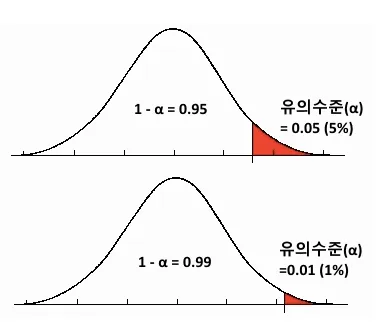
  🤩*파이썬을 통한 분석에서는 유의수준을 정하고 시작! 유의수준을 정하면 신뢰도가 자동으로 정해지기 때문!

4. 검정통계량과 p-value
   👉 결과 해석 단계 1: 검정 방식 정하기 & 검정통계량 계산하기

• 검정통계량: 귀무가설을 채택 또는 기각하기 위해 사용하는 확률 변수를 의미
  *확률변수: 특정 확률로 발생하는 각각의 결과를 수치값으로 표현하는 변수
  → 즉 확률에 대한 수치이므로, 0과 1 사이의 값을 가지게 된다.

[예제]
주사위를 던졌을 때 나오는 숫자를 확률변수 X 라고 가정했을 때,
각 X 에 대한 확률 P(X) 를 구하시오.

→ 확률변수 X는 1,2,3,4,5,6.
→ 주사위 값이 1~6 중 어떤 수가 나올지 모르기 때문에 우리는 이를 확률변수라고 한다.
→ 각 X 에 대한 확률은 1/6 이다.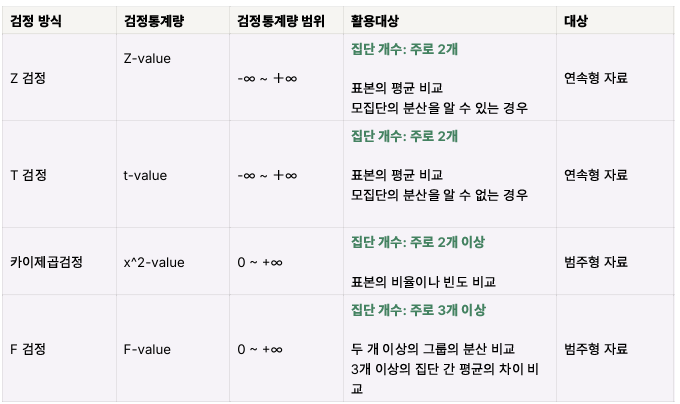

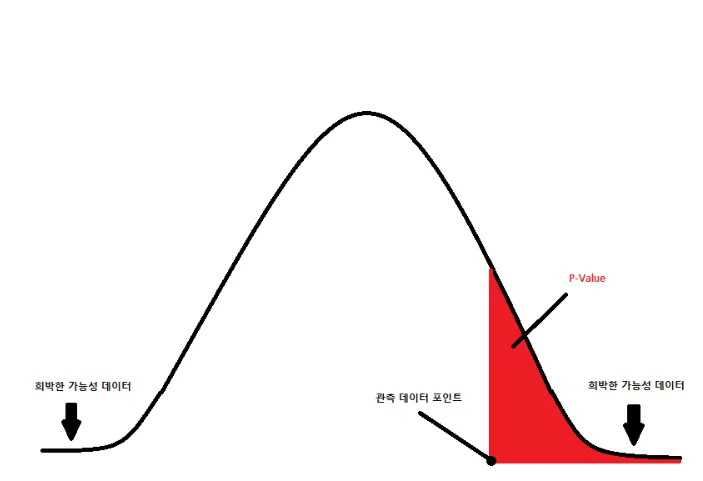
👉 결과 해석 단계 2: p-value(Probability-value )
:어떠 사건이 우연히 발생할 확률(0 이상이고 1 이하의 값)

• p-value가 0.05 보다 작다 = 우연히 일어났을 가능성이 거의 없다 = 인과관계가 있다고 추정
  = 대립가설 채택
• p-value가 0.05 보다 크다 = 우연히 일어났을 가능성이 높다 = 인과관계가 없다고 추정
  = 대립가설 기각

*우리가 원하는건 당연히 대립가설 채택!

key points

• 데이터분석가는 데이터 종류에 따라 알맞은 분석기법을 활용
• A/B 테스트라는 방법론을 통해 해당 과정에서 사용되는 통계개념(가설설정, 통계적 의미 해석, 가설검정)
• A/B 테스트 5가지 단계: 현행데이터탐색 → 가설설정 → 유의수준설정 → 실험 → 해석
• 귀무가설과 대립가설의 의미
  • 귀무가설은 차이가 없거나 의미 있는 차이가 없는 경우의 가설.
  • 대립가설은 차이가 있는 경우의 가설.
• 유의수준은 신뢰도의 반대 개념
  • 오류의 허용 범위=일반적으로 0.05를 사용.
  • 이는 곧 신뢰도 95% 를 의미.
• p-value 는 어떠한 사건이 우연하게 발생할 확률.
  • p-value가 0.05 보다 작다 = 우연히 일어났을 가능성이 거의 없다 = 인과관계가 있다고 추정
    = 대립가설 채택

insight

실습과정이 어려운것은 아니나, 개념에 대한 명확한 이해가 없으면, 다음단계로 넘어 갈 수 없으니, 반드시 위 내용을 숙지하기!

• 파이썬라이브러리 활용해 검정 통계량 계산하기(혼자서 해보기)

먼저, 데이터 준비하기

import pandas as pd
import numpy as np

# 데이터 로드
data = pd.read_csv('./statistics.csv')
data

1. Pandas describe():
   pandas.DataFrame.describe() 함수는 주요 통계량 (평균, 표준편차, 최소값, 사분위수 등)을 요약하여 제공하므로 빠른 데이터 탐색에 유용하다

# 주요 통계량 출력
print(data.describe())

   Customer ID          Age  Purchase Amount (USD)  Review Rating  \

count 3900.000000 3900.000000 3900.000000 3900.000000
mean 1950.500000 44.068462 59.764359 3.749949
std 1125.977353 15.207589 23.685392 0.716223
min 1.000000 18.000000 20.000000 2.500000
25% 975.750000 31.000000 39.000000 3.100000
50% 1950.500000 44.000000 60.000000 3.700000
75% 2925.250000 57.000000 81.000000 4.400000
max 3900.000000 70.000000 100.000000 5.000000

   Previous Purchases  

count 3900.000000
mean 25.351538
std 14.447125
min 1.000000
25% 13.000000
50% 25.000000
75% 38.000000
max 50.000000

2. Pingouin의 describe 함수:->ttest
   pingouin.describe()를 통해 각 열에 대한 통계 요약을 확인할 수 있다. -> 더이상 이용불가 하므로 ttest진행!

#설치
!pip install pingouin

import pingouin as pg

# 두 그룹의 데이터
group1 = [1, 2, 3, 4, 5]
group2 = [2, 3, 4, 5, 6]

# t-test 수행
ttest_result = pg.ttest(group1, group2)
print(ttest_result)

T-Test 수행
:Scipy와 Statsmodels의 t-test 및 ANOVA: 특정 검정 통계량을 원할 경우 scipy.stats.ttest_ind나 statsmodels의 ANOVA 등으로 개별 검정을 수행할 수 있다

1. t-값구하기(모집단의 분산을 모를때)

import pandas as pd
import numpy as np
from scipy import stats

# 데이터 불러오기
data = pd.read_csv('./statistics.csv')

# 무작위로 데이터 섞기
shuffled_data = data.sample(frac=1, random_state=1).reset_index(drop=True)

# 두 그룹으로 나누기
group1, group2 = np.array_split(shuffled_data, 2)

# 특정 수치형 열 선택 
t_stat, p_value = stats.ttest_ind(group1['Age'], group2['Age'])

print(f"Group 1:\n{group1}")
print(f"Group 2:\n{group2}")
print(f"T-Statistic: {t_stat}")
print(f"p-value: {p_value}")

T-Statistic: 0.6032905494009037
p-value: 0.546350519414948

• 결과 해석
  T-Statistic: 0.6032905494009037 , p-value: 0.546350519414948
  T-Statistic (T-통계량): 0.6033 t-통계량은 두 그룹의 평균 차이를 표준 오차로 나눈 값. 이 값이 절대값 기준으로 클수록 두 그룹 평균의 차이가 통계적으로 유의미할 가능성이 커진다. 0.6033은 비교적 작은 값으로, 두 그룹 간 평균 차이가 크지 않다는 것을 나타낸다.

p-value (p-값): 0.5464 p-값은 귀무가설이 참이라는 가정 하에 현재 관찰된 결과를 얻을 확률을 나타낸다. p-값이 0.5464로, 일반적인 유의수준인 0.05보다 훨씬 크다. 따라서 귀무가설을 기각하지 못한다.

"두 그룹의 평균 나이에 통계적으로 유의미한 차이가 없다"는 귀무가설을 유지. 즉, 두 그룹 간 평균 나이의 차이는 우연에 의한 차이일 가능성이 높다.
p-값이 0.5464라는 것은, 데이터가 두 그룹 간의 평균 차이에 대한 유의미한 증거를 제공하지 않는다는 것을 나타내며, 평균 나이에 유의미한 차이가 없다고 볼 수 있다. 결론적으로, 이 검정 결과는 두 그룹 간의 평균 나이 차이가 없다고 판단하기에 충분한 통계적 근거가 없다.

2. z-검정(모집단의 분산을 알때)

import numpy as np

# 데이터 불러오기
data = pd.read_csv('./statistics.csv')
data_age = data['Age']

# 표본 분산 계산
variance = np.var(data_age, ddof=1)  # ddof=1은 자유도를 조정하여 표본 분산 계산
print(f"표본 분산: {variance}")

표본 분산: 231.27076706058753

import numpy as np
from scipy import stats

# 무작위로 데이터 섞기
shuffled_data = data.sample(frac=1, random_state=1).reset_index(drop=True)

# 두 그룹으로 나누기
group1, group2 = np.array_split(shuffled_data, 2)

# 두 그룹의 데이터 
mean1 = group1['Age'].mean()
mean2 = group2['Age'].mean()
n1 = len(group1)
n2 = len(group2)

# 모집단의 분산 
sigma_squared = 231.27076706058753  #모집단의 분산
sigma = np.sqrt(sigma_squared)

# 표준 오차 계산
se = np.sqrt(sigma_squared / n1 + sigma_squared / n2)

# Z-통계량 계산
z_stat = (mean1 - mean2) / se

# p-value (양측 검정)
p_value = 2 * (1 - stats.norm.cdf(abs(z_stat)))

print(f"Z-Statistic: {z_stat}")
print(f"p-value: {p_value}")

Z-Statistic: 0.6033397625560087
p-value: 0.5462826861149823

• z-검정 해석하기
  Z-Statistic
  (Z-통계량): 0.6033 Z-통계량은 두 그룹의 평균 차이를 표준 오차로 나눈 값. 이 값이 클수록 (양수든 음수든 절대값 기준) 두 그룹 간의 평균 차이가 통계적으로 유의미할 가능성이 커진다. 그러나 0.6033은 상당히 작은 값으로, 두 그룹 간 평균 차이가 크지 않다는 것을 의미.
  p-value (p-값): 0.5463 p-값은 귀무가설이 참이라는 가정 하에 현재 관측된 결과를 얻을 확률. p-값이 일반적인 유의수준인 0.05보다 훨씬 큼. p-값이 0.5463이라는 것은, 두 그룹의 평균에 차이가 없다는 귀무가설을 기각하기에는 충분한 증거가 없다는 것을 나타냄.

결론
귀무가설 유지: 이 결과에 따르면, 두 그룹의 평균 나이에 통계적으로 유의미한 차이가 없다고 볼 수 있다. 즉, 두 그룹의 평균 차이는 우연에 의한 것일 가능성이 높다. p-값이 0.5463으로 크기 때문에, 두 그룹의 평균 나이가 동일하다는 가설을 기각할 근거가 부족. 따라서, "두 그룹의 나이 평균이 차이가 없다"는 귀무가설을 유지하는 것이 적절하며, 이 차이는 통계적으로 유의미하지 않다는 결론을 내릴 수 있다.

카이제곱검정(범주형 변수일 경우!)

import pandas as pd
import numpy as np
from scipy.stats import chi2_contingency

# 데이터 불러오기
data = pd.read_csv('./statistics.csv')

# 무작위로 데이터 섞기
shuffled_data = data.sample(frac=1, random_state=1).reset_index(drop=True)

# 두 그룹으로 나누기
group1, group2 = np.array_split(shuffled_data, 2)

# 각 그룹의 성별 빈도수 계산
group1_gender_counts = group1['Gender'].value_counts()
group2_gender_counts = group2['Gender'].value_counts()

# 두 그룹을 병합하여 카이제곱 검정에 사용할 분할표 생성
contingency_table = pd.DataFrame([group1_gender_counts, group2_gender_counts]).fillna(0)

# 카이제곱 검정 실행
chi2_stat, p_value, dof, expected = chi2_contingency(contingency_table)

print("Contingency Table (Observed):")
print(contingency_table)
print(f"Chi2 Statistic: {chi2_stat}")
print(f"p-value: {p_value}")
print(f"Degrees of Freedom: {dof}")
print("Expected Frequencies Table:")
print(expected)

Contingency Table (Observed):
Gender Male Female
count 1339 611
count 1313 637
Chi2 Statistic: 0.7364724736048265
p-value: 0.3907932190689667
Degrees of Freedom: 1
Expected Frequencies Table:
[[1326. 624.][1326. 624.]]

• 검정 결과 요약
  Observed Contingency Table (관측 분할표): 두 그룹에서 남성과 여성의 수는 다음과 같다: 그룹 1: 남성 1339명, 여성 611명 그룹 2: 남성 1313명, 여성 637명 Chi2 Statistic (카이제곱 통계량): 0.7365

카이제곱 통계량은 관측된 값과 기대값의 차이를 반영. 값이 클수록 그룹 간 차이가 클 가능성이 큼.

p-value (p-값): 0.3908 p-값은 관측된 결과가 귀무가설 하에서 발생할 확률을 나타냄. 일반적으로 p-값이 0.05보다 작으면 귀무가설을 기각. 여기서는 0.3908로, 귀무가설을 기각할 수 없다.

Degrees of Freedom (자유도): 1 카이제곱 검정에서 자유도는 두 그룹 간 독립성을 비교할 때 변수의 제약을 나타냄.

Expected Frequencies Table (기대 빈도표): 기대값은 각 그룹에서 성별 빈도가 귀무가설(성별 비율이 동일함)에 따라 계산된 값: 남성 기대값: 1326 여성 기대값: 624 관측된 값과 기대값의 차이를 기반으로 검정이 이루어진다.

해석 귀무가설: "두 그룹의 성별 분포는 차이가 없다." p-값 (0.3908)이 0.05보다 크기 때문에, 귀무가설을 기각할 수 없다. 즉, 두 그룹의 성별 분포 차이는 통계적으로 유의미하지 않다고 판단. 카이제곱 통계량 (0.7365)도 낮은 값으로, 두 그룹 간의 관측된 차이가 작고, 통계적으로 유의미하지 않은 차이를 나타냄.

결론 두 그룹의 성별 분포에 차이가 없다는 귀무가설을 유지할 수 있다. 즉, 통계적으로 유의미한 차이가 없다고 볼 수 있다. 성별에 있어서 두 그룹 간의 차이는 우연에 의한 것일 가능성이 높다.