Recap : Deep Graph Encoders
- GNN이 어떻게 노드 임베딩을 만드는지?
- 그래프 데이터 → GNN layer → 활성화 함수 → 정규화 → GNN layer → 출력 임베딩
- GNN은 노드와 엣지로 구성된 그래프를 입력 받아, 각 노드의 벡터 표현을 생성하는 신경망 구조
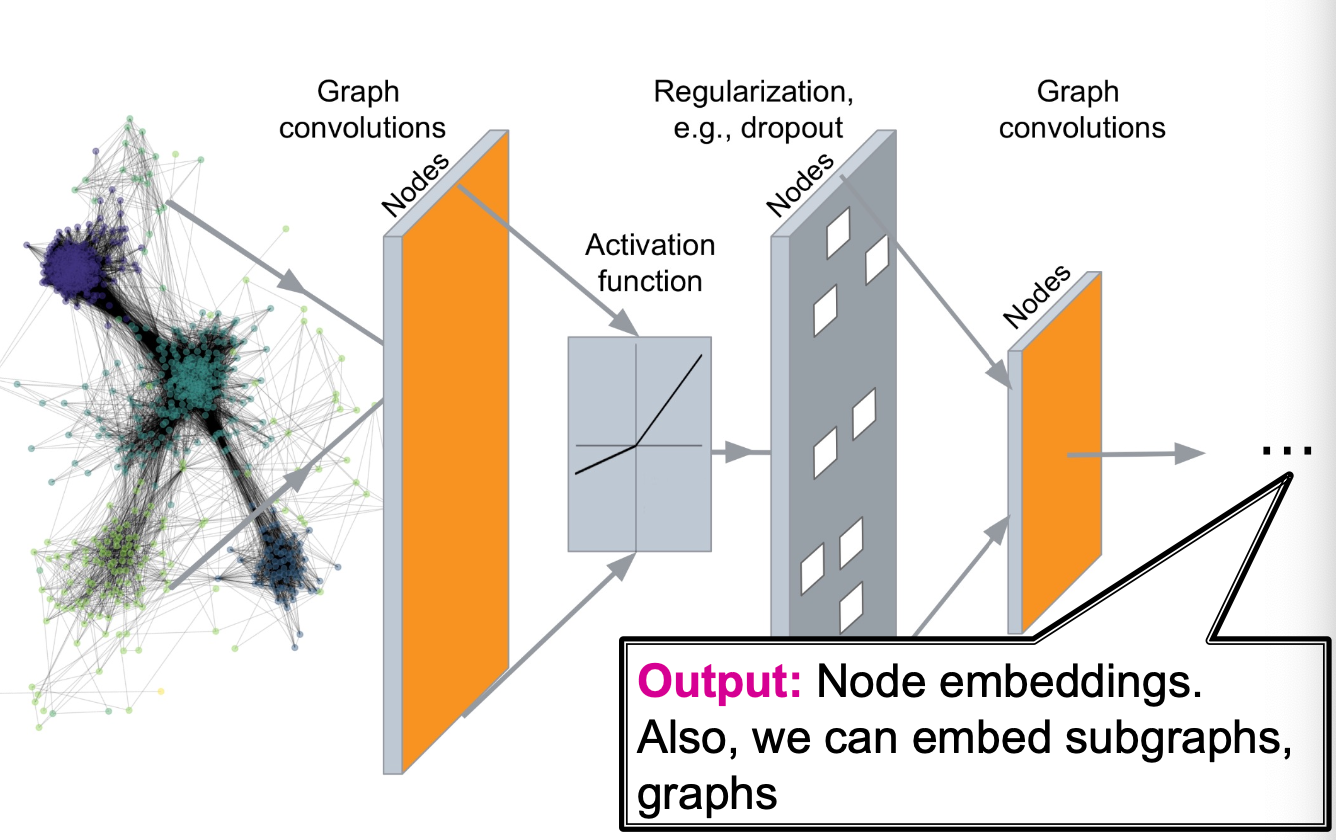
Recap : Graph Neural Networks
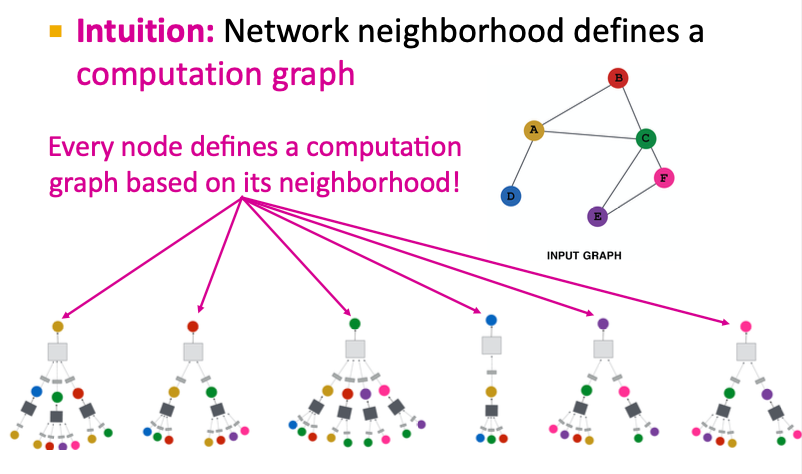
각 노드의 이웃이 그 노드의 계산 그래프를 정의함.
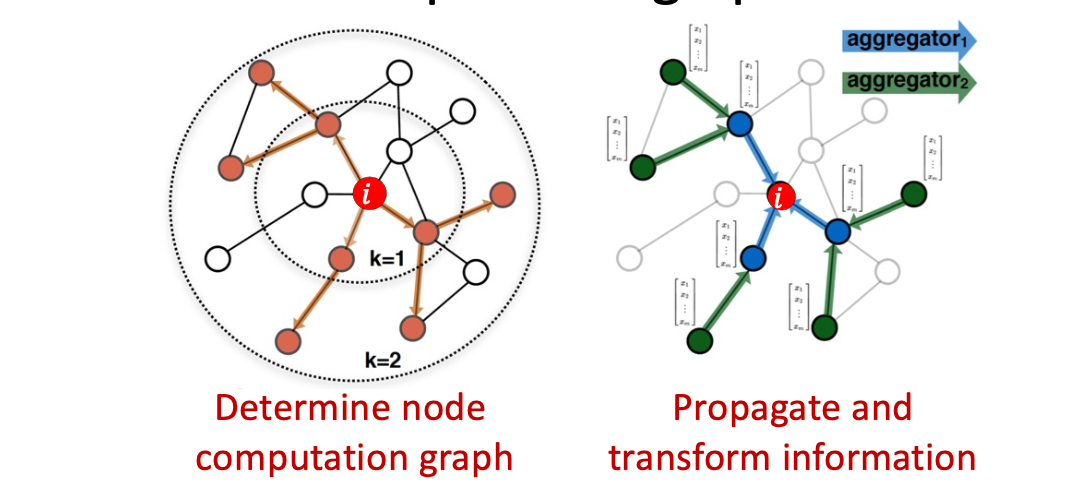
- 노드 별 계산 그래프 정의 : 중심 노드 i 를 기준으로 k-hop 범위 내의 이웃 노드들이 해당 노드의 정보 업데이트에 참여한다. (k-hop neighborhood)
- 정보 전파 및 변환 : 이웃 노드들의 정보를 message passing과 aggregation을 통해 통합함.
Recap : Aggregate from Neighbors
각 노드는 자기 주변의 이웃으로부터 정보를 받아서 자신의 벡터 표현을 업데이트한다.
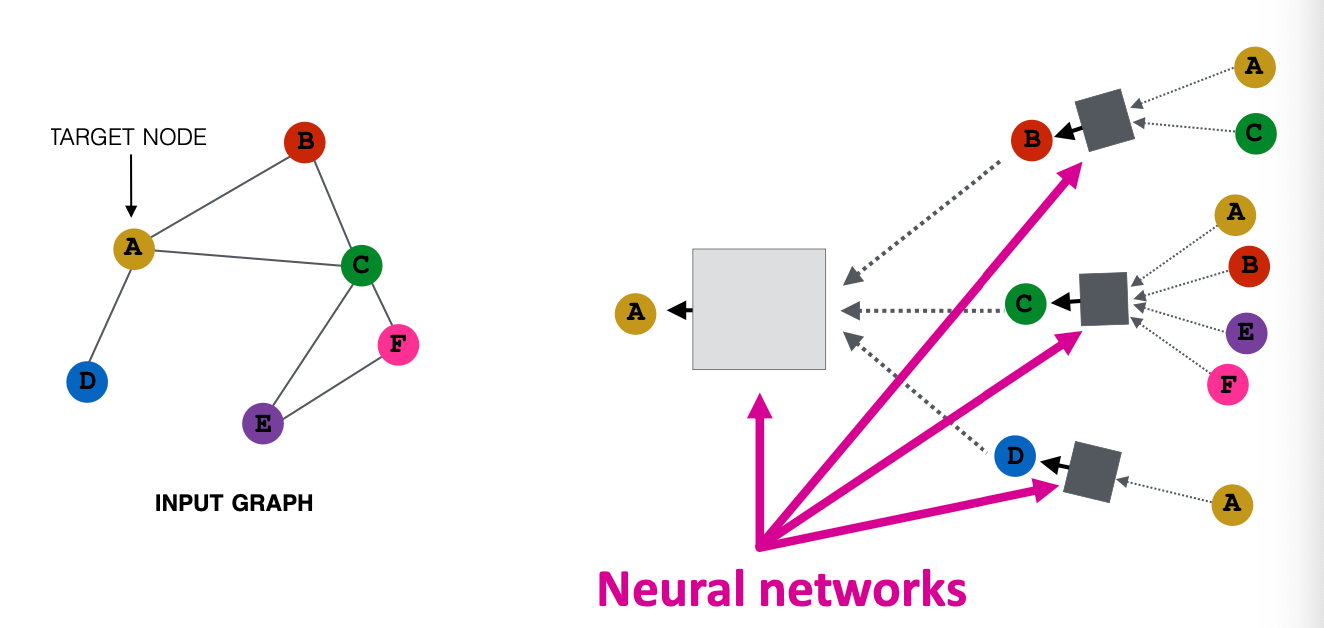
Recap : Aggregate Neighbors
- 네트워크에서 각 노드는 자신의 이웃으로부터 정보를 단계적으로 집계한다.
- 모든 노드는 자신의 연결관계 (이웃 구조)를 바탕으로 독립적인 정보 집계 과정을 가진다.
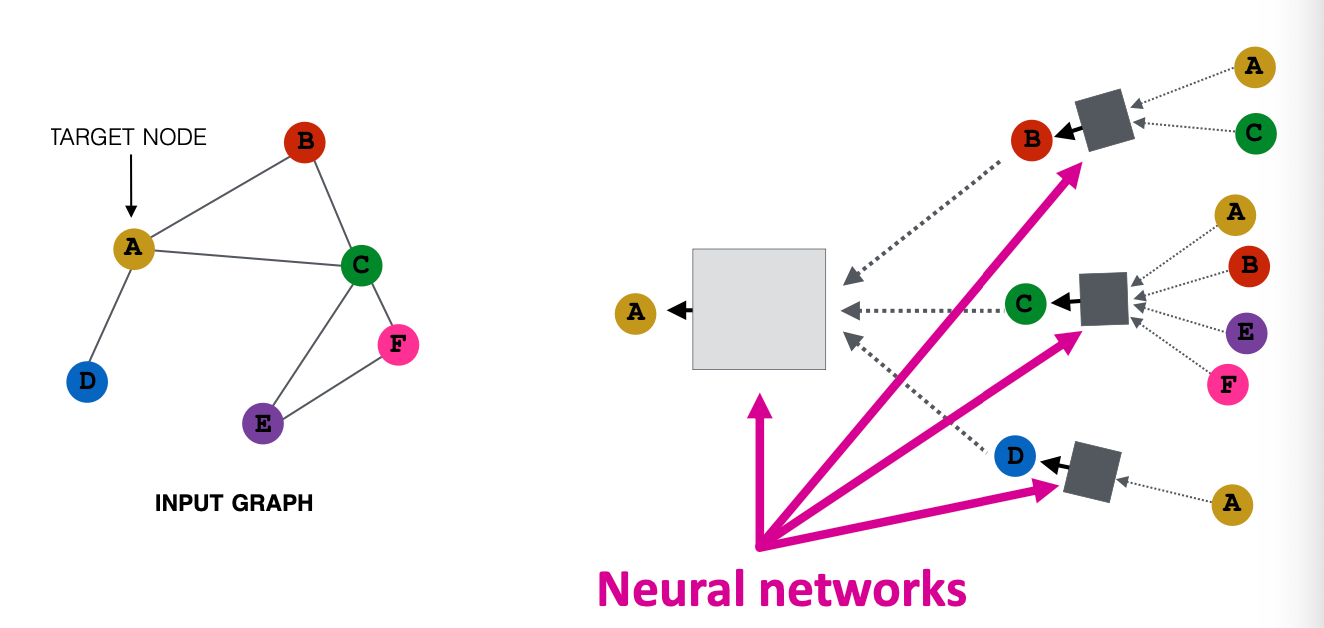
→ GNN은 하나의 큰 그래프를 여러 개의 노드별 지역 계산 그래프로 분해하여, 각 노드가 이웃의 정보를 단계적으로 집계하고 학습하는 구조
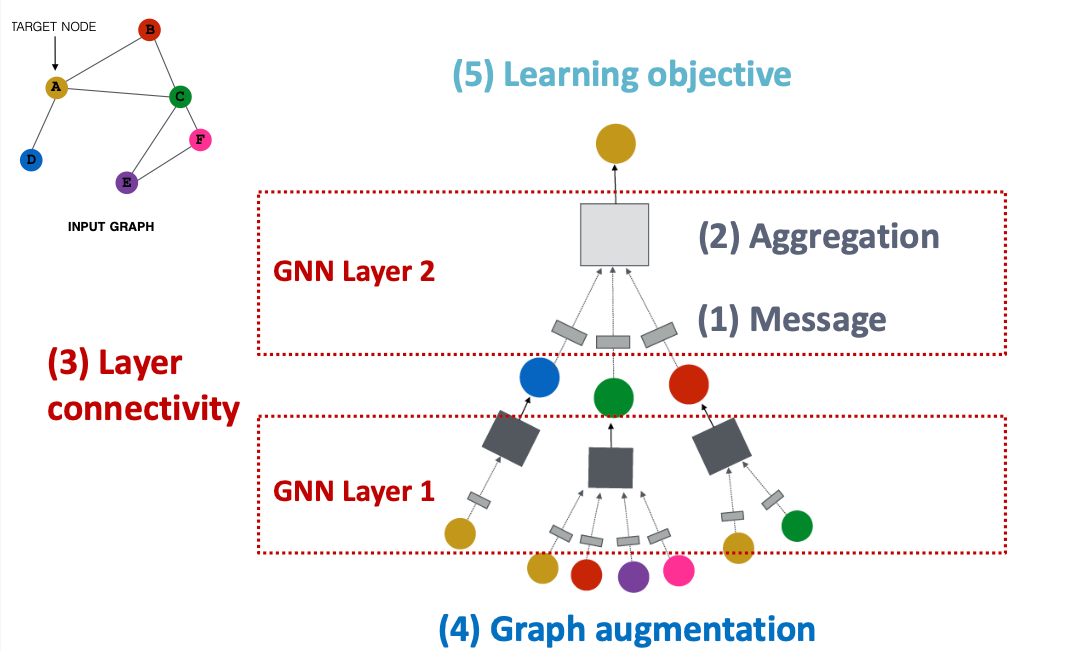
A General GNN Framework
: 이웃 간 메시지 전달과 집계를 반복하면서, 층을 쌓아 더 넓은 그래프 정보를 학습하고, 최종적으로 학습 목표를 통해 예측을 수행하는 신경망 구조임.
메시지 전달 → 집계 → 층 연결 → 그래프 확장 → 학습 목표
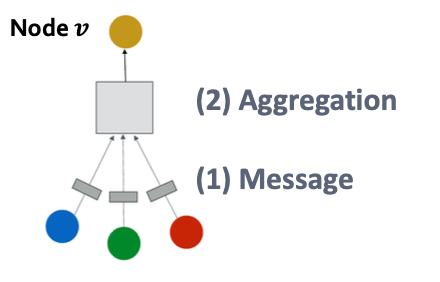
1. A Single Layer of a GNN
GNN Layer = Message + Aggregation
- 하나의 GNN layer은 이웃으로부터 메시지를 받고 → 그것을 집계 → 자신의 임베딩 업데이트
- ex) GCN, GraphSAGE, GAT, …
A Single GNN Layer
- compress a set of vectors into a single vector
- 2-step process
1. Message : 각 이웃 노드가 자신의 정보를 중심 노드에게 보냄
2. Aggregation : 중심 노드가 이웃들로부터 받은 메시지를 통합해서 자신의 새로운 임베딩 생성
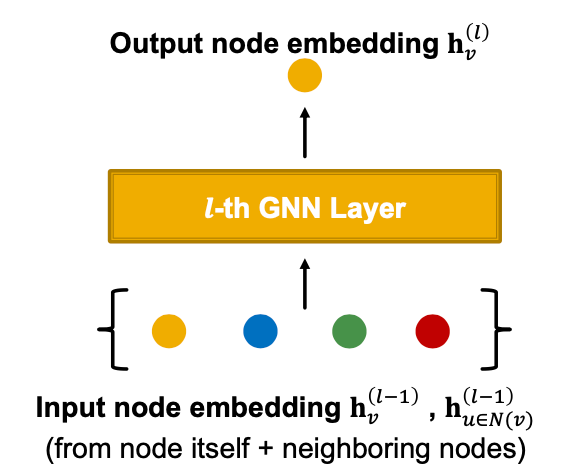
자기 노드의 이전 표현 + 이웃 노드들의 이전 표현 = 다음 레이어의 입력
Message Computation
(1) Message computation (메시지 계산)
각 노드는 자신이 가진 정보를 이웃에게 전달할 메시지를 만든다.
- Message Function :
- MSG function Example : A Linear Layer
(2) Aggregation (집계 단계)
각 노드 는 이웃 노드들 로부터 받은 메시지들을 모아서 자신의 새로운 표현을 만든다.
- Agg Example : Sum(·), Mean(·), or Max(·) aggregatorex) $h_v^{(l)} = Sum(\{ m_u^{(l)} , u \in N(v) \})$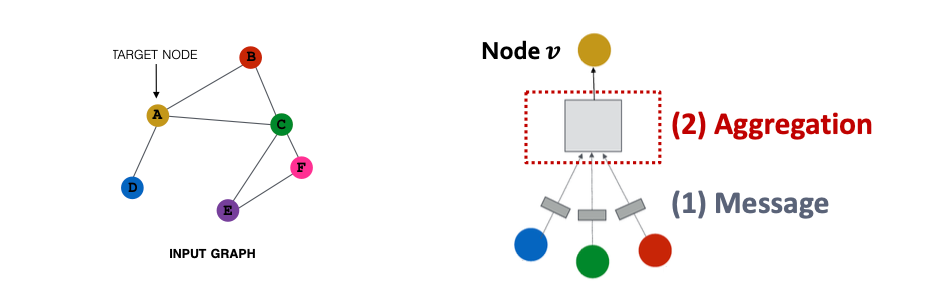
Message Aggregation 에서의 문제점
문제점 : 노드 자기 자신의 정보가 사라질 수 있다 → 계산이 이웃 노드 정보에만 의존하게 됨.
해결방법: 를 계산할 때, 자기 자신의 정보도 메시지로 포함시켜서 함께 집계하도록 하자
💬 (1) Message
자기 자신 노드 도 메시지를 생성한다.
보통, 이웃 노드와 자기 자신에 대해 서로 다른 가중치 행렬을 사용한다.
- For neighbors:
- For self node:
🔗 (2) Aggregation
이웃 노드들의 메시지를 모두 집계한 뒤, 자기 자신의 메시지도 포함 시켜 최종 노드 표현을 만든다.
이때, 덧셈이나 벡터 연결 방식을 사용한다.
→ GNN은 이웃의 정보 뿐만 아니라 자기 자신의 정보도 포함해야 함!!
→ 이웃의 메시지 + 자기 자신의 메시지 = 새로운 노드 표현
A Single GNN Layer
자기 자신의 메시지를 포함시켰을 때의 GNN layer
- 하나의 GNN layer은 세 단계로 구성된다. (1) Message : 각 노드가 자신의 feature로부터 메시지를 계산한다. 이웃 노드 + 자기자신 모두 메시지를 만든다. (2) Aggregation : 이웃 노드들의 메시지를 모아 새로운 표현을 만든다. 중심 노드 는 이웃들의 메시지와 자신의 메시지를 집계해서 새로운 노드 표현 생성
- Nonlinearity (activation) : 모델의 표현력 향상
$\sigma(\cdot)$ (e.g. ReLU, Sigmoid, etc.)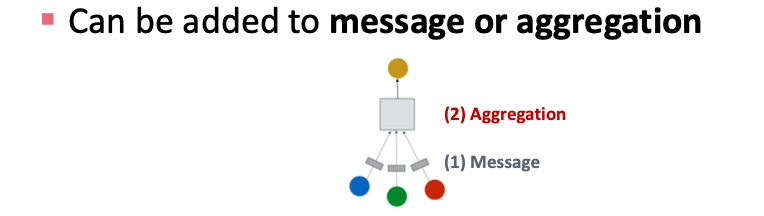
Activation (Non-linearity)
모델이 단순한 선형 계산만 반복할 시 복잡한 패턴을 학습하기 어려움
→ 각 차원 에 비선형 함수를 적용해 표현력을 높이는 것이 활성화 함수임.
- ReLU (Rectified Linear Unit)

- $\text{ReLU}(x_i) = \max(x_i,0)$
- 0보다 작으면 0, 크면 그대로 값을 통과시키는 단순한 구조
- 가장 많이 쓰이는 활성화 함수- Sigmoid
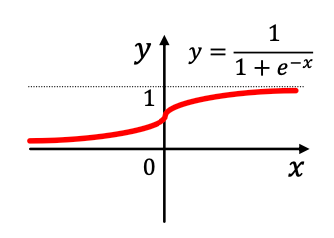
- $\sigma(x_i) = \dfrac{1}{1+e^{-x_i}}$
- 출력이 0~1 사이로 제한됨
- 주로 확률값 표현이 필요한 경우 사용
- 단, 큰 입력 값에서 gradient 가 0으로 수렴하는 포화 문제- Parametric ReLU (PReLU)
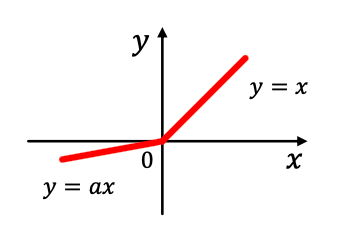
- $\text{PReLU}(x_i) = \max(x_i,0) + a_i\min(x_i,0)$ - $a_i$는 학습가능한 파라미터 - 음수 영역 기울기를 0 대신 $a_i$로 둬서 ReLU의 한계를 보완 - 경험적으로 ReLU보다 성능이 좋음. (음수 영역도 조금은 통과시킴)
Classical GNN Layers → GCN / GraphSAGE / GAT
1. GCN
GCN 이란?
→ CNN의 그래프 버전임. 이웃 노드의 정보를 평균내고, 그 결과에 가중치 행렬 W를 곱해서 노드의 새로운 표현을 생성한다.
How to write this as Message + Aggregation?

- : 이전 층에서의 노드 임베딩
- : 현재 층의 학습 가능한 가중치 행렬
- : 이웃 수로 나누어 평균하는 역할 (정규화)
→ 각 이웃이 동일한 비중으로 기여하도록 만듬.
- GCN에서는 자기 자신도 이웃으로 포함시켜서 함께 합산함. → 즉,
2. GraphSAGE
GraphSAGE란?
→ 이웃의 정보를 sampling하고 집계한 뒤, 자기 자신의 임베딩과 연결해서 업데이트하는 GNN 모델 .
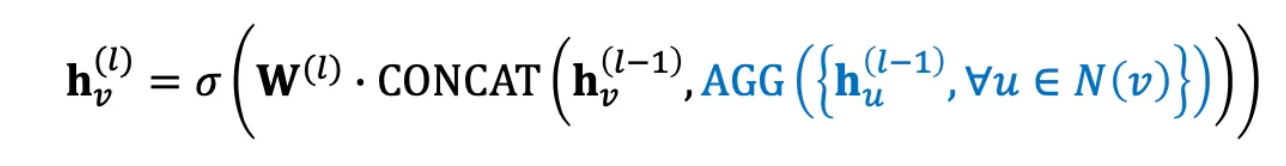
- : 이전 층의 노드 의 임베딩
- : 이전 층의 이웃 노드 의 임베딩
Two-stage aggregation
Stage 1️⃣ — 이웃으로부터 집계 (Aggregate from neighbors)
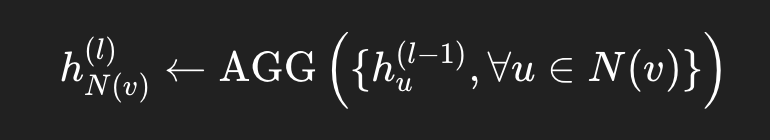
👉 주변 이웃 노드들의 임베딩을 평균/합/최댓값 등으로 집계(aggregate)
Stage 2️⃣ — 자기 자신과 결합 (Combine with self-node)

자기 정보와 이웃 정보를 연결(CONCAT) 후, 가중치 곱하고 비선형 활성화를 적용해 새로운 임베딩 생성
Neighbor Aggregation
GraphSAGE는 다양한 집계 함수 사용 가능함. 🔹 (1) Mean Aggregator → 각 이웃들의 균등 가중 평균
🔹 (2) Pool Aggregator → 이웃 정보를 비선형 변환 후 집계하는 방식 (중요도 다름)
🔹 (3) LSTM Aggregator → 순서를 고려한 집계
L2 Normalization
GraphSAGE에서는 각 층의 노드 임베딩 $h_v^{(l)}$에 l2 정규화를 적용할 수 있음. 여기서
→ 벡터 크기를 통일시켜 안정적인 학습 유도
GCN vs GraphSAGE
| 항목 | GCN | GraphSAGE |
|---|---|---|
| 자기 노드 포함 방식 | 자기 자신을 이웃에 포함시킴 | 자기 노드 임베딩과 이웃 임베딩을 CONCAT |
| 집계 함수 | 평균(Mean) 기반 (고정) | 다양한 집계 가능 (Mean, Max, LSTM 등) |
| 샘플링 | 전체 이웃 사용 | 일부 이웃만 샘플링 가능 |
| 목표 | 전체 그래프 학습 (Transductive) | 새로운 노드도 일반화 가능 (Inductive) |
3. GAT (Graph Attention Networks)
GAT란?
각 노드가 이웃의 정보를 동일하게 평균하지 않고, 학습 가능한 attention 가중치를 두어 더 중요한 이웃에게 더 높은 비중을 부여하는 방식

- : attention weight → 가 에게 얼마나 중요한가를 나타내는 값.
GCN/GraphSAGE와의 차이점?
- 기존의 GCN이나 GraphSAGE에서는 이웃의 중요도를 동일하게 취급했다. 하지만, GAT는 각 이웃의 중요도를 학습해 다르게 반영하는 그래프 신경망 → 더 중요한 관계에 더 집중하도록 !!
- (GCN의 경우 ) 즉, 모든 이웃 노드 가 동일한 비중으로 노드 의 임베딩 계산에 기여했다. 그래프의 구조적 특성 (이웃의 수) 에 기반한 고정 비율이지, 학습되는 값이 아님 !!
| 항목 | GCN / GraphSAGE | GAT |
|---|---|---|
| 가중치(α) | $\alpha_{vu} = \frac{1}{ | N(v) |
| 중요도 | 모든 이웃 동일 | 중요도가 다름 |
| 근거 | 구조적 속성(이웃 수) | 데이터 기반 학습 (attention) |
| 결과 | 단순 평균 | 가중 평균 (학습 기반) |
Not all node’s neighbors are equally important.
- attention coefficient 는 입력 데이터 중 중요한 부분에 집중하고, 덜 중요한 부분은 무시한다.
- Neural Network는 전체 데이터 중 작지만 중요한 부분에 더 많은 계산 자원을 사용해야함.
- 데이터의 어떤 부분이 중요한지는 context에 따라서 달라지며, 이는 training을 통해 자동 학습
Graph Attention Networks
Can we do better than simple neighborhood aggregation?
Can weighting factors be learned?
- 목표 : 그래프의 각 노드마다 이웃 노드에 임의의 중요도를 부여할 수 있도록 하는 것 즉, 단순히 모든 이웃을 동일하게 평균내는 대신, 어떤 이웃은 더 중요하고, 어떤 이웃은 덜 중요하다는 것을 모델이 학습하게 하는 것이 목표임 !
- 아이디어 : 그래프의 각 노드 v에 대해 어텐션(attention) 전략을 따라 임베딩 를 계산한다.
- 각 노드는 자신의 이웃들의 메시지에 대해 어텐션(attend) 을 수행함.
- 이를 통해 이웃 노드마다 다른 가중치(weight) 를 암묵적으로 부여하게 됨.
Attention Mechanism
Attention Coefficient 계산
노드 u와 v 쌍에 대해, 각각의 노드 임베딩을 비교해서 어떤 이웃이 더 중요한가를 나타내는 attention coeffiecient를 구한다.
- attention coefficient :

: A의 메시지가 B에게 얼마나 중요한가를 나타내는 attention score
→ 이 값이 더 클수록 A의 정보가 B의 표현 학습에 더 크게 반영된다.
normalize
- 를 정규화 해서 최종 어텐션 가중치 로 만든다
- softmax function →
weighted sum
최종으로, 각 노드 v의 표현은 모든 이웃의 임베딩을 가중합하여 계산한다.
즉, 중요도가 높은 이웃의 정보는 더 크게 반영되고, 덜 중요한 이웃은 덜 반영됨.

노드 A의 이웃 (B,C,D) 각각에 대해 다른 가중치를 부여해 A의 표현을 계산하는 방법
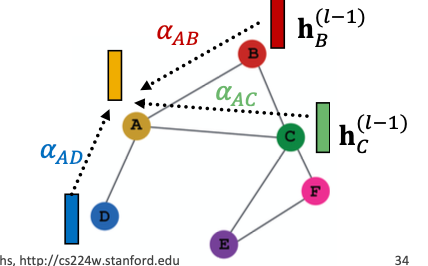
What is the form of attention mechanism a?
→ 두 노드의 임베딩을 concat + linear layer 통과 → 유사도 계산
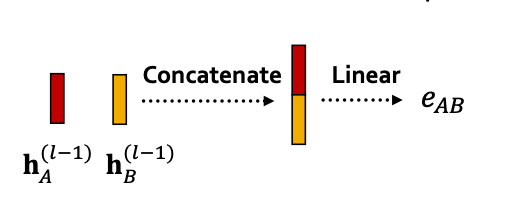
- a 안의 파라미터 들은 학습 가능함.
- 가중치와 함께 end-to-end 방식으로 공동학습 된다.
→ 네트워크는 ‘어떤 이웃이 중요한지’를 데이터로부터 자동으로 배울 수 있다.
Multi-head attention : Stabilizes the learning process of attention mechanism
단일 어텐션은 한 가지 관점으로만 이웃 노드의 중요도를 학습하지만, 멀티헤드는 서로 다른 가중치 집합으로 여러 관점에서 이웃 관계를 학습할 수 있다.

- Aggregation (출력 결합)
- 모든 헤드의 출력을 하나로 합친다 ( 결합 방법 : concat 또는 sum)

→ 여러 어텐션 헤드가 다양한 관점에서 이웃을 바라보게 함으로써 학습 안정성과 성능 향상을 동시에 얻음
Benefits of Attention Mechanism (어텐션의 장점)
- 핵심 이점
- 서로 다른 이웃 노드에 대해 다른 중요도 값을 부여할 수 있다. (중요도 다르게 학습 가능)
- 계산 효율성 (Computationally efficient)
- 어텐션 계수의 계산은 그래프의 모든 엣지에서 병렬화 가능함.
- 각 노드별로 aggregation 연산 또한 병렬 수행 가능
- 저장 효율성 (Storage efficient)
- sparse matrix 연산을 사용 → 저장공간이 O(V+E)에 비례함
- 그래프 크기와 무관하게 학습 파라미터 수는 고정되어 있음
- 지역성(Localization)
- GAT는 로컬 이웃에 대해서만 어텐션 수행
- 전역 그래프 구조를 전부 보지 않아도 됨
- 귀납적 성질 (Inductive capability)
- edge-wise로 작동하는 메커니즘
- 새로운 노드나 새로운 그래프에도 적용할 수 있음 → 전체 그래프 구조에 의존하지 않음
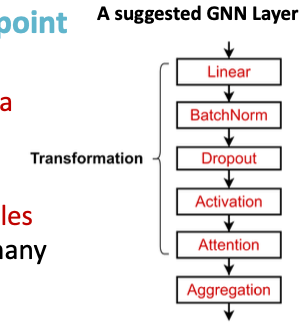
2. GNN Layers in Practice
전통적인 GNN 계층(GCN, GraphSAGE, GAT 등)은 좋은 출발점이지만, 현대 딥러닝 모듈을 포함하면 성능을 더 개선할 수 있다.
-
여러 딥러닝 구성 요소(modules) 를 GNN 계층 내부에 통합 가능하다.
-
예시 구조 (오른쪽 그림):
1. Linear (선형변환)
2. BatchNorm (정규화)
3. Dropout (과적합 방지)
4. Activation (활성화)
5. Attention (메시지 중요도 조절)
6. Aggregation (이웃 정보 집계)
Batch Normalization (배치 정규화)
→ 노드 임베딩을 정규화하여 학습 안정성과 수렴 속도 향상
Dropout (드롭아웃)
→ 신경망을 정규화하여 overfitting 방지
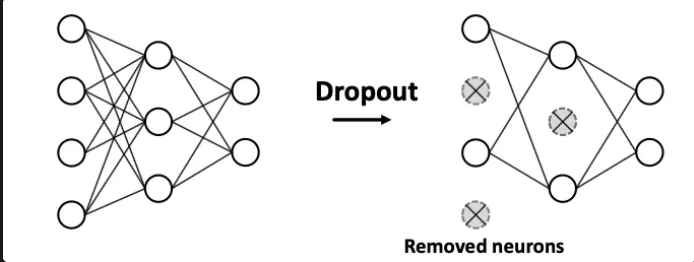
Dropout for GNNs (GNN에 적용된 드롭아웃)
→ message function의 linear layer에 적용

- 이 선형 변환 중 일부 뉴런을 드롭아웃 시켜 메시지 전달 단계에서의 정보 과적합을 방지
→ 메시지를 구성하는 피처 일부를 랜덤하게 꺼서 보다 일반화된 메시지 표현을 생성
GNN Layer 설계 요약
현대 딥러닝 모듈(BatchNorm, Dropout, Attention 등)을 GNN 계층 안에 통합하면 성능 향상 및 안정화 도움
3. Stacking Layers of a GNN
Stacking GNN Layers
GNN layer들을 어떻게 연결해서 하나의 GNN을 만들까?
- 순차적으로 쌓기 (여러 GNN Layer을 위로 차례로 쌓기)
- Skip Connection 추가하기 (이전 층의 출력을 나중 층으로 직접 전달하는 연결 방식)
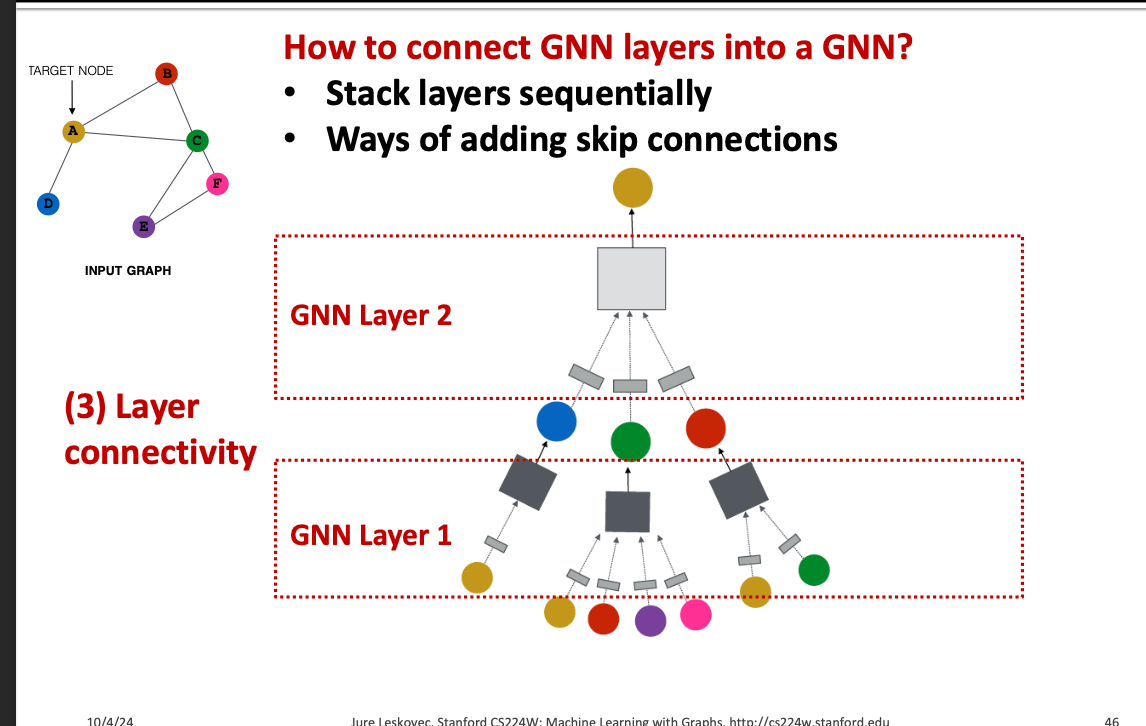
How to construct a Graph Neural Network?
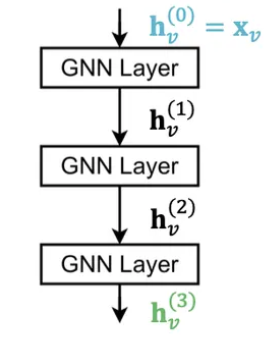
- 표준적인 방법 : GNN Layer를 순차적으로 쌓기
- Input : 초기 노드 특징
- Output : L개의 GNN Layer를 거친 후의 노드 임베딩
The Over-smoothing Problem = stacking many GNN layers
- GNN을 너무 많이 쌓을 때 생기는 문제
- 그래프 전체의 노드 임베딩이 점점 비슷해져서 결국 모든 노드 표현이 거의 같은 값으로 수렴하는 현상
Receptive field : 특정 노드 임베딩을 결정하는 이웃 노드들의 집합 (수용 영역)
- GNN Layer 깊이에 따른 변화
- K-layer GNN에서는, 각 노드는 K-hop 이웃(K-hop neighborhood) 의 정보를 수용
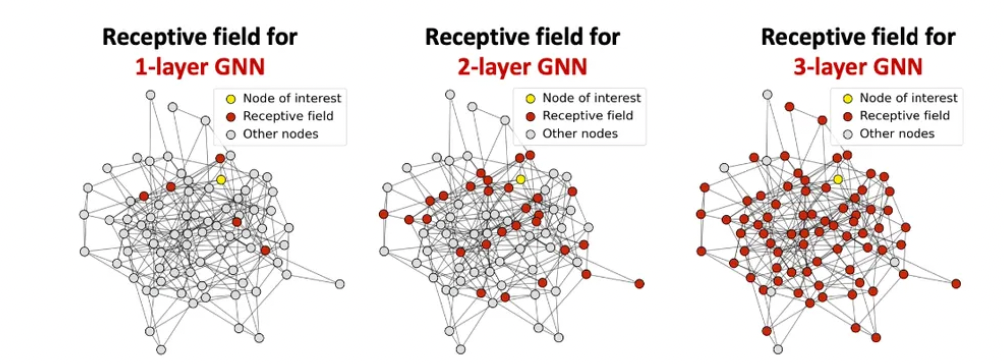
Receptive Field Overlap
두 노드가 서로 다른 노드여도 GNN layer가 깊어질수록 공유하는 이웃이 급격히 늘어남.
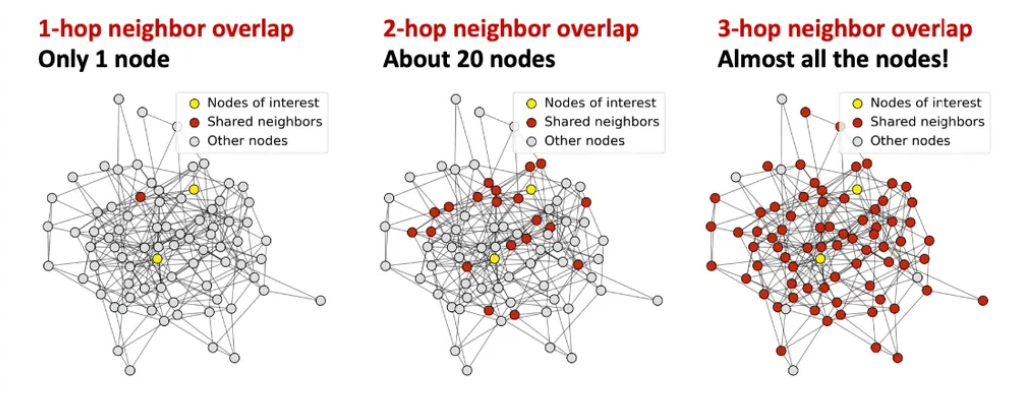
즉, GNN이 깊어질수록 서로 다른 노드라도 같은 이웃 정보를 공유하게 되어, 임베딩이 비슷해지는 현상이 나타남.
Over - smoothing이 발생하는 이유
- Over-smoothing 문제는 수용영역의 중첩(Overlap) 으로 설명할 수 있다.
- 노드 임베딩은 그 노드의 receptive field 로 결정된다.
- 만약 두 노드가 거의 같은 receptive field 를 가진다면, 두 임베딩 도 매우 비슷해진다.
GNN layer를 너무 많이 쌓으면 → 모든 노드가 매우 겹치는 receptive field 를 갖게 됨 → 임베딩이 거의 동일해짐 → Over-smoothing 발생
Design GNN Layer Connectivity
What do we learn from the over-smoothing problem?
Lesson 1: GNN Layer를 추가할 때 주의
- CNN처럼 무조건 깊게 쌓는 게 GNN엔 도움이 되지 않는다. (즉, 이미지 분야처럼 “깊을수록 좋다”가 아님.)
- Step 1: 문제를 해결하는 데 필요한 receptive field 크기를 먼저 분석하라. (예: 그래프의 지름(diameter)을 계산해서 몇 hop까지 필요할지 확인)
- Step 2: 필요한 정도보다 조금 더 큰 GNN layer 수 L 을 설정하되,너무 과하게 크지 않도록 한다.
그럼 GNN layer 수가 작을 때는 어떻게 표현력을 높일 수 있을까?
Expressive Power for Shallow GNNs
How to make a shallow GNN more expressive?
Solution 1: 각 Layer 내부의 표현력 강화
- 한 GNN layer 안의 “변환(Transformation)”과 “집계(Aggregation)”를 더 강력하게 만든다.
- 기존 GNN에서는 transformation 또는 aggregation이 보통 선형 변환(Linear layer) → 여러 층(예: 3-layer MLP) 을 넣어서 더 깊고 복잡한 변환을 수행할 수 있다.
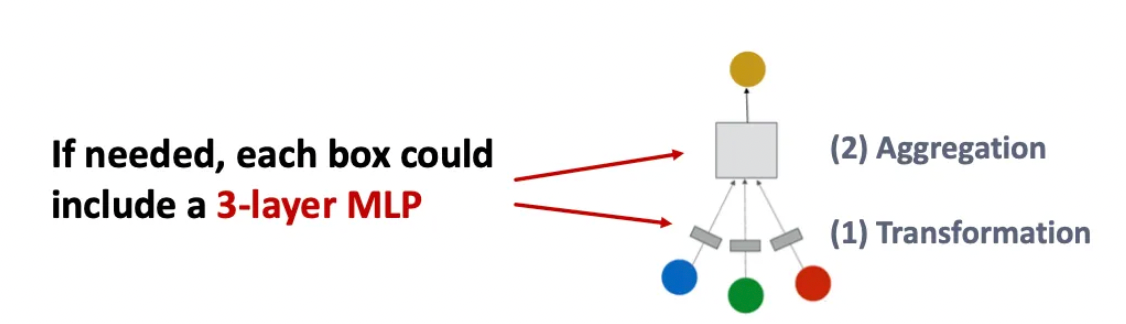
Solution 2: 메시지를 전달하지 않는 Layer 추가
- GNN layer 외부에도 MLP 같은 비전파형 신경망층을 추가할 수 있음.
- Pre-processing layer (사전 처리층)
- 노드의 원본 피처(예: 이미지, 텍스트)를 임베딩 형태로 변환할 때 사용.
- 즉, 그래프 입력 전에 피처 인코딩 역할.
- Post-processing layer (사후 처리층)
- 그래프 임베딩이 만들어진 뒤,분류(classification)나 관계 추론(reasoning)을 수행할 때 사용. - 예: 그래프 분류, 지식그래프(kb) 예측 등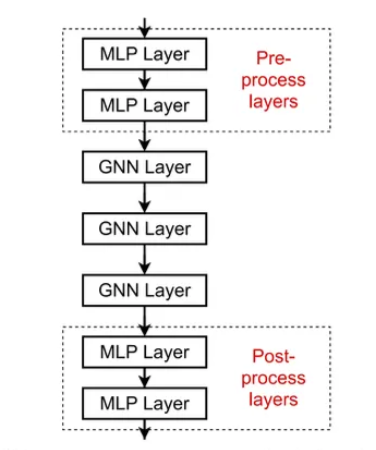
Design GNN Layer Connectivity
What if my problem still require many GNN layers?
Lesson 2: GNN에 Skip Connection을 추가하라
- Observation from Over-smoothing
- 깊은 GNN에서 초기 층의 임베딩이 오히려 노드 간 구분에 더 도움이 되는 경우가 있다.
- 하지만 layer가 많아질수록 이 초기 정보가 사라진다. → over smoothing
- Solution
- 이전 layer의 출력을 직접 연결해서 나중 layer의 임베딩 계산에 반영하자
Why do skip connections work?
Skip connections은 여러 개의 모델이 섞인 것처럼 작동한다.
- N skip connections이 있을 경우 가능한 경로가 2^N개나 된다.
- 각각의 경로는 서로 다른 깊이의 GNN을 의미하고, 그 결과 얕은 GNN과 깊은 GNN 조합 효과
→ GNN이 한 모델로 여러 깊이의 표현을 동시에 학습하게 된다!
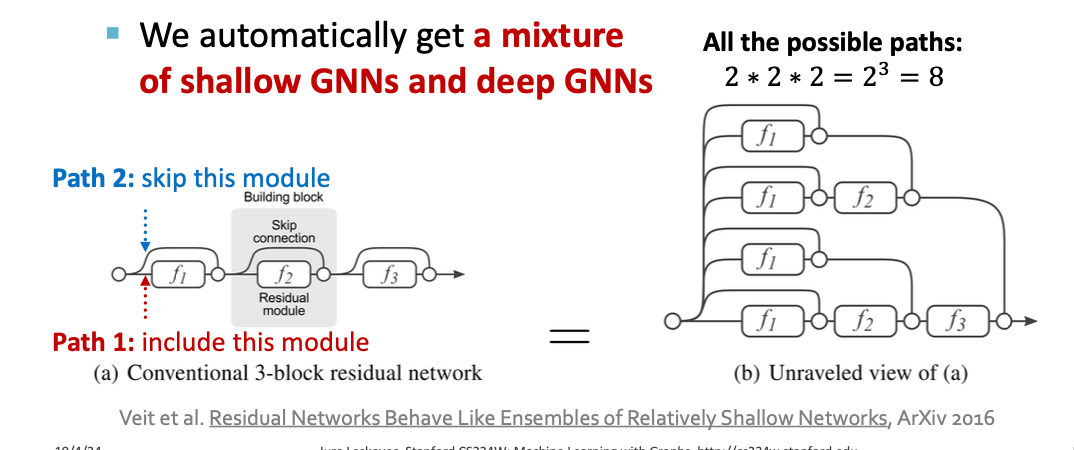
Example : GCN with Skip Connections
GNN에서 발생하는 over smoothing 문제를 완화하기 위해 이전 층의 출력을 다음 층에 직접 더해줌.
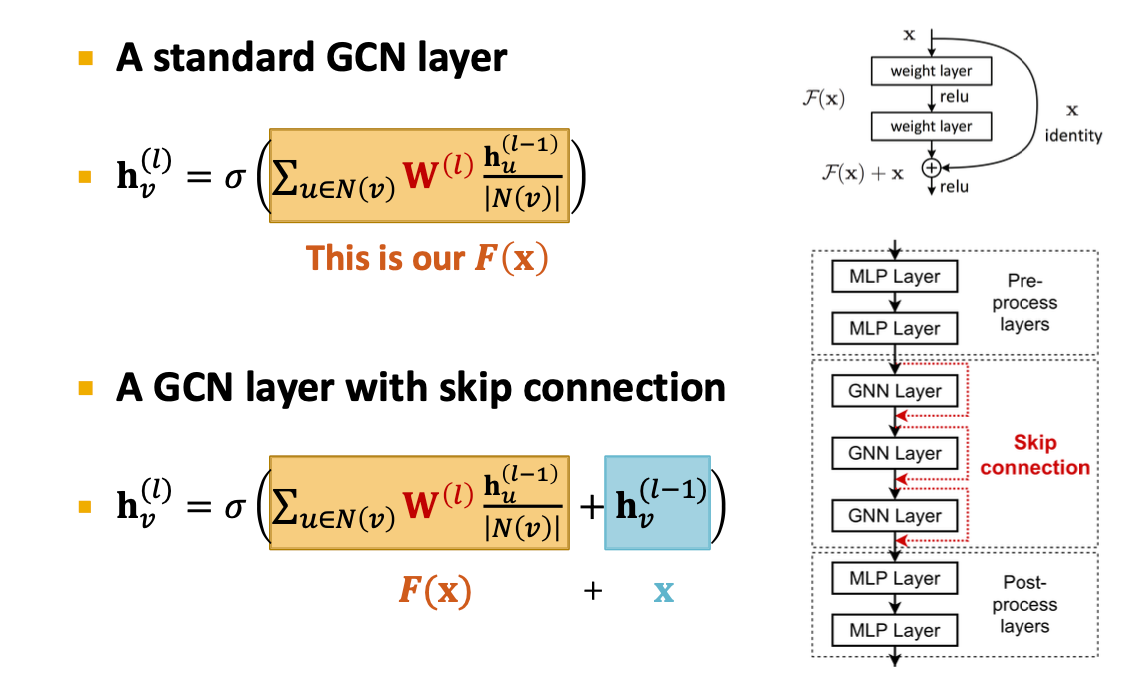
→ 이전 층의 자기자신 값을 직접 더해준다 (x를 추가함)
→ 깊은 네트워크에서도 초기 정보가 유지되어 over-smoothing을 완화시킬 수 있다.
Other Options of Skip Connections
- 이전 층의 출력을 다음 층에 바로 더하는 것 외에도 모든 중간층의 출력을 한꺼번에 최종층에서 결합하는 방식
- 초기 정보 손실 방지
- over smoothing 완화
- 깊은 GNN에서도 안정적 학습을 가능하게 함.
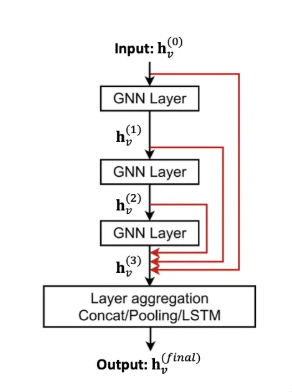
4. Graph Manipulation in GNNs
그래프 자체를 어떻게 조작해서 GNN학습을 개선할 수 있을까?
GNN은 단순히 네트워크 구조 위에서만 학습하는 것이 아니라, 그래프의 구조나 피처를 바꾸는 것도 학습 성능에 큰 영향을 준다.
General GNN Framework
- 원래 입력 그래프는 GNN이 실제 계산하는 그래프와 같지 않다.
- Graph feature augmentation
- 노드/엣지의 피처를 인공적으로 추가하거나 확장함
- Graph structure manipulation
- 엣지나 노드를 추가/삭제하거나, 서브그래프만 샘플링해서 사용함.
- Graph feature augmentation
Why Manipulate Graphs ?
- 지금까지의 기본 가정 : 입력 그래프 = 계산 그래프 .
- GNN은 주어진 그래프 구조 그대로 학습한다고 생각함. 하지만 이것은 항상 최적의 선택이 아님.
1️⃣ Feature Level (피처 수준)
- 입력 그래프에 피처(feature) 가 부족한 경우 → feature augmentation (특성 보강) 필요.
2️⃣ Structure Level (구조 수준)
- 그래프가 너무 희소(sparse) → 메시지 전달이 비효율적. → 엣지/가상노드 추가 필요.
- 그래프가 너무 조밀(dense) → 메시지 전달에 너무 많은 계산이 필요함. → 일부 이웃만 샘플링해서 사용.
- 그래프가 너무 큼(large) → GPU 메모리에 한 번에 안 들어감. → 서브그래프(subgraph) 단위로 나누어 학습해야 함.
요약:
“입력 그래프 자체가 최적의 계산 그래프일 가능성은 매우 낮다.”
Graph Manipulation Approaches (그래프 조작 방법)
🔸 Graph Feature Manipulation
- 입력 그래프에 피처가 부족할 때 → Feature Augmentation → 예: 노드의 속성 추가, 중심성/차수/클러스터링 계수 등 파생 피처 생성.
🔸 Graph Structure Manipulation
-
그래프가 너무 희소할 때 → 가상 노드(virtual node)나 가상 엣지(edge) 추가.
(예: 중앙 허브 노드 추가해서 모든 노드와 연결)
-
그래프가 너무 조밀할 때 → 메시지 전달 시 이웃 샘플링(neighbor sampling)
(대표적으로 GraphSAGE에서 사용됨)
-
그래프가 너무 클 때 → 전체 그래프 대신 서브그래프(subgraph) 만 샘플링해서 임베딩 계산
(예: Cluster-GCN, GraphSAINT 등)
1. Add Virtual Nodes / Edges
희소 그래프에서의 GNN 성능 개선 방법
그래프가 너무 엮이지 않은 상태일때 (노드 간 연결이 적을 때) 메시지 전달이 비효율적이므로 이를 개선하기 위한 가상노드와 가상 엣지 사용!!
1. Add virtual edges
2-hop 이웃(두 단계 떨어진 노드) 을 새 엣지로 연결하는 방법
- 기존에는 인접 행렬 A를 사용했지만, 이제 A + A^2 형태로 계산함.
ex)

기존 엣지는 저자가 쓴 논문 관계였다면, 가상엣지를 추가하므로써 ‘같은 논문을 쓴 저자들끼리 연결’
→ 2-hop 이웃 간의 정보 흐름이 생겨서 희소 그래프의 메시지 전달 효율이 향상된다.
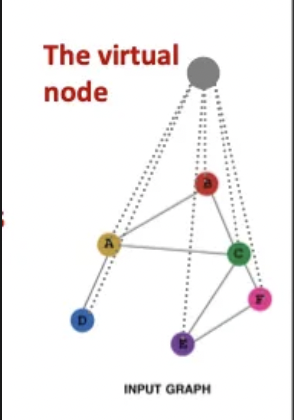
2. Add virtual nodes
그래프 전체에 모든 노드와 연결된 중앙 허브 노드를 추가함.
- 원래 희소 그래프에서는 어떤 두 노드 간 최단 거리가 10일수도 있음
- 그런데 가상 노드를 추가하면 모든 노드가 그 가상 노드에 연결되므로 두 노드 간 거리가 2로 줄어듬.
- Node A → Virtual Node → Node B2
- 장점 : 멀리 떨어진 노드 간 정보 전달이 쉬워지고 희소 그래프에서 메시지 전달이 크게 개선된다.
2. Node Neighborhood Sampling (노드 이웃 샘플링)
기존 접근 : 모든 이웃 노드로부터 메시지를 전달받음 → 모든 이웃들의 임베딩을 합쳐서 다음 레이어 표현 계산
문제 : 그래프가 너무 크거나 조밀할 때
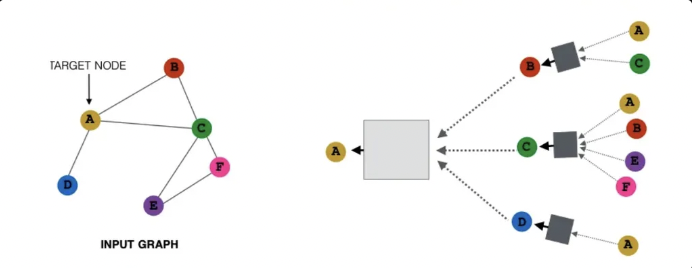
new idea : 메시지 전달 시 일부 이웃만 무작위로 샘플링 해서 사용하자 → neighborhood sampling
예) 무작위로 2개 이웃을 선택해서 메시지를 주고 받자
target node = A일 때, B와 D 2개만 이웃으로 선택해서 메시지를 주고 받음
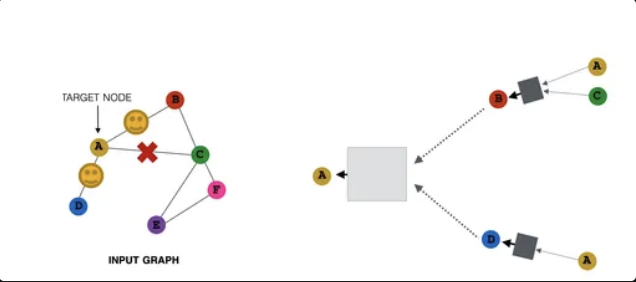
다음 단계에서는 이전과 다른 노드들 (C,D)를 선택해서 A로 메시지를 보냄.
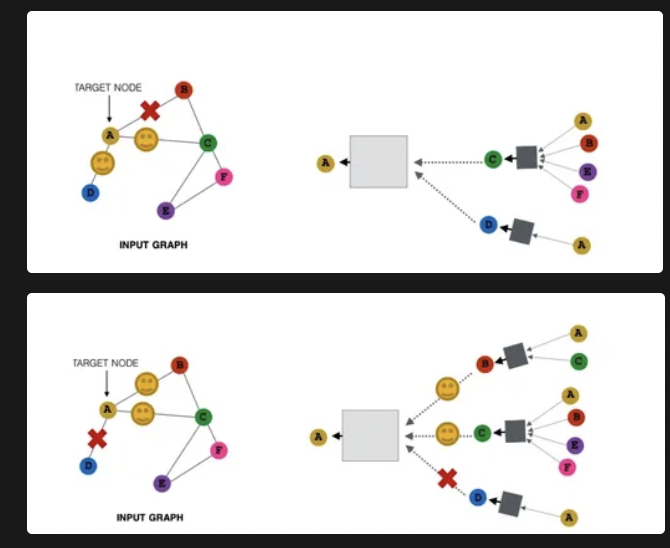
여러 번 샘플링해서 평균적으로 보면, 모든 이웃을 썼을 때와 거의 동일한 임베딩 결과를 얻을 수 있음.
장점 : 계산량 감소, 실질적 성능 good
→ A의 모든 이웃들이 존재 = 매번 다른 샘플링 결과를 통합한 모습 ⇒ 결과적으로, 모든 이웃의 정보를 어느정도 반영한 효과 !!
Summary of the lecture
A general perspective for GNNs
- GNN Layer :
- Transformation + Aggregation
- Classic GNN Layers : GCN, GraphSAGE, GAT
- Layer connectivity
- Deciding number of layers
- Skip connections
- Graph Manipulations
- Structure manipulation
