1.2 Valuation By Monte Carlo Simulation

Woohyuk Choi·2022년 6월 21일

금융공학

금융상품 가치 측정

목록 보기

2/6

🏋️‍♀️Basic

Option의 가치는 그것의 Discounted Payoff(DPO)의 위험 중립적 (risk-neutral) 기댓값이다.

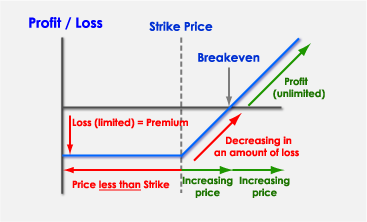
✏️European-Style-Option의 예시

C_0,_j =\exp(-\int_{0}^{T} r_u du) C_T,_j =\exp(-rT)C_T,_j

위의 식은 만기일 $T$ 에 $C_T$ 를 내야 하는 European-Option을 가정했을 때, $j$ 번째 simulation 시행에서 나타나는 $C_0$ 의 값입니다.

이걸 estimator로 나타내면..

\hat{C_o}=\frac 1 M \displaystyle\sum_{i=1}^M C_0,_j

가 되고, Standard Error(SE)는

SE(\hat{C_o})=\frac 1 {\sqrt M} \sqrt {\frac 1 {M-1} \displaystyle\sum_{i=1}^M(C_0,_j - \hat{C_o})}

이 됩니다. 뒤에 있는 Sqrt 부분은 $SD(\hat{C_o})$ 인 것을 눈치챌 수 있어요!

여기까지의 내용은 학부 2학년에서 배울 수 있는 내용이니까.. 내용 설명 없이 넘어가도 될 것 같고, 하나 설명할 점은 European-Option과 American-Option의 차이점입니다.

European Option : 만기 시에만 행사 가능
American Option : 만기 전에도 아무때나 행사 가능

그래서, 계산의 편의를 위해 European-Option을 가정했고, American-Option은 만기일까지의 기간 중에 얼마가 지났는지를 따져서 계산해주면 될 겁니다.

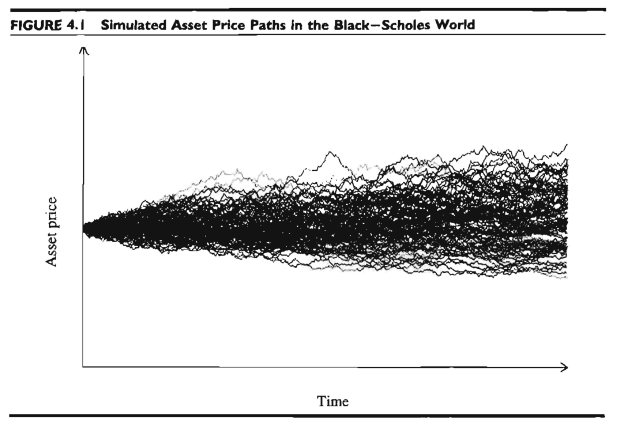
📒 Black-Scholes world에서의 GBM Process Simulation

GBM (Geometric Brownian Motion) process

dS_t = (r-\delta)S_tdt+\sigma S_t dz_t

이렇게 나타내어지죠. 이 식이 나온 배경을 살펴보면, 앞부분은 추세를 반영하는 Drift Term, 뒷 부분은 시간의 함수로 modeling 되어서 알 수 없는 움직임을 반영한 Diffusion Term이 되는 겁니다!

따라서, 이 때 $r$ 은 주가의 기대 수익률, $\delta$ 는 배당 수익률, $\sigma$ 는 주가 수익률의 Annual Volatility(1년 단위의 변동성)입니다.

이 Stochastic Process를 Ito's Lemma를 이용해서 풀어봅시다!

Ito's Lemma :

df(t,X_t) = \frac {\partial f(t,X_t)} {\partial t} dt \, +\frac {\partial f(t,X_t)} {\partial X_t} dX_t + \frac 1 2 \frac {\partial^2 f(t,X_t)} {\partial X_t^2} (dX_t)^2

이걸 이용하고, 양변에 log를 취해봅시다.. (귀찮음)

dlog(S_t)\, =\, \frac 1 {S_t} (dS_t) \, - \frac 1 2 (\frac 1 {S_t})^2 \, (dS_t)^2

이렇게요! 그래서 이걸 풀면..

S_T = S_0 \exp ((\alpha - \delta - {\frac 1 2} \sigma^2)T + \sigma Z_T)

이걸 이용하면 Black-Scholes의 가정을 유도할 수 있는데,

Black-Scholes' Model의 가정

주가의 로그 수익률은 정규 분포를 따른다.

주가는 Log Normal Distribution을 따른다.

얘는 횟수를 $M=100$ 으로 하고, $S=100, \sigma = 20/cent , r = 6/cent , T = 1 yr , N = 365$ 로 가정..

Call price의 Estimator를 얻기 위해, 우리는 다음 식을 사용할 것입니다. (Generalized)

\hat{C_o} = \exp (-rT) \frac 1 M \displaystyle\sum_{i=1}^M \max (0, S_T,_j - k)

💰Example - Pricing a EU-Call Option Monte Carlo Sim.

Pseudo-code

initialise_parameter { K, T, S, sig, r, div, N, M }

{ precompute constants }

dt = T/N
nudt = (r-div-0.5*sig^2)*dt
sigsdt = sig*sqrt(dt)
lnS= ln(S)

sum_CT = 0
sum_CT2 = 0

for j - 1 to M do ( for each simulation )

lnSt = lnS

	for i = 1 to N do ( for each time step )
   	epsilon = standard_normal_sample
       lnSt = lnSt + nudt + sigsdt*epsilon (evolve the stock price)
     next i
     
     ST = exp(lnSt)
     CT = max( 0, ST - K)
     sum_CT = sum_CT + CT
     sum_CT2 = sum_CT2 + CT*CT
     
   next j
   
   call_value = sum_CT/M * exp(-r*T)
   SD = sqrt( ( sum_CT2 - sum_CT*sum_CT/M) * exp(-2*r*T) / (M-1) )
   SE = SD/sqrt(M)

Woohyuk Choi

Financial Engineering / Mathematics / Music

이전 포스트

1.1 Monte Carlo Simulation , Intro

다음 포스트