개념 설명

이번 글에서는 뒤에서 배울 'Hedging'의 필요성을 분석하는 과정을 거쳐볼 거예요.
제목에서 사용된 'Antithetic'이라는 단어는 서로 상반됐다~ 라는 의미를 가지는데,
이를 수식으로 나타내기 위해서 두개의 Asset, $S_1$과 $S_2$에 대한 서로 다른 Option을 생각해봅시다. 얘네 둘은 현재가는 같고, 서로 완전히 상반 관계를 가지고 있는 (Perfectly negatively correlated) Option이라고 두면,

이렇게 수식을 둘 수 있겠죠!
여기서 우리가 떠올릴 수 있는 것은, 각각의 option에 대한 pay-off보다는 둘을 합쳐서 portfolio를 만들어버리면.. 그 variance가 줄어들게 된다는 거예요. (상쇄될거니까)
우리는 가치투자를 할 때 수익률도 중요하지만, 나의 자산에 대한 volatility를 줄이는, 즉 안정성이 꽤나 중요하다는 것을 알고 있기 때문에, 이러한 특징이 꽤나 도움이 된다는 것을 눈치챌 수 있을 거예요.

이 pay-off에 대한 variance가 매우 큰 이유는 행사 가격(strike price) 아래에 있는 자산 가격에 대해 확률의 'large spike'가 생기기 때문인데, 이러한 스파이크를 없애고, variance를 줄이기 위한 것이 바로 Hedge portfolio입니다.

위의 내용을 수식으로 정리해볼까요?
Simulated 된 pay-off는

이렇게 될 것 같네요. 서로 약간 pair 느낌이 나죠?

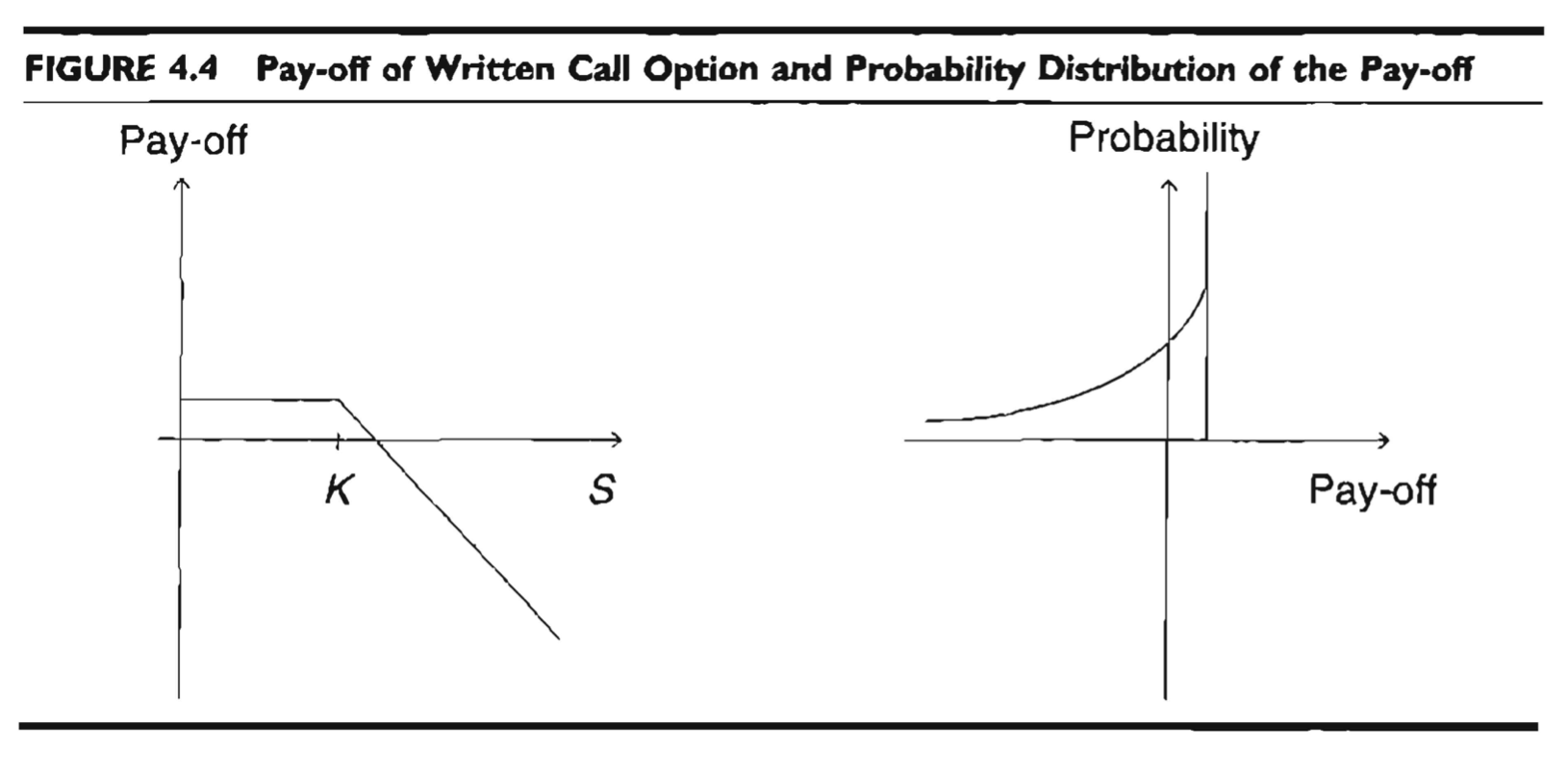
위 그래프를 보면, Pay-off가 $S=K$ 일 때까지는 일정하게 유지되다가 쭉 내려가는 걸 볼 수 있어요.
확률에 대해서는 아까 언급했던 large spike를 볼 수 있죠?

그럼 얘를 코딩해봅시다.

Example - Pricing a European Call Option by Monte Carlo Sim. with Antithetic Variance Reduction

• pseudo-code

initialise_parameters {K, T, S ,sig, r, div, N, M}

{precompute constants}

dt = T/N
nudt = (r-div-0.5*sig^2)*dt
sigsdt = sig*sqrt(dt)
lnS = ln(S)

sum_CT = 0
sum_CT2 = 0

for j = 1 to M do {for each simulation}

lnSt1 = lnS
lnSt2 = lnS

	for i = 1 to N do {for each time step}
    	epsilon = standard_normal_sample
        lnSt1 += nudt + sigsdt*(epsilon)
        lnSt2 += nudt + sigsdt*(-epsilon)
     next i
     
     St1 = exp(lnSt1)
     St2 = exp(lnSt2)
     CT = 0.5*(max(0, St1 - K) + max(0, St2 - K))
     sum_CT += CT
     sum_CT2 += CT*CT
 next j
 
 call_value = sum_CT/M * exp(-r*T)
 SD = sqrt((sum_CT2 - sum_CT*sum_CT/M) * exp(-2*r*T)/(M-1))
 SE = SD/sqrt(M)
   

앞 글에서 설명했던 code와 달라진 점은, lnSt1, lnSt2의 초기 값이 달라졌다는 것과, 위에 설명된 수식을 대입한 것 뿐입니다.

각 parameter들을 넣어서 돌려보면 우리가 원하는 값들이 나오겠죠!