Hedging
Hedging : 환율, 금리 또는 다른 자산에 대한 투자 등을 통해 보유하고 있는 위험자산의 가격변동을 제거하는 것을 말한다.
즉, 확정되지 않은 자산을 확정된 자산으로 편입하는 과정이라 할 수 있으며, 주로 선물 옵션과 같은 파생상품을 이용한다. 이를 통해 체계적 위험을 제거할 수 있다.
이러한 Hedging의 과정은 크게 3단계로 나뉩니다.
1) option을 판다. (Selling the option)
2) 보험료를 은행에 넣는다. (Putting the premium in the bank)
3) 보유 주식의 균형을 조정한다. (Rebalancing the holding)
Hedging의 종류 중 두 가지를 오늘 살펴봅시다.
Delta Hedging
앞에서 언급했던 Pay-off와 Probability의 관계에서의 large spike를 떠올려 봅시다.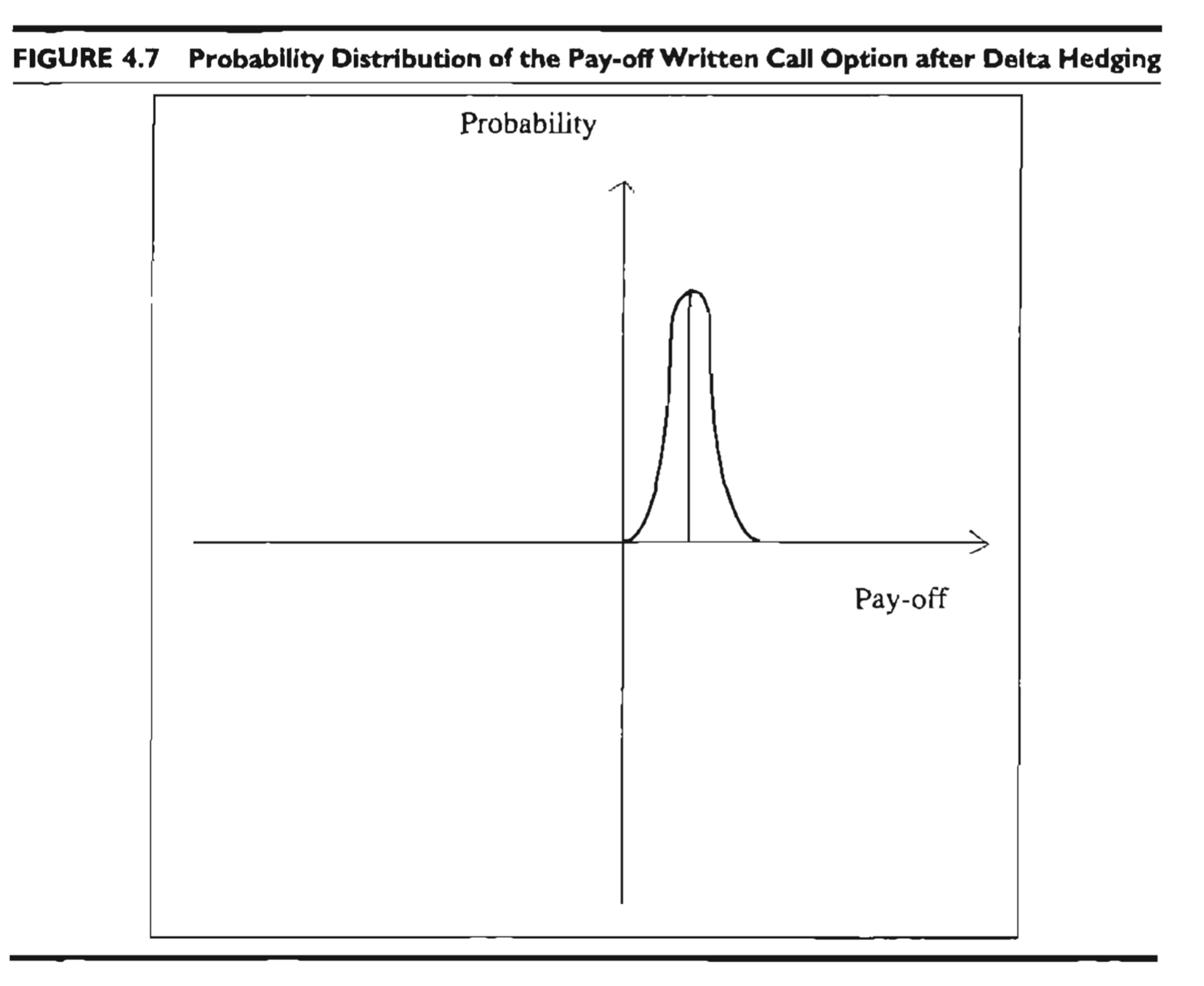
얘를 보아하니.. 미분방정식에서 봤던 Dirac-Delta function이 떠오르네요! 이 그래프는 그래서 바로.. 'delta hedging' 이후의 pay-off에 대한 확률 분포 그래프입니다.
앞에서부터 계속 얘기했다시피, hedging의 목표는 '안정성'입니다. 그럼 수학적으로 봤을 때, 이 option value의 변화를 얼마나 잘 상쇄시키느냐가 중요하겠죠?
그래서, delta hedging의 목표는 delta 값을 0으로 만드는 겁니다.
이 Hedge의 만기일에는 우리가 그 option에 대한 pay-off를 지불해야겠죠?
이것을 수식으로 나타내면,
이렇게 되는데요, 좀 어렵네요..;;
각 항의 의미를 알면 조금 이해가 쉬울 것 같은데요,
일단 첫번째 항 은 옵션 계약에 따른 보험료라고 보면 될 것 같아요. 그니까 초기값이라고 생각하면 편하겠죠?
두번째 항 은 각 날짜 의 hedging 균형을 맞추기 위한 돈의 흐름을 수식으로 나타냈다고 보면 될 것 같은데, 이 때 중요한 가정은 가 0의 값을 가진다는 거예요.
등호 오른쪽의 는 option에 대한 pay-off, 는 hedging error를 뜻합니다.
두번째 항 의 시그마 부분을 쭉 펼치고 잘 묶어보면,
이렇게 정리할 수 있습니다.
Delta hedging에서 우리는 Martingale-control-variate이라는 것을 알아야 되는데요, 이 때 Martingale 과정은 "과거의 모든 정보를 알고 있다면 미래의 기댓값이 현재 값과 동일한 과정" 입니다.
이 때, 위의 식에서 대괄호 내에 있는 부분이 Martingale-control-variate이 됩니다.
우리가 과거의 모든 정보를 알고 있다고 가정했으니, 이 녀석을 이라고 할게요! 그러면..
이니까, 의 평균(mean)은 0이 됨을 알 수 있어요. (이게 Delta Hedging의 정의!)
이렇게 control-variate 방법을 이용해서 우리는 분산을 줄이는 과정을 거쳤고, 아래 그래프를 보면 N이 커질수록 분산이 줄어드는 것을 볼 수 있습니다.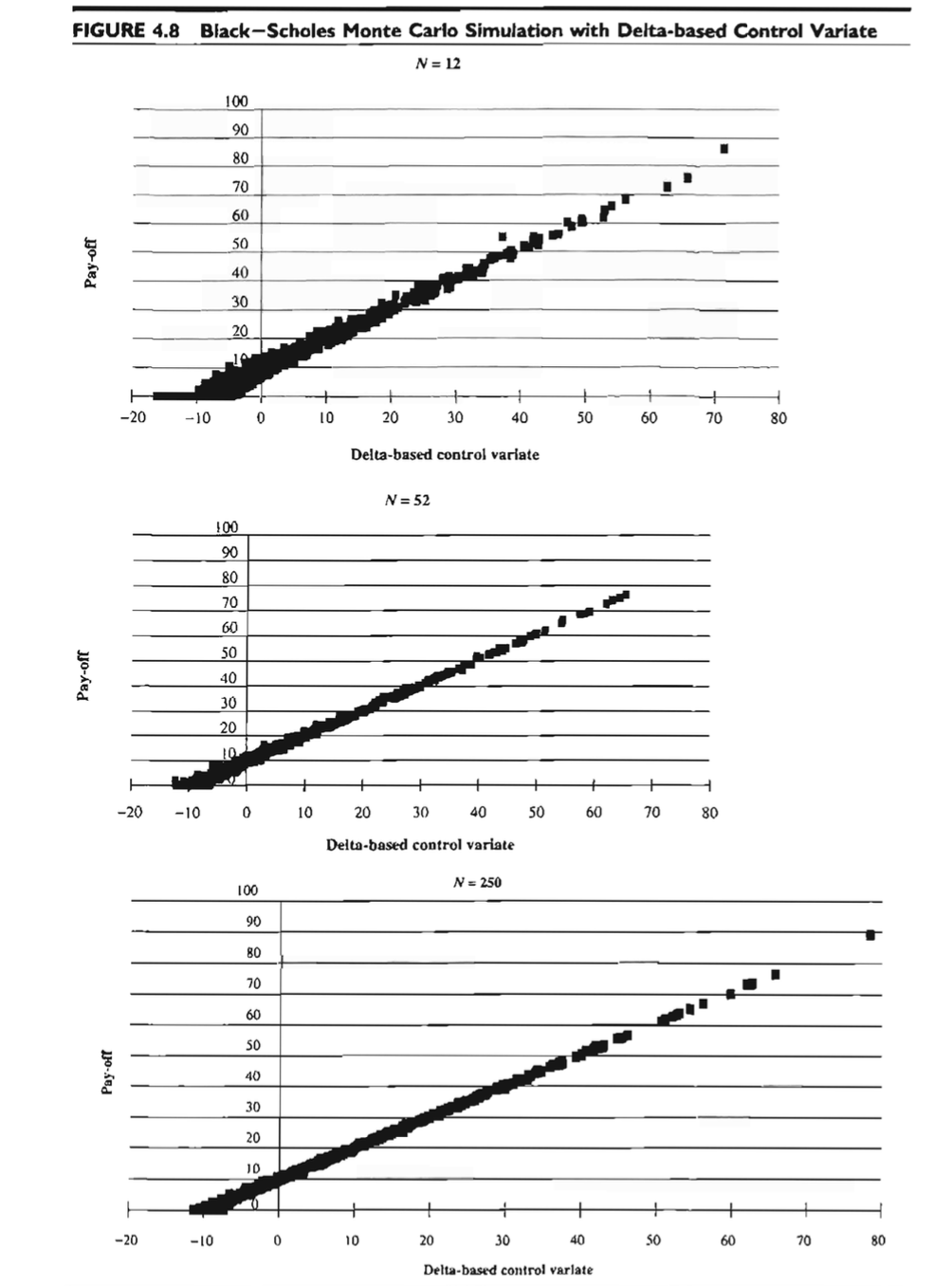
이렇게 Delta-Hedging을 알아보았는데요, control-variate를 좀 다르게 해서 다른 hedging 방법을 살펴볼게요.
Gamma Hedging
Gamma hedging에서의 control-variate를 라 해봅시다.
이렇게 정의된다네요.
수식으로 보니까 어려운데.. Gamma Hedging이 어떻게 하는 방법인가 하면,
시장이 생각하는 변동성 수준과 트레이더가 생각하는 변동성의 수준이 다를 때,
옵션 포지션을 구축한 후, 시간이 흐름에 따라 계속 기초자산을 사고 팔면서 전체 델타의 총합을 0으로 맞춰가는 매매기법입니다.
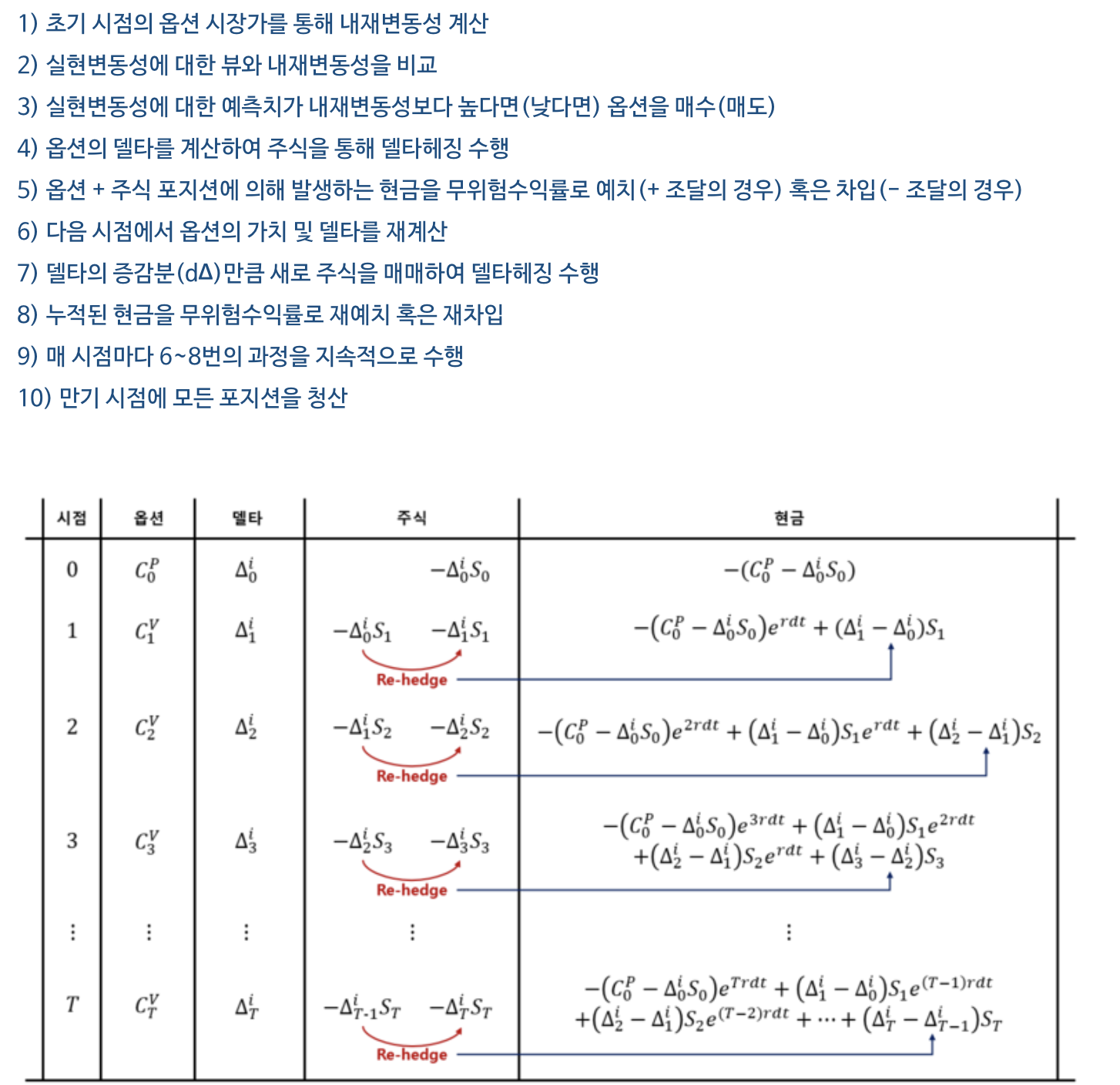
위의 사진을 보면 이해가 될 것 같네요.
General Case
위의 두 경우를 보셨다시피, Hedging은 일반적으로
로 표현됩니다.
이걸 그래프로 나타내면 당연히 Noise가 발생하겠죠? 우리가 이미 배운 Linear Regression을 사용해봅시다.
이고, 는 simulated pay-off의 벡터라고 합시다. 그러면..
요놈이 Linear regression을 통해 나오게 될 거예요!
이렇게 를 고정시키고, 다양한 예측 경로를 통한 hedged portfolio의 값의 평균을 구하면, option의 가격을 매길 수 있게 된다는 것이 말하고자 하는 바였습니다.
