누적 합(Prefix Sum, Cumulative Sum)
수열 An에 대해서, 구간 [1, 1]의 합, 구간 [1, 2]의 합, 구간 [1, 3]의 합, ..., [1, n]의 합을 누적 합이라고 한다.

하지만 이렇게 모든 입력마다 구간합을 일일히 구해주는 경우에는 구간의 길이가 M이라고 하면 매 구간합을 구할 때 마다 O(M)이라는 시간이 걸리게 됩니다. 즉, N개의 구간 에 대해 구간의 길이가 M인 구간합을 구하는 경우 O(N*M) = O(N²)의 시간 복잡도가 걸립니다.
기본적으로, 배열에서 특정 구간의 합을 직접 계산하는 경우에는 해당 구간의 길이(M)만큼의 연산이 필요합니다. 따라서, N개의 구간에 대해 합을 구하려면 O(NM)의 시간이 소요됩니다.
하지만 누적합 방법을 사용하면 이를 개선할 수 있습니다. 누적합은 배열의 처음부터 각 위치까지의 합을 미리 계산해 둔 것인데, 이를 O(N)의 시간에 계산할 수 있습니다. 이렇게 누적합을 만들어 두고 나면, 어떤 구간의 합도 두 개의 누적합 값만으로 O(1)의 시간에 구할 수 있습니다.
결국, 누적합을 활용하면 N개의 구간 합을 구하는데 필요한 전체 시간 복잡도는 누적합을 만드는 데 필요한 O(N)과 각 구간의 합을 구하는 데 필요한 O(N)을 합친 O(N + N) = O(2N)이며, 상수는 무시되므로 결국 O(N)이 됩니다.
이렇게 보면, 누적합을 이용하는 것이 배열에서 여러 구간의 합을 빠르게 구하는 데 매우 효율적임을 알 수 있습니다.
1차원 누적합을 구하는 방법은 다음과 같습니다.
- 먼저 원 배열의 0번째 인덱스부터 i번째 인덱스까지의 합을 누적합 배열의 i번째 위치에 저장합니다. 이때, 누적합 배열의 i번째 위치의 값은 원 배열의 i번째 값에 누적합 배열의 i-1번째 위치의 값을 더한 것입니다.
- 이렇게 하면, 누적합 배열의 x부터 y까지의 범위 합은 누적합 배열의 y 위치의 값에서 누적합 배열의 x-1 위치의 값을 빼면 됩니다
// 원 배열
int[] arr = {1, 2, 3, 4, 5};
// 누적합 배열
int[] prefixSum = new int[arr.length + 1];
// 누적합 계산
for (int i = 1; i <= arr.length; i++) {
prefixSum[i] = arr[i - 1] + prefixSum[i - 1];
}
// 1번째 인덱스부터 3번째 인덱스까지의 합
int x = 1, y = 3;
int sum = prefixSum[y] - prefixSum[x - 1];
위의 코드에서 1번째 인덱스부터 3번째 인덱스까지의 합은 2 + 3 + 4 = 9이며, 이 값은 sum에 저장됩니다.
이러한 문제를 개선하기 위해 누적 합을 이용하여 구간 합을 구하는 방법을 사용한다면, 시간 복잡도를 O(N + M) = O(N)까지 줄일 수 있습니다.
시간 복잡도
누적 합 알고리즘의 시간 복잡도는 두 부분으로 나뉩니다.
- 누적 합 계산: O(N) 2차원 배열 : O(N²)
배열의 모든 요소를 한 번씩 방문하며 누적 합을 계산하기 때문에 시간 복잡도는 O(N)입니다. 여기서 N은 배열의 길이를 나타냅니다. - 구간 합 계산: O(1)
누적 합을 사용하면 특정 구간의 합을 즉시 계산할 수 있습니다. 이 연산의 시간 복잡도는 O(1)입니다.
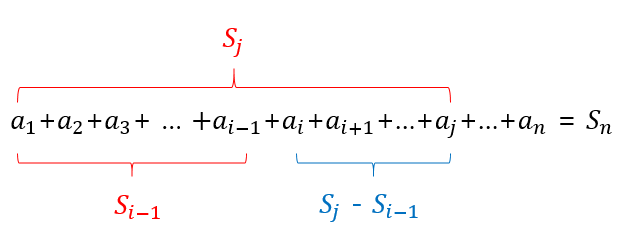
수열 An에서 구간 [i, j]까지의 구간 합을 구하는 경우구간 [i, j]의 구간합은 Sj와 Si-1을 뺀 값을 구하여 바로 구할 수 있습니다. 즉, Sn까지의 구간합을 모두 구해 놓기만 한다면(O(M)) 구간 합을 구하는 연산 자체는 O(1)의 시간이면 구할 수 있기 때문에 결론적으로 O(N + M) = O(N)의 시간 복잡도를 갖는 구간 합을 구하는 연산을 만들 수 있습니다.
1차원 배열
예를 들어, [1,2,4,8,9]의 배열이 있고, 0번째부터 3번째 원소까지 2만큼 빼야 하는 상황이라고 가정하겠습니다. 즉, 배열을 [-1,0,2,6,9]로 만들고 싶은 상황입니다. 가장 쉬운 방법으로는 0번째부터 3번째 원소까지 반복문을 사용해 2만큼 빼주는 방법이 있지만, 이 방법은 O(M)의 시간 복잡도가 걸립니다.
누적합을 이용한다면 O(M)의 시간 복잡도를 O(1)로 만들 수 있습니다. 위의 예시의 경우 [-2,0,0,0,2]를 저장한 새로운 배열을 생성합니다. 이 배열을 앞에서부터 누적합하면 [-2,-2,-2,-2,0]이 되기 때문에 초기 배열인 [1,2,4,8,9]과 더해주면 [-1,0,2,6,9]를 얻을 수 있게 됩니다. 즉, 1차원 배열의 i번째 원소부터 j번째 원소까지 c만큼의 변화를 주겠다고 하면 새로운 배열의 i번째 원소에 c를 더하고 j + 1번째 원소에 c를 빼면 됩니다.
public class RangeUpdate {
public static void main(String[] args) {
// 초기 배열
int[] arr = {1, 2, 4, 8, 9};
// 변화량을 기록할 배열
int[] diff = new int[arr.length + 1]; // 변화량 배열은 길이를 하나 더 크게 선언
// 구간 [0, 3]에 2만큼 빼기 (-2 적용)
int a = 0, b = 3, c = -2;
diff[a] += c; // a번째에 c를 더함
diff[b + 1] -= c; // b+1번째에 c를 뺌
// 누적합 계산
int[] result = new int[arr.length];
result[0] = arr[0] + diff[0];
for (int i = 1; i < arr.length; i++) {
diff[i] += diff[i - 1]; // 누적합 계산
result[i] = arr[i] + diff[i]; // 원본 배열에 더해 최종 배열 계산
}
// 결과 출력
for (int num : result) {
System.out.print(num + " ");
}
}
}
2차원 배열
2차원 누적합은 2차원 배열의 특정 범위 내의 합을 빠르게 구할 수 있습니다. 이를 통해, 일반적으로 O(N²)이 걸리는 작업을 O(1)에 해결할 수 있습니다.
2차원 누적합을 구하는 방법은 다음과 같습니다.
먼저 원 배열의 (0, 0)부터 (i, j)까지의 합을 누적합 배열의 (i, j) 위치에 저장합니다.
이를 위해, 누적합 배열의 (i, j) 위치에는 원 배열의 (i, j) 값에 누적합 배열의 (i-1, j), (i, j-1) 위치의 값들을 더하고, 중복으로 더해진 (i-1, j-1) 위치의 값을 빼줍니다.
이렇게 하면, 누적합 배열의 (x1, y1)부터 (x2, y2)까지의 범위 합은 누적합 배열의 (x2, y2) 값에서 (x1-1, y2), (x2, y1-1) 위치의 값들을 빼주고, 중복으로 빼진 (x1-1, y1-1) 위치의 값을 더해주면 됩니다.
위에서 설명한 방법을 코드로 나타내면 다음과 같습니다.
public class TwoDimensionalRangeUpdate {
public static void main(String[] args) {
// 초기 2차원 배열 (3x3 배열 예시)
int[][] arr = {
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
};
int n = arr.length; // 행 크기
int m = arr[0].length; // 열 크기
// 변화량을 기록할 2차원 배열 (diff 배열)
int[][] diff = new int[n + 1][m + 1];
// (1,1)부터 (2,2)까지 3만큼 더하기
int r1 = 1, c1 = 1, r2 = 2, c2 = 2, degree = 3;
diff[r1][c1] += degree; // (r1, c1)에 degree 더하기
diff[r1][c2 + 1] -= degree; // (r1, c2+1)에 degree 빼기
diff[r2 + 1][c1] -= degree; // (r2+1, c1)에 degree 빼기
diff[r2 + 1][c2 + 1] += degree;// (r2+1, c2+1)에 degree 더하기
// 행 방향으로 누적합 계산
for (int i = 0; i < n; i++) {
for (int j = 1; j < m; j++) {
diff[i][j] += diff[i][j - 1];
}
}
// 열 방향으로 누적합 계산
for (int j = 0; j < m; j++) {
for (int i = 1; i < n; i++) {
diff[i][j] += diff[i - 1][j];
}
}
// 원본 배열에 누적합 배열을 적용하여 최종 결과 계산
int[][] result = new int[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
result[i][j] = arr[i][j] + diff[i][j];
}
}
// 결과 출력
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
System.out.print(result[i][j] + " ");
}
System.out.println();
}
}
}
위의 코드에서 (1, 1)부터 (2, 2)까지의 범위 합은 5 + 6 + 8 + 9 = 28이며, 이 값은 sum에 저장됩니다.

