순열

a·2023년 9월 11일

알고리즘

목록 보기

9/17

순열 ( nPr )

순열이란 서로 다른 n개중에 r개를 선택하는 경우의 수를 의미합니다. (순서 상관 있음)

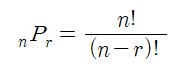
1. Swap 을 이용한 순열

첫번째는 swap 함수를 만들어서 배열들의 값을 직접 바꾸는 방법입니다.

배열의 첫 값부터 순서대로 하나씩 바꾸며 모든 값을 한번씩 swap 합니다.

depth 를 기준 인덱스로 하여 depth 보다 인덱스가 작은 값들은 그대로 고정하고

depth 보다 인덱스가 큰 값들만 가지고 다시 swap 을 진행합니다.

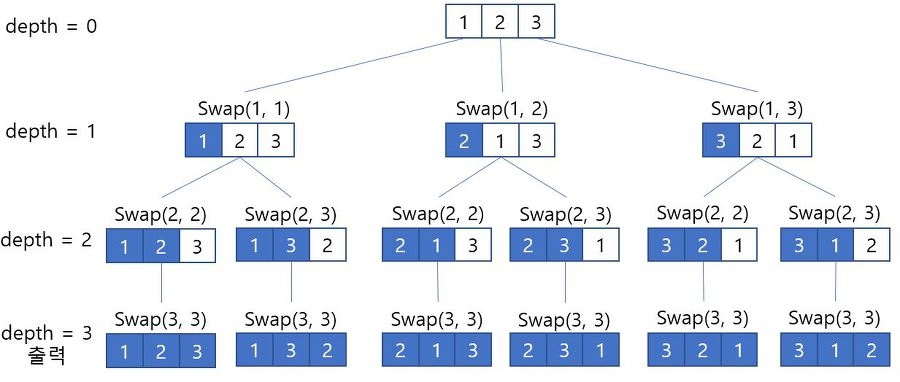
간단하고 코드도 깔끔하게 나오지만 순열들의 순서가 보장되지 않습니다.
예를 들어 3개의 숫자 중 3개의 값을 뽑는 순열을 만들 때

[3, 1, 2]
[3, 2, 1]

위 순서대로 나와야 하는데

[3, 2, 1]
[3, 1, 2]

이렇게 나옵니다.

Java Code

// 순서 없이 n 개중에서 r 개를 뽑는 경우
// 사용 예시: permutation(arr, 0, n, 4);
static void permutation(int[] arr, int depth, int n, int r) {
    if (depth == r) {
        print(arr, r);
        return;
    }
 
    for (int i=depth; i<n; i++) {
        swap(arr, depth, i);
        permutation(arr, depth + 1, n, r);
        swap(arr, depth, i);
    }
}
 
static void swap(int[] arr, int depth, int i) {
    int temp = arr[depth];
    arr[depth] = arr[i];
    arr[i] = temp;
}

Result

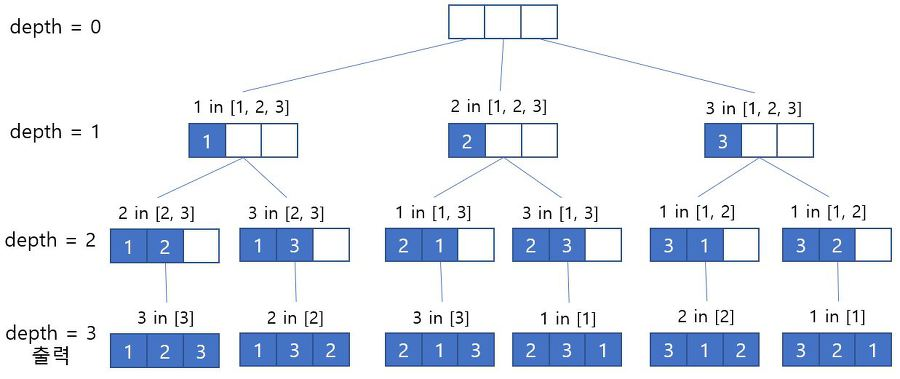
2. Visited 배열을 이용한 순열

두번째로는 visited 배열을 이용하는 방법입니다.

변수	설명
arr	r 개를 뽑기 위한 n 개의 값
output	뽑힌 r 개의 값
visited	중복해서 뽑지 않기 위해 체크하는 값

1번과 달리 사전식으로 순열을 구현할 수 있습니다.

위 3개의 값이 포인트입니다.

DFS를 돌면서 모든 인덱스를 방문하여 output 에 값을 넣습니다.

이미 들어간 값은 visited 값을 true 로 바꾸어 중복하여 넣지 않도록 합니다.

depth 값은 output 에 들어간 숫자의 길이라고 생각하시면 됩니다.

depth 의 값이 r 만큼 되면 output 에 들어있는 값을 출력하면 됩니다.

Java Code

public class Main {
    static void perm(int[] arr, int[] output, boolean[] visited, int depth, int n, int r) {
        // depth가 r이면 현재 output 배열 출력
        if (depth == r) {
            return;
        }
        
        // 각 인덱스를 방문하며 순열을 생성
        for (int i = 0; i < n; i++) {
            if (!visited[i]) {          // 아직 방문하지 않은 원소 선택
                visited[i] = true;      // 방문 처리
                output[depth] = arr[i]; // 선택한 원소 저장
                perm(arr, output, visited, depth + 1, n, r);  // 재귀 호출
                visited[i] = false;     // 백트래킹: 방문 해제
                // list일 경우 마지막 원소 제거 (백트래킹)추가
            }
        }
    }
    
    public static void main(String[] args) {
        int[] arr = {1, 2, 3, 4, 5};
        int[] output = new int[arr.length];
        boolean[] visited = new boolean[arr.length];
        int n = arr.length;
        int r = 3; // r개의 원소로 이루어진 순열
        
        perm(arr, output, visited, 0, n, r);
    }
}

output이 list일 경우

import java.util.*;

public class Main {
    // 순열 결과를 저장할 리스트를 인스턴스 변수로 선언하거나, 
    // 메서드 인자로 List<List<Integer>>를 추가하여 최종 결과를 모을 수 있습니다.
    // 여기서는 최종 결과를 모으는 List<List<Integer>>를 사용합니다.
    static List<List<Integer>> results = new ArrayList<>();
    
    // perm 메서드 시그니처 변경: output 배열 대신 List<Integer> currentPermutation 사용
    static void perm(int[] arr, List<Integer> currentPermutation, boolean[] visited, int depth, int n, int r) {
        
        // depth가 r이면 현재 순열이 완성됨
        if (depth == r) {
            // 깊은 복사(Deep Copy): 현재 순열 리스트를 복사하여 최종 결과 리스트에 추가
            results.add(new ArrayList<>(currentPermutation));
            return;
        }
        
        // 각 인덱스를 방문하며 순열을 생성
        for (int i = 0; i < n; i++) {
            if (!visited[i]) {                      // 아직 방문하지 않은 원소 선택
                visited[i] = true;                  // 방문 처리
                currentPermutation.add(arr[i]);     // **List에 선택한 원소 추가**

                perm(arr, currentPermutation, visited, depth + 1, n, r);  // 재귀 호출
                
                // -------- 백트래킹 영역 --------
                // 1. **List에서 마지막에 추가했던 원소를 제거**
                // (List의 크기가 줄어들면서 메모리에서 해당 원소가 논리적으로 삭제됨)
                currentPermutation.remove(currentPermutation.size() - 1);
                
                // 2. 방문 해제
                visited[i] = false;     
            }
        }
    }
    
    public static void main(String[] args) {
        int[] arr = {1, 2, 3, 4, 5};
        
        // List를 output 대신 현재 순열을 저장하는 임시 공간으로 사용
        List<Integer> currentPermutation = new ArrayList<>(); 
        
        boolean[] visited = new boolean[arr.length];
        int n = arr.length;
        int r = 3; // r개의 원소로 이루어진 순열
        
        perm(arr, currentPermutation, visited, 0, n, r);

        System.out.println("생성된 순열 (r=" + r + "): " + results);
    }
}

Result

배열: 고정된 크기의 공간에 덮어쓰기 하므로 마지막 값을 제거할 필요 없음.
리스트: 원소를 끝에 추가하므로 백트래킹 시 마지막에 추가된 값을 제거해야 함.

백트래킹

백트래킹을 사용하여 순열을 생성할 때, 각 원소의 선택 상태를 기록하기 위해 visited[] 배열을 사용할 수 있습니다. 이 배열은 특정 원소가 현재 선택되었는지를 나타내며, 선택된 원소가 있으면 다른 원소를 선택하지 않도록 합니다. 아래에 visited[]를 포함한 백트래킹을 통해 순열을 생성하는 과정을 보여드립니다.

백트래킹(Backtracking)은 모든 가능한 경우를 탐색하면서, 불필요한 경로를 미리 차단하는 알고리즘 기법입니다. 가능한 모든 선택지를 탐색하되, 그 선택이 유효하지 않으면 되돌아가는 방식으로 문제를 해결합니다. 이를 통해 비효율적인 경로를 최소화하고, 가능한 최적의 해를 찾습니다.

순열 예시:

여기서 예를 들어 [1, 2, 3]으로 순열을 구한다고 가정합니다.

시작: 빈 리스트 []에서 시작합니다.
1을 선택: [1]로 선택합니다. 이제 나머지 원소인 [2, 3]을 선택할 차례입니다.
2를 선택: [1, 2]로 선택합니다. 이제 남은 원소 [3]을 선택할 차례입니다.
3을 선택: [1, 2, 3] 완성되었습니다. 이 순열을 저장합니다.
백트래킹 시작: 마지막 선택한 3을 제거하고 [1, 2]로 돌아갑니다.
2를 제거: [1]으로 돌아가고, 다른 선택지인 3을 선택합니다.
3을 선택: [1, 3]으로 선택 후, 남은 [2]를 선택합니다.
2 선택: [1, 3, 2] 순열이 완성되어 저장합니다.
다시 백트래킹: 선택한 2를 제거하고, [1, 3]에서 3도 제거하여 다시 [1]로 돌아갑니다.
이 과정을 반복: [2], [3]로 시작하는 선택지들도 위와 같은 방식으로 탐색합니다.

핵심은:

선택지 탐색: 가능한 모든 경우를 시도하고,
유효성 검사: 현재 상태가 조건을 만족하는지 확인하고,
백트래킹: 선택이 실패하거나 다른 경로를 탐색하기 위해 다시 되돌아가는 과정입니다.

흐름도

아래는 visited[]를 포함한 백트래킹을 통한 순열 생성 과정을 요약한 흐름도입니다:

1. 시작: []
   visited: [false, false, false]
   |
   ├─ 1을 선택: [1]
   │   visited: [true, false, false]
   │   ├─ 2를 선택: [1, 2]
   │   │   visited: [true, true, false]
   │   │   └─ 3을 선택: [1, 2, 3] -> 저장
   │   └─ 3을 선택: [1, 3]
   │       visited: [true, false, true]
   │       └─ 2를 선택: [1, 3, 2] -> 저장
   ├─ 2를 선택: [2]
   │   visited: [false, true, false]
   │   ├─ 1을 선택: [2, 1]
   │   │   visited: [true, true, false]
   │   │   └─ 3을 선택: [2, 1, 3] -> 저장
   │   └─ 3을 선택: [2, 3]
   │       visited: [false, true, true]
   │       └─ 1을 선택: [2, 3, 1] -> 저장
   └─ 3을 선택: [3]
       visited: [false, false, true]
       ├─ 1을 선택: [3, 1]
       │   visited: [true, false, true]
       │   └─ 2를 선택: [3, 1, 2] -> 저장
       └─ 2를 선택: [3, 2]
           visited: [false, true, true]
           └─ 1을 선택: [3, 2, 1] -> 저장

중복 순열

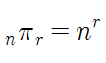
서로 다른 n개에서 중복이 가능하게 r개를 뽑아서 정렬하는 경우의 수입니다.

순서가 있게 뽑는 순열과 동일하지만, 같은 원소를 중복해서 뽑을 수 있다는 차이만 있습니다.
순열과 유일한 차이가 중복이 가능하다는 것이므로, 순열 코드에서 중복을 방지하기 위해서 사용했던 visited부분을 제거해주면 됩니다.

Java Code

import java.util.ArrayList;
import java.util.List;

public class PermutationWithRepetition {
    public static void main(String[] args) {
        String[] elements = {"A", "B"};
        int r = 2; // 선택할 개수
        List<String> results = new ArrayList<>();
        
        // 중복 순열 생성
        generatePermutations(elements, r, "", results);
    }

    private static void generatePermutations(String[] elements, int r, String current, List<String> results) {
        if (current.length() == r) {
            results.add(current);
            return;
        }
        
        // for 문을 사용하여 중복 순열 생성
        for (int i = 0; i < elements.length; i++) {
            generatePermutations(elements, r, current + elements[i], results);
        }
    }
}

조합(nCr)

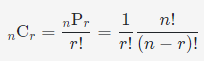
nCr = n-1Cr-1 + n-1Cr
하나의 원소를 선택할 경우 + 하나의 원소를 선택하지 않을 경우

조합은 n개 중 서로 다른 r개를 선택하되 순서를 고려하지 않는 경우의 수를 말합니다.
순서를 고려해서 뽑는 순열에서 중복을 제거해준 형태입니다.

재귀를 할용한 조합 개수

public class Main {
    public static int combination(int n, int r) {
        if (n == r || r == 0)
            return 1;
        else
            return combination(n - 1, r - 1) + combination(n - 1, r);
    }

    public static void main(String[] args) {
        System.out.println(combination(5, 3));  // 5C3를 계산
    }
}

조합

public class Main {
    static int[] arr;
    static List<Integer> output;
    static Set<List<Integer>> combinations = new HashSet<>(); // 조합을 저장할 리스트
    
    public static void combination(int start, int depth, int r) {
        // depth가 r이면 현재 output 배열을 리스트에 추가
        if (depth == r) {
        	combinations.add(new ArrayList<>(output)); // 현재 조합을 리스트에 추가
            return;
        }

        for (int i = start; i < arr.length; i++) {
             output.add(arr[i]); // 선택한 원소 저장
            combination(i + 1, depth + 1, r); // 재귀 호출
            output.remove(output.size() - 1); // 마지막 원소 제거 (백트래킹)
        }
    }

    public static void main(String[] args) {
        arr = new int[]{1, 2, 3, 4, 5};
        output = new ArrayList<>();
        int r = 3; // r개의 원소로 이루어진 조합
        
        combination(0, 0, r);
    }
}

start 인수 역할

중복 방지: start 인수를 통해 이미 선택된 원소를 다시 선택하지 않도록 합니다. 예를 들어, 선택된 원소가 1, 2, 3일 때, 다음으로 선택할 수 있는 원소는 4와 5만 있게 됩니다. 이렇게 하면 조합의 중복을 방지할 수 있습니다.

순서 제어: start 인수를 사용하면 조합을 생성할 때 선택할 수 있는 인덱스의 범위를 제한할 수 있습니다. 이는 조합이 항상 오름차순으로 정렬되도록 보장합니다.

재귀 호출에서의 진행: 재귀 호출 시, start 값을 증가시켜 다음 호출에서 선택할 수 있는 인덱스를 조정합니다. 이를 통해 각 호출 단계에서 다른 원소를 선택할 수 있습니다.

start 인수를 사용할 때와 안 할 때의 구별은 조합을 구하는 방식과 문제의 요구사항에 따라 달라집니다. 두 가지 경우를 나누어 설명하겠습니다.

1. `start` 인수가 필요한 경우

start 인수는 조합(combination)에서 주로 사용됩니다. 조합을 구할 때는 순서가 중요하지 않고, 중복 선택을 방지해야 하기 때문에, 이전에 선택된 원소 이후의 원소만을 선택할 수 있도록 start 인수를 사용하여 범위를 제한합니다.

사용해야 하는 경우:

동일한 리스트에서 중복되지 않은 원소를 여러 번 선택할 때.
순서를 고려하지 않고 중복 없이 원소를 조합할 때.

예시: 숫자 리스트에서 조합 구하기

public void combination(int[] arr, List<Integer> output, int start, int depth, int r) {
    if (depth == r) {
        System.out.println(output);
        return;
    }
    for (int i = start; i < arr.length; i++) {
        output.add(arr[i]);
        combination(arr, output, i + 1, depth + 1, r); // i+1로 시작 인덱스 업데이트
        output.remove(output.size() - 1); // 백트래킹
    }
}

이 코드에서는 start 인수를 통해 선택된 원소의 다음 원소부터 선택을 하도록 하고, 이를 통해 중복된 원소 선택을 방지합니다. 예를 들어 [1, 2, 3]에서 2개를 선택하는 경우, (1, 2)와 (2, 1)은 같은 조합이므로 중복을 피하기 위해 start 인수를 사용합니다.

2. `start` 인수가 필요하지 않은 경우

start 인수가 필요하지 않은 경우는 리스트가 각각 독립적이거나, 순서가 상관없는 경우입니다. 이때는 원소를 중복해서 선택할 필요가 없으며, 다른 조건을 통해 중복을 방지하는 방식으로 문제를 해결할 수 있습니다.

사용하지 않아도 되는 경우:

각 단계에서 선택하는 리스트가 서로 독립적일 때.
조합이 아닌, 단순히 모든 경우의 수를 탐색할 때.

예시: 여러 리스트에서 매칭 조합 구하기 (이 문제와 유사한 경우)

public void dfs(int depth, List<List<String>> matchesList, Set<String> selected) {
    if (depth == matchesList.size()) {
        System.out.println(selected);
        return;
    }
    for (String user : matchesList.get(depth)) {
        if (!selected.contains(user)) {
            selected.add(user);
            dfs(depth + 1, matchesList, selected);
            selected.remove(user); // 백트래킹
        }
    }
}

이 코드에서는 각 리스트가 독립적으로 존재하기 때문에, start 인수를 사용하지 않고도 중복 선택을 방지할 수 있습니다. 리스트의 각 단계에서 이미 선택된 사용자를 관리하는 Set을 통해 중복 선택을 방지하고, 다음 단계로 넘어가게 됩니다.

`start` 인수를 사용해야 하는 경우 vs 사용하지 않아도 되는 경우 요약

같은 리스트에서 여러 개를 선택하고 중복 선택을 방지하고 싶다면, start 인수를 사용합니다. (예: 배열에서 조합 구하기)
각 단계의 리스트가 독립적이거나, 선택된 원소만 중복되지 않으면 되는 경우라면, start 인수 없이 단순히 중복 관리(set이나 flag)를 통해 해결할 수 있습니다. (예: 이 문제처럼, banned_id와 user_id 간의 매칭)

간단한 판별 기준:

동일 리스트에서 여러 원소를 순서 없이 중복 없이 선택해야 한다면 start 인수를 사용.
독립적인 리스트나 각각 다른 조건에서 원소를 선택한다면, start 인수가 필요하지 않고, 다른 방법으로 중복만 처리하면 충분.

중복 조합

import java.util.*;

public class CombinationWithRepetition {
    public static void main(String[] args) {
        String[] elements = {"A", "B"};
        int r = 2; // 선택할 개수
        List<String> results = new ArrayList<>();
        generateCombinations(elements, r, 0, "", results);
    }

    private static void generateCombinations(String[] elements, int r, int start, String current, List<String> results) {
        if (current.length() == r) {
            results.add(current);
            return;
        }
        for (int i = start; i < elements.length; i++) {
            generateCombinations(elements, r, i, current + elements[i], results);
        }
    }
}

조합: 같은 요소는 한 번만 선택할 수 있습니다 (i + 1)
중복 조합: 같은 요소를 여러 번 선택할 수 있습니다 (i)

출처
https://bcp0109.tistory.com/14
https://coding-factory.tistory.com/606

순열

알고리즘

순열 ( nPr )

1. Swap 을 이용한 순열

Java Code

Result

2. Visited 배열을 이용한 순열

Java Code

output이 list일 경우

Result

백트래킹

순열 예시:

중복 순열

Java Code

조합(nCr)

재귀를 할용한 조합 개수

조합

start 인수 역할

1. `start` 인수가 필요한 경우

사용해야 하는 경우:

예시: 숫자 리스트에서 조합 구하기

2. `start` 인수가 필요하지 않은 경우

사용하지 않아도 되는 경우:

예시: 여러 리스트에서 매칭 조합 구하기 (이 문제와 유사한 경우)

`start` 인수를 사용해야 하는 경우 vs 사용하지 않아도 되는 경우 요약

간단한 판별 기준:

중복 조합

다익스트라/데이크스트라 알고리즘

누적 합(Prefix Sum , Cumulative Sum)

0개의 댓글

순열

알고리즘

순열 ( nPr )

1. Swap 을 이용한 순열

Java Code

Result

2. Visited 배열을 이용한 순열

Java Code

output이 list일 경우

Result

백트래킹

순열 예시:

중복 순열

Java Code

조합(nCr)

재귀를 할용한 조합 개수

조합

start 인수 역할

1. start 인수가 필요한 경우

사용해야 하는 경우:

예시: 숫자 리스트에서 조합 구하기

2. start 인수가 필요하지 않은 경우

사용하지 않아도 되는 경우:

예시: 여러 리스트에서 매칭 조합 구하기 (이 문제와 유사한 경우)

start 인수를 사용해야 하는 경우 vs 사용하지 않아도 되는 경우 요약

간단한 판별 기준:

중복 조합

다익스트라/데이크스트라 알고리즘

누적 합(Prefix Sum , Cumulative Sum)

0개의 댓글

1. `start` 인수가 필요한 경우

2. `start` 인수가 필요하지 않은 경우

`start` 인수를 사용해야 하는 경우 vs 사용하지 않아도 되는 경우 요약