Chapter 1. Linear Regression : 선형 회귀

선형 회귀 이해

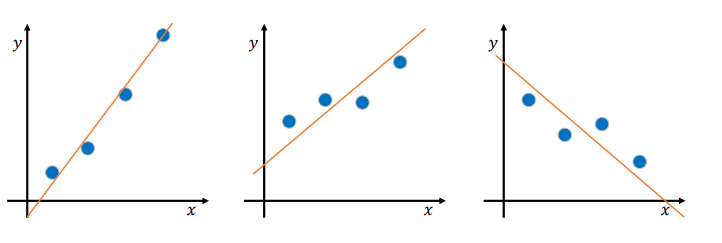
• 데이터는 다양한 형태를 가질 것이며 최선의 직선을 긋기가 쉽지 않음
• 과연 위 직선이 가장 최선의 직선일 것인가?
• 함수 𝑦 = 𝑎𝑥 + 𝑏 에서 최선의 기울기 𝑎와 𝑦 절편 𝑏를 결정하는 방법이 필요
• 이것이 선형 회귀이며, 직선을 회귀선이라고 부름
• 회귀 모델에만 사용

기호

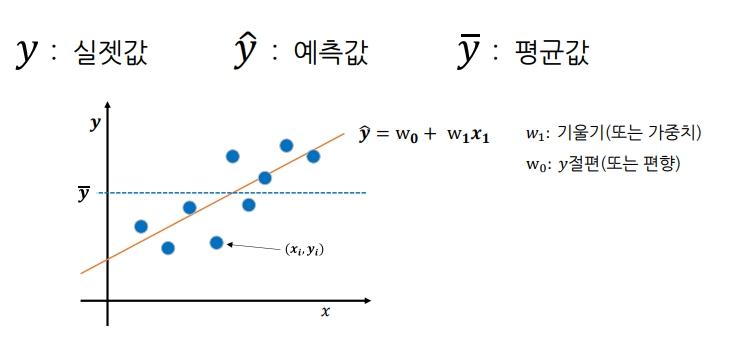
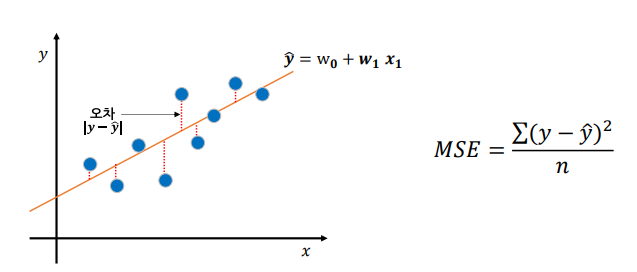
최적의 회귀 모델

• 최선의 회귀 모델은 전체 데이터의 오차 합이 최소가 되는 모델
• 오차 합이 최소가 되는 가중치 $w_1$와 편향 $w_0$을 찾는 것

---

단순 회귀(Simple Regression)

독립 변수의 개수로 회귀 분석을 단순회귀 와 다중 회기로 분류

• 독립변수 하나가 종속변수에 영향을 미치는 선형 회귀
• 𝑥 값 하나만으로 𝑦값을 설명할 수 있는 경우
  • ex) 행복지수(종속변수) 가 연수입(독립변수) 만으로 결정 됨
• 회귀식 : $\hat{y} = w_0 + w_1 x_1$
• 독립 변수의 최선의가중치 $w_1$와 편향 $w_0$을 찾음

단순 회귀의 회귀 계수

• 모델 학습 후 회귀 계수 확인 가능
• coef_ : 회귀 계수 (가중치)
• intercept_ : 편향

# 회귀계수 확인
print(model.coef_)
print(model.intercept_)

$𝑦 = −15.81 + 3.92 ∙ 𝑥$

---

다중 회귀 (Multiple Regression)

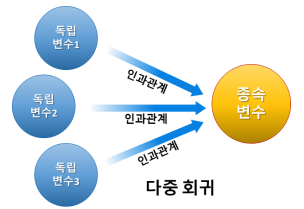
• 여러 독립변수가 종속변수에 영향을 미치는 선형 회귀
• 𝑦 값을 설명하기 위해서는 여러 개의 𝑥 값이 필요한 경우
  • ex) 여러 요인들(독립변수들)에 의해 보스턴 지역 집 값(종속변수) 이 결정 됨
• $\hat{y} = w0 + w1𝑥1 + w2𝑥2 + w3𝑥3 + ⋯ + w𝑛𝑥_n$
• 각 독립변수의 최선의 가중치와(w1, w2, w3, w4…)와 편향(w0)을 찾음

다중 회귀의 회귀 계수

• 회귀 계수가 여럿이므로 독립변수 이름과 같이 확인하기를 권고

# 회귀계수 확인
print(list(x_train))
print(model.coef_)
print(model.intercept_)

$𝑂𝑧𝑜𝑛𝑒 = −53.37 + 1.52 ∙ 𝑇𝑒𝑚𝑝 − 3.57 ∙ 𝑊𝑖𝑛𝑑 + 0.07 ∙ 𝑆𝑜𝑙𝑎𝑟. R$

---

단순 회귀 실습 : Cars

데이터

모델링

# 1단계: 불러오기
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, r2_score 

# 2단계: 선언하기
model = LinearRegression()

# 3단계: 학습하기
model.fit(x_train, y_train)

# 4단계: 예측하기
y_pred = model.predict(x_test)

# 5단계: 평가하기
print('MAE:',mean_absolute_error(y_test, y_pred).round(4))
print('R2:',r2_score(y_test, y_pred).round(4))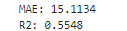

회귀 계수 확인

# 회귀계수 확인
print('* 가중치:', model.coef_)
print('* 편향:', model.intercept_)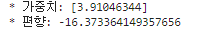

회귀식

$Distance = 3.91\times speed - 16.37$

시각화

# 시각화
plt.plot(y_test.values, label='Actual')
plt.plot(y_pred, label='Predicted')
plt.legend()
plt.ylabel('Dist(ft)')
plt.show()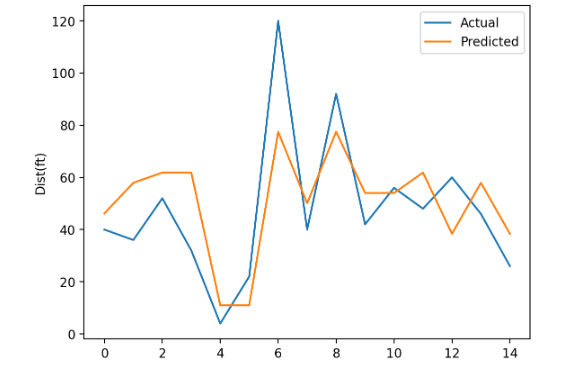

# dist = a * speed + b

a = model.coef_
b = model.intercept_
speed = np.array([x_train.min(), x_train.max()])
dist = a*speed + b

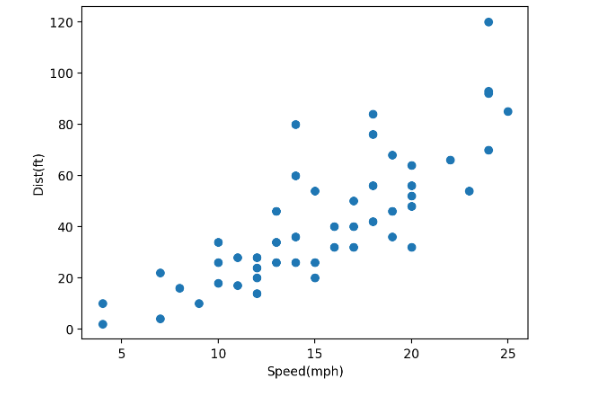
# 학습 데이터
# speed, dist 관계
plt.scatter(x=x_train['speed'], y=y_train) #학습 데이터
plt.scatter(x=x_test['speed'], y=y_test) #평가 데이터
plt.plot(speed,dist, color='r')
plt.axhline(y_train.mean(), linestyle='--') #학습 데이터 평균 선
plt.xlabel('Speed(mph)')
plt.ylabel('Dist(ft)')
plt.show()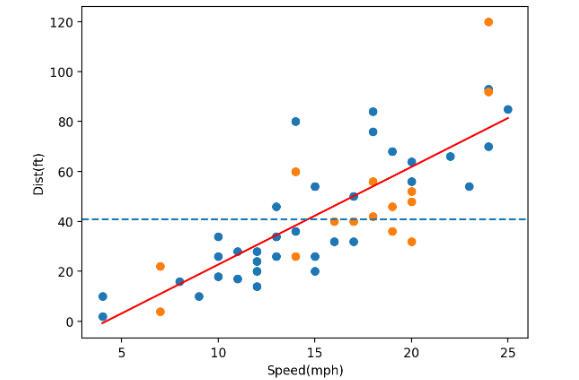

노란색 점이 평가 데이터

---

다중 회귀 실습 : Carseat

• 데이터
  

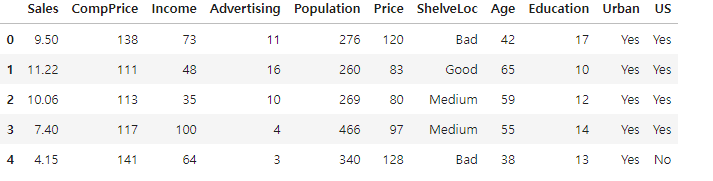
• 데이터 전처리 x 가변수화
  

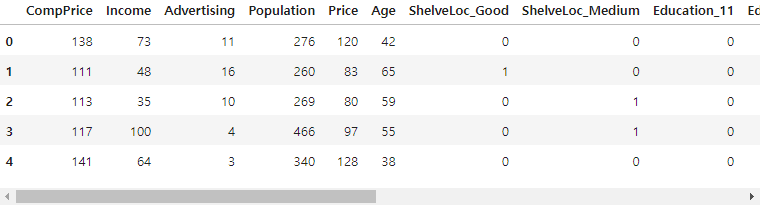
모델링

# 1단계: 불러오기
# 2단계: 선언하기
# 3단계: 학습하기
# 4단계: 예측하기
# 5단계: 평가하기
print('MAE:',mean_absolute_error(y_test, y_pred).round(4))
print('R2:',r2_score(y_test, y_pred).round(4))

회귀 계수 확인

# 회귀계수 확인
print(list(x_train))
print('* 가중치:', model.coef_.round(2))
print('* 편향:', model.intercept_.round(2))

회귀식

$Sales = 0.09 \times CompPrice + 0.01 \times Advertising + ... - 0.24 \times US\_Yes + 6.1$

시각화

# 가중치 시각화
tmp = pd.DataFrame()
tmp['feature'] = list(x)
tmp['weight'] = model.coef_
tmp.sort_values(by='weight',ascending=True,inplace=True)

#가로 막대
plt.figure(figsize=(3,5))
plt.barh(tmp['feature'],tmp['weight'])
plt.show()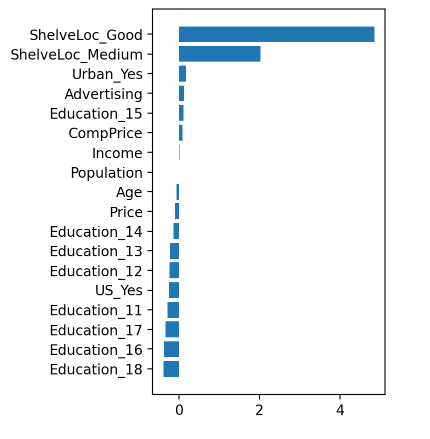

# 예측값, 실젯값 시각화
plt.figure(figsize=(12,3))
plt.plot(y_test.values, label='Actual', linewidth=0.7, marker='o', markersize=1)
plt.plot(y_pred, label='Predicted' , linewidth=0.7, marker='o', markersize=1)
plt.legend()
plt.ylabel('Sales')
plt.show()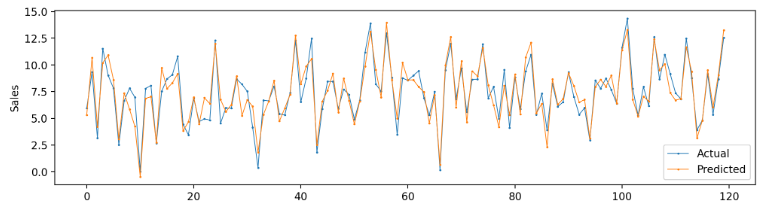

---

---

Chapter 2. K-Nearest Neighbor

KNN

• k-Nearest Neighbor: k 최근접 이웃(가장 가까운 이웃 k개)
• 학습용 데이터에서 k개의 최근접 이웃의 값을 찾아 그 값들로 새로운 값을 예측하는 알고리즘
• 회귀와 분류에 사용되는 매우 간단한 지도학습 알고리즘
• 다른 알고리즘에 비해 이해하기 쉽지만, 연산 속도가 느림

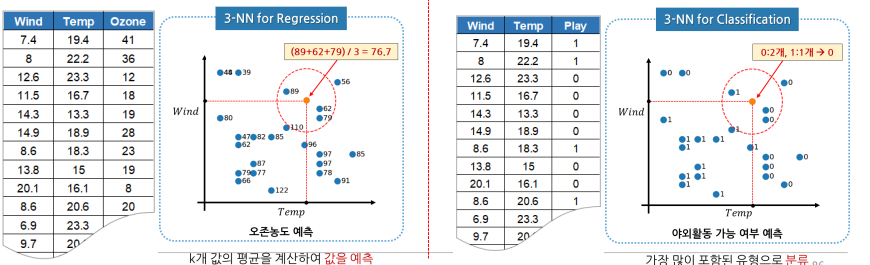
K의 중요성

• k k(탐색하는 이웃 개수)에 따라 데이터를 다르게 예측할 수도 있음
• k 값에 따라 예측 값이 달라지므로 적절한 k 값을 찾는 것이 중요(기본값=5)
• 일반적으로
  • k를 1로 설정 안함 → 이웃 하나로 현재 데이터를 판단하기에는 너무 편향된 정보
  • k를 홀수로 설정 → 짝수인 경우 과반수 이상의 이웃이 나오지 않을 수 있음
• 검증 데이터로 가장 정확도가 높은 k를 찾아 KNN 알고리즘의 k로 사용

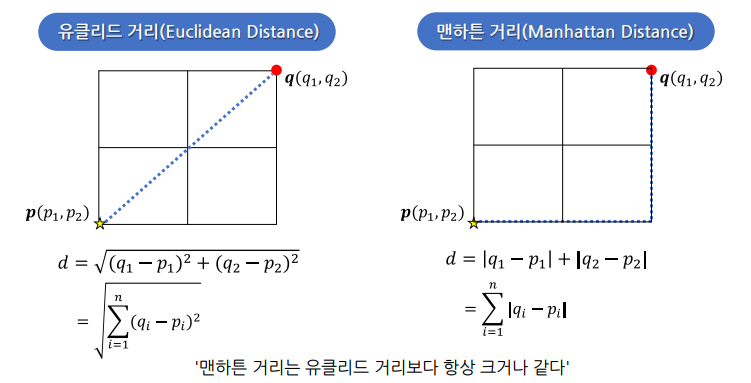
거리 구하기

---

스케일링

• 스케일링 여부에 따라 KNN 모델 성능이 달라질 수 있음을 꼭 기억해야 함

대표적 스케일링 방법

• 평가용 데이터에도 학습용 데이터를 기준으로 스케일링을 수행함(학습용 데이터의 최댓값, 최솟값, 평균 등을 사용)
• 위 공식을 직접 사용하거나, 다음과 같이 sklearn이 제공하는 함수를 사용해도 됨

# 함수 불러오기
from sklearn.preprocessing import MinMaxScaler
# 정규화
scaler = MinMaxScaler()
scaler.fit(x_train)
x_train = scaler.transform(x_train)
x_test = scaler.transform(x_test)

---

KNN 실습 : AirQuality

• 데이터
  
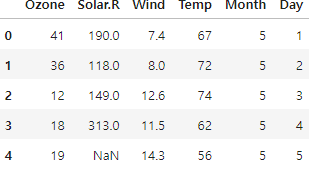
• 결측치 선형 보강법으로 채우기

# 결측치 채우기(선형 보강법)
data.interpolate(method='linear', inplace=True)

• Month, Day 변수 제거
• 데이터 분리

정규화

• 정규화 전 => 정규활르 통해 동일한 스케일로 변환

plt.figure(figsize=(6,3))
plt.boxplot(x_train, vert=False, labels=list(x))
plt.show()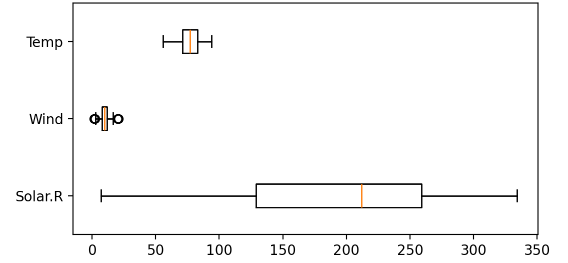

• 방법 1 : 공식 사용

# 최댓값, 최솟값 구하기
x_min = x_train.min()
x_max = x_train.min()


# 정규화
x_train = (x_train - x_min) / (x_max - x_min)
x_test = (x_test - x_min) / (x_max - x_min)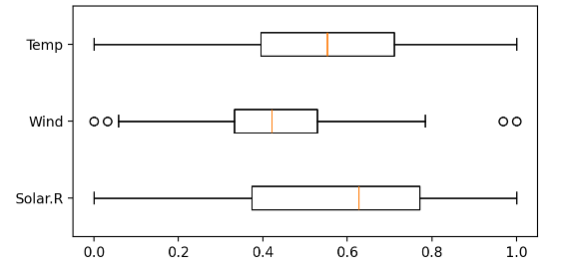

• 방법 2 : 함수 사용

# 모듈 불러오기
from sklearn.preprocessing import MinMaxScaler

# 정규화
scaler = MinMaxScaler()
x_train = scaler.fit_transform(x_train)
x_test = scaler.transform(x_test)

x_train

MinMaxScaler()를 사용하면, 데이터프레임이 아닌 np array가 되기때문에 무엇이 어떤 값인지 알 수 없다. => 더이상 데이터를 분석해 볼 수 없다.

---

---

Chapter 3. Decision Tree

• 질문을 해서 분류해가는 것
• 특정 변수에 대한 의사결정 규칙을 나무 가지가 뻗는 형태로 분류해 나감
• 분류와 회귀 모두에 사용되는 지도학습 알고리즘
• 스케일링 등의 전처리 영향도가 크지 않음
• 분석 과정이 직관적
• 분석 과정을 실제로 눈으로 확인할 수 있음 → 화이트박스 모델
• 의미 있는 질문을 먼저 하는 것이 중요
• 훈련 데이터에 대한 제약 사항이 거의 없는 유연한 모델
  -> 과적합으로 모델 성능이 떨어지기 쉬움
  -> 트리 깊이를 제한하는(=가지치기) 튜닝이 필요

---

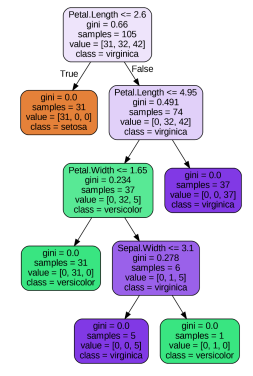
용어

• Root Node(뿌리 마디): 전체 자료를 갖는 시작하는 마디
• Child Node(자식 마디): 마디 하나로부터 분리된 2개 이상의 마디
• Parent Node(부모 마디): 주어진 마디의 상위 마디
• Terminal Node(끝 마디): 자식 마디가 없는 마디(=Leaf Node)
• Internal Node(중간 마디): 부모 마디와 자식 마디가 모두 있는 마디
• Branch(가지): 연결되어 있는 2개 이상의 마디 집합
• Depth(깊이): 뿌리 마디로부터 끝 마디까지 연결된 마디 개수(오른쪽 트리의 경우 5)

---

분류와 회귀

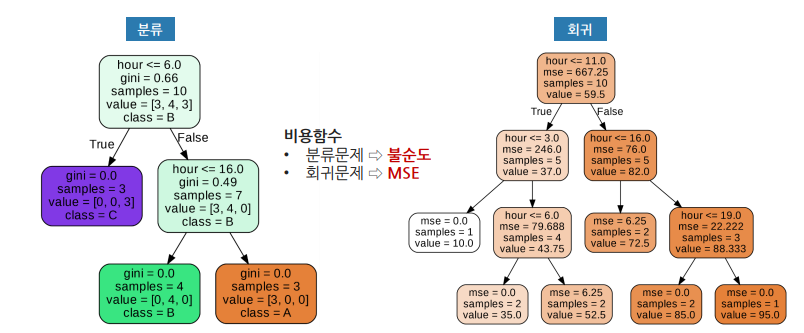
• 분류 : 마지막 노드에 있는 샘플들의 최빈값을 예측값으로 반환.
• 회귀 : 마지막 노드에 있는 샘플들의 평균을 예측값으로 반환

---

불순도(Impurity)

• 불순도가 낮을 수록 분류가 잘 된 것
• 불순도를 수치화 할 수 있는 지표
  • 지니 불순도
  • 엔트로피

지니 불순도

$지니 불순도 = 1 - (양성 클래스 비율^2 + 음성 클래스 비율^2)$

• 분류 후에 얼마나 잘 분류했는지 평가하는 지표
• 지니 불순도가 낮을수록 순도가 높음
• 지니 불순도는 0~0.5 사이의 값(이진 분류의 경우)
  • 완벽하게 분류되면 : 0
  • 완벽하게 섞이면 (50:50) : 0.5
• 지니 불순도가 낮은 속성으로 의사 결정 트리 노드 결정

엔트로피

$엔트로피 = -음성클래스비율 \times log_2 (음성클래스비율) -양성클래스비율 \times log_2 (양성클래스비율)$

• 엔트로피는 0~1 사이의 값
  • 순수하게 분류되면 : 0
  • 완벽하게 섞이면 : 1

정보 이득 (Information Gain)

• 엔트로피는 단지 속성의 불순도를 표현
• 우리가 알고 싶은 것 = 어떤 속성이 얼마나 많은 정보를 제공하는가!

  $Gain(T,X) = Entropy(T) - Entropy(T,X)$

• 정보 이득이 크다 : 어떤 속성으로 분할할 때 불순도가 줄어든다
• 모든 속성에 대해 분할한 후 정보 이득 게산
• 정보 이득이 가장 큰 속성부터 분할

---

가지치기

• 가지치기를 하지 않으면 모델이 학습 데이터에는 매우 잘 맞지만, 평가 데이터에는 잘 맞지 않음 : 과대 적합, 일반화 되지 못함.
• 여러 하이퍼파라미터 값을 조정하여 가지치기를 할 수 있음
• 학습 데이터에 대한 성능은 떨어지나, 평가 데이터에 대한 성능을 높일 수 있음
• 가장 적절한 하이퍼파라미터 값을 찾도록 노력해야 함

주요 하이퍼파라미터

---

시각화

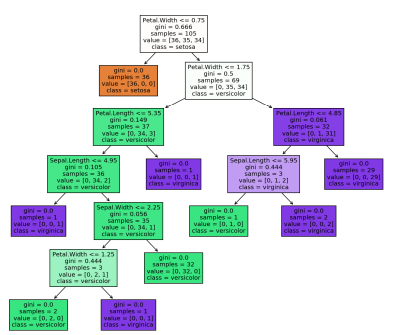
plot_tree로 시각화

• 적절한 figsize 설정 필요
• 불순도가 낮을 수록 진한 배경

# 시각화 모듈 불러오기
from sklearn.tree import plot_tree
fig = plt.figure(figsize=(12, 10))
plot_tree(model,
filled=True,
feature_names=list(x),
class_names=['setosa', 'versicolor', 'virginica'],
fontsize=10)
plt.show()

export_graphviz로 시각화

• 관련 라이브러리 설치 및 코딩 과정이 다소 복잡
• 좀 더 가독성 있는 시각화 가능

# 시각화 모듈 불러오기
from sklearn.tree import export_graphviz

# 이미지 파일 만들기
export_graphviz(model, # 모델 이름
filled=True,
feature_names=list(x),
class_names=['setosa', 'versicolor', 'virginica'], #임의값
rounded=True, #소수점
precision=3, #소수점
out_file='tree.dot')
!dot tree.dot -Tpng -otree.png -Gdpi=300

# 이미지 파일 로딩
from IPython.display import Image
Image(filename='tree.png', width=600)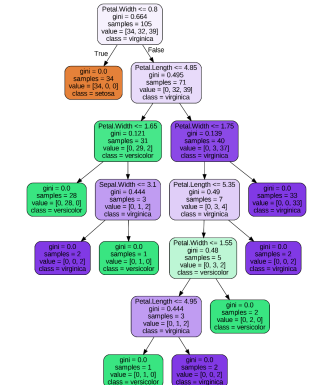 

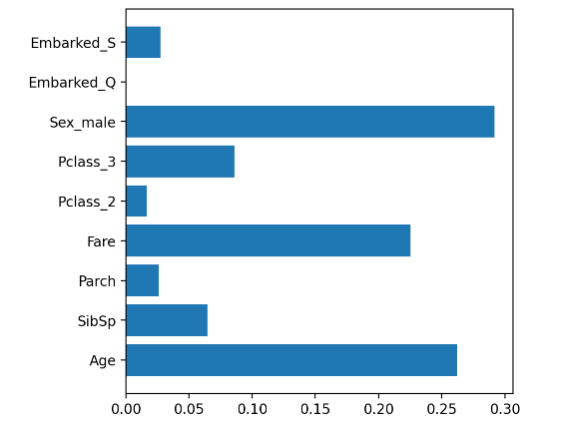
변수 중요도 시각화

• featureimportances속성 값으로 변수 중요도 확인
• Feature 순서대로 값을 가짐
• 값이 클 수록 Feature의 중요도가 높음

# 변수 중요도 시각화
plt.figure(figsize=(6, 8))
plt.barh(list(x), model.feature_importances_)
plt.ylabel('Features')
plt.xlabel('Importances')
plt.show()

---

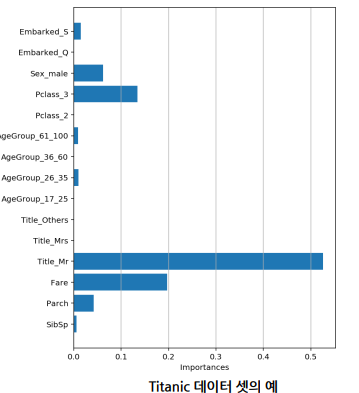
Decision Tree 실습 : Titanic

모델링

# 1단계: 불러오기
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import confusion_matrix, classification_report

# 2단계: 선언하기 (파라미터)
model = DecisionTreeClassifier(random_state=1,max_depth=5)

# 3단계: 학습하기
model.fit(x_train, y_train)

# 4단계: 예측하기
y_pred = model.predict(x_test)

# 5단계 평가하기
print(confusion_matrix(y_test,y_pred))
print(classification_report(y_test,y_pred))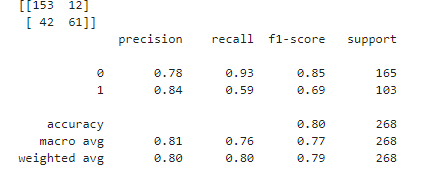

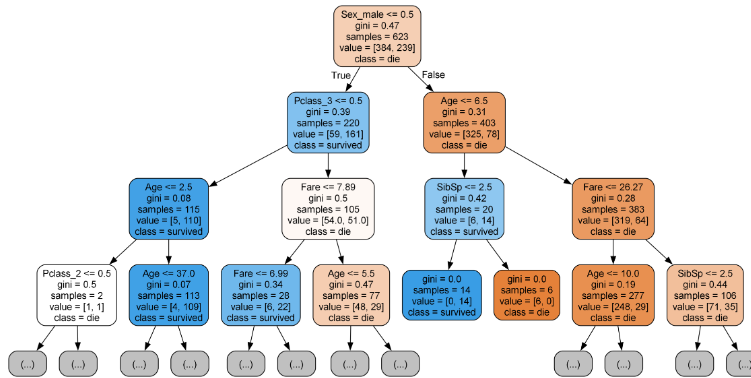
트리 시각화

# 시각화 모듈 불러오기
from sklearn.tree import export_graphviz
from IPython.display import Image

# 이미지 파일 만들기
export_graphviz(model,                                 # 모델 이름
                out_file='tree.dot',                   # 파일 이름
                feature_names=x.columns,               # Feature 이름
                class_names=['die', 'survived'],       # Target Class 이름
                rounded=True,                          # 둥근 테두리
                precision=2,                           # 불순도 소숫점 자리수
                filled=True,                           # 박스 내부 채우기
               max_depth=3                             # 보이는 depth
               )                          

# 파일 변환
!dot tree.dot -Tpng -otree.png -Gdpi=300

# 이미지 파일 표시
Image(filename='tree.png')

• 색상은 불순도의 농도에 따라 색깔이 다름
• 진하면 제대로 분류
  

변수 중요도 시각화

# 변수 중요도
plt.figure(figsize=(5, 5))
plt.barh(y=list(x), width=model.feature_importances_)
plt.show()